一、概述
在大规模机器学习中,需要应对巨大的训练数据及计算量。当单机遇到性能瓶颈时需要通过多台机器并行训练来弥补计算能力与内存的不足。采用并行方式进行机器学习时,常常分为模型并行与数据并行。模型并行是将模型拆分成多个分片,由几个计算节点分别持有,共同协作完成训练,适用于模型规模非常大的情形。数据并行是将数据拆分为不同的部分,分别存放在不同的计算节点上,同时每个计算节点都维护一个相同的模型。数据并行方式的训练过程中,每个计算节点只对自己存放的数据进行计算得到局部结果,然后再对局部结果进行全局归约。每个计算节点得到全局值之后,再进行模型更新。以下分别介绍并行计算中常用的归约算子,同时结合LightGBM的源码分析几个常用算子的实现方式。
二、并行计算中常用算子的主流实现方式剖析
在并行计算中,数值归约是非常重要且使用频率非常高的一种操作。数值归约算法实现方式的好坏直接影响整个计算过程的速度。常用的一些归约算子包括:Allreduce、Reduce、Allgather、Broadcast、ReduceScatter等。下面分别对这几种算子进行介绍。
一些定义:N-计算节点的总数; Ri - 第i个计算节点; Vi - 第i个计算节点的局部数值; root - 树状网络的根节点;k - 2k <= N的最大整数; remain = N - 2k; reducer - 归约操作;
2.1 Allgather
Allgather操作的目的是将计算节点的本地数据Vi同步到其他所有的计算节点,使得每一个节点都拥有一份V0 - VN-1的值。主流的实现方式有Recursive Doubling、Bruck Algorithm。
2.1.1 Recursive Doubling
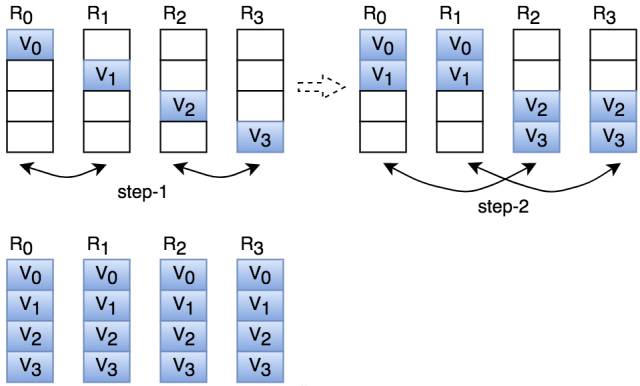
图1 Recursive Doubling算法的Allgather过程
上图描述了Recursive Doubling算法的工作过程。
第一步:在每一个节点上开辟sizeof(V0) + sizeof(V1) + sizeof(V2) + sizeof(V3)的内存,并且将本地的数据拷备到对应的起始位置;
第二步:如图所示,step-1时,节点与其相距20的节点进行数据互发;
第三步:step-2时,节点与其相距21的节点进行数据互发,发送的数据包括节点自身的数据以及之前接收的数据;
依此方式执行k步,最终所有的计算节点都拥有一份全局的数据了。
Recursive Doubling方式要求N为2的整数倍,计算节点收集到所有数据的通信次数为log(N)。
2.1.2 Bruck Algorithm
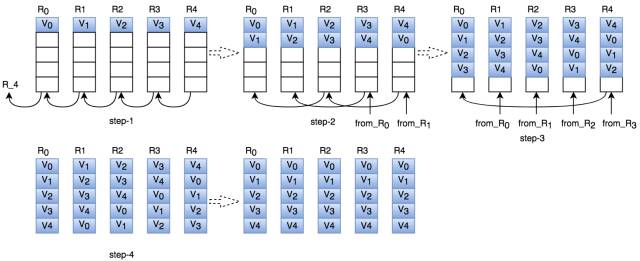
图2 Bruck 算法的Allgather过程
上图描述了Bruck Algorithm算法的工作过程。
第一步:如图,R1将数据发给R0, ......., R0将数据发给R4,发送一个数据块;
第二步:重复k步,第k步时,Ri将数据发送给Ri-2k,发送个数据块min(2k, N-sum_block);sum_block为计算节点上已有数据块大小。
第三步:调整数据块的顺序,调整方法在4.1节代码中介绍;
以上这种方式不要求N一定为2的整数倍,计算节点收集到所有数据的通信次数为ceil(log(N))。