紧接着上篇 二叉树的javascript实现 ,来说一下二叉树的遍历。
本次一本正经的胡说八道,以以下这个二叉树为例子进行遍历:
接着是要引入二叉树实现的代码:
|
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
|
function
Node(data, left, right) {
this
.data = data;
this
.left = left;
this
.right = right;
this
.show = show;
}
function
show() {
return
this
.data;
}
function
BST() {
this
.root =
null
;
this
.insert = insert;
}
function
insert(data) {
var
n =
new
Node(data,
null
,
null
);
if
(
this
.root ==
null
) {
this
.root = n;
}
else
{
var
current =
this
.root;
var
parent;
while
(
true
) {
parent = current;
if
(data < current.data) {
current = current.left;
if
(current ==
null
) {
parent.left = n;
break
;
}
}
else
{
current = current.right;
if
(current ==
null
) {
parent.right = n;
break
;
}
}
}
}
}
|
二叉树遍历的分类
二叉树的遍历分为先序、中序、后序遍历。这里说到的先序、中序、后序是相对于父节点来说。父节点的值先输出就是先序,三者间它在中间输出就是中序,最后输出就是后序。至于那个是父节点是相对而言的,因为除了叶子节点(最底下一层节点),其他每个节点都可以是父节点。
先序遍历
先序遍历就是,先打印父节点,然后是左子节点(左子树),然后再打印右子节点(子树)。
|
1
2
3
4
5
6
7
8
9
10
11
12
13
14
|
function
preOrder(node) {
if
(!(node ==
null
)) {
console.log(node.show() +
" "
);
preOrder(node.left);
preOrder(node.right);
}
}
// 给BST类添加先序遍历的成员方法
function
BST() {
this
.root =
null
;
this
.insert = insert;
this
.preOrder = preOrder;
}
|
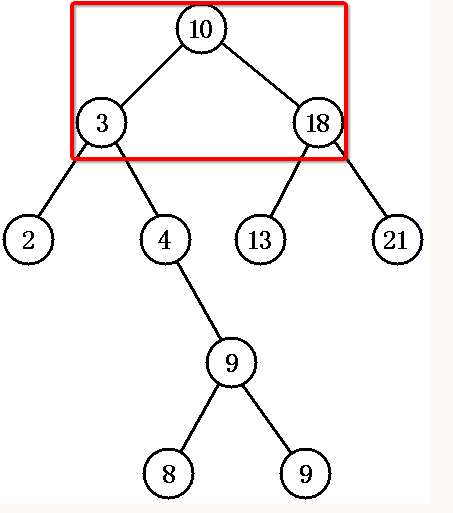
preOrder函数是递归实现的,应该说二叉树的遍历都是递归实现的。可能有些人会因为先序遍历的特征:“先打印父节点,然后是左子节点(左子树),然后再打印右子节点(子树)” 而陷入一个错误的想法,这想法是什么请看下图:
注意红框部分,父节点是10,左子节点是3,右子节点是18,因为上面的结论,可能会错误地认为打印的顺序是10 → 3 → 18,然而事实并非如此[捂脸],真是的顺序是:先打印10,然后是打印左子树,打印完左子树的全部节点后,才开始打印以10位父节点的右子树:
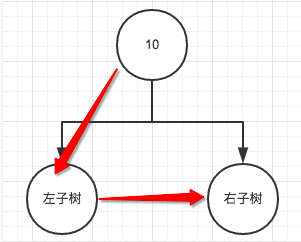
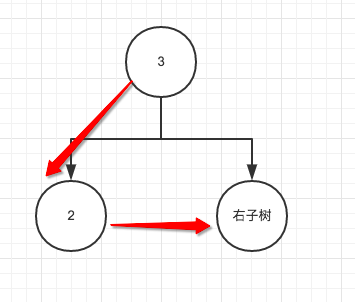
这个时候,你的脑海就该这样想:
然后是这样想:
如此类推打印完以10为父节点的左子树,然后也是以这样的方式打印以10为父节点的右子树,按着这种 拆分代替的思想 来理解会更好明白二叉树的遍历。
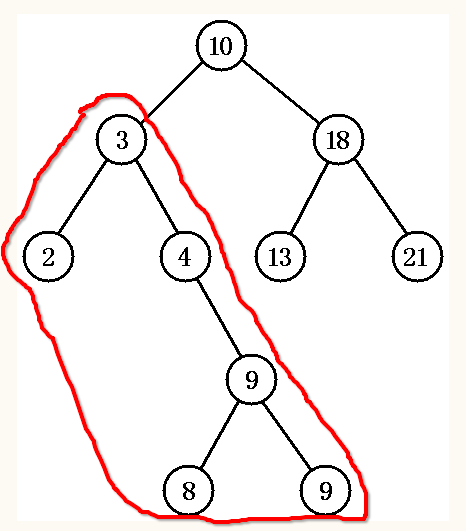
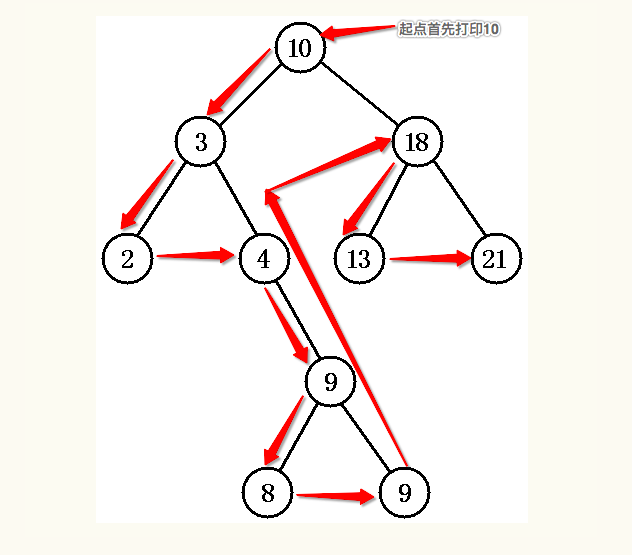
然后最终,先序遍历改二叉树的顺序是:
按图的输出顺序是:10 -> 3 -> 2 -> 4 -> 9 -> 8 -> 9 -> 18 -> 13 -> 21
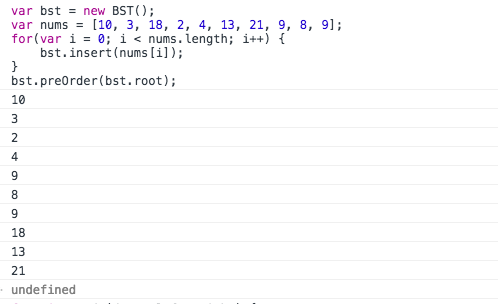
最后来实践一下,先序遍历:
|
1
2
3
4
5
6
|
var
bst =
new
BST();
var
nums = [10, 3, 18, 2, 4, 13, 21, 9, 8, 9];
for
(
var
i = 0; i < nums.length; i++) {
bst.insert(nums[i]);
}
bst.preOrder(bst.root);
|
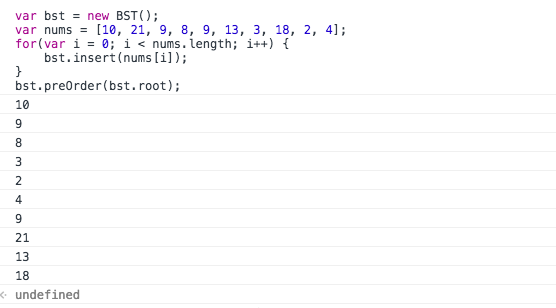
这里强调一下,输出顺序和插入顺序有关的,因为你插入顺序不同生成的二叉树也是不同的。有疑问的可以去 二叉树的javascript实现 细看一下,有比较明白的说明了二叉树,也可以实验一下:
中序遍历
看完先序遍历,已经可以类推到很多和中序、后序遍历相关的知识点。中序遍历的特征是:先打印左子树(左子节点),接着打印父节点,最后打印右子树(右子节点)。
|
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
|
function
inOrder(node) {
if
(!(node ==
null
)) {
inOrder(node.left);
console.log(node.show() +
" "
);
inOrder(node.right);
}
}
// 给BST类添加该成员方法
function
BST() {
this
.root =
null
;
this
.insert = insert;
this
.preOrder = preOrder;
this
.inOrder = inOrder;
}
|
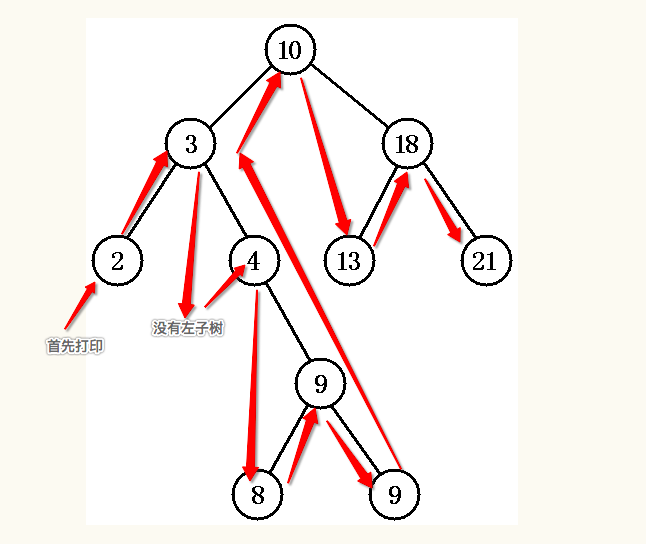
中序遍历的打印顺序:
按上图的输出顺序是:2 -> 3 -> 4 -> 8 -> 9 -> 9 -> 10 -> 13 -> 18 -> 21
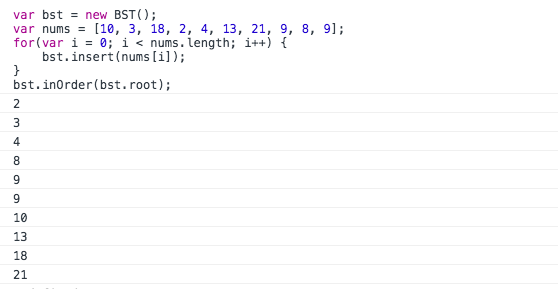
接着是,实践一下中序遍历:
后序遍历
|
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
|
function
postOrder(node) {
if
(!(node ==
null
)) {
postOrder(node.left);
postOrder(node.right);
console.log(node.show() +
" "
);
}
}
// 给BST类添加该成员方法
function
BST() {
this
.root =
null
;
this
.insert = insert;
this
.preOrder = preOrder;
this
.inOrder = inOrder;
this
.postOrder = postOrder;
}
|
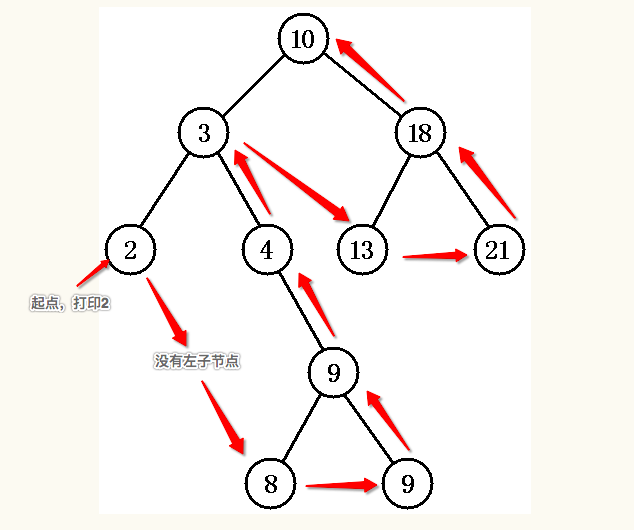
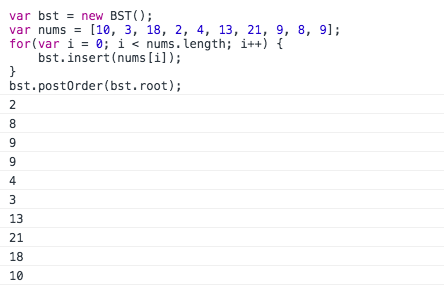
后序遍历的打印顺序
按上图的输出顺序是:2 -> 8 -> 9 -> 9 -> 4 -> 3 -> 13 -> 21 -> 18 -> 10
以上就是本文的全部内容,希望对大家的学习有所帮助,也希望大家多多支持脚本之家。
原文链接:http://www.jianshu.com/p/72ea83e2feab#