动手学深度学习4.3 多层感知机的简洁实现-笔记&练习（PyTorch）

以下内容为结合李沐老师的课程和教材补充的学习笔记，以及对课后练习的一些思考，自留回顾，也供同学之人交流参考。

本节课程地址：10 多层感知机 + 代码实现 - 动手学深度学习v2_哔哩哔哩_bilibili

本节教材地址：4.3. 多层感知机的简洁实现 — 动手学深度学习 2.0.0 documentation (d2l.ai)

本节开源代码：...>d2l-zh>pytorch>chapter_multilayer-perceptrons>mlp-concise.ipynb

多层感知机的简洁实现

本节将介绍(通过高级API更简洁地实现多层感知机)。

import torch
from torch import nn
from d2l import torch as d2l

模型

与softmax回归的简洁实现（ 3.7节）相比，唯一的区别是我们添加了2个全连接层（之前我们只添加了1个全连接层）。第一层是[隐藏层]，它(包含256个隐藏单元，并使用了ReLU激活函数)。第二层是输出层。

net = nn.Sequential(nn.Flatten(),
                    nn.Linear(784, 256),
                    nn.ReLU(),
                    nn.Linear(256, 10))

def init_weights(m):
    if type(m) == nn.Linear:
        nn.init.normal_(m.weight, std=0.01)

net.apply(init_weights);

[训练过程]的实现与我们实现softmax回归时完全相同，这种模块化设计使我们能够将与模型架构有关的内容独立出来。

batch_size, lr, num_epochs = 256, 0.1, 10
loss = nn.CrossEntropyLoss(reduction='none')
trainer = torch.optim.SGD(net.parameters(), lr=lr)
train_iter, test_iter = d2l.load_data_fashion_mnist(batch_size)
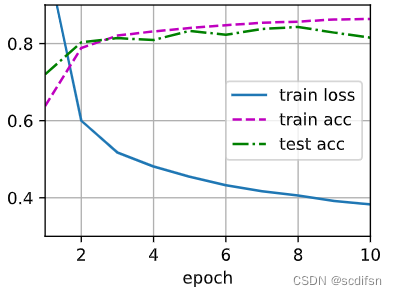
d2l.train_ch3(net, train_iter, test_iter, loss, num_epochs, trainer)

小结

我们可以使用高级API更简洁地实现多层感知机。
对于相同的分类问题，多层感知机的实现与softmax回归的实现相同，只是多层感知机的实现里增加了带有激活函数的隐藏层。

练习

尝试添加不同数量的隐藏层（也可以修改学习率），怎么样设置效果最好？

解：实现过程与mlp-scratch的练习2和3基本一致，用API简化代码，如下：

import torch
from torch import nn 
from d2l import torch as d2l
import matplotlib.pyplot as plt
import itertools

#设置固定参数
batch_size, num_epochs = 256, 10

# 定义可变超参数
hidden_layers = [1, 2, 4]  
lrs = [0.01, 0.1, 1]

accuracies = []
hyperparameters = []

best_accuracy = 0
best_hyperparameters = {}
best_iteration = 0

# 使用嵌套循环遍历所有超参数组合
for i, (lr, layers) in enumerate(itertools.product(lrs, hidden_layers)):
    net = nn.Sequential(nn.Flatten(),
                        nn.Linear(784, 256),
                        nn.ReLU())

    for _ in range(layers):
        net.add_module('hidden_linear', nn.Linear(256, 256))
        net.add_module('hidden_relu', nn.ReLU())

    net.add_module('output_linear', nn.Linear(256, 10))

    def init_weights(m):
        if type(m) == nn.Linear:
            nn.init.normal_(m.weight, std=0.01)

    net.apply(init_weights)

    loss = nn.CrossEntropyLoss(reduction='none')

    trainer = torch.optim.SGD(net.parameters(), lr=lr)

    train_iter, test_iter = d2l.load_data_fashion_mnist(batch_size)

    for epoch in range(num_epochs):

        d2l.train_epoch_ch3(net, train_iter, loss, trainer)

    accuracy = d2l.evaluate_accuracy(net, test_iter)
    accuracies.append(accuracy)
    hyperparameters.append({'learning_rate': lr,
                            'hidden_layers': layers})

    # 更新最佳结果
    if accuracy > best_accuracy:
        best_accuracy = accuracy
        best_hyperparameters = {'learning_rate': lr,
                                'hidden_layers': layers}
        best_iteration = i

# 绘制准确性图表
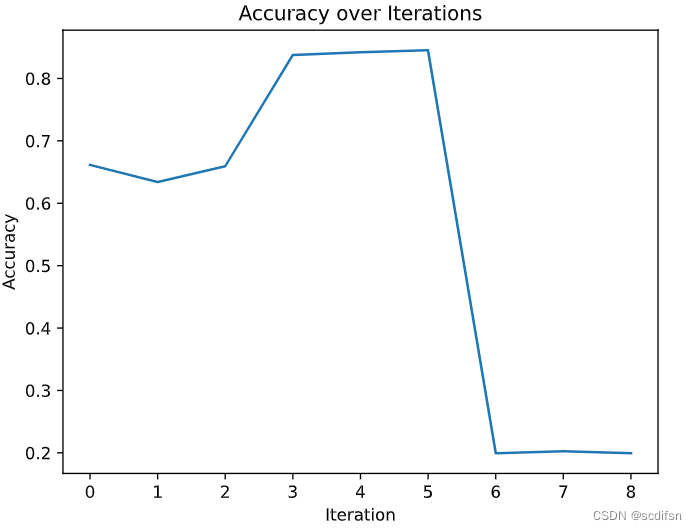
plt.plot(range(len(accuracies)), accuracies)
plt.xlabel('Iteration')
plt.ylabel('Accuracy')
plt.title('Accuracy over Iterations')
plt.show()

print("Best iteration:", best_iteration)
print("Best hyperparameters:", best_hyperparameters)
print("Best accuracy:", best_accuracy)

输出结果：

Best iteration: 5
Best hyperparameters: {'learning_rate': 0.1, 'hidden_layers': 4}
Best accuracy: 0.8451

2. 尝试不同的激活函数，哪个效果最好？

解：效果最好的是ReLU()，代码如下：

import torch
from torch import nn
from d2l import torch as d2l

batch_size, lr, num_epochs = 256, 0.1, 10

train_iter, test_iter = d2l.load_data_fashion_mnist(batch_size)

#设置激活函数合集
activation_functions = [nn.ReLU(), nn.Sigmoid(), nn.Tanh()]

accuracies = []
best_accuracy = 0
best_activation_function_number = 0

#设置循环更换不同的激活函数
for i in range(3):
    net = nn.Sequential(nn.Flatten(),
                        nn.Linear(784, 256),
                        activation_functions[i],
                        nn.Linear(256, 10))
    net.apply(init_weights)

    loss = nn.CrossEntropyLoss(reduction='none')
    trainer = torch.optim.SGD(net.parameters(), lr=lr)

    for epoch in range(num_epochs):

        d2l.train_epoch_ch3(net, train_iter, loss, trainer)

    accuracy = d2l.evaluate_accuracy(net, test_iter)
    accuracies.append(accuracy)

    # 更新最佳结果
    if accuracy > best_accuracy:
        best_accuracy = accuracy
        best_activation_function_number = i

# 绘制准确性图表
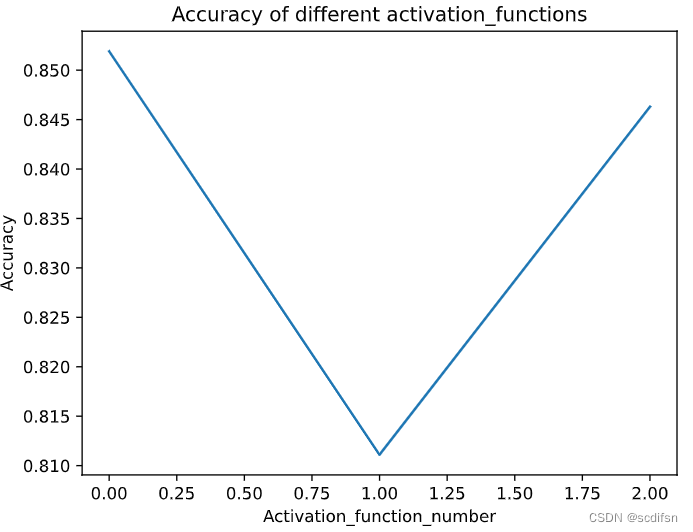
plt.plot(range(len(accuracies)), accuracies)
plt.xlabel('Activation_function_number')
plt.ylabel('Accuracy')
plt.title('Accuracy of different activation_functions')
plt.show()

print("Best activation_function:", activation_functions[best_activation_function_number])
print("Best accuracy:", best_accuracy)

输出结果：

Best activation_function: ReLU()
Best accuracy: 0.8519

3. 尝试不同的方案来初始化权重，什么方法效果最好？

解：常用的权重初始化方法如下：
· 均匀分布初始化：将权重从均匀分布中随机采样。例如，使用nn.init.uniform_()初始化权重。
· 正态分布初始化：将权重从正态分布中随机采样。例如，使用nn.init.normal_()初始化权重。
· Xavier初始化：根据每个网络层的输入和输出通道数量，通过一个经验公式来设置权重的初始尺度。可以使用nn.init.xavier_uniform_()或nn.init.xavier_normal_()来实现。
· He初始化：类似于Xavier初始化，但是使用了不同的尺度系数，特别适用于ReLU激活函数。可以使用nn.init.kaiming_uniform_()或nn.init.kaiming_normal_()来实现。
比较如下：

def init_weights(init_method):
    def _init_weights(m):
        if type(m) == nn.Linear:
            init_method(m.weight)
    return _init_weights
import torch
from torch import nn
from d2l import torch as d2l

batch_size, lr, num_epochs = 256, 0.1, 10

train_iter, test_iter = d2l.load_data_fashion_mnist(batch_size)

#设置权重初始化方法合集
init_weights_methods = [nn.init.uniform_, 
                        nn.init.uniform_, 
                        nn.init.xavier_normal_, 
                        nn.init.xavier_uniform_, 
                        nn.init.kaiming_normal_, 
                        nn.init.kaiming_uniform_]

accuracies = []
best_accuracy = 0
best_init_weights_methods_number = 0

#设置循环更换不同的激活函数
for i in range(6):

    net = nn.Sequential(nn.Flatten(),
                        nn.Linear(784, 256),
                        nn.ReLU(),
                        nn.Linear(256, 10))
    net.apply(init_weights(init_weights_methods[i]))

    loss = nn.CrossEntropyLoss(reduction='none')
    trainer = torch.optim.SGD(net.parameters(), lr=lr)

    for epoch in range(num_epochs):

        d2l.train_epoch_ch3(net, train_iter, loss, trainer)

    accuracy = d2l.evaluate_accuracy(net, test_iter)
    accuracies.append(accuracy)

    # 更新最佳结果
    if accuracy > best_accuracy:
        best_accuracy = accuracy
        best_init_weights_methods_number = i

# 绘制准确性图表
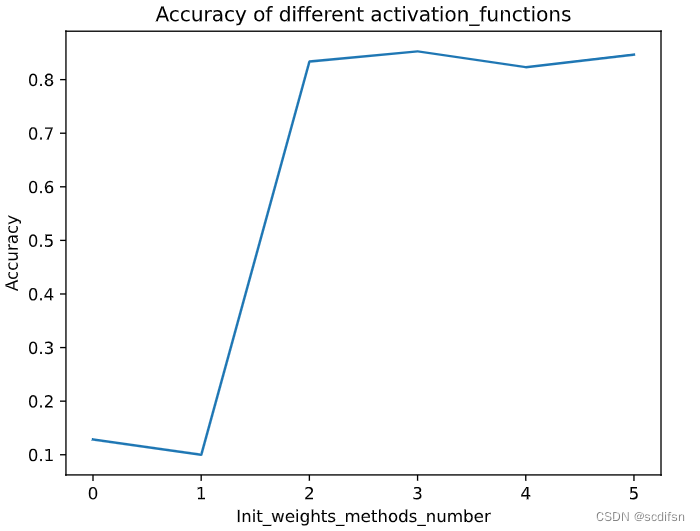
plt.plot(range(len(accuracies)), accuracies)
plt.xlabel('Init_weights_methods_number')
plt.ylabel('Accuracy')
plt.title('Accuracy of different activation_functions')
plt.show()

print("Best init_weights_method:", init_weights_methods[best_init_weights_methods_number])
print("Best accuracy:", best_accuracy)

输出结果：

Best activation_function: ReLU()
Best accuracy: 0.8519