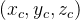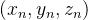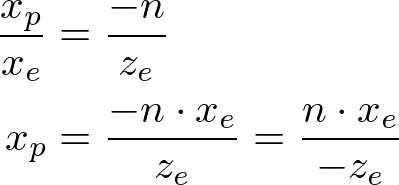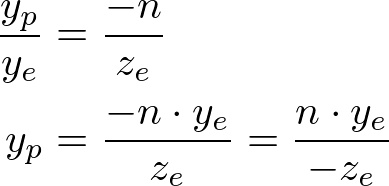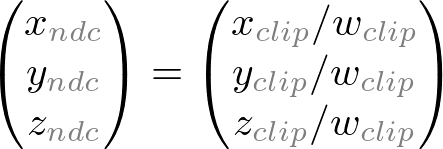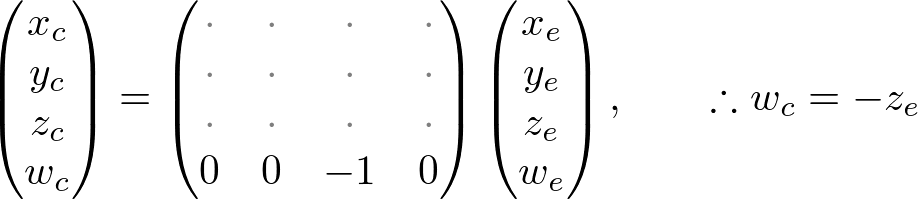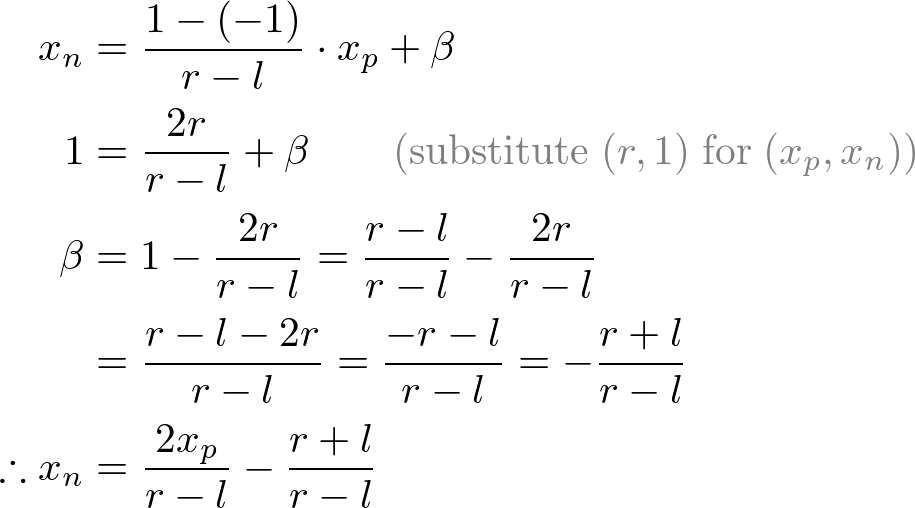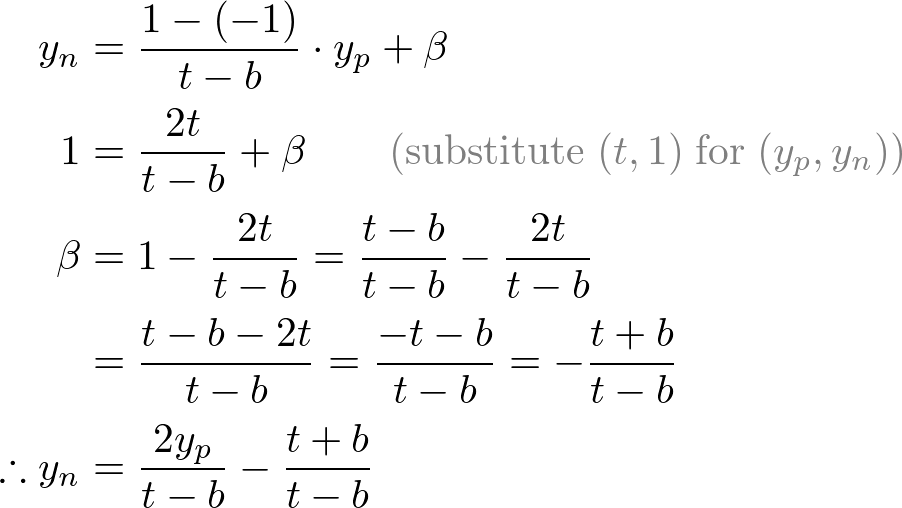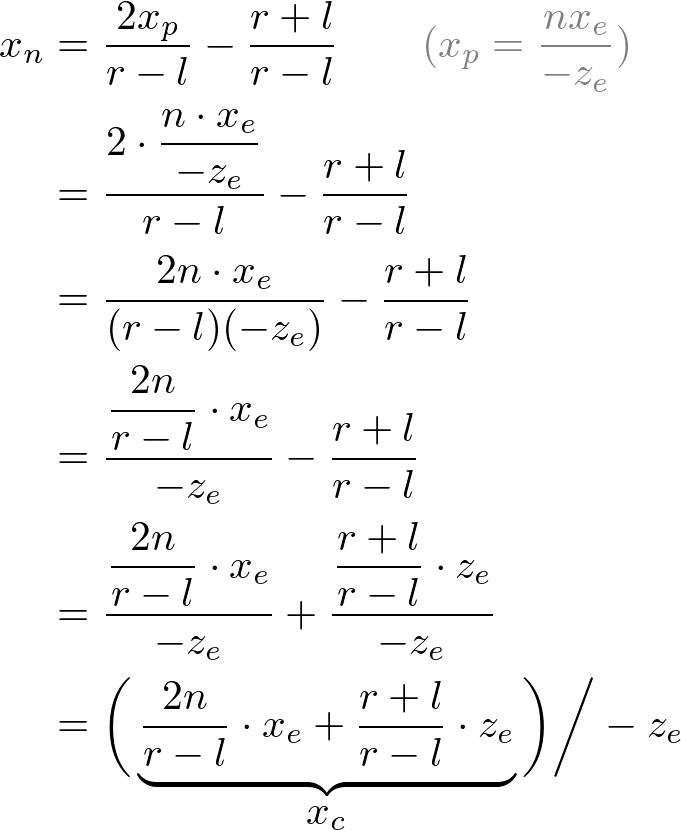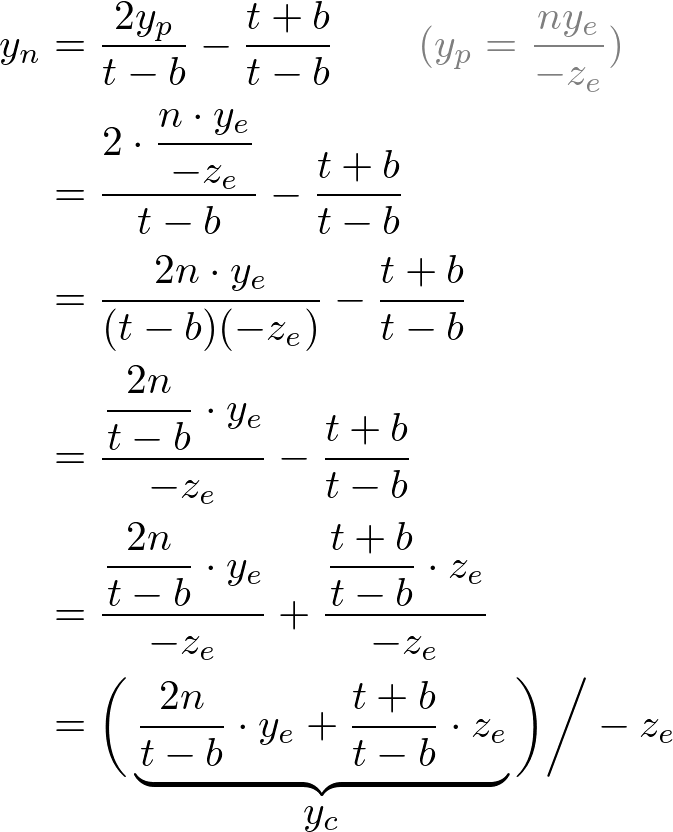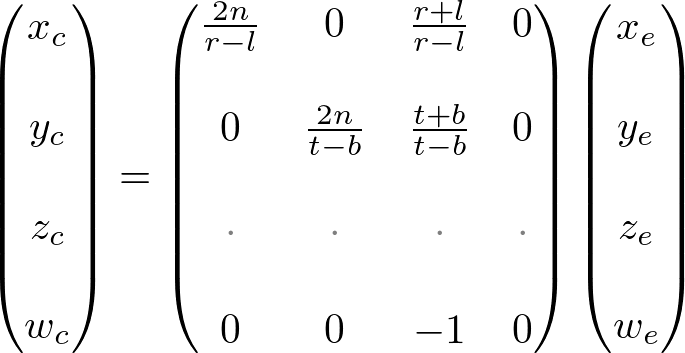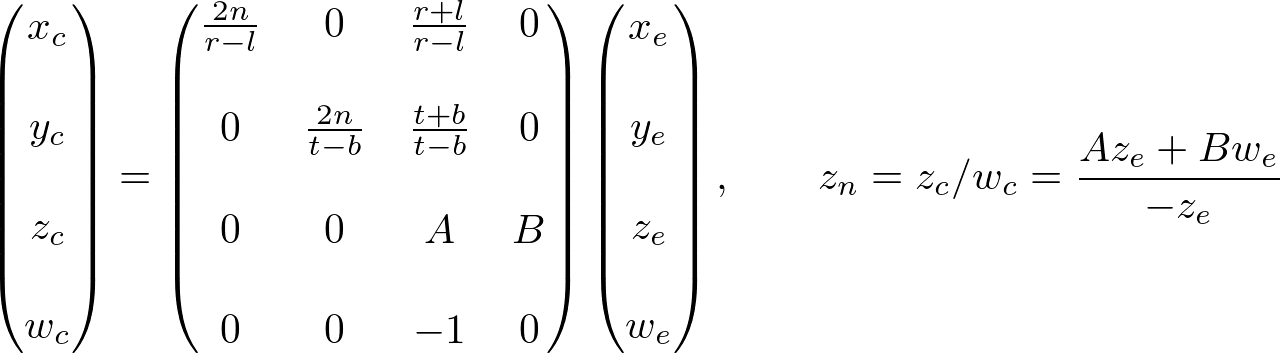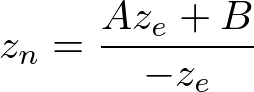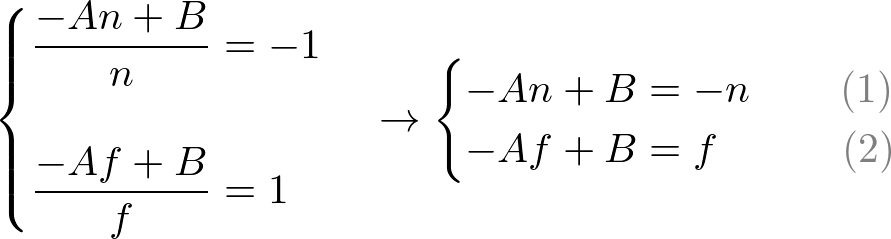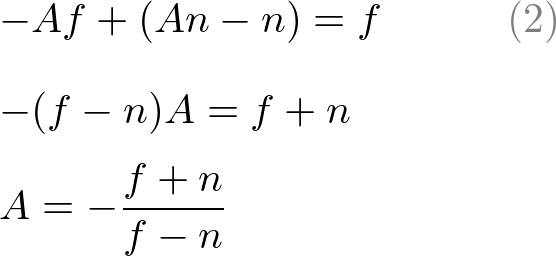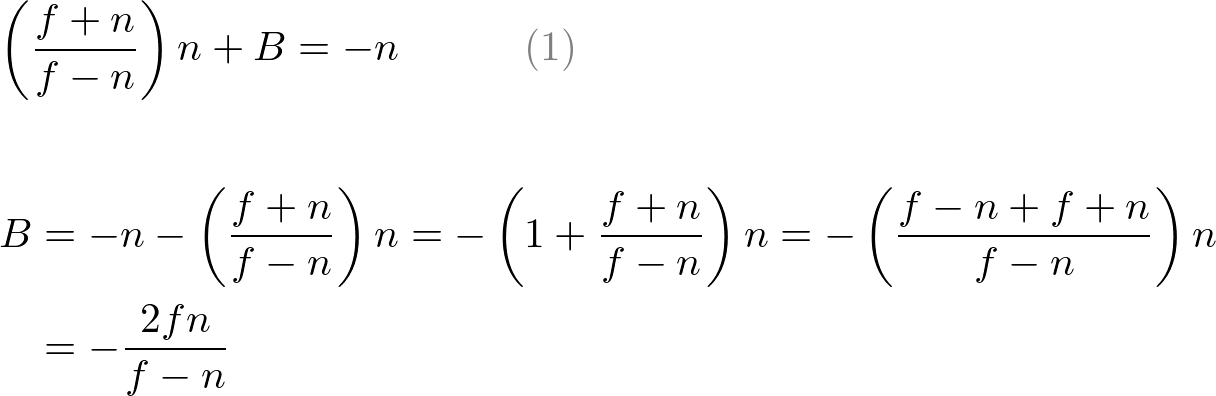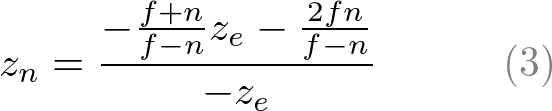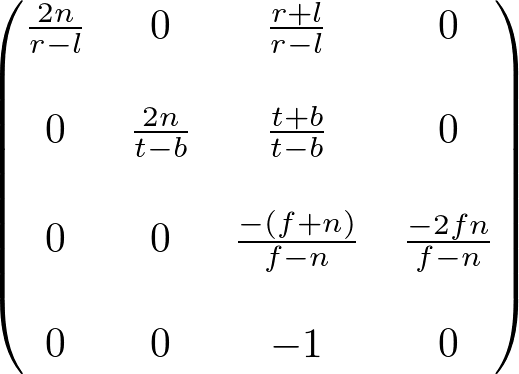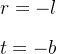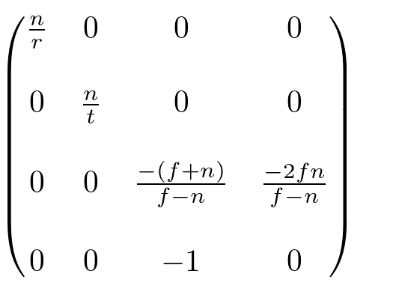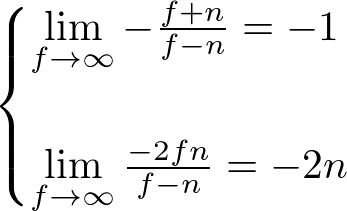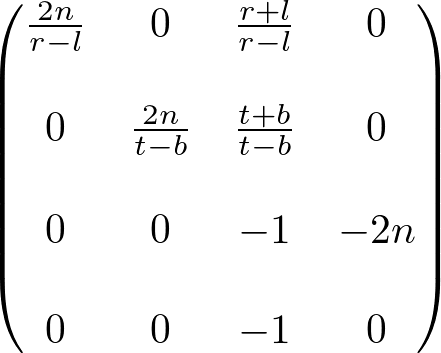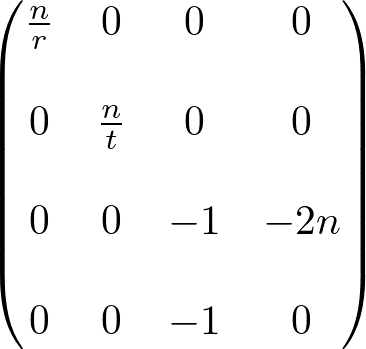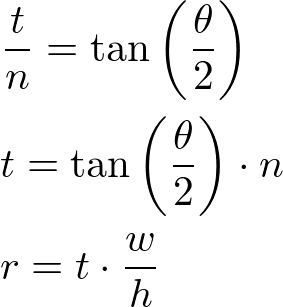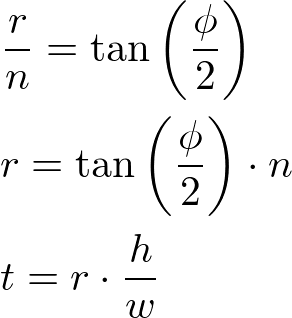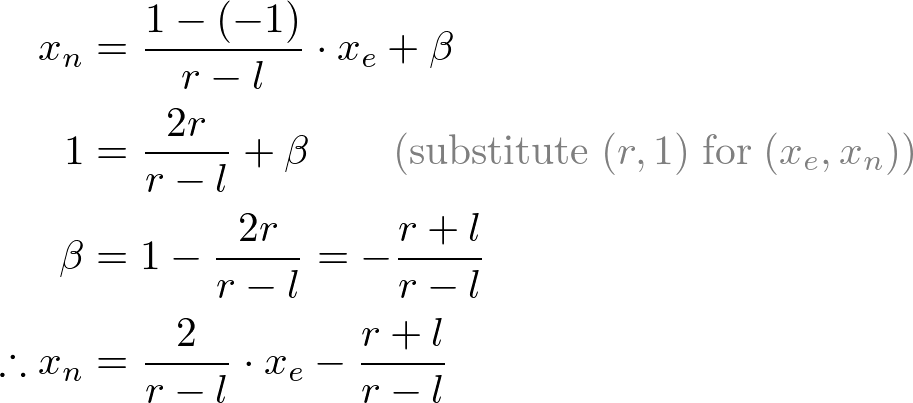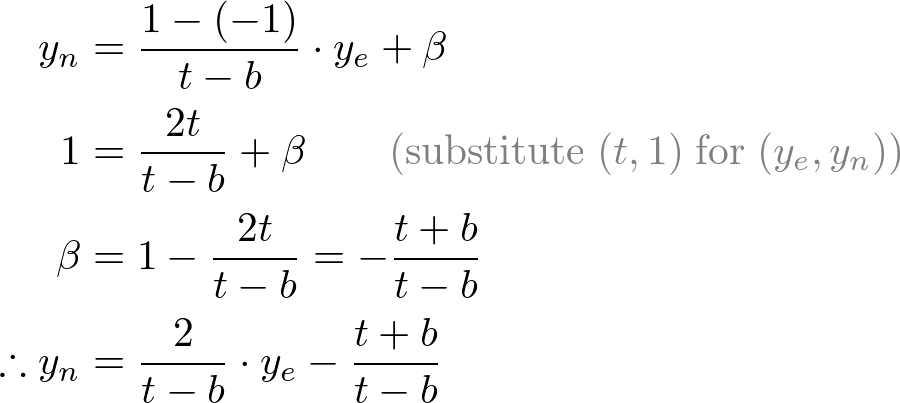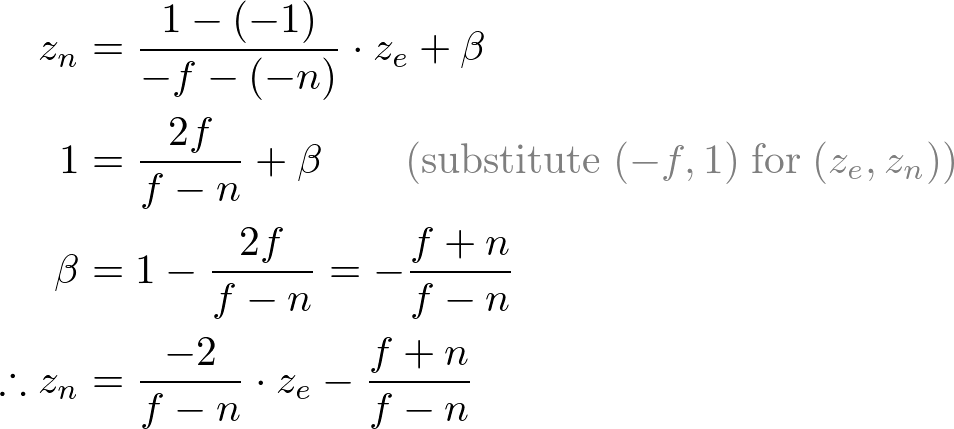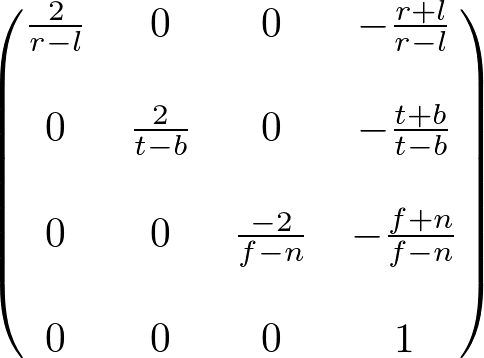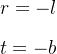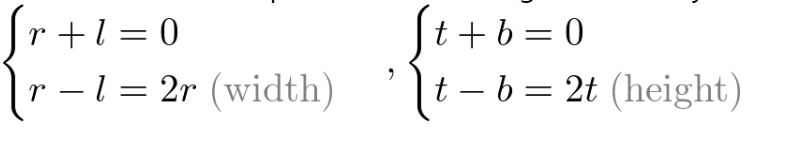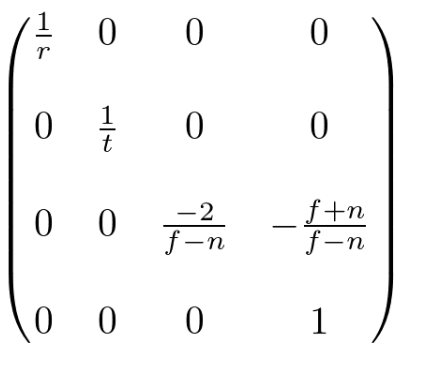1.概述
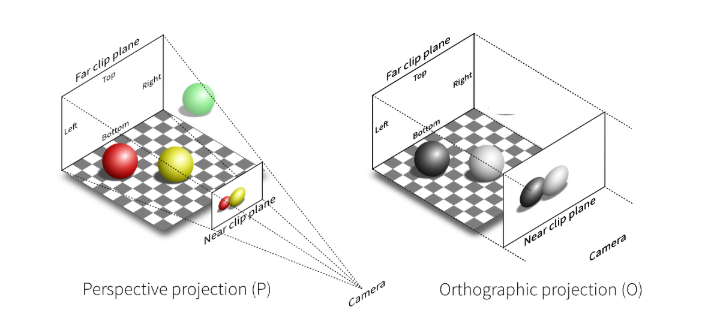
计算机显示器是一个2D表面。由OpenGL渲染的3D场景必须被投影到计算机屏幕上作为2D图像。GL_PROJECTION矩阵用于这种投影变换。首先,它将所有顶点数据从eye坐标系(也可以称为相机坐标系,即由谁来观看)转换到裁剪坐标系(clip coordinate)。然后,这些裁剪坐标通过除以clip坐标的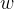
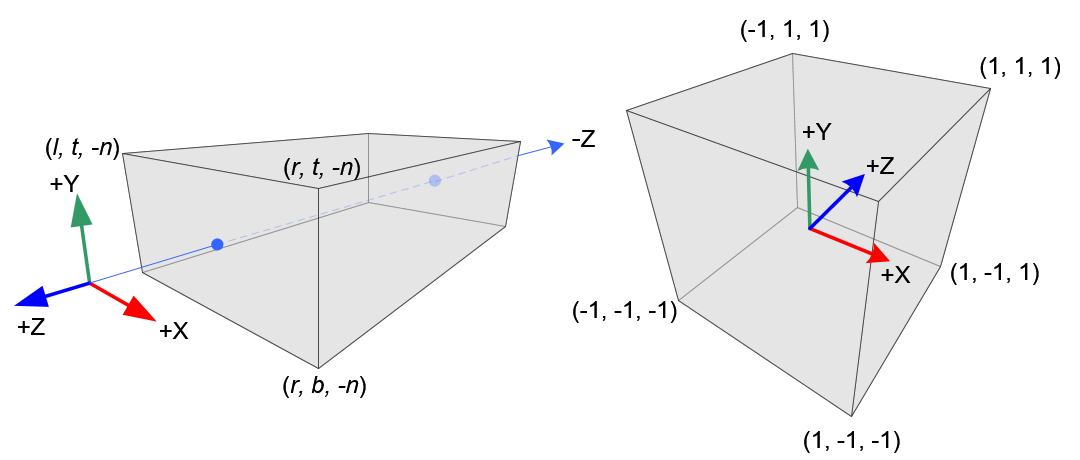
因此,我们必须记住,裁剪的视锥体和NDC变换都集成在GL_PROJECTION矩阵中。以下部分描述了如何从6个参数:left、right、bottom、top、near和far边界值,来构建投影矩阵。
需要注意,视锥体的裁剪是在clip坐标中执行的,先于除以
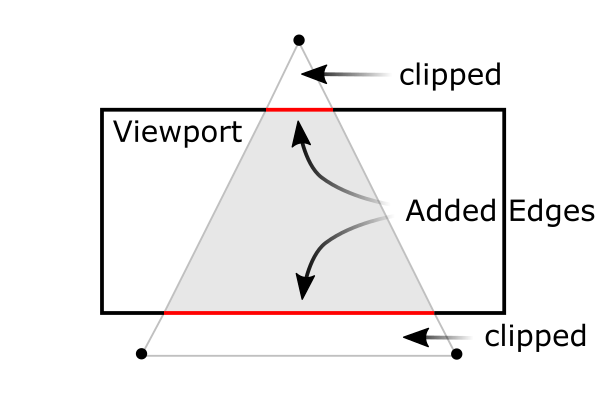
OpenGL会在发生裁剪的地方生成新的边,如下图1,一个三角形经裁后,成了一个梯形,两条红色的边就是裁剪后新生成的。
图1. 一个被视口裁剪的三角形
2.透视投影
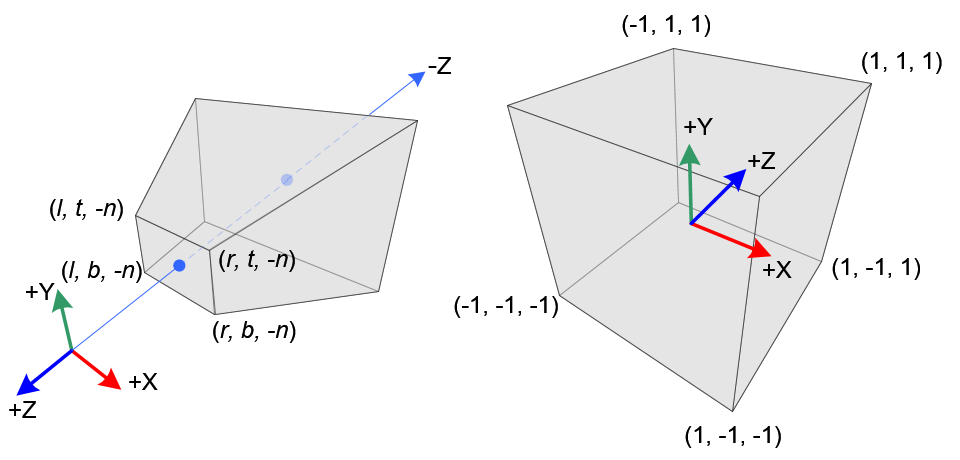
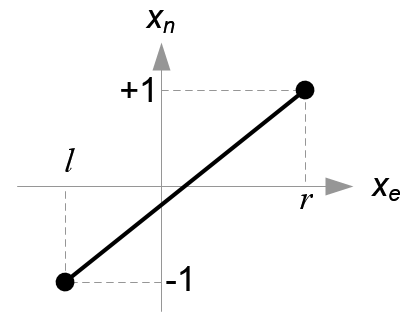
图2. 透视截断视锥体和归一化设备坐标(NDC)示意图
一共涉及到6个坐标边界:
n表示near,对应为视锥体近面z坐标,f表示far,对应为远面z坐标,
t表示视锥体top面z坐标,b表示 bottom面y坐标,
r表示视锥体right x坐标,left表示左面x坐标。一共涉及到3个坐标系:
eye坐标系(也称为view坐标系,或者相机坐标系),
clip坐标系,
NDC坐标系,
在透视投影中,截断的视锥体(相机坐标)中的3D点被映射到立方体(NDC);x坐标的范围从![[l,r]](/image/aHR0cHM6Ly9sYXRleC5jc2RuLm5ldC9lcT8lNUJsJTJDciU1RA%3D%3D)
![[-1,1]](/image/aHR0cHM6Ly9sYXRleC5jc2RuLm5ldC9lcT8lNUItMSUyQzElNUQ%3D)
![[b,t]](/image/aHR0cHM6Ly9sYXRleC5jc2RuLm5ldC9lcT8lNUJiJTJDdCU1RA%3D%3D)
![[-1,1]](/image/aHR0cHM6Ly9sYXRleC5jc2RuLm5ldC9lcT8lNUItMSUyQzElNUQ%3D)
![[-n,-f]](/image/aHR0cHM6Ly9sYXRleC5jc2RuLm5ldC9lcT8lNUItbiUyQy1mJTVE)
![[-1,1]](/image/aHR0cHM6Ly9sYXRleC5jc2RuLm5ldC9lcT8lNUItMSUyQzElNUQ%3D)
需要注意,眼坐标是在右手坐标系中定义的,但NDC使用左手坐标系。也就是说,在眼空间中,相机位于原点,看向-Z轴,但在NDC中,它是看向+Z轴。由于glFrustum()接受的的near和far是始终为正,我们在构建GL_PROJECTION矩阵期间需要对它们取反。
在OpenGL中,眼空间中的3D点被投影到近裁剪平面(投影平面)。以下图表显示了如何在近平面上将眼空间中的点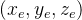
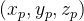
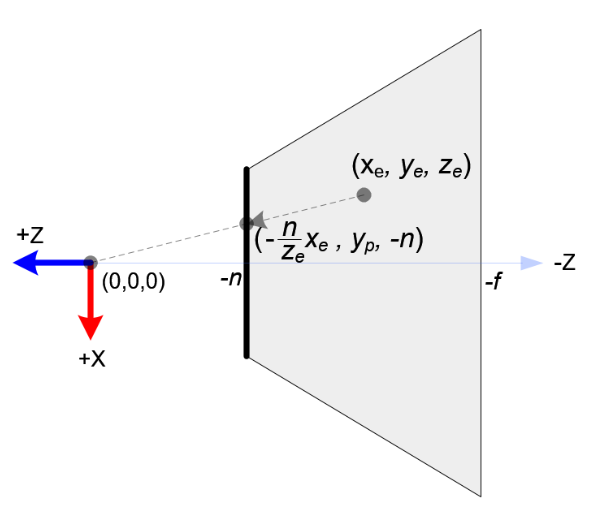
图3. 视景体中的俯视图
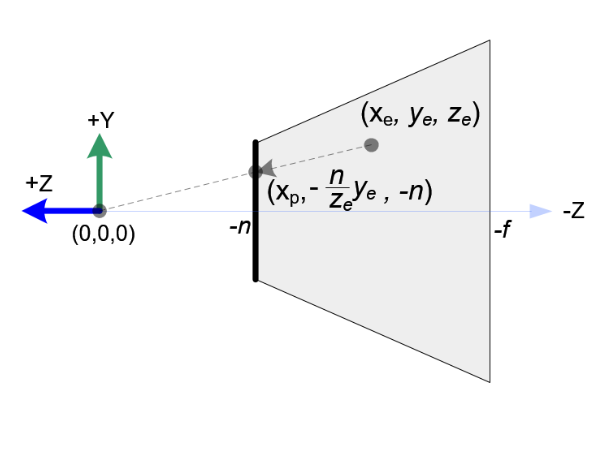
图4. 视景体中的侧视图
从截断锥体的俯视图看,眼空间中的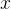


从截锥体的侧视图看,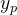
请注意,
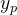
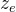
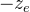
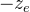
,
因此,我们可以将裁剪坐标的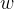
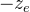
进一步,将
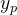

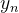
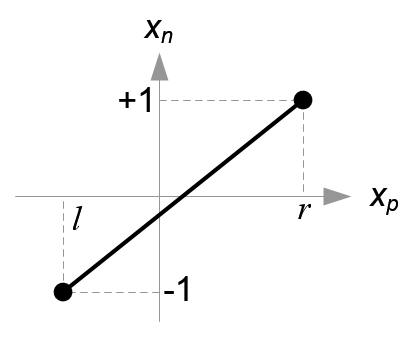
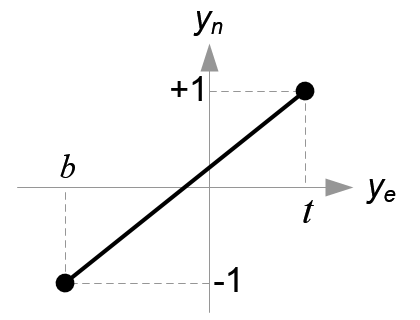
![[l,r]\Rightarrow [-1,1]](/image/aHR0cHM6Ly9sYXRleC5jc2RuLm5ldC9lcT8lNUJsJTJDciU1RA%3D%3D%5CRightarrow%20%5B-1%2C1%5D)
![[b,t]\Rightarrow [-1,1]](/image/aHR0cHM6Ly9sYXRleC5jc2RuLm5ldC9lcT8lNUJiJTJDdCU1RA%3D%3D%5CRightarrow%20%5B-1%2C1%5D)
图5.把xp映射到xn
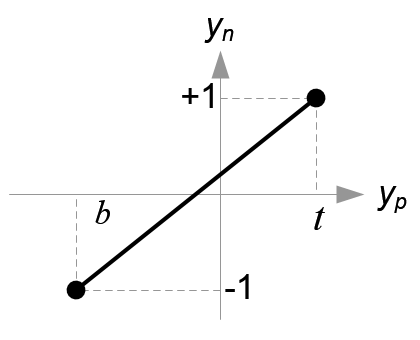
同理,可以求出 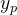
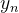
图6.把yp映射到yn
然后,在上式中代入
请注意,上面刚刚求得的


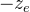
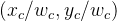

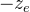

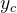
根据这些方程,我们可以找到GL_PROJECTION矩阵的第一行和第二行。
现在,我们只需要求解GL_PROJECTION矩阵的第三行。找到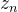
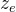
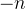
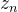
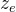
在eye空间中,
为了找到系数 A和 B,我们把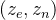
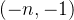
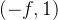
上述方程(1)改写为:
将方程(1')代入方程2)中的 B,然后求解A:
将A代入eq.(1)以得到B;
由此,我们得到了A和B。因此,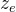
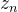
最后,完整的透视投影矩阵GL_PROJECTION:
上面这是一个通用视景体的投影矩阵。当视景体是对称时,即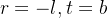
也就是如下形式:
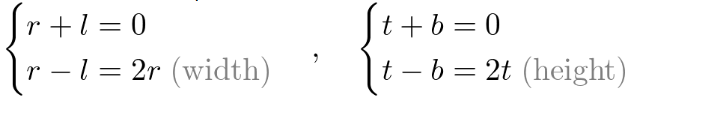
透视投影矩阵们已经求出来了,在继续往下探讨之前,可以再看一下上面的方程(3),即:
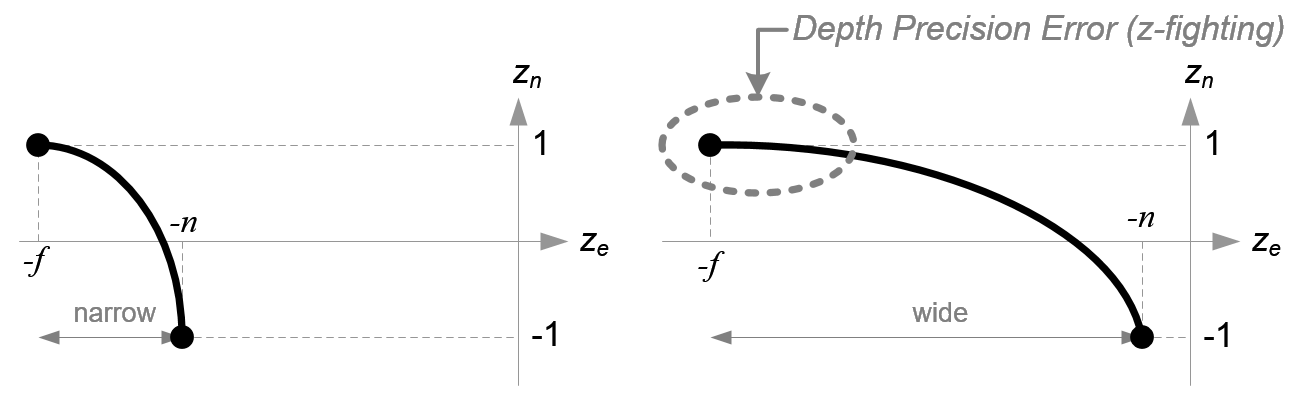
可以看到它是一个有理函数(rational function),且是一个非线性函数。这意味着在近裁剪平面(near plane)附近,它具有很高的精度(very high precision),而在远裁剪面(far plane)附近具有非常小的精度(very little precision)。如果![[-n,-f]](/image/aHR0cHM6Ly9sYXRleC5jc2RuLm5ldC9lcT8lNUItbiUyQy1mJTVE)
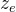
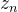
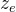
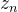
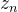
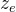
图7.深度缓存的精度对比
3.无穷透视投影矩阵
对于透视投影矩阵,如果设置矩阵第三行远裁剪平面在无穷远处,即,可以简化为:
因此,对于通用和对称透视投影矩阵,在无穷远裁剪平面,则有:
通用无穷透视投影矩阵
对称无穷透视投影矩阵
需要注意,无穷投影矩阵仍然受到深度精度的影响。
4.带视场的透视投影矩阵
对于特定窗口尺寸上的透视投影,很难用给定的近平面和远平面正确确定4个参数(左、右、上、下)。可以从垂直/水平视场角和纵横比、宽度/高度轻松导出这4个参数。然而,这些转换仅限于对称透视投影矩阵。
4.1 使用垂直FOV
如果垂直视场为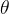
图8.使用垂直FOV的透视投影矩阵
// This creates a symmetric frustum with vertical FOV
// by converting 4 params (fovy, aspect=w/h, near, far)
// to 6 params (l, r, b, t, n, f)
Matrix4 makeFrustum(float fovY, float aspectRatio, float front, float back)
{
const float DEG2RAD = acos(-1.0f) / 180;
float tangent = tan(fovY/2 * DEG2RAD); // tangent of half fovY
float top = front * tangent; // half height of near plane
float right = top * aspectRatio; // half width of near plane
// params: left, right, bottom, top, near(front), far(back)
Matrix4 matrix;
matrix[0] = front / right;
matrix[5] = front / top;
matrix[10] = -(back + front) / (back - front);
matrix[11] = -1;
matrix[14] = -(2 * back * front) / (back - front);
matrix[15] = 0;
return matrix;
}
4.2 使用水平 FOV
图9.使用水平FOV的透视投影矩阵
首先,用半个水平视场角的切线计算半宽度(右)。然后,使用屏幕宽度和高度的纵横比计算半个高度(顶部)
// This creates a symmetric frustum with horizontal FOV
// by converting 4 params (fovx, aspect=w/h, near, far)
// to 6 params (l, r, b, t, n, f)
Matrix4 makeFrustum(float fovX, float aspectRatio, float front, float back)
{
const float DEG2RAD = acos(-1.0f) / 180;
float tangent = tan(fovX/2 * DEG2RAD); // tangent of half fovX
float right = front * tangent; // half width of near plane
float top = right / aspectRatio; // half height of near plane
// params: left, right, bottom, top, near(front), far(back)
Matrix4 matrix;
matrix[0] = front / right;
matrix[5] = front / top;
matrix[10] = -(back + front) / (back - front);
matrix[11] = -1;
matrix[14] = -(2 * back * front) / (back - front);
matrix[15] = 0;
return matrix;
}
5.正交投影
构建正交投影矩阵相对来说会简单一些。
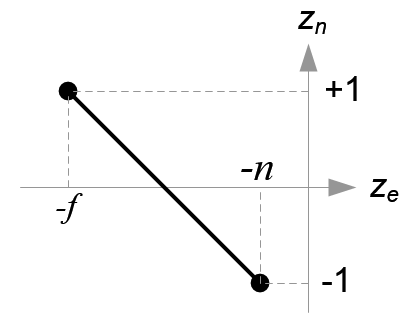
图8. 正交投影视景体及对应的NDC
eye空间中的所有
把
把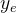
把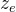
因为对于正交投影w分量不是必须的,所以正交投影矩阵的第4行为(0, 0, 0, 1)。
得到完整的正交投影矩阵如下:
如果视景体是对称的,可以进一步简化为:
即:
故正交投影矩阵被简化为: