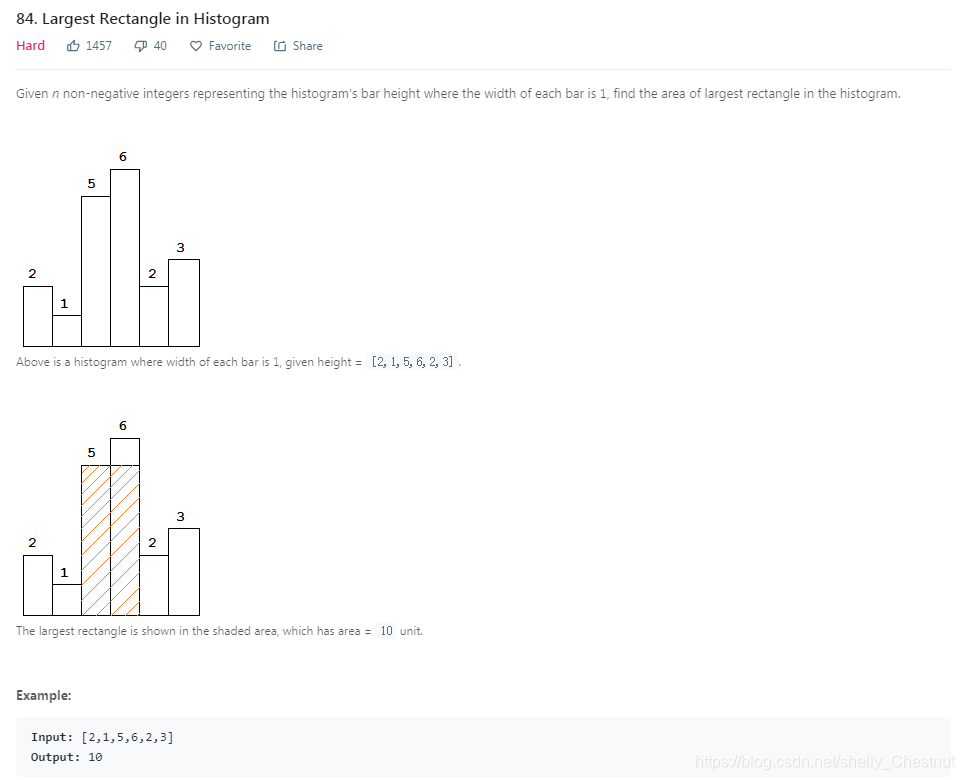
问题
分析
共有两种方法解决这个问题,先说容易想到的一种方法
分治法:
在整数序列中找到当前序列中的最小值(记其下标为mid),则整个序列的最大矩形面积可能是以下三个值中的其中之一:
1)左边(不包括mid)序列的最大矩形;
2)右边(不包括mid)序列的最大矩形;
3)以mid位置的矩形高为高,以全部序列的宽度为宽的矩形。
其中1),2)可以同样的方式递归求解。
这样就可以得出解法一(分治法一),代码贴在下面。在该解法中,每次需要遍历当前序列,以找到当前序列中最小的值。
时间复杂度:O(nlogn)(震惊!我求不出来这个值),超时。
分治法改进:
解法一中,花费了大量的时间在找到序列中最小值上;如果我们能降低找到一个序列中最小值的复杂度为O(1),则分治法的时间复杂度可以降低到O(logn)。
(wait a moment 线段树 树高logn,那么找一个区间的最小值,复杂度也应该是O(logn)才对吧……啊)
这里用到的线段树的概念。首先简单介绍线段树的概念。
线段树
线段树是一种数据结构(不然呢);它是以树结构为支撑的数组。它的每个节点记录了某个区间,如[start,end]范围内的原数组的某个性质,如该区间的最大值/最小值;该区间的和等,可根据具体问题设置节点为不同的值。该树的叶子节点即为原数组的每个元素。
下面以本题为例,介绍用线段树求某个区间的最小值的方法。
求解这个问题主要包括以下几个步骤:
1)构造线段树;
2)在线段树中找某个区间的最小值。
构造线段树:
根节点存[0,heights.length-1]区间范围内的heights数组的最小值;要想获得该节点的取值,首先需要递归的构造其左右子树,获得左右子节点的取值。则根节点取值=heights[左节点值]<heights[右节点值])?左节点值:右节点值。
记mid=low+(high-low)/2;curr记录当前节点在线段树数组中的位置。
其左子树要构造的区间为[low,mid],curr=curr2+1;其右子树要构造的区间为[mid+1,high],curr=curr2+2。
在线段树中找某个区间的最小值:
要求某个区间内的最小值,如果待求区间[left,right]恰好与当前节点对应区间[ss,se]一致,则返回当前节点的取值;
否则,在左子树中获得该区间内的最小值;在右子树中农获得该区间内的最小值,比较返回结果。
栈方法:
如果该序列是递增序列的话,那该递增序列的最大矩形,只要从后向前遍历一遍该序列,每向前一个位置,更新currArea=遍历过的长度当前位置的高度;比较保存最大的矩形即可。
如[1,2,3,4,5,6],从后向前遍历,得到的currArea分别为:16=6,25=10,34=12,43=12,52=10,6*1=6,则最大矩形为12。
但本题中不能这样解,原因在于,该序列非递增序列(em废话)。或者说,可能其中存在递增序列,但会被后面的一个元素破坏掉,如[2,1,5,6,2,3]中,1,2(第二个2)值,就是破坏递增序列的元素。
这里采取这种方法:使用一个栈;
- 从前向后遍历,如果后一个元素能保持递增特性,则该高度入栈;
- 如果后一个元素小于当前栈顶元素,则出栈,直至栈顶元素值小于后一元素值;出栈的同时,记录栈内的递增序列组成的矩形面积值,比较保存最大的面积(同开始说的递增序列中的做法);
- 计算出栈的元素个数,再入栈相同的元素个数,取值为后一元素的高度值;
- (数组中所有的元素在遍历完后,以递增的形式保存在了栈内,这个递增序列组成的矩形面积还没有计算)栈内元素出栈,同时记录矩形面积值(同开始的计算过程),比较保存最大矩形面积。
BTW,这个非最简洁的栈实现方法,TBH,其实是很烂的实现方法;
时间复杂度:O(n)
代码
分治法一:
public int largestRectangleArea(int[] heights) {
if (heights == null || heights.length == 0)
return 0;
int len = heights.length;
int ans = 0;
ans = helper(heights, 0, len - 1);
return ans;
}
private int helper(int[] heights, int left, int right) {
// TODO Auto-generated method stub
// 返回条件
if (left > right)
return 0;
if (left == right)
return heights[left];
int pivot = minHeight(left, right, heights);
int leftArea = helper(heights, 0, pivot - 1);
int rightArea = helper(heights, pivot + 1, right);
int merge = (right - left + 1) * heights[pivot];
// 比较三者大小,返回max
return Math.max(leftArea, Math.max(rightArea, merge));
}
private int minHeight(int left, int right, int[] heights) {
// TODO Auto-generated method stub
int index = left;
if (left >= right)
return left;
int mid = left + (right - left) / 2;
int leftMin = minHeight(left, mid, heights);
int rightMin = minHeight(mid + 1, right, heights);
return heights[leftMin] < heights[rightMin] ? leftMin : rightMin;
}
分治法(+线段树)
public int largestRectangleArea(int[] heights) {
// 根据heights构造segment tree
if (heights == null || heights.length == 0)
return 0;
int maxSize = getSize(heights);
int[] tree = new int[maxSize];
construct(heights, tree);
// 构造完成
return helper(heights, 0, heights.length - 1, tree);
}
private int helper(int[] heights, int left, int right, int[] tree) {
// TODO Auto-generated method stub
if (left > right)
return 0;
if (left == right)
return heights[left];
int pivot = getMinValue(left, right, tree, heights);
int leftArea = helper(heights, left, pivot - 1, tree);
int rightArea = helper(heights, pivot + 1, right, tree);
int merge = (right - left + 1) * heights[pivot];
return Math.max(rightArea, Math.max(leftArea, merge));
}
private int getMinValue(int left, int right, int[] tree, int[] heights) {
// 获得left——right之前的最小值
return getMinIndexUtil(left, right, tree, 0, heights.length - 1, 0, heights);
}
private int getMinIndexUtil(int left, int right, int[] tree, int ss, int se, int curr, int[] heights) {
if (left <= ss && right >= se)
return tree[curr];
if (left > se || right < ss)
return -1;//
int mid = left + (right - left) / 2;
// 这里为什么ss与se要变:因为树往下走,下面节点包括的区间变小,所以要变ss和se
// 为什么left和right不变:已经通过上面的两个if限制了如果left——right大于ss——se应该怎么处理,所以这里不用变
// 一知半解
int leftMin = getMinIndexUtil(left, right, tree, ss, ss + (se - ss) / 2, curr * 2 + 1, heights);
int rightMin = getMinIndexUtil(left, right, tree, ss + (se - ss) / 2 + 1, se, curr * 2 + 2, heights);
return getMin(leftMin, rightMin, heights);
}
private void construct(int[] heights, int[] tree) {
constructUtil(tree, 0, heights, 0, heights.length - 1);
}
private int constructUtil(int[] tree, int curr, int[] heights, int left, int right) {
// 构造线段树
if (left == right) {
tree[curr] = left;
return tree[curr];
}
if (left > right)
return -1;
int mid = left + (right - left) / 2;
int leftMinIndex = constructUtil(tree, curr * 2 + 1, heights, left, mid);
int rightMinIndex = constructUtil(tree, curr * 2 + 2, heights, mid + 1, right);
int min = getMin(leftMinIndex, rightMinIndex, heights);
tree[curr] = min;
return tree[curr];
}
private int getMin(int leftMinIndex, int rightMinIndex, int[] heights) {
if (leftMinIndex == -1)
return rightMinIndex;
if (rightMinIndex == -1)
return leftMinIndex;
return heights[leftMinIndex] < heights[rightMinIndex] ? leftMinIndex : rightMinIndex;
}
private int getSize(int[] heights) {
int x = (int) (Math.ceil(Math.log(heights.length) / Math.log(2)));
int max_size = 2 * (int) Math.pow(2, x) - 1;
return max_size;
}
栈方法
public int largestRectangleArea2(int[] heights) {
if (heights == null || heights.length == 0)
return 0;
LinkedList<Integer> stack = new LinkedList<Integer>();
stack.push(heights[0]);
int area = 0;
int currArea = 0;
int bottom = 0;
for (int i = 1; i < heights.length; i++) {
if (heights[i] >= stack.peek()) {
stack.push(heights[i]);
} else {
int gap = i;
while (!stack.isEmpty() && heights[i] < stack.peek()) {
int curr = stack.pop();
currArea = curr * (i - gap + 1);
if (currArea > area)
area = currArea;
gap--;
}
for (int j = 0; j < i - gap + 1; j++) {
stack.push(heights[i]);
}
}
}
int count = 1;
int top = stack.pop();
area = 1 * top > area ? top : area;
while (!stack.isEmpty()) {
count++;
int curr = stack.pop();
area = count * curr > area ? count * curr : area;
}
return area;
}