目录
前言
在c++中的容器里map和set的学习需要二叉搜索树的铺垫,也为后边的的红黑树和AVL树做铺垫,也就是说,今天主要讲搜索树的基本结构和应用。
二叉搜索树的概念
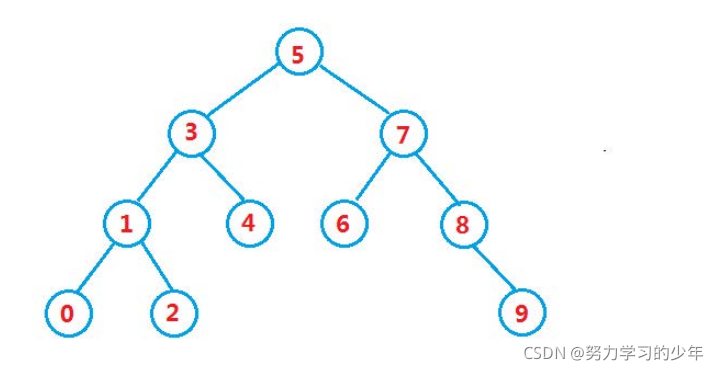
所有的根节点大于左子树的节点,小于右子树的节点的二叉树就叫做二叉搜索树。
二叉搜索的性质:
- 如果左子树不为空,则左子树上的所有节点都小于根节点。
- 如果右子树不为空,则右子树上的所有节点都大于根节点。
- 左右子树也为搜索二叉树。
假设我们要查找8,我们从根节点开始查找,这该怎样查找呢?
首先我们先与根节点5对比,发现比根节点5大,所以我们就到它的右子树查找,根节点就变为7,然后我们再与根节点7对比,发现比根节点大,再到根节点7的右子树查找,根节点就变为8,找到该节点之后我们在返回。
二叉搜索树的搜索的时间复杂度:
对于同一个元素的集合,如果元素的插入顺序不同的,则会出现不同结构的二叉搜索树,也就是说树的结构与元素插入的顺序有关。
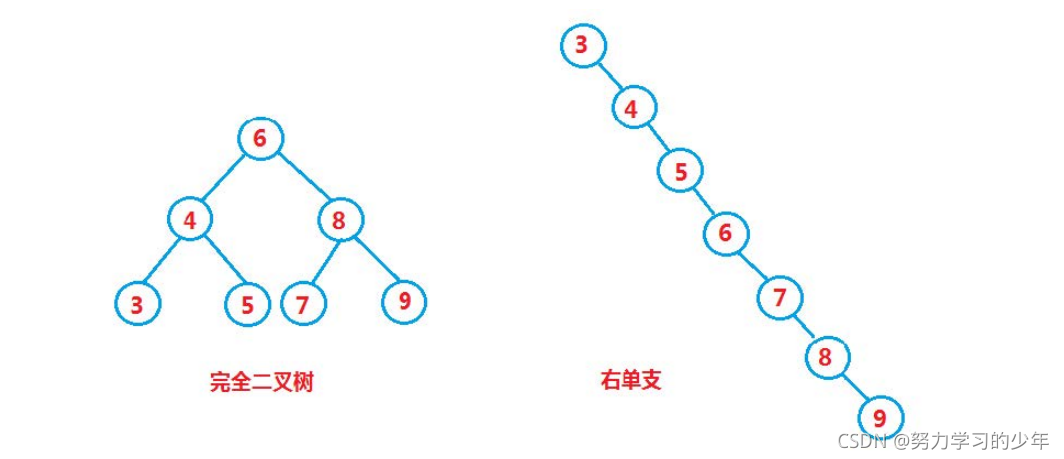
搜索效率最优的情况下:完全二叉树,其平均比较的次数是O (logN)。
搜索效率最坏的情况:单支二叉树,其平均的比较次数是O(N)
所以搜索二叉树的搜索的时间复杂度是O(N),时间复杂度看的是最坏的情况。
树的搜索次数与树的层次有关.
二叉搜索树的操作
树的节点实现
template<class T>
struct TreeNode
{
TreeNode* _left;
TreeNode* _right;
T _key;
TreeNode(const T& x)
:_key(x)
,_left(nullptr)
,_right(nullptr)
{
}
};搜索树的基本结构
template<class T>
class BinarySearchTree
{
public:
typedef TreeNode<T> Node ;
//需要构造函数将根节点初始化为空
BinarySearchTree()
:_root(nullptr)
{
}
.....
private:
//为什么是定义Node变量?
//1.插入删除时,好判断该节点是否为空。
//2.节点的左右孩子都是指针,方便赋值
Node* _root;//根节点
};
插入数据
a.树为空,则直接插入
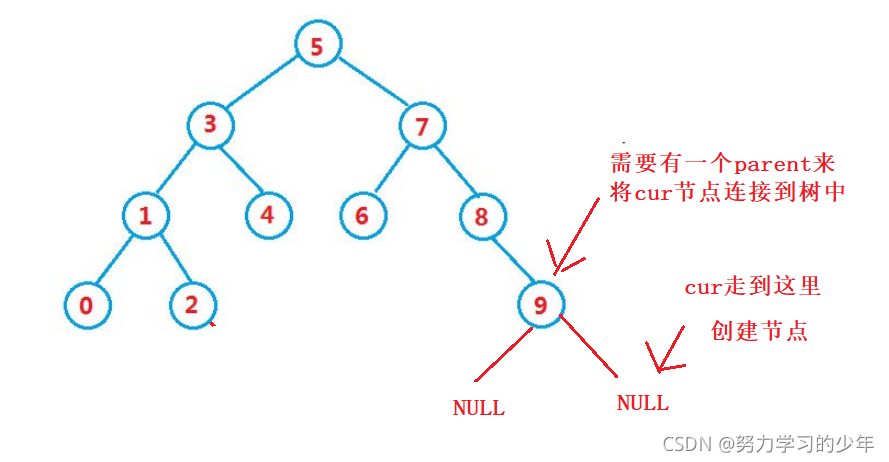
b.树不为空,按二叉树搜索的性质插入的位置,插入的位置都会是叶子节点。
c.如果插入的数据在树中已存在,则不将数据插入到树中,并返回false。搜索树的数据都是独一无二的。
代码实现:
非递归版本
bool _Insert( const T& key)
{
//如果树中已存在key,则返回false
if (_root == nullptr)
{
_root = new Node(key);
return true;
}
//遍历搜索树
Node* cur = _root;
Node* parent = nullptr;
while (cur)
{
if (cur->_key<key)
{
parent = cur;
cur = cur->_right;
}
else if (cur->_key > key)
{
parent = cur;
cur = cur->_left;
}
else
{
return false;
}
}
//创建节点,这里用了匿名对象
cur = new Node(key);
//判断cur节点要连接到parent的哪个节点
if (parent->_key > key)
{
parent->_left = cur;
}
else if (parent->_key < key)
{
parent->_right = cur;
}
return true;
}递归的版本:
//注意root是指针的引用
bool _InsertR(Node* &root, const T& key)
{
//如果节点为空,则创建节点给给它
if (root == nullptr)
{
root = new Node(key);
}
if (root->_key > key)
{
_InsertR(root->_left, key);
}
else if(root->_key<key)
{
_InsertR(root->_right, key);
}
else {
return false;
}
return true;
}
bool InsertR(const T& key)
{
return _InsertR(_root, key);
}_Insert是在private里面的,而Insert是public里的。
查找
找到了就返回该节点的地址,找不到就返回空。
Node* find(const T& key)
{
if (_root == nullptr)
return nullptr;
Node* cur = _root;
while (cur)
{
if (cur->_key > key)
{
cur = cur->_left;
}
else if (cur->_key < key)
{
cur = cur->_right;
}
else {
return cur;
}
}
return nullptr;
}
删除
当我们要删除搜索树中某个节点的时候,删除后的树的结构也需要保持着搜索的性质,所以删除有有以下4种情况、
- 要删除的节点无孩子节点。例如 0 4 6 9
只要我们找到该值,直接删除掉就行。
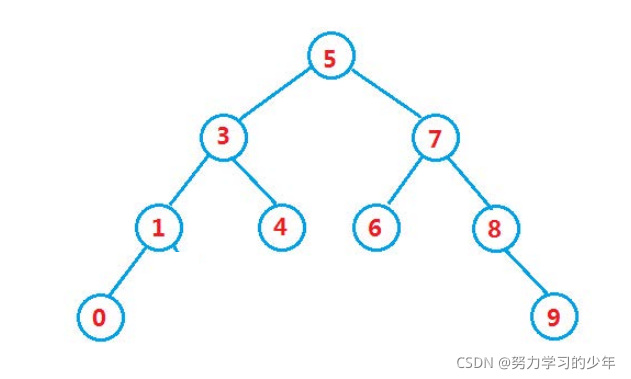
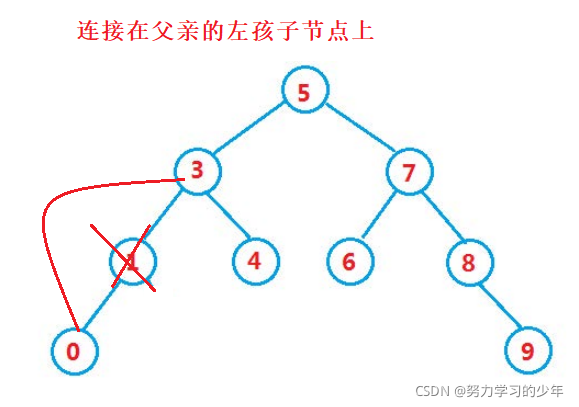
- 要删除的节点有左孩子的节点。例如 1
找到该值,先让该值的父亲节点区连接它的左孩子节点,然后再删除掉。父亲节点要连接该值的左孩子节点时,需要判断孩子节点是连接在父亲的左边还是右边
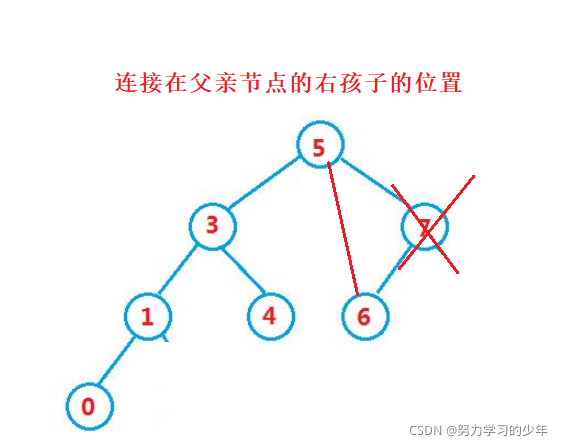
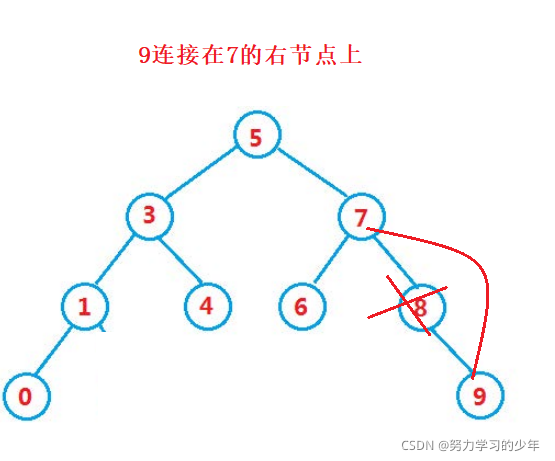
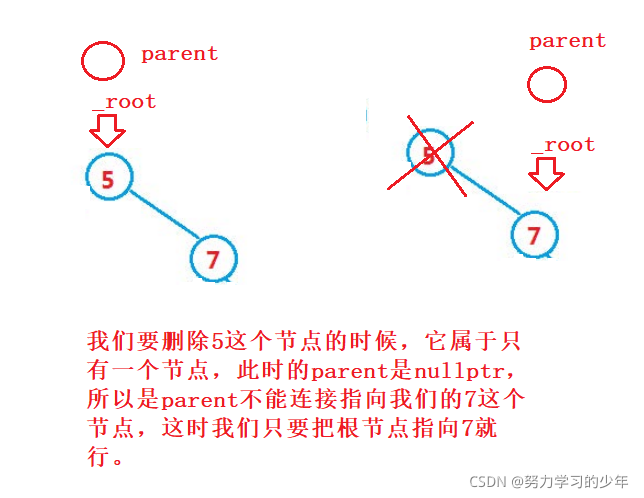
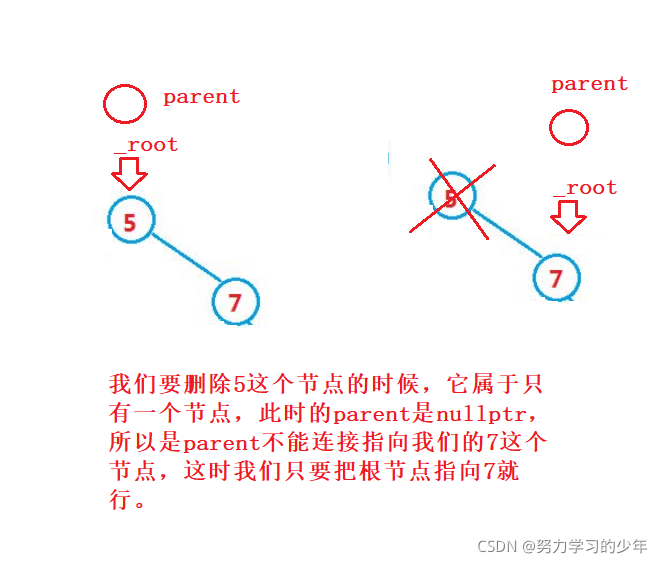
- 要删除的节点有右孩子的节点。例如 8
找到该值,先让该值的父亲节点区连接它的右孩子节点,然后再删除掉。父亲节点要连接该值的右孩子节点时,需要判断孩子节点是连接在父亲的左边还是右边
- 要删除的节点有左右孩子的节点。例如 3 5 7
如果我们直接删除这样的节点时,就会让使它的左右子树没有根节点,所以我们怎样删除这样的节点,并保持搜索二叉树的特性?
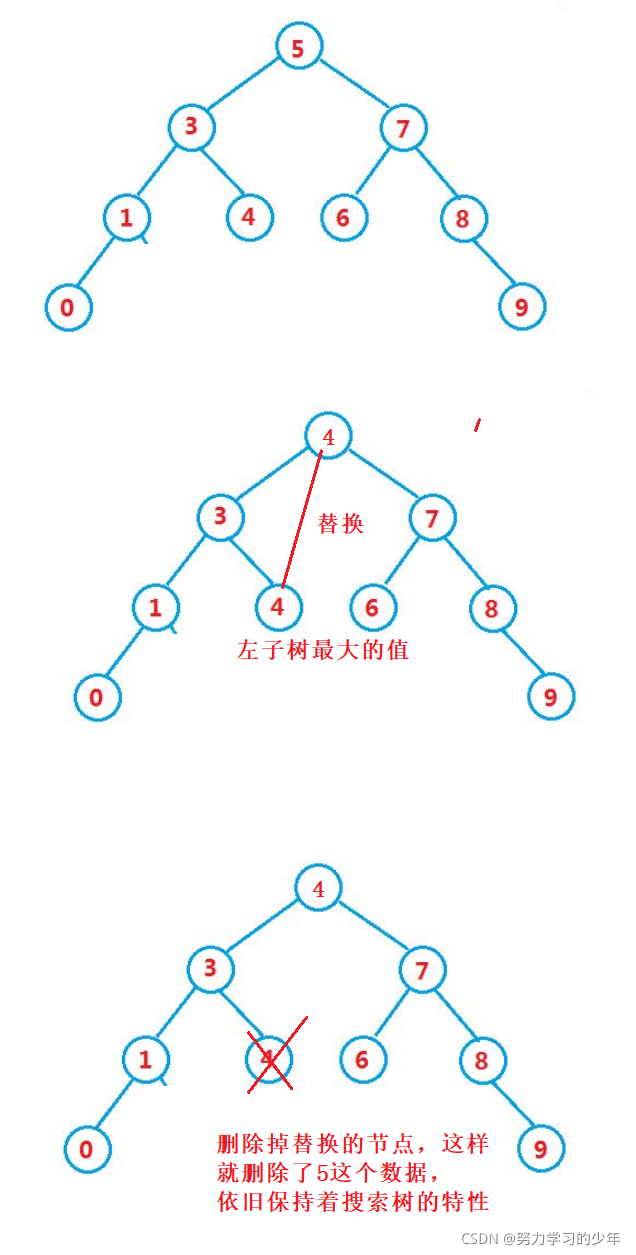
我们可以找出该值左子树最大的节点或者右子树最小的节点,去替换根节点,然后将替换的节点给删除掉。(左子树最大的节点或者右子树最小的节点去替换的根节点依旧可以保持着搜索二叉树的性质)。
删除5这个数据的过程;,找出左子树最大的值,也就是左子树最右的值,替换到根节点,然后直接将 替换的节点删除即可。
删除3的过程,找出左子树最大的值,也就是左子树最右的值。
代码:
bool _erase(const T key)
{
if (_root == nullptr)
return false;
//找出key的节点
Node* cur = _root;
Node* parent = nullptr;
while (cur)
{
if (cur->_key < key)
{
parent = cur;
cur = cur->_right;
}
else if (cur->_key > key)
{
parent = cur;
cur = cur->_left;
}
else {
break;
}
}
//第一种:删掉的是叶子节点
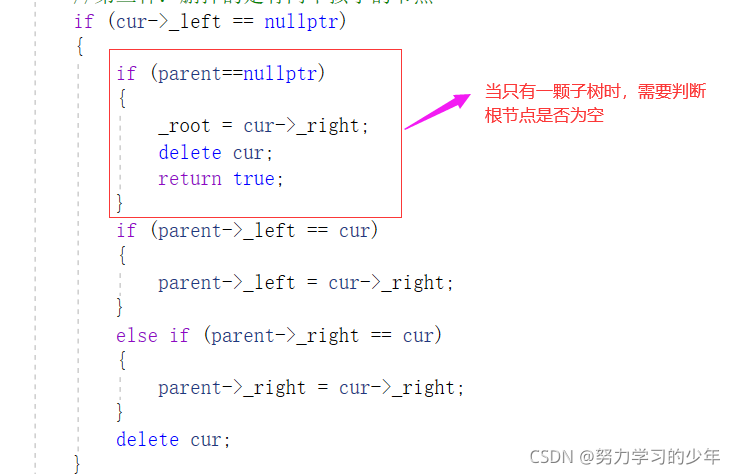
//第二种:删掉只有一个孩子的节点
//第三种:删掉的是有两个孩子的节点
//删除只有右孩子的节点
if (cur->_left == nullptr)
{
if (parent==nullptr)
{
_root = cur->_right;
delete cur;
return true;
}
if (parent->_left == cur)
{
parent->_left = cur->_right;
}
else if (parent->_right == cur)
{
parent->_right = cur->_right;
}
delete cur;
}
//删除只有左孩子的节点
else if (cur->_right == nullptr)
{
if (parent == nullptr)
{
_root = cur->_left;
delete cur;
return true;
}
if (parent->_left == cur)
{
parent->_left = cur->_left;
}
else if (parent->_right == cur)
{
parent->_right = cur->_left;
}
delete cur;
}
//删除有左右孩子的节点
else
{
//第三种情况
Node* leftmax = cur->_left;
Node* leftmaxparent = cur;//左子树最大节点
//找出左子树最大的节点
while (leftmax->_right)
{
leftmaxparent = leftmax;
leftmax = leftmax->_right;
}
//赋给根节点
cur->_key = leftmax->_key;
//删除节点
if (leftmaxparent->_left == leftmax)
{
leftmaxparent->_left = leftmax->_left;
}
else {
leftmaxparent->_right = leftmax->_left;
}
delete leftmax;
return true;
}
return false;
}
这段代码的含义:
递归版本:
bool _eraseR(Node* &root,const T key)
{
//查找key相对应的值
if (root == nullptr)
return false;
if (root->_key < key)
_eraseR(root->_right, key);
else if (root->_key > key)
_eraseR(root->_left, key);
else {
if (root->_left == nullptr)
{
Node* tmp = root;
root = root->_right;
delete tmp;
}
else if (root->_right == nullptr)
{
Node* tmp = root;
root = root->_left;
delete tmp;
}
else
{
//第三种情况
Node* leftmax = root->_left;
Node* leftmaxparent = root;
//找出左子树最大的节点
while (leftmax->_right)
{
leftmaxparent = leftmax;
leftmax = leftmax->_right;
}
//赋给根节点
root->_key = leftmax->_key;
//删除节点
if (leftmaxparent->_left == leftmax)
{
leftmaxparent->_left = leftmax->_left;
}
else {
leftmaxparent->_right = leftmax->_left;
}
delete leftmax;
return true;
}
}
return false;
}
bool eraseR(const T& x)
{
return _eraseR(_root, x);
}_eraseR是private里面的,eraseR是public里面的。
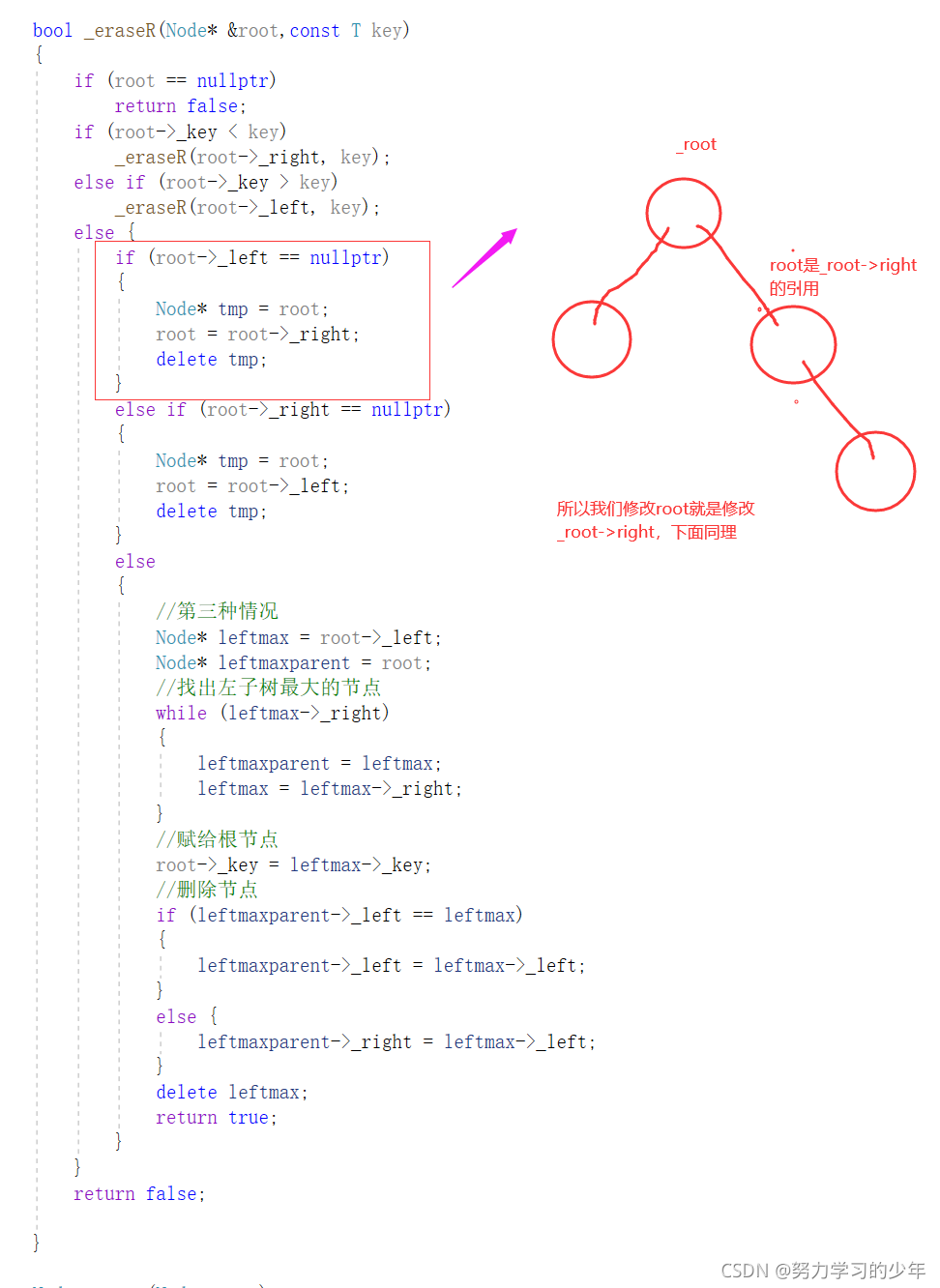
eraseR是对_eraseR的封装,方便被调用。
拷贝构造函数
Node* _copy(Node* root)
{
if (root == nullptr)
return nullptr;
Node* copyroot = new Node(root->_key);
copyroot->_left=_copy(root->_left);
copyroot->_right=_copy(root->_right);
return copyroot;
}
BinarySearchTree(BinarySearchTree<T>& t)
{
_root=_copy(t._root);
}赋值重载函数
析构函数:
void Destory(Node* root)
{
if (root == nullptr)
return;
Destory(root->_left);
Destory(root->_right);
delete root;
}
~BinarySearchTree()
{
Destory(_root);
_root = nullptr;
}2.4 二叉搜索树的应用
1.K模型:K模型只有key作为关键码,也就是定义树的节点只需要存_key一个即可,关键码即为搜索到的值。如上我们写的搜索树就是k模型,因为树的节点就只有一个key可以存储数据。
比如:我们要进学校的图书馆就需要刷我们的学生卡,通过磁感应将门打开。如下:
此时我们就需要先将学生的学号录入到该门的管理系统,然后将数据建立起搜索树,我们的学号在学校是唯一的,当我们刷卡的时候,就会去管理系统快速查找我们的学号,找到了门就开了。
k模型在实际应用中就是就是查找在不在的问题。
2.kv模型:每一个关键码key都有一个对应的value值,也就是说树的节点中有两个值,一个是key,一个是value的值,我们通过key找到对应的节点,然后将相对应的value给映射出来。也就是说,我们增删查改的时候也是按key进行插入或者删除。只是创建节点,增加了一个value值。
场景1:我们去网上买高铁票,每张高铁票的信息都有与一个身份证号绑定在一起的,当我们进高铁站都需要刷身份证在搜索树中查找有没有你的身份证号,找到了,通过身份证号映射你的高铁信息,看看有没有你的班次,门才是否可以被开。在这里_key是身份证,它是独一无二的,_value是高铁信息,通过身份证将它给映射出来。
场景2:
英汉词典就是英文与中文的对应关系,我们只需要查找有没有该英文,找到了,就通过映射关系,将该英文的单词的中文给映射出来。
用kv模型的搜索树写一个简单的词典:
int main()
{
BinarySearchTree<string ,string> v;
v._Insert("string","字符串");
v._Insert("apple","苹果");
v._Insert("automate", "n.自动化,v.使自动化");
v._Insert("voluntary", "adj.自愿的主动的,n.志愿者");
string s;
while (cin>>s)
{
struct TreeNode<string,string>* ret = v.find(s);
if (ret == nullptr)
{
cout << "没有找到该单词" << endl;
}
else
{
cout <<endl << " 中文:" << ret->_value << endl;
}
}
return 0;
}运行结果:
场景3:
统计水果次数。
如下
int main()
{
const string str[] = { "苹果","西瓜","芒果","苹果","西瓜","西瓜","西瓜","苹果","芒果" };
BinarySearchTree<const string, int> count;
for (auto s : str)
{
auto ret = count.find(s);
if (ret == nullptr)
{
count._Insert(s, 1);
}
else {
ret->_value++;
}
}
count.Inorder();
return 0;
}输出结果:
其中Inorder是将树中所有的节点都给打印出来,代码如下:
void _Inorder(Node* root)
{
if (root == nullptr)
return;
_Inorder(root->_left);
cout << root->_key << ":" << root->_value << endl;
_Inorder(root->_right);
}
void Inorder()
{
_Inorder(_root);
}_Inorder是private里面的,而Inorder是public里面的。
好了,今天分享的知识就到这里了,喜欢的小伙伴们,麻烦帮我点个三连,谢谢你们了。