目录
1.程序功能描述
一维信号的小波变换与重构算法matlab仿真,对正弦测试信号进行小波变换,然后进行重构,然后计算重构之后的信号与原信号的误差。
2.测试软件版本以及运行结果展示
MATLAB2022A版本运行
(完整程序运行后无水印)
3.核心程序
...............................................................
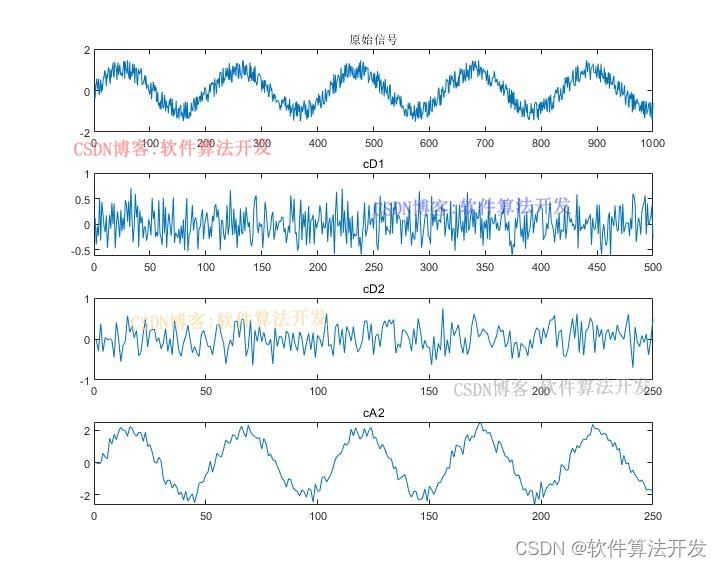
% 绘制分解后的各个系数图像
figure
subplot(411)
plot(x);title('原始信号');xlim([0,length(x)]);
subplot(412)
plot(cD1);title('cD1');xlim([0,length(x)/2]);
subplot(413)
plot(cD2);title('cD2');xlim([0,length(x)/4]);
subplot(414)
plot(cA2);title('cA2');xlim([0,length(x)/4]);
% 一维小波重构过程
% 对低频系数cA1进行上抽取(补零操作)
upl=func_up_sample(cA1);
% 对上抽取后的信号使用低通滤波器进行重构
cvl=func_wlfilter(upl,Lw);
% 对高频系数cD1进行上抽取(补零操作)
uph=func_up_sample(cD1);
% 对上抽取后的信号使用高通滤波器进行重构
cvh=func_wlfilter(uph,Hi);
% 将低频和高频重构部分相加以得到最终重构信号
yst=cvl+cvh;
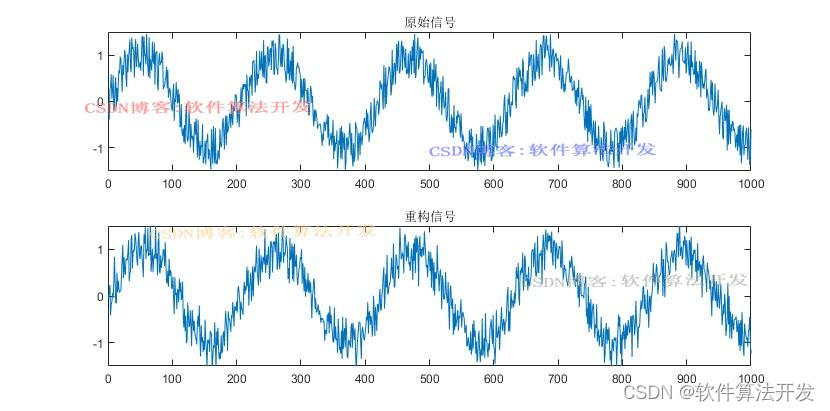
% 绘制重构信号与原始信号的对比图
figure
subplot(211)
plot(x);title('原始信号');axis([0 1000 -1.5 1.5]);
subplot(212)
plot(yst);title('重构信号');axis([0 1000 -1.5 1.5]); % 设置重构信号的坐标轴范围
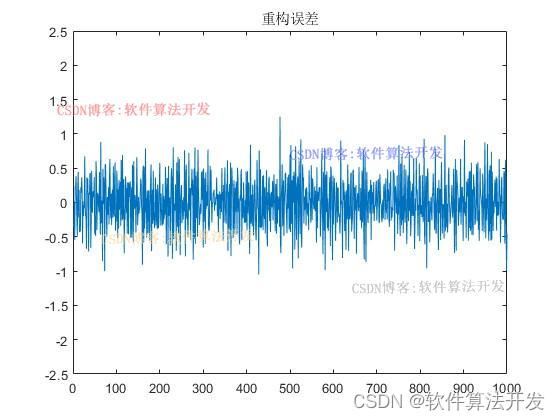
%重构误差
figure
plot(x-yst(1+6:length(x)+6));title('重构误差');axis([0 1000 -2.5 2.5]);
634.本算法原理
一维信号的小波变换是一种时频分析方法,它通过在不同的尺度上分析信号,以捕捉信号的局部特征和时频结构。小波变换能够提供时间局部化和频率局部化的信息,这对于非平稳信号的分析尤为有效。小波变换的核心思想是使用一族具有多分辨率特性的基函数——小波基,这些基函数在时间和频率上都有局部化特性,既能在时间域聚焦于信号的某一局部,也能在频率域集中于某一频带。
4.1 小波变换原理
4.2 离散小波变换(DWT)
在实际应用中,连续小波变换计算量巨大,因此通常采用离散小波变换(Discrete Wavelet Transform, DWT)来简化计算。DWT通过在时间域和尺度域进行量化,将连续小波变换离散化。最常用的离散小波变换方法之一是Mallat算法,也称为塔式算法。
小波包变换(Wavelet Packet Transform, WPT)是对DWT的扩展,它不仅在尺度上进行分解,还在每个尺度上同时进行频率分割,使得在每个尺度上都能获得不同频率带的信息。小波包变换能够提供更细粒度的频带分析,适合于信号中包含多种频率成分的情况。
其中,分解过程中的卷积和降采样操作可以用公式表示为:
其中,x[k]是原始信号的样本,h[n]和g[n]分别是低通和高通滤波器的系数。
小波重构是分解过程的逆过程,涉及上采样和卷积:
一维信号的小波变换通过选择合适的小波基函数和利用Mallat算法,可以在不同尺度上提取信号的特征,实现信号的时频分析。小波变换不仅在信号去噪、压缩、特征提取等方面有广泛应用,而且在图像处理、数据压缩、生物医学信号分析等领域也显示出强大的优势。小波包变换作为小波变换的扩展,进一步提高了信号分析的灵活性和精确度。
5.完整程序
VVV