最近的面试中,数据结构被吊打了很多次。之前蚂蚁金服被加面,也是因为四面的面试官对我的评价是:数据结构和算法不扎实。
数据结构是大学学过的基础课。当时年少无知,无法理解数据结构的重要性,学的也不怎么好。不精通就不足以支撑面试了。(当然学任何知识都不是为了应付面试的,这一点一定要清楚)只不过作为初级开发,像我这样刚从大学毕业两年的,不去写中间件之类的。说实话挺少用到数据结构这些东西。因为实际上的开发工作,更多的是运用到的都是开发语言为我们写好的集合。
在正式写之前,先解释一下,为什么说是基本数据结构。所谓基本数据结构,它不跟语言挂钩。算计程序设计的基础。数据结构是,是数据资质方式的一种抽象概念。而基本数据结构,其实是相对比较简单,又很重要,特别是对于一个初级开发人员来说,实际上就是找那个一种数据结构来解决我们的业务问题。数据结构的最大的用处,就是用特定的数据组织方式,来解决特定的场景问题。而基本数据结构,用来描述的相对简单问题,但是使用又很频繁的结构。它是初级程序员,必备的技能。数据结构行不行,直接决定了代码能不能写好。
有人说不会数据结构,不耽误写代码。我只能说,你能写的代码只是语言的判断逻辑。没有数据结构的代码,是没有灵魂的!
第一个问题:我要不要学数据结构,对我coding有用么?
如果你的征程是数据库CRUD。不学也罢。别看下去了,浪费时间,不如打把王者快乐。
如果你的征程是写出优秀的属于自己的开源中间件,或者框架。那就要好好学一下了,数据结构在你面临一些难题的时候,或许能帮上忙!
数据结构之“万物归宗”
一切数据结构要解决的问题都是一致的:维护数据的增删改查 。
不变的目的:要么降低空间复杂度,要么降低时间复杂度。二者通常情况下是此消彼长的问题。
数据结构是程序设计的基础,和语言不挂钩。通常各种语言都会基于这些数据结构有自己的api实现。
学数据结构都要学哪些
- 要学全部基础数据结构都有哪些。技术视野。
- 要知道这些数据结构的特点。有什么特长,能拿来做什么。
- 最好知道这些数据结构的增删改查的过程。时间复杂度。
- 最后能够自己实现一遍这些数据结构。
多用对比的方法去学习数据结构
比如这个问题:二叉树,平衡二叉树,完全二叉树,B+树,红黑树,这些各有什么特点?我们应该如何去选用它们。它们适合用在什么场景?
数据结构选用原则
要知道我们的目的是什么?
- 做查找?
- 做增删?
针对上边提出的问题,延伸一下
- 如何做到查找时间复杂度 O(1)
- 如何做到增删的时间复杂度O(1)
O(1)是最佳的时间复杂度,没有比这更小的时间复杂度了。
针对上述问题再延伸,实际上对了两种数据结构雏形
- 数组。本质上是一块连续的存储空间。通过下标的方式来获取到数据。适合做根据下标的数据查询。根据下标查找时间复杂度 O(1)。不适合做修改和插入(如果是插入到数组的尾端还行)
- 链表。本质上是一个一条链。每个数据节点都有指针,来记录它的前一个节点和后一个节点。适合数据的增删改。时间复杂度 O(1)。
- 折中的结构,hash表。通过计算存储数据的下标的形式,来维护数据。数据插入时间复杂度为 O(1),增删的时间复杂度O(1)。弊端是,有一个扩容的过程,和rehash的过程。推荐看一下java中HashMap的源码。
基本数据结构家族成员
- 数组
- 链表
- 树相对来说是家族成员最复杂度。
- 二叉树
- 完全二叉树
- 满二叉树
- 平衡二叉树
- B-Tree
- B+树
- B*树
- R树
- Trie树
- 红黑树
- 森林
- 图
- 栈
- 堆
- 大根堆
- 小根堆
- 队列
树详解
树
- 有且仅有一个特定的称为根的结点。
- 当n>1时,其余节点可分为m(m>0)个互不相交的有限集T1,T2,…,Tm,其中每个集合本身又是一棵树,并且称为根的子树。
- 显然,树的定义是递归的,即在树的定义中又用到了自身,树是一种递归的数据结构。树作为一种逻辑结构,同时也是一种分层结构,具有以下两个特点:
- 树的根结点没有前驱,除根结点外的所有结点有且只有一个前驱。
- 树中所有结点可以有零个或多个后继。
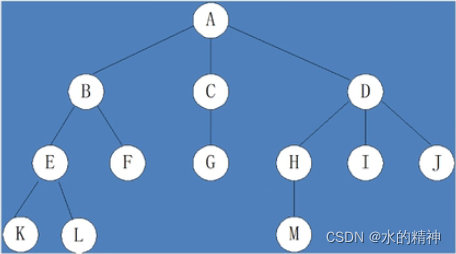
树就长这样。很抽象就和我们看到的马路边上的树差不多。只不过是倒过来的!
树的常见案例
- 目录结构是躺着的树。
- 我们做的web系统的菜单。
二叉树
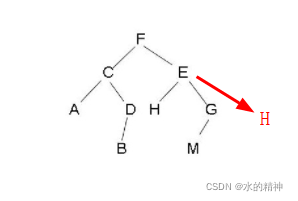
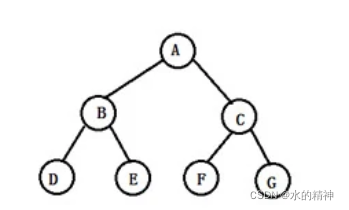
二叉树的定义是:是指树中节点的度不大于2的有序树(白话理解就是:最多两个树杈)。意思是:每个节点最多有两课子树。例如下图,如果我多加一个红色箭头指向的节点H。则不是二叉树。
这里提到了度,还是说一下:什么是度?例如:F下边只有两个节点,如果下图没有H这个节点的话,我们可以说,它是二叉树。如果加上H,那就不是二叉树了,二叉树的定义是,任意节点的直系孩子节点最多能有两个。
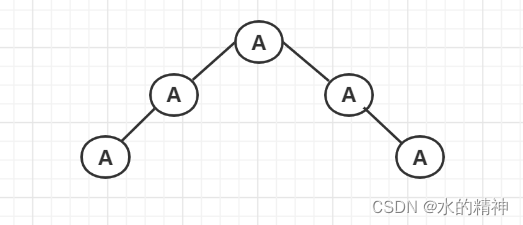
二叉树会有一个问题:在极端情况下,根节点的左孩子只有左孩子,根的右孩子永远只有右孩子,则会演变成链表的形式。
完全二叉树
完全二叉树,是二叉树中的一种特殊的结构。
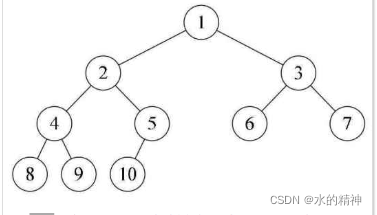
完全二叉树是以特定顺序来存放节点数据的。它的顺序是从上至下,从左至右。将每一层放满以后再放下一层。并且每一层也是从左向依次放入。
- 放满一层再放下一层。
- 从左向右,依次填满。
假如上图,去掉 6节点,则不是完全二叉树。因为不满足放满一层再放下一层的条件。假如去掉节点9,也不叫完全二叉树。因为不满足,从左向右依次填满的条件。
满二叉树
一个二叉树的深度为K,且结点总数是(2^k) -1 ,则它就是满二叉树(这是国内对满二叉树的定义)。
通过推论,我们可以看出来。满二叉树一定是完全二叉树。
平衡二叉树
平衡二叉树是为了解决二叉查找树可能退化成链表问题。平衡二叉树也叫自平衡二叉搜索树(Self-Balancing Binary Search Tree)。
平衡二叉树的特点就是:所有节点的左右子树高度差的绝对值不超过1。如果不满足,则需要进行调整,调整成满足条件的树。
平衡二叉树应用场景:修改少,查询多的情况。它的查询时间复杂度为:O(log n) 可以看详解:平衡二叉搜索树查找的时间复杂度为什么是O(log n)?_zhangjin1120的博客-CSDN博客_二叉搜索树搜索时间复杂度
平衡二叉树的缺点:插入过程因为要自平衡,调整的过程比较耗时。
实现平衡二叉树关键点
- 什么时候去自平衡?也就是对平衡二叉树的定义:满足任意节点的左右子树的高度差不超过1。所以实现平衡二叉树的第一步是:检查是否满足条件。
- 当不满足的时候就需要自动调整。其实是一个左旋和右旋的过程
自平衡详细过程
B-Tree
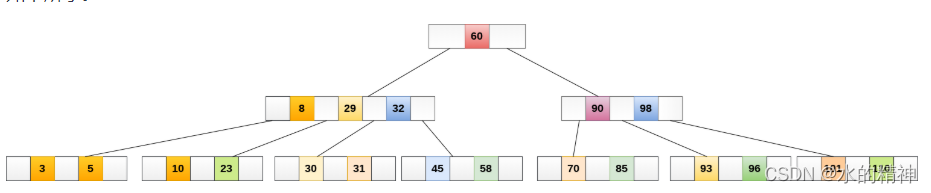
B-Tree是树中的一种特殊结构,它的特殊点,在于树会右很多个树杈。如下图。
B-Tree的结构特点,实际上在节点总数一定情况下,可以通过增加树的广度,来降低树的深度。 (如果不能理解的话,假如人的体重都是75KG,如果长的高有点,那就瘦一点。如果长的矮一点,那就胖一点。)B-Tree就是胖一点的典例。
B-Tree 中的B是平衡()
PS~ 补一下短板。过程既痛苦又快乐。明天继续干吧。(要相信没有做不好的事情)
数据结构中的常见问题
查找
增删改