量化投资分析平台 迅投 QMT
迅投 QMT
我目前在使用
两个月前(2024年4月)迅投和CQF有一个互动的活动,进行了平台的一个网上路演,刚好我也去听了,感觉还是挺不错的。后来与“客服麻瓜”进行了对QMT的深入了解和使用,最后决定买了他们的服务。注册就可以进行试用,但是是有期限的。如果只是单方面的研究的话,还是建议用稍微便宜些的平台,我主要是需要期权的实时数据进行分析和交易。
什么是BSM模型
CQF课程
CQF的模块M3会着重讲解BSM模型,其推导的过程,计算的流程和方法,BSM代码,蒙特卡洛模拟,等等。知识量大且非常丰富。感兴趣的同学可以看看我的CQF相关帖子。
介绍
布莱克-舒尔斯模型(英语:Black-Scholes Model),简称BS模型,又称布莱克-舒尔斯-墨顿模型(Black–Scholes–Merton model),是一种为期权或权证等金融衍生工具定价的数学模型,由美国经济学家迈伦·舒尔斯(Myron Scholes)与费雪·布莱克(Fischer Black)首先提出,并由罗伯特·墨顿(Robert C. Merton)修改模型于有派发股利时亦可使用而更完善。由此模型可以推导出布莱克-舒尔斯公式,并由此公式估算出欧式期权的理论价格。此公式问世后带来了期权市场的繁荣。该公式被广泛使用,虽然在很多情况下被使用者进行一定的改动和修正。很多经验测试表明这个公式足够贴近市场价格,然而也有会出现差异的时候,如著名的“波动率的微笑”。
该模型就是以迈伦·舒尔斯和费雪·布莱克命名的。1997年迈伦·舒尔斯和罗伯特·墨顿凭借该模型获得诺贝尔经济学奖。然而它假设价格的变动,会符合高斯分布(即俗称的钟形曲线),但在财务市场上经常出现符合统计学肥尾现象的事件,这影响此公式的有效性。
模型的五个重要的假设
- 金融资产价格服从对数正态分布,即金融资产的对数收益率服从正态分布;
- 在期权有效期内,无风险利率和金融资产收益变量是恒定的;
- 市场无摩擦,即不存在税收和交易成本;
- 金融资产在期权有效期内无红利及其它所得(该假设后被放弃);
- 该期权是欧式期权,即在期权到期前不可实施。
模型公式
BSM模型是一类二阶偏微分方程,具体推导我就不详细展开了。感兴趣的同学可以自行查找,视频网站上有很多。
经过一系列的推导后我们将获得几个等式的信息,这些信息就是我们编程的基础。
- C是Call购期权的价格,
- Put沽的期权价格把C等式中减号两边对调,d1和d2取负值即可
- S是标的资产的价格
- K是行权价
- r是无风险利率
- t是距离行权日所剩的日期
- N是正态分布概率
我们为啥要学(知道)这玩意儿呢?
其实我们对于模型产生出来的期权的价格并不感兴趣,因为那只是个理论上的数值,拿着理论价格取投资肯定是不行的。我们学习公式的主要原因是为了计算隐含波动率和希腊字母。
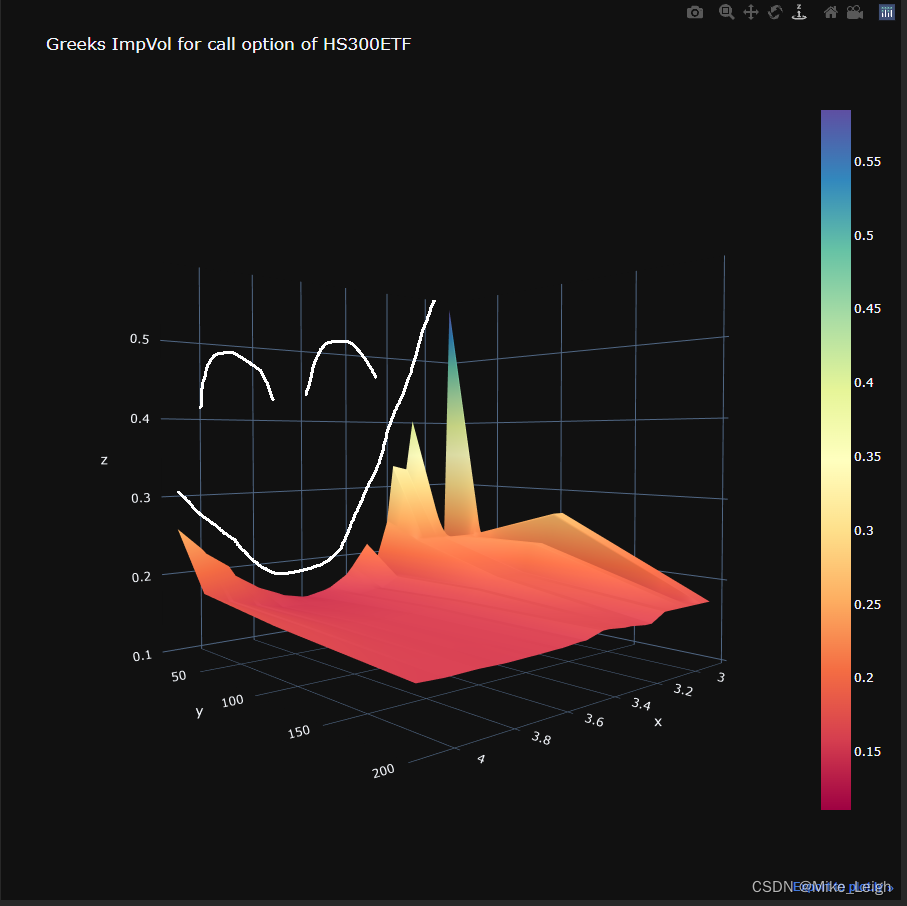
隐含波动率(Implied Volatility)
隐含波动率(Implied Volatility)是将市场上的期权或权证交易价格代入权证理论BSM模型,反推出来的波动率数值。由于期权定价模型给出了期权价格与五个基本参数(标的股价、执行价格、利率、到期时间、波动率)之间的定量关系,只要将其中前4个基本参数及期权的实际市场价格作为已知量代入定价公式,就可以从中解出惟一的未知量,其大小就是隐含波动率。感兴趣的朋友可以去看看关于隐含波动率微笑的相关书籍。根据我上一帖或第五帖的相关知识,我们知道期权分OTM, ATM, ITM,即虚值期权,平值期权,实值期权。以平值期权的隐波为中心,向两边OTM,ITM扩散,隐波的图将会是一个诡异的微笑的图案,哈哈哈哈哈,即隐波的微笑。
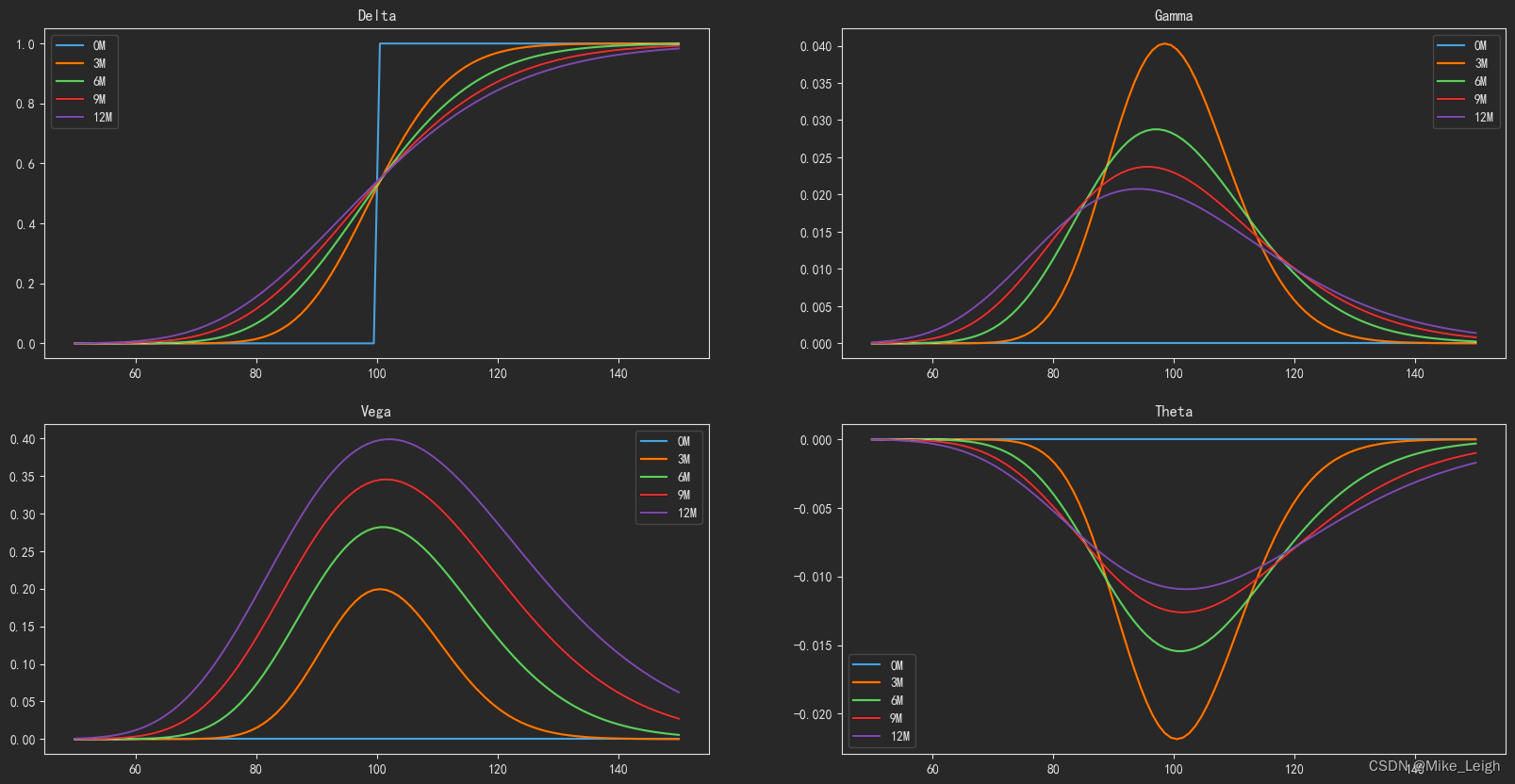
希腊字母(Greeks)
低阶:delta、gamma、vega、theta、rho
高阶:vanna、zomma、speed、ultima、等等
希腊字母是通过BSM模型的一系列计算来观测的一些比率。
- delta观测的是期权价格变动与底层资产价格变动的指标;
- gamma观测的是delta的变化速度,也就是期权价格变化与底层资产价格变动的加速度;
- vega观测期权价格与隐波的关系;
- theta观测时间价值变化(卖方的最爱,买方的噩梦)
- rho观测利率变动(基本上不关心这个)
- 高阶我只讲一个vanna,测试的是期权价格的变动,基于标的资产和隐波的变动所带来的变化;
- 高阶字母有很多,期权玩儿high了也可以非常花式,大家可以自己去学习。
下一讲上BSM的代码讲解!
希望大家能够给予一键三连啥的,您的鼓励就是我最大的动力!
历史帖子
量化投资分析平台 迅投 QMT(一)激活python迅投对接端口
量化投资分析平台 迅投 QMT(二)服务器端订阅下载数据
量化投资分析平台 迅投 QMT(三)字典数据下载后读取成Dataframe形式
量化投资分析平台 迅投 QMT(四)获取标的期权的代码
量化投资分析平台 迅投 QMT(五)我对期权的理解和定义,普及向,无代码