主要介绍了基于曲线曲度的角点检测方法，不仅介绍了早期的曲度计算方法，还包括了CSS方法、CPDA方法、样条曲线参数估计曲度方法、协方差矩阵估计曲度方法等，最后还给出了针对这些方法最新的一些改进，如基于小波、基于多尺度乘积、自适应角度阈值、动态迭代ROS等等。
一旦我们知道边缘每点的曲度，那么我们就能非常好的区分角点。通过计算曲线曲度或者可以衡量曲度的其它量，自然而然成为我们检测角点的一种方法。
传统的基于曲线的角点检测方法一般操作在二值边缘图中，这些边缘图都是由前期边缘检测获得。所以这类方法一般都包含了五个步骤：边缘提取、曲线平滑、曲度估计、找到角点、及角点追踪（从粗尺度到细尺度）。曲线平滑及曲度估计这是这个方法非常关键的步骤，平滑曲线可以减少量化噪声（高斯滤波器最为常用），而曲度估计则关系到检测角点的正确于否。
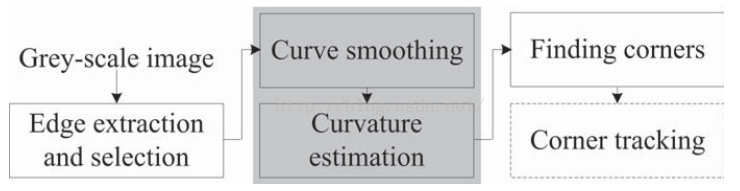
基于曲线曲度估计的角点检测方法的一般性步骤如下：
（1）首先通过边缘提取算法（如Canny等）获得二值边缘图
（2）然后根据连接相邻的边缘获得轮廓，并检测出T-连接
（3）接下来，我们考虑一组边缘序列：
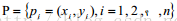这些点在边缘上相邻排列，然后我们可能会为每点建立一个支撑区域ROS（region of support）作为计算该点曲度的区域（基于ROS的方法），然后我们在该区域下应用曲度计算。
（5）提高角点位置精度（一般如CSS，可采用更高尺度下到较低尺度下追踪角点）
（6）增加曲度估计无法识别的角点（如比较T-连接和其它角点，移除两个接近角点的一个）
下面我们重点介绍下曲线曲度估计的方法
一、早期的曲度估计方法
早期曲度估计方式是直接将点同其相邻两点的夹角余弦作为曲度的衡量，不过这样方式非常容易受到噪声的影响，所以很快就提出将同相邻两点的夹角，改成同其ROS区域最远端的两点夹角，如下公式：
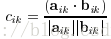
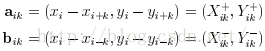
为了提高鲁棒性，也进一步消除噪声的影响，RW75方法提出了使用的平均k余弦值，其公式改进如下：
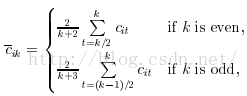
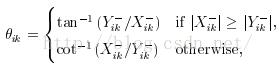
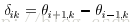
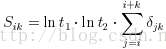
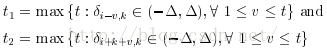
以上指的是前后两边，作为最大的空间可以保持曲度增长不变（在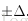
另外，BT87方法对FD77方法进行了一些改进，其对t增加了一些限制，使其不要太大。
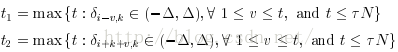
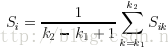
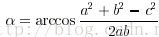
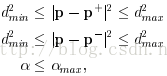
二、曲线参数估计方法
一旦我们知道边缘曲线的参数形势，那么我们要知道每点的曲度就不再困难了，比较常见的就是通过样条曲线来插值边缘点，通过估计曲线参数，然后要每点的曲度计算就简单了：
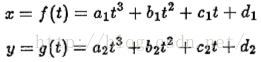
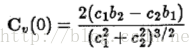
B-样条曲线的x,y可以建模成：
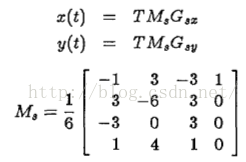
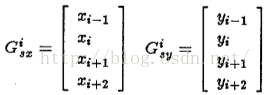
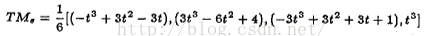
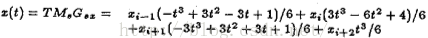
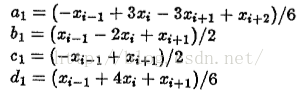
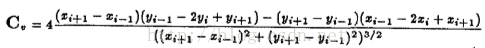
三、使用协方差矩阵的来估计曲度
边缘序列
中某点，其同其相邻的点梯度变化关系必然是相关的，由此我们可以通过计算其在ROS区域的协方差矩阵来确定曲度，ROS区域定义：
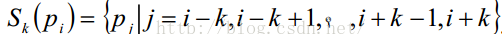
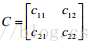
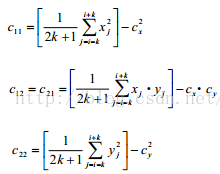
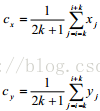
然后计算上述矩阵的两个特征值如下：
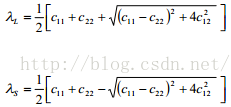
这两个特征值可以用来提取曲线形状信息：
（1）如果S的区域是直线，则最小的特征值为0，此时可以直接排除其为角点的可能
（2）如果S的区域是椭圆，则一大一小，并恰好反映长短轴的大小
（3）如果S的区域是圆，则特征值相等
因此最小的特征值大小将区分每一个边缘点的其在曲线分割区域的形状。如果其大于一个特定的阈值，那么我们可以接着进行下面的判定。
计算协方差特征值向量：
由此我们可以计算出该点曲度
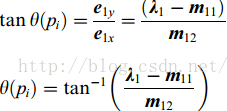
该点的角度如下计算
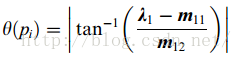
支撑区域ROS的大小k值对于结果有较大影响。如果k值越大，那么点间的相互影响就越大，起到了平滑的作用，容易造成小的特征点被误删除。如果k值越小，那么对于噪声点的敏感程度就越高。
四、CSS方法
CSS方法主要是基于如下曲度计算公式的：
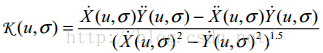
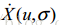指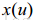
卷积一阶高斯梯度模板，而
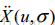指卷积二阶高斯梯度模板
考虑那些局部最大值作为角点候选（其曲度绝对值一般高于t，且两倍大于其邻域的局部最小值），然后再从更高尺度下到较低尺度下追踪角点，提高角点位置精度。最后比较T-连接和其它角点，移除两个接近的角点（或T-连接）中一个。
在这个算法里面，检测过程只用了一个尺度，而多个尺度只是在提高精度位置时使用，正如所提到的，如果尺度特别大，可以检测不出真实的角点，而尺度太小，又容易检测出噪声，另外一个问题就是固定的阈值t，容易造成错误检测。
五、CPDA方法
CPDA方法并没有直接计算曲线的曲度，因为直接计算曲度一方面计算大，另一方面容易造成误差，所以CPDA通过计算点同弦的距离来模拟曲度，从而确定角点，其是一种类曲度的检测方法。其方法具体如下：
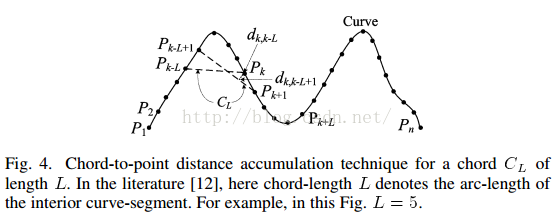
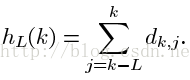
因为弦长对于检测特征点的影响特别大，而单一的L很难检测多个不同类型的特征。
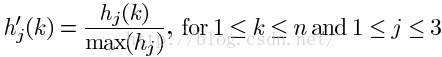
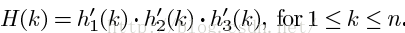
然后我们还需要计算每个角点的角度（方法同CSS方法一致），并同一个角度阈值比较，删除错误角点。最后将T形角点同其它角点比较（方法也同CSS方法一样）。
六、自适应的角度阈值同自适应的ROS区域
角度（或曲度）阈值和ROS区域对基于曲线曲度的检测方法非常重要，这类几乎每个方法都用到这两个因子。
（1）自适应局部角度阈值t
角度阈值通常是不稳定的，对于角点候选来说，虽然其因为局部最大而被提取出来，但是其同其邻域的点的曲度差别通常比较小，这是圆角点的例子，如果差别太大的话，有可能是噪声点。由此，我们定义一个新的自适应局部阈值，如果局部最大曲度绝对值小于这个阈值，将这个点移除：
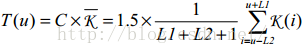
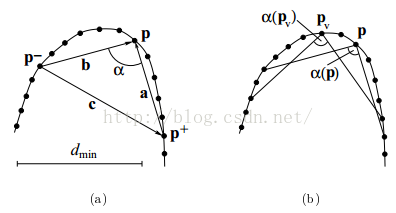
（2）动态ROS区域
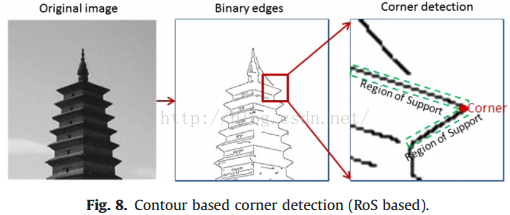
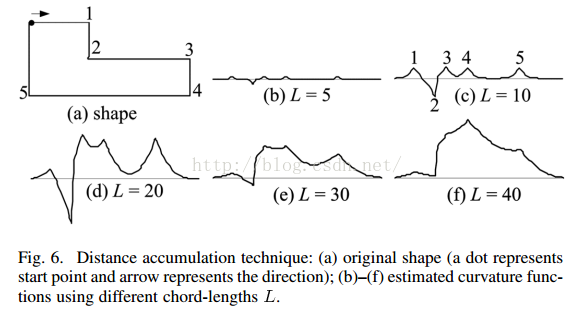
要计算曲线曲度，我们通常都利用一个合适ROS区域，而这个区域的大小将极大的影响我们如何分辨角点。如下图所示，曲线上有5个被标记的点，每个点都是局部最大值，被视为角点候选，如果一个非常小的ROS，所以点都被认为是角点（比如使用CSS或CPDA方法），而如果是非常大的角点，那么2，3，4可能会被认为是错误的角点。当特征的大小没有预先知道，那么找到合适的角点将成会一个问题。
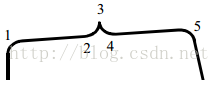
通过这样一种迭代的动态ROS方法，我们最终收敛到合适的角点位置。
判断角度：
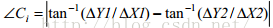
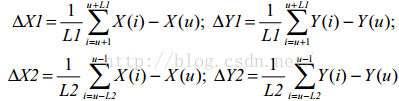
因为角点候选在这个过程中可能会发生改变，随着迭代的进行，其会慢慢收敛，通过这个方法，一些孤立的角点候选会被移除，而一些主要的角点区域将会保留
一般情况下，如果
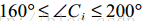，我们可以认为这是一个错误的角点，并将其排除在下次迭代角点候选外。
七、选择出合适的角点
选择出合适的角点的方法一般是采用非极大值抑制，不过，这里还值得一提的就是，基于小波的角点检测方法，其主要是通过上面计算边缘上每点和其对应的角度，将其张成一维曲线，然后对这个曲线进行小波变换，通过比较小波系数来确定角点位置。
另外还有一种非常新奇的方式是通过多尺度下的曲线角度乘积项来确定角点的，由于在细的尺度下，会增加许多细节，而在粗尺度下，这些细节地方会被平滑，所以这些位置的角度将非常小，所以乘积项将会极大减少噪声，而保留角点（其在粗细尺度都要较大）。而在定位角点精确位置时，则不需要对粗尺度下追踪到细尺度了，直接在细尺度下计算该位置就可以了。
参考文献
[1]A Simple and Efficient Algorithm for Detection of High Curvature Points in Planar Curves
[2]Corner detection and curve representation using cubic B-spline
[3]Boundary-based corner detection using eigenvalues of covariance matrices
[4]Robust Image Corner Detection Based on the Chord-to-Point Distance Accumulation Technique
[5]Curvature Scale Space Corner Detector with Adaptive Threshold and Dynamic Region of Support
[6]Wavelet-based corner detection using eigenvectors of covariance matrices
[7] Multi-scale curvature product for robust image corner detection in curvature scale space