图灵机
是什么?
- 图灵机的定义:图灵机本质是可计算的数学模型,也可以成为计算模型
- 图灵机逻辑组成部分:
- 1.无限长度由等份存储数字格子的存储带
- 2.控制器,每次只可读写任意一个存储格中的数据
- 3.状态码,(有限状态,无限状态)
- 4.指令集合,可以称之为程序语句集合,程序都可以
图灵机模型图示:
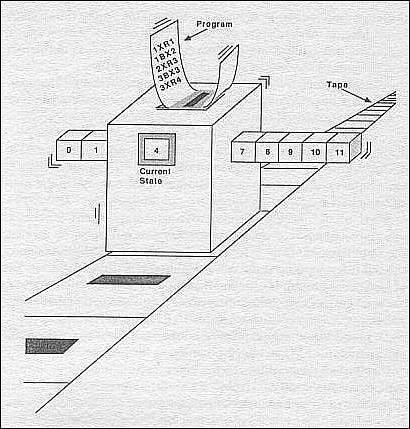
PS:本文中程序语句集合等价于指令集合
为什么?
图灵机解决了什么问题:
先了解一下数学命题,数学所有命题都可以是数学问题,所有的数学命题集合包含可证明的和不可证明的命题。
可证明的数学命题可以通过数理逻辑学抽象建立一个数学模型,数学模型依然抽象所以就需要将数学模型具体为可以计算的计算模型(图灵机),只要计算模型可以计算并且完成计算任务的计算模型都是可计算的模型,逻辑链向上推理这个数学模型就是可以计算的有结果的也是有解的数学模型进而推断出这个数据命题是可证明的。
所以图灵机就是数学模型对应的计算模型,寻找数据模型的可计算模型就是寻找数学模型的图灵机
结论:图灵机是一种概念思想,其解决了判定可计算命题的数学问题
实现验证过程:数学命题->数学模型->计算模型
论证过程:计算结果->数学模型->数学命题
怎么办?
图灵机的工作原理流程:
1.初始化,初始化读写头在存储带的位置和初始化状态码
2.读写头读取存储带数据
2.依据当前状态码和读取的数据在程序指令集合中找到对应的指令
3.执行指令回写数据
5.执行指令的移动控制器命令到读写位置
6.执行指令转入程序指令定义的新状态码
7.回到第2步骤循环继续
图灵机停机:当图灵机的指令执行到无限循环的阶段,那么图灵机就是成功停机
应用例子
条件:
PS:本节内容的索引是我个人为了方便理解记忆的辅助工具,图灵机中没有索引的概念
- 数据带:
| 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 |
|---|---|---|---|---|---|---|---|
| 1 | 1 | 1 | 1 | 0 | 1 | 1 | 1 |
状态码:有限状态码
| 0 | 1 | 2 |
|---|---|---|
| S1 | S2 | S3 |
程序指令集合:
| 索引 | (执行)状态码 | 读值 | 写值 | 动作 | (转入)状态码 |
|---|---|---|---|---|---|
| 0 | S1 | 1 | 1 | R | S1 |
| 1 | S1 | 0 | 1 | R | S2 |
| 2 | S2 | 1 | 1 | R | S2 |
| 3 | S2 | 0 | 0 | L | S3 |
| 4 | S3 | 1 | 0 | H | S3 |
| 5 | S3 | 0 | 0 | H | S3 |
执行步骤说明:
1.初始化:初始化读写头位置的数据带0的位置,初始化状态码S1
2.执行:读取索引0的数据1和依据当前状态码S1找到程序指令集合索引为0的指令执行写入数据1然后读写头右移一位最后状态码转入S1
程序指令的执行流程解析:以索引为0的指令为例
| 1读取数据 | 2当前状态码 | 3写入数据 | 4读写头位移 | 5转入状态码 |
|---|---|---|---|---|
| 1 | S1 | 1 | 读写头右移(移动到数据带位置1) | S1 |
3.重复执行2
4.直到无限逻辑循环后,即为图灵机成功停机
上面的指令和数据带实现了4+3的加法程序,可以自己走完全部流程试一试
拓展
- http://aturingmachine.com/index.php