N皇后经典回溯算法

N皇后题目：
给你一个N*N的棋盘，放置N个皇后，让皇后之间不攻击；攻击规则：皇后可攻击同行、同列、对角线上的所有皇后。

题目分析：如果没有对角线限制，那么这道题就是一个全排列（本人一篇全排列文章：https://blog.csdn.net/u012093557/article/details/107336803）
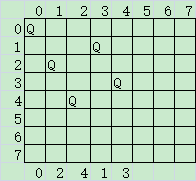
加上对角线限制后，就有很多格子不能放皇后。判断对角线，和同行同列能不能放置，还不是这道题的精髓，这道题的精髓是，前面的都可以，后面发现没法有效放置N个，如何去检验从那一步开始放置错误了。以经典的8皇后为例，如下图所示：
在这里插入图片描述

到第5列时，0-4行都已经有了，[5,5] [6,5] [7,5]分别有对角线冲突，第5行不能放置，就违反了放置8个的可能。那么此次放置不正确，那我们如何知道哪一个放错了呢，我们回退到第4列，第4列只有一个[7,4]的位置可以放置。我们继续往下走，再判断第5列的可能放置。

最后代码实现如下：

// 同行判断是否已经有皇后
bool contain(const vector<int>& vec,int num)
{
    vector<int>::const_iterator iter = find(vec.begin(),vec.end(),num);
    return iter != vec.end();
}

// 斜对角判断是否已经有皇后 des为1.表示判断左下角方向，-1表示判断左上角方向
// 一直要判断到第0列无对角遇到皇后，才算此位置安全。
bool contain(const vector<int>& vec,int column,int row,int des)
{
    if (column >= 0 )
    {
       bool find = false;
       if (column < vec.size() )
       {
         find =  (vec.at(column) == row) ;
       }
       return  find || (contain(vec,column - 1,row + des,des));
    }
    return false;
}

// 打印一组皇后组合
void printList(const vector<int>& nums)
{
    printf("\n");
    for (int j = 0; j < nums.size(); j++)
    {
        printf("%d\t",nums.at(j));
    }
}

void findNext(vector<int>& nums,int column,const int count)
{
    for (int row = 0; row < count && column < count; row++)
    {
        if (!contain(nums,row) //同行查询：nums列表中无数字是row行；因为是按照列每列选择，那么不比对列，
                && !contain(nums,column,row, -1)  // 左上对角线是否有皇后
                && !contain(nums,column,row, 1) ) // 左下对角线是否有皇后
        {
            nums.push_back(row);
            if ((nums.size() == (column + 1)) && (nums.size() == count))
            {
               printList(nums);
            }
            findNext(nums,column + 1,count);
            nums.pop_back();   // 回退
        }
    }
}

int main(int argc, char *argv[])
{
    int n = 8;      // 以8皇后为例
    vector<int> nums;
    findNext(nums,0,n);
    printf("\n");
    return 0;
}

8皇后的打印结果共92组：
0 4 7 5 2 6 1 3
0 5 7 2 6 3 1 4
0 6 3 5 7 1 4 2
0 6 4 7 1 3 5 2
1 3 5 7 2 0 6 4
1 4 6 0 2 7 5 3
1 4 6 3 0 7 5 2
1 5 0 6 3 7 2 4
1 5 7 2 0 3 6 4
1 6 2 5 7 4 0 3
1 6 4 7 0 3 5 2
1 7 5 0 2 4 6 3
2 0 6 4 7 1 3 5
2 4 1 7 0 6 3 5
2 4 1 7 5 3 6 0
2 4 6 0 3 1 7 5
2 4 7 3 0 6 1 5
2 5 1 4 7 0 6 3
2 5 1 6 0 3 7 4
2 5 1 6 4 0 7 3
2 5 3 0 7 4 6 1
2 5 3 1 7 4 6 0
2 5 7 0 3 6 4 1
2 5 7 0 4 6 1 3
2 5 7 1 3 0 6 4
2 6 1 7 4 0 3 5
2 6 1 7 5 3 0 4
2 7 3 6 0 5 1 4
3 0 4 7 1 6 2 5
3 0 4 7 5 2 6 1
3 1 4 7 5 0 2 6
3 1 6 2 5 7 0 4
3 1 6 2 5 7 4 0
3 1 6 4 0 7 5 2
3 1 7 4 6 0 2 5
3 1 7 5 0 2 4 6
3 5 0 4 1 7 2 6
3 5 7 1 6 0 2 4
3 5 7 2 0 6 4 1
3 6 0 7 4 1 5 2
3 6 2 7 1 4 0 5
3 6 4 1 5 0 2 7
3 6 4 2 0 5 7 1
3 7 0 2 5 1 6 4
3 7 0 4 6 1 5 2
3 7 4 2 0 6 1 5
4 0 3 5 7 1 6 2
4 0 7 3 1 6 2 5
4 0 7 5 2 6 1 3
4 1 3 5 7 2 0 6
4 1 3 6 2 7 5 0
4 1 5 0 6 3 7 2
4 1 7 0 3 6 2 5
4 2 0 5 7 1 3 6
4 2 0 6 1 7 5 3
4 2 7 3 6 0 5 1
4 6 0 2 7 5 3 1
4 6 0 3 1 7 5 2
4 6 1 3 7 0 2 5
4 6 1 5 2 0 3 7
4 6 1 5 2 0 7 3
4 6 3 0 2 7 5 1
4 7 3 0 2 5 1 6
4 7 3 0 6 1 5 2
5 0 4 1 7 2 6 3
5 1 6 0 2 4 7 3
5 1 6 0 3 7 4 2
5 2 0 6 4 7 1 3
5 2 0 7 3 1 6 4
5 2 0 7 4 1 3 6
5 2 4 6 0 3 1 7
5 2 4 7 0 3 1 6
5 2 6 1 3 7 0 4
5 2 6 1 7 4 0 3
5 2 6 3 0 7 1 4
5 3 0 4 7 1 6 2
5 3 1 7 4 6 0 2
5 3 6 0 2 4 1 7
5 3 6 0 7 1 4 2
5 7 1 3 0 6 4 2
6 0 2 7 5 3 1 4
6 1 3 0 7 4 2 5
6 1 5 2 0 3 7 4
6 2 0 5 7 4 1 3
6 2 7 1 4 0 5 3
6 3 1 4 7 0 2 5
6 3 1 7 5 0 2 4
6 4 2 0 5 7 1 3
7 1 3 0 6 4 2 5
7 1 4 2 0 6 3 5
7 2 0 5 1 4 6 3
7 3 0 2 5 1 6 4

N皇后经典回溯算法

悦读