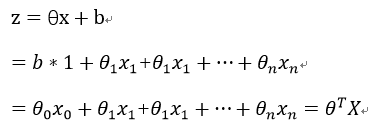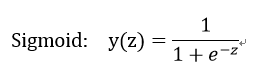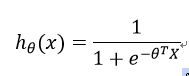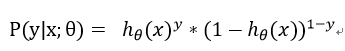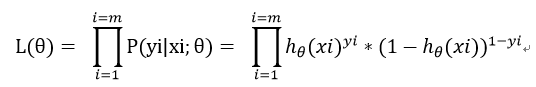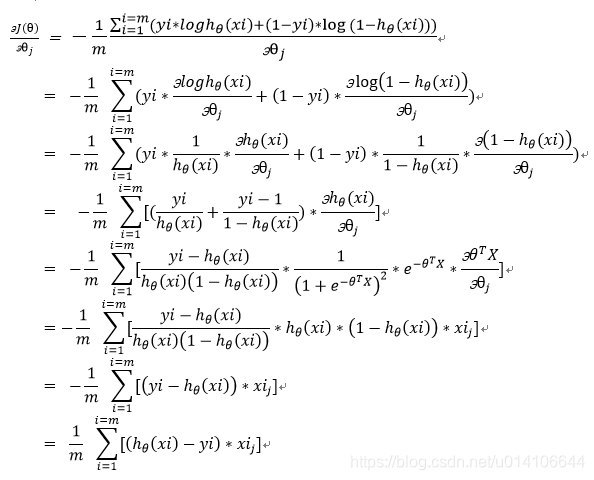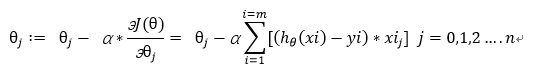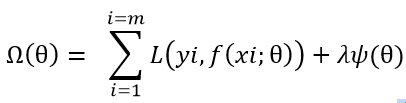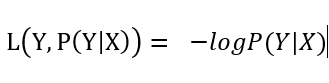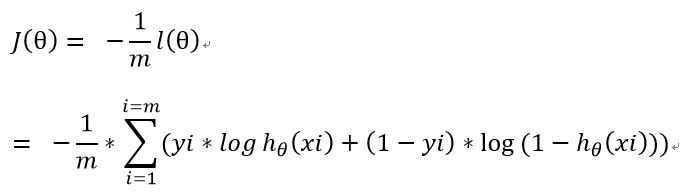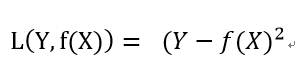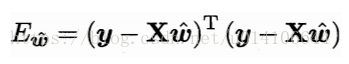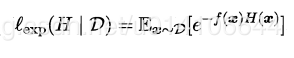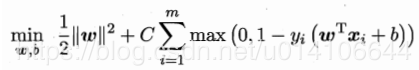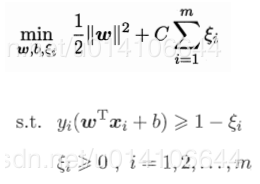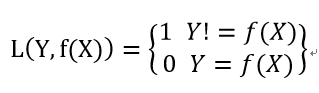今天第一次算法面试，被问到了LR回归，没有实践经验有些问题还是理解不到位，现在总结一下。

1.LR的推导

LR逻辑回归是一种监督学习分类算法，其实现了给定数据集到0,1的一种映射。

给定数据集其中（xi,yi）表示第i个样本，其中。即每个数据有n个特征，类别，要求训练数据，将数据分成两类0或1。

假定xi的n个特征为线性关系，即：

这里为了表示简洁，在数据样本xi添加一个特征x0=1  将b作为。则有：

以上实现了用样本xi的n个特征来表示样本的表达式，现在需要寻找一个映射使得z可以转换为0或者1。

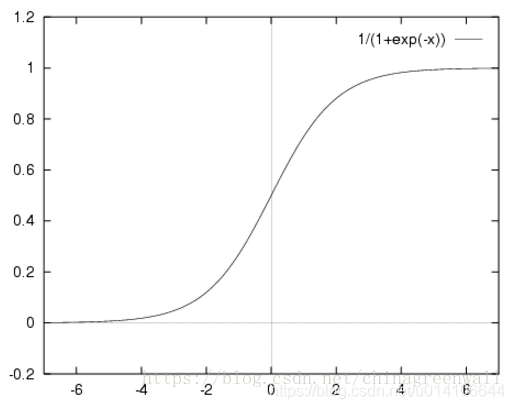
可以使用阶跃函数，但是阶跃函数性质不好，不可导求解过于复杂，这里选用Sigmoid函数:

当输入一个Z时，y输出一个0--1之间的数，假定y>0.5则最终结果判为1  y<0.5最终结果为0。当y=0.8时，最终结果为1,y=0.8也表征了此时输出为1的概率，令：

将样本特征线性表示，然后输入到Sigmoid函数，输出结果在0--1之间，并且输出结果表征了分类结果为1的概率，即有：

即输出刚好代表了结果为1的概率

LR逻辑回归假设样本服从泊松0--1分布，因此p(y|x)表达式：

假设样本独立且同分布，最大似然估计：

进而求最大对数似然估计：

第一个问题，为什么要求最大对数似然估计而不是最大似然估计：

第二个问题，LR的损失函数是什么：

损失函数表征预测值与真实值之间的差异程度，如果预测值与真实值越接近则损失函数应该越小。在此损失函数可以取为最大似然估计函数的相反数，其次除以m这一因子并不改变最终求导极值结果，通过除以m可以得到平均损失值，避免样本数量对于损失值的影响。

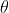
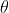
这里采用随机梯度下降，损失函数对于j偏导：

j的迭代式：

2.损失函数

损失函数：表征模型预测值与真实值的不一致程度。记为函数L(Y，f(X))

结构风险函数 = 经验风险项  +  正则项  其中损失函数为经验风险项的重要组成部分

前半部分为经验风险项，后半部分为正则项。

1.对数损失函数：

P(Y|X)为样本为Y的概率，数值越大说明预测值与真实值越接近即损失函数应该越小，当P（Y|X）越大的，-logP(Y|X)越小，刚好符合损失函数的定义。

其中LR逻辑回归损失函数即为对数损失函数：

逻辑回归假设样本服从伯努利分布（0-1分布），然后求得满足该分布的似然函数，接着取对数求极值最小化负的似然函数（即max F(y, f(x)) —-> min -F(y, f(x)))

即LR的损失函数为： 负的对数损失函数：

2.平方损失函数

线性回归模型使用了平方损失函数：

在线性回归中，它假设样本和噪声都服从高斯分布（中心极限定理），最后通过极大似然估计（MLE）可以推导出最小二乘式子。

3.指数损失函数

AdaBoost中损失函数为：

4.Hinge损失函数

f(x)如果与y一致，则损失函数为0，不一致则损失函数为w（y）y的有关函数

SVM中损失函数即为Hinge损失函数：

进而变形为：

5. 0-1损失函数

6.绝对值损失函数

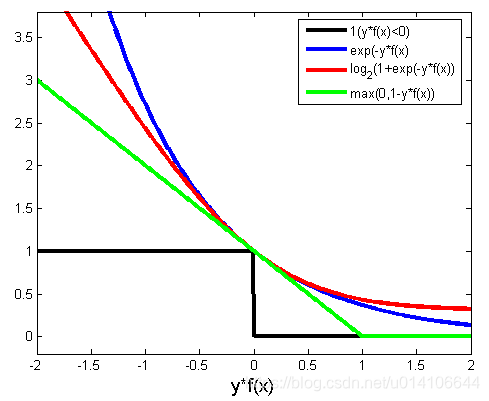
各种损失函数：

参考链接：

https://www.cnblogs.com/shixiangwan/p/7953591.html