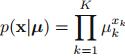第二章主要介绍几个重要的概率分布及其特性。
1. 二值变量的概率分布
假设一个二元随机变量 ,用参数
,用参数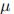 表示
表示 的概率为:
的概率为: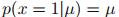 。
。
 ,用参数
,用参数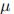 表示
表示 的概率为:
的概率为: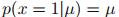 。
。
(1)伯努利分布(Bernoulli distribution)
概率分布函数:
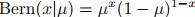
期望:
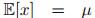
方差:
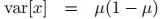
log似然函数为:
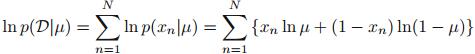
其中,![]()
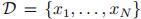 表示变量x的观测值。得到
表示变量x的观测值。得到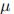 的最大似然估计值为:
的最大似然估计值为:
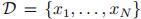 表示变量x的观测值。得到
表示变量x的观测值。得到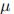 的最大似然估计值为:
的最大似然估计值为:
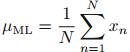
(2)二项分布(Binomial distribution)
概率分布函数:
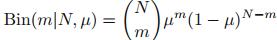 ,
,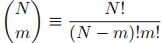
期望:
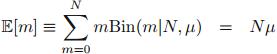
方差:
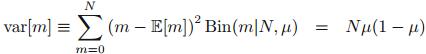
注:对于小的数据集,如果对二项分布采用极大似然估计,会得到过拟合(over-fitting)的估计结果。可以采用贝叶斯方法,引入共轭先验分布(conjugate prior distribution)来解决这个问题。共轭先验是指,选取一个与似然函数共轭的先验分布,使得后验分布与先验分布有同样的函数形式。其中,二项分布的共轭先验是Beta分布。
(3)Beta分布
概率分布函数:
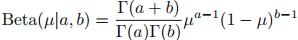
期望:
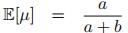
方差:
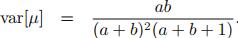
采用贝叶斯方法,将Beta先验乘以二项分布似然函数,得到后验分布如下:
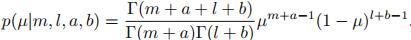
2. 多项式变量的概率分布
多项式变量可以取多种结果中的一种,而二值变量只能取两种结果中的一种。假设变量x可以取K=6种结果,若x的某一次观测值为第三种结果(![]()
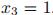 ),则可以将x表示为
),则可以将x表示为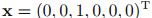
![]() 。另外,用参数
。另外,用参数![]()
 表示
表示![]()
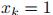 的概率:
的概率:![]()
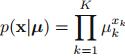
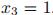 ),则可以将x表示为
),则可以将x表示为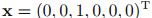
 表示
表示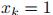 的概率:
的概率: