分治法的设计思想是：将一个难以直接解决的大问题，分割成一些规模较小的相同问题，以便各个击破，分而治之。

  分治法所能解决的问题一般具有以下几个特征：

• 该问题的规模缩小到一定的程度就可以容易地解决
• 该问题可以分解为若干个规模较小的相同问题，即该问题具有最优子结构性质。
• 利用该问题分解出的子问题的解可以合并为该问题的解；
• 该问题所分解出的各个子问题是相互独立的，即子问题之间不包含公共的子子问题。

  第三条特征是关键，能否利用分治法完全取决于问题是否具有第三条特征，如果具备了第一条和第二条特征，而不具备第三条特征，则可以考虑用贪心法或动态规划法。

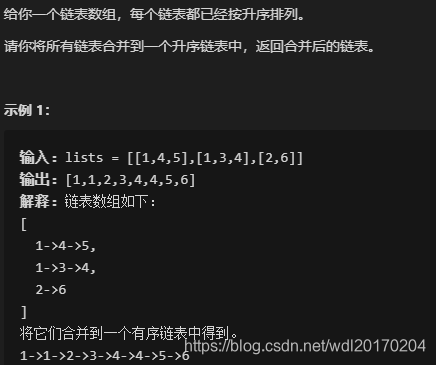
leetcode23：合并K个升序链表

思路：

1. 要合并k个链表，可以参考合并两个链表。
2. 可以每次把k个链表分组，递归，直至只剩两个链表或一个链表。
3. 合并两个链表后，递归上升，规模减少二分之一，依次合并。

代码如下：

class Solution
{
public:
    ListNode *merageTwoLists(ListNode *a, ListNode *b)
    {
        if (a == nullptr || b == nullptr)
            return a == nullptr ? b : a;

        ListNode *pa = a;
        ListNode *pb = b;

        ListNode *ans = new ListNode();
        ListNode *p = ans;

        while (pa != nullptr && pb != nullptr)
        {
            if (pa->val < pb->val)
            {
                p->next = pa;
                pa = pa->next;
            }
            else
            {
                p->next = pb;
                pb = pb->next;
            }

            p = p->next;
        }

        p->next = (pa == nullptr) ? pb : pa;
        return ans->next;
    }

    ListNode *merge(vector<ListNode *> &lists, int l, int r)
    {
        if (l == r)
            return lists[l];
        if (l > r)
            return nullptr;
        int mid = (l + r) >> 1;
        return merageTwoLists(merge(lists, l, mid), merge(lists, mid + 1, r));
    }

    ListNode* mergeKLists(vector<ListNode*>& lists) {
        return merge(lists, 0, lists.size() - 1);
    }
};

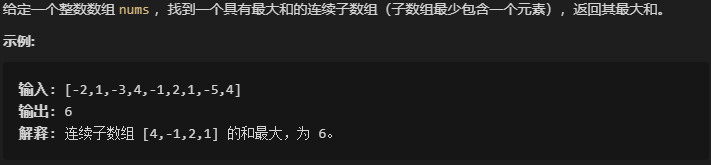
leetcode53：最大子序和

注：以下思路参考了leetcode官方题解思路，附以个人理解。
思路如下：

1. 首先将数组分为两部分，[L,mid]、[mid+1,R]。
2. 维护四个变量：LSum 表示 [L,R] 内以 L为左端点的最大子段和，rSum 表示 [L,R] 内以 R为右端点的最大子段和，mSum 表示 [L,R] 内的最大子段和，iSum 表示[L,R] 的区间和。
3. iSum很好求，直接就是左区间iSum+右区间iSum。
4. 对于LSum，存在两种可能，它要么等于左区间的 LSum，要么等于左区间的 iSum 加上右区间的 LSum，二者取大。
5. 对于RSum，要么等于左区间的 RSum，要么等于右区间的 iSum 加上左区间的 RSum，二者取大。
6. 对于mSum，它可能是LSum，也可能是RSum，也可能是LSum+RSum。

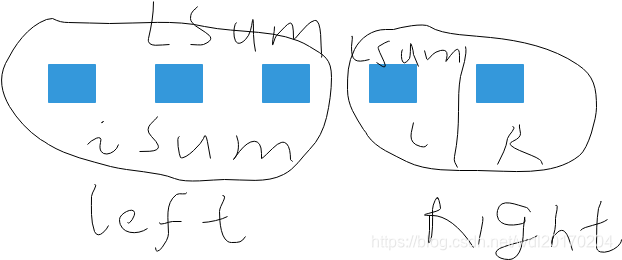
在以上思路中，第4、5步不是很好理解，以LSum为例，如下图所示：

  上面是一个简单图示，从图中可以看出，如果最大子序和以区间左端点开始，那么要么是左区间LSum,如果跨越中点，就只能是iSum+有区间的LSum。
  代码如下：

class Solution {
public:
    struct Status {
        int lSum, rSum, mSum, iSum;
    };

    Status pushUp(Status l, Status r) {
        int iSum = l.iSum + r.iSum;
        int lSum = max(l.lSum, l.iSum + r.lSum);
        int rSum = max(r.rSum, r.iSum + l.rSum);
        int mSum = max(max(l.mSum, r.mSum), l.rSum + r.lSum);
        return (Status) {lSum, rSum, mSum, iSum};
    };

    Status get(vector<int> &a, int l, int r) {
        if (l == r) {
            return (Status) {a[l], a[l], a[l], a[l]};
        }
        int m = (l + r) >> 1;
        Status lSub = get(a, l, m);
        Status rSub = get(a, m + 1, r);
        return pushUp(lSub, rSub);
    }

    int maxSubArray(vector<int>& nums) {
        return get(nums, 0, nums.size() - 1).mSum;
    }
};

  从上面这些题目中我们可以看到分治算法的一些特点，简单而言，也就是分而治之，把问题不断分解，直到分解为可以容易解决的规模。除了这道题以外，最典型的分治算法还有二分查找、快速排序。