---内容开始---
这是一份编译原理实验报告,分析表是手动造的,可以作为借鉴。
基于 SLR(1) 分析法的语法制导翻译及中间代码生成程序设计原理与实现
1 、理论传授
语法制导的基本概念,目标代码结构分析的基本方法,赋值语句语法制导生成四元式的
基本原理和方法,该过程包括语法分析和语义分析过程。
2 、目标任务
[ 实验 项目] 完成以下描述赋值语句 SLR(1)文法语法制导生成中间代码四元式的过程。
G[A]:A→V=E
E→E+T∣E-T∣T
T→T*F∣T/F∣F
F→(E)∣i
V→i
[ 设计说明 ] 终结符号 i 为用户定义的简单变量,即标识符的定义。
[ 设计要求]
(1)构造文法的 SLR(1)分析表,设计语法制导翻译过程,给出每一产生式
对应的语义动作;
(2)设计中间代码四元式的结构;
(3)输入串应是词法分析的输出二元式序列,即某赋值语句“专题 1”的输出结果,输出为赋值语句的四元式序列中间文件;
(4)设计两个测试用例(尽可能完备),并给出程序执行结果四元式序列。
3、 程序功能描述
在第一次实验词法分析输出结果的基础上设计SLR1文法分析过程,并了解四元式的形成:
- 输入串为实验一的二元式序列
- 输出为对输入串的SLR(1)文法的判断结果
- 输出有针对输入串的SLR(1)文法的具体分析过程
- 有对输入串的四元式输出序列
4、 主要数据结构描述
二元组结构体,用来存储词法分析程序输出的二元组对 <类别,单词>:
int count;
struct eryuanzu
{
int a;
char temp[COUNT];
}m[COUNT];
void out(int a,char* temp){// 打印二元组
printf("< %d %s >\n",a,temp);
m[count].a=a;
strcpy(m[count].temp,temp); //
count++;
}
SLR1分析过程中所要用到的状态栈、符号栈等:
stack<int> state; //状态栈
stack<char> sign; //符号栈
char st; //规约弹出时,状态栈顶元素
int flag=0; //标志是否是SLR
stack<string> place; //变量地址栈
ACTION表,二维数组表示:
/* i ( ) + - * / = #
以1开头的百位数为s移进项,0为error,-1为accept,其余的一位两位数是r规约项*/
int ACTION[20][9]={ {103,0,0,0,0,0,0,0,0},//0
{0,0,0,0,0,0,0,0,-1},
{0,0,0,0,0,0,0,104,0},
{0,0,0,0,0,0,0,10,0},
{109,108,0,0,0,0,0,0},
{0,0,0,110,111,0,0,0,1},//5 mnl;;huhyhjhjio
{0,0,4,4,4,112,113,0,4},
{0,0,7,7,7,7,7,0,7},
{109,108,0,0,0,0,0,0,0},
{0,0,9,9,9,9,9,0,9},
{109,108,0,0,0,0,0,0,0},//10
{109,108,0,0,0,0,0,0,0},
{109,108,0,0,0,0,0,0,0},
{109,108,0,0,0,0,0,0,0},
{0,0,119,110,111,0,0,0,0},
{0,0,2,2,2,112,113,0,2},//
{0,0,3,3,3,112,113,0,3},
{0,0,5,5,5,5,5,0,5},
{0,0,6,6,6,6,6,0,6},
{0,0,8,8,8,8,8,0,8}};//19
·GOTO表,二维数组表示:
//A V E T F
int GOTO[20][5]={ {1,2,0,0,0},
{0,0,0,0,0},//1
{0,0,0,0,0},
{0,0,0,0,0},
{0,0,5,6,7},
{0,0,0,0,0},//5
{0,0,0,0,0},
{0,0,0,0,0},
{0,0,14,6,7},
{0,0,0,15,7},
{0,0,0,16,7},//10
{0,0,0,0,17},
{0,0,0,0,18},
{0,0,0,0,0},
{0,0,0,0,0},
{0,0,0,0,0},//15
{0,0,0,0,0},
{0,0,0,0,0},
{0,0,0,0,0},
{0,0,0,0,0}};//19
规约时所用到的函数,分别对应每一条规则:
void R1(); //A→V=E
void R2(); //E→E+T
void R3(); //E→E-T
void R4(); //E→T
void R5(); //T→T*F
void R6(); //T→T/F
void R7(); //T→F
void R8(); //F→(E)
void R9(); //F→i
void R10(); //V→i
void R1() {
sign.pop(); sign.pop(); sign.pop(); //弹出符号栈
state.pop(); state.pop(); state.pop(); //弹出状态栈
sign.push('A'); //符号'A'入栈
st=state.top();
printf("r1\t");
}
void R2() {
sign.pop(); sign.pop(); sign.pop(); //弹出符号栈
state.pop(); state.pop(); state.pop(); //弹出状态栈
sign.push('E'); st=state.top(); //符号'E'入栈
printf("r2\t\t");
}
void R3() {
sign.pop(); sign.pop(); sign.pop();
state.pop(); state.pop(); state.pop();
sign.push('E');st=state.top();
printf("r3\t\t");
}
void R4() {
sign.pop();
state.pop();
sign.push('E');st=state.top();
printf("r4\t\t");
}
void R5() {
sign.pop(); sign.pop(); sign.pop();
state.pop(); state.pop(); state.pop();
sign.push('T');st=state.top();
printf("r5\t\t");
}
void R6() {
sign.pop(); sign.pop(); sign.pop();
state.pop(); state.pop(); state.pop();
sign.push('T');st=state.top();
printf("r6\t\t");
}
void R7() {
sign.pop();
state.pop();
sign.push('T');st=state.top();
printf("r7\t\t");
}
void R8() {
sign.pop(); sign.pop(); sign.pop();
state.pop(); state.pop(); state.pop();
sign.push('F');st=state.top();
printf("r8\t\t");
}
void R9() {
sign.pop();
state.pop();
sign.push('F');st=state.top();
printf("r9\t\t");
}
void R10() {
sign.pop();
state.pop();
sign.push('V');st=state.top();
printf("r10\t\t");
}
SLR1分析处理函数:
void SLR()
{
printf("输入串\t\t状态栈\t\t符号栈\t\tACTION\t\tGOTO ");
int i,j,k=1;
state.push(0); //初始化
sign.push('#');
int which; //对应表项内容
char c; //输入符号串首
int a; //坐标
int b;
do{
printf("\n");
c=m[k-1].temp[0]; //输入符号串首
cout<<c<<' ';
for(int j=k;j<=count;j++)
printf("%s",m[j].temp);
printf("\t\t");
displayStack(state);
displayStack1(sign);
a=state.top(); //坐标
b=isVt(c);
/*if(isOp(c)!=-1)
temp1=c;
place.push(temp1);*/
if(b!=-1) //输入串首c是终结符
{
which=ACTION[a][b];
if(which==-1)
{
printf(" acc,分析成功!\n");
flag=1;
break;
}
else if(which==0)
{ printf("error项1\n ");break; }
else if(which>=100) //移进
{
which=s_r(which);
printf("s%d\t\t",which);
sign.push(c);
state.push(which);
k++;
}
else
{
switch(which) //which整型,case不要加''
{
case 1:R1();break;
case 2:R2();break;
case 3:R3();break;
case 4:R4();break;
case 5:R5();break;
case 6:R6();break;
case 7:R7();break;
case 8:R8();break;
case 9:R9();break;
case 10:R10();break;
default:printf("which=%derror项2\n ");break;
}
//状态转移 Vn
int e=isVn(sign.top());
if(e!=-1)
{
int convert=GOTO[st][e];
state.push(convert);
printf("GOTO[%d,%c]=%d",st,sign.top(),convert);
}
}
}
else
{ printf("error_b ");break; }
}while(which!=-1);//while
}
5、实验测试
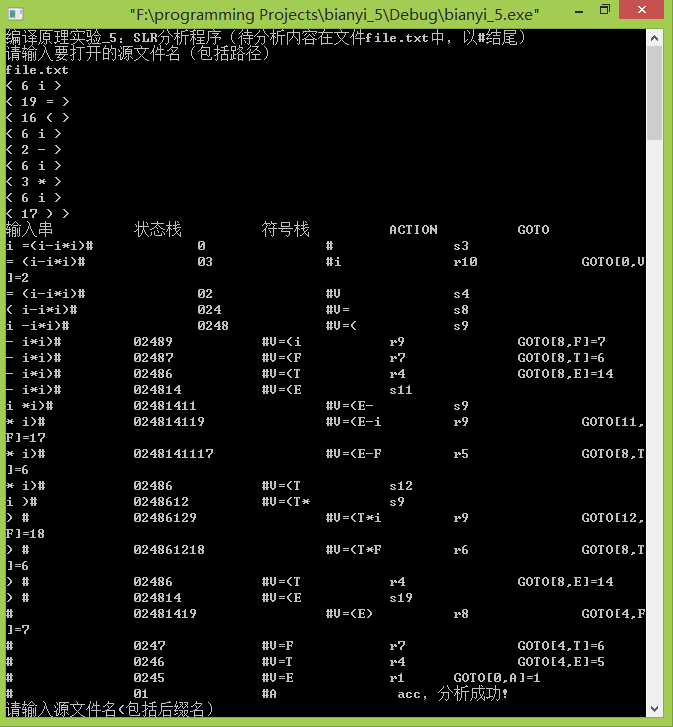
1.测试用例:i=(i-i*i)#,输入file.txt直接从文件读取输入串,得到结果如下:
四元式结果输出:
由于图片无法上传便罢
6、 实验总结
本次实验是对理论课上所学知识的应用,重点是理解分析栈和符号栈,这里我采用自行造ACTION和GOTO表,这样SLR分析表就出来了,自动造表还是比较复杂。而且在造表的过程中经常出错,最后在大家的讨论中解决了。造完表后的分析过程并不复杂,按部就班分情况来处理。
本次实验加深了我对SLR1的分析过程的理解,也加深了对四元式的认识。
7、源代码
分为两个CPP
Siyuanshi.cpp
#include "stdafx.h" #include<stdlib.h> #include<fstream> #include<iostream> #include<stdio.h> using namespace std; #define MAX 100 int mm=0,sum=0;//sum用于计算运算符的个数 //mm用于标输入表达式中字符的个数 char JG='A'; char str[MAX];//用于存输入表达式 int token=0;//左括号的标志 /***********用于更改计算后数组中的值**************/ void change(int e) { int f=e+