线索二叉树 - 悦读

线索二叉树 (threaded binary tree)

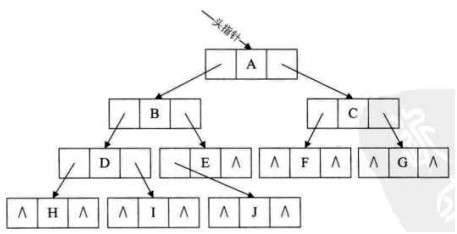
上图所示的二叉链表，存在多个空指针域。假设一个二叉链表的结点数为n，则共有2n个指针域。而n个结点的二叉树共有n-1条分支。所以空指针域的个数为：2n - (n-1) = n+1。

可以在这n+1个空指针域中保存结点的（以先序、中序或后序遍历的）前驱和后继指针，这样在下次遍历时，可以大大提高速度。

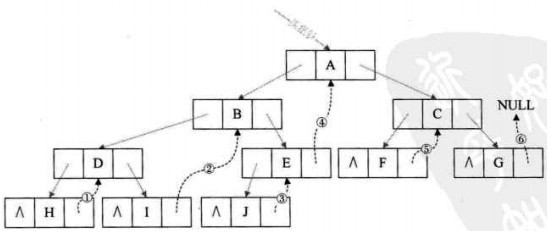
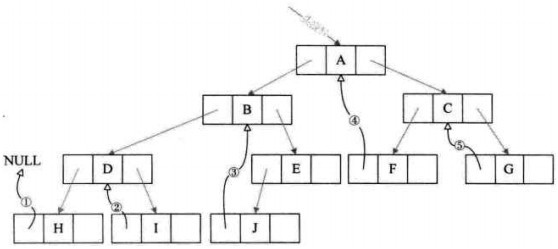
将所有空指针域中的rchild指向它的后继。

将所有空指针域中的lchild指向它的前驱。

线索二叉树(保留遍历时结点在任一串行的前驱和后继的信息)：若结点有左子树，则其lchild域指示其左孩子，否则令lchild域指示其前驱；若结点有右子树，则其rchild域指示其右孩子，否则令rchild指示其后继。

还需在结点结构中增加两个标志域LTag和RTag。LTag=0时，lchild域指示结点的左孩子，LTag=1时，lchild域指示结点的前驱；RTag=0时，rchild域指示结点的右孩子，RTag=1时，rchild域指示结点的后继。

以这种结点结构构成的二叉链表作为二叉树的存储结构，叫做线索链表，其中指向结点前驱和后继的指针叫做线索，加上线索的二叉树称为线索二叉树。对二叉树以某种次序遍历使其变为线索二叉树的过程叫做线索化。若对二叉树进行中序遍历，则所得的线索二叉树称为中序线索二叉树，线索链表称为为中序线索链表。

二叉线索存储表示

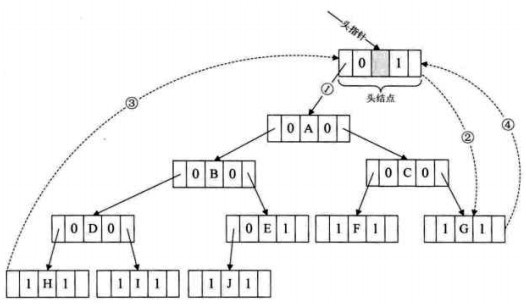
二叉树的二叉线索存储表示（以中序为例）：在线索链表上添加一个头结点，并令其lchild域的指针指向二叉树的根结点，其rchild域的指针指向中序遍历时访问的最后一个结点。令二叉树中序串行中的第一个结点的lchild域指针和最后一个结点的rchild域的指针均指向头结点，这样就创建了一个双向线索链表。这样定义的好处是既可以从第一个结点起顺后继进行遍历，也可以从最后一个结点起顺前驱进行遍历。

/* 二叉树的二叉线索存储表示 */
 typedef enum{Link,Thread}PointerTag; /* Link(0)：指针，Thread(1)：线索 */
 typedef struct BiThrNode
 {
   TElemType data;
   struct BiThrNode *lchild,*rchild; /* 左右孩子指针 */
   PointerTag LTag,RTag; /* 左右标志 */
 }BiThrNode,*BiThrTree;

中序遍历线索化的递归函数如下：

BiThrTree pre; /* 全局变量，始终指向刚刚访问过的结点 */
 void InThreading(BiThrTree p)
 { /* 通过中序遍历进行中序线索化，线索化之后pre指向最后一个结点。*/
   if(p) /* 线索二叉树不空 */
   {
     InThreading(p->lchild); /* 递归左子树线索化 */

     if(!p->lchild) /* 没有左孩子 */
     {
       p->LTag=Thread; /* 左标志为线索(前驱) */
       p->lchild=pre; /* 左孩子指针指向前驱 */
     }

     if(!pre->rchild) /* 前驱沒有右孩子 */
     {
       pre->RTag=Thread; /* 前驱的右标志为线索(后继) */
       pre->rchild=p; /* 前驱右孩子指针指向其后继(当前结点p) */
     }

     pre=p; /* 保持pre指向p的前驱 */

     InThreading(p->rchild); /* 递归右子树线索化 */
   }
 }

/* 结合上面的文字介绍和示意图看 */
void InOrderThreading(BiThrTree *Thrt,BiThrTree T)
 { /* 中序遍历二叉树T，并将其中序线索化，Thrt指向头结点。 */
   *Thrt=(BiThrTree)malloc(sizeof(BiThrNode));
   if(!*Thrt) /* 生成头结点不成功 */
     exit(OVERFLOW);
   (*Thrt)->LTag=Link; /* 建头结点，左标志为指针 */
   (*Thrt)->RTag=Thread; /* 右标志为线索 */
   (*Thrt)->rchild=*Thrt; /* 右指针回指 */
   if(!T) /* 若二叉树空，则左指针回指 */
     (*Thrt)->lchild=*Thrt;
   else
   {
     (*Thrt)->lchild=T; /* 头结点的左指针指向根结点 */
     pre=*Thrt; /* pre(前驱)的初值指向头结点 */
     InThreading(T); /* 中序遍历进行中序线索化，pre指向中序遍历的最后一个结点 */
     pre->rchild=*Thrt; /* 最后一个结点的右指针指向头结点 */
     pre->RTag=Thread; /* 最后一个结点的右标志为线索 */
     (*Thrt)->rchild=pre; /* 头结点的右指针指向中序遍历的最后一个结点 */
   }
 }

下面是中序遍历线索二叉树T的非递归算法：

void InOrderTraverse_Thr(BiThrTree T,void(*Visit)(TElemType))
 { /* 中序遍历线索二叉树T(头结点)的非递归算法。*/
   BiThrTree p;
   p=T->lchild; /* p指向根结点 */

   while(p!=T)
   { /* 空树或遍历结束时，p==T */
     while(p->LTag==Link) /* 由根结点一直找到二叉树的最左结点 */
       p=p->lchild;
     Visit(p->data); /* 访问此结点 */

     while(p->RTag==Thread&&p->rchild!=T) /* p->rchild是线索(后继)，且不是遍历的最后一个结点 */
     {
       p=p->rchild;
       Visit(p->data); /* 访问后继结点 */
     }

     p=p->rchild; /* 若p->rchild不是线索(是右孩子)，p指向右孩子，返回循环，*/
   }              /* 找这棵子树中序遍历的第1个结点 */
 }

Reference:

[1] 《大话数据结构》

[2] wikipedia(二叉树)：http://zh.wikipedia.org/wiki/%E4%BA%8C%E5%8F%89%E6%A0%91