一、双S型速度规划解决了梯形加速度曲线不连续的问题
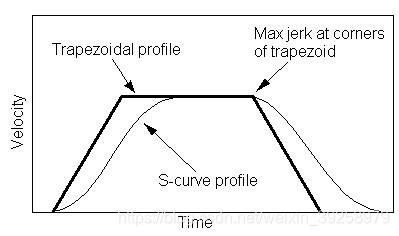
梯形速度规划的加速度曲线是不连续的,这对于系统是有害的。从机械系统的角度来说,不连续的加速度会产生不必要的冲击力,使得机械系统产生抖动甚至破坏。双S型速度规划采用两段线性区间组合的方法解决加速度不连续的问题,线性段端点处采用抛物线过渡的方法,保证连接处的加速度曲线连续。若一个系统能够提供足够大的加加速度,双S型速度规划将会等同于梯形速度规划。另外,在相同的距离和期望速度下,双S型速度规划耗费的时间更多[1],计算也更复杂:
二、双S型速度规划是什么?
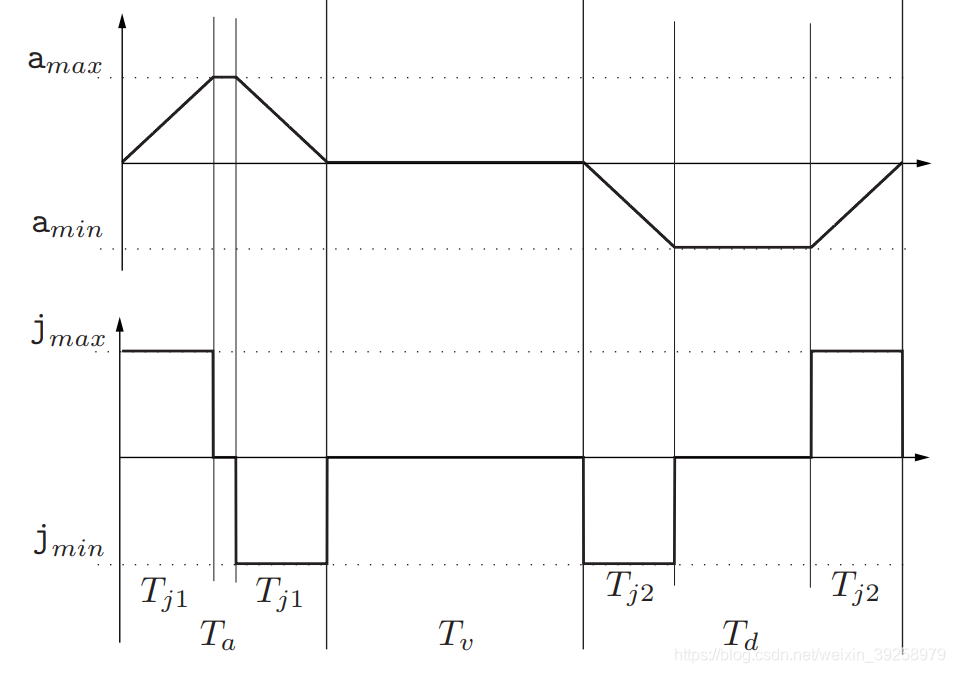
双S型速度规划是一种速度规划方式,其目的是为了减少对机械系统造成的影响。也叫铃型规划(Bell)七段S型速度规划。速度曲线如下图所示:
观察上述速度曲线图,可以将整个运动可分为A M D三个过程,分别是:
- 加速阶段(Acceleration Phase, AP)
- 最大速度阶段(Maximum Phase, MP)
- 减速阶段(Deceleration Phase, DP)
AP段和DP段端点处采用抛物线进行拟合,避免了加速度突变。因为AP DP段速度曲线的形状像英文字母中的“S”所以叫做双S型速度规划,事实上,只要存在一个"S"就能称为S型速度规划。
三、规划参数及各阶段特征、规划基本条件
3.1 规划参数
规划参数是对速度轨迹形状的约束,可分为用户参数和系统参数,其中用户参数一般不作修改,为了达到规定的用户参数,系统参数可能会修调。用户参数指的是起始位置及速度:
- 整个规划端点处位移( q 0 q_0 q0 q 1 q_1 q1)
- 整个规划端点处速度( v 0 v_0 v0 v 1 v_1 v1)
系统参数是指:
- 速度上下限( v m a x v_{max} vmax v m i n v_{min} vmin)
- 最大加速度( a m a x a_{max} amax a m i n a_{min} amin)
- 最大加加速度( j m a x j_{max} jmax j m i n j_{min} jmin)
绝大多数时候,系统参数会采用“对称”规划,即:
j
m
i
n
=
−
j
m
a
x
a
m
i
n
=
−
a
m
a
x
v
m
i
n
=
−
v
m
a
x
(3.1)
j_{min}=-j_{max}\\ a_{min}=-a_{max}\\ v_{min}=-v_{max}\tag{3.1}
jmin=−jmaxamin=−amaxvmin=−vmax(3.1)
文章的讨论都是基于(3.1)的对称规划进行的讨论。
3.2 各阶段的特征
我们先讨论位移增大的情况( q 1 > q 0 q_1>q_0 q1>q0),在文章的最后我们将介绍位移减少情况( q 1 < q 0 q_1<q_0 q1<q0),因为我们规定:
-
t ∈ [ 0 , T a ) t\in[0,T_a) t∈[0,Ta):加速阶段(AP),加速度主要特征是线性变化,大小从 0 → a m a x → 0 0\rightarrow a_{max} \rightarrow 0 0→amax→0;
-
t ∈ [ T a , T a + T v ) t\in[T_a,T_a+T_v) t∈[Ta,Ta+Tv):匀速阶段(MP),速度的特征是大小保持不变;
-
t ∈ [ T a + T v , T ] t\in[T_a+Tv,T] t∈[Ta+Tv,T]:减速阶段(DP),加速度主要特征仍然是线性变化,大小从 0 → a m i n → 0 0\rightarrow a_{min} \rightarrow 0 0→amin→0,其中 T = T a + T v + T d T=T_a+T_v+T_d T=Ta+Tv+Td 。
3.3 规划基本条件
不是所有的规划参数都能进行S型规划,在极限情况下,仅存在单一加速或减速段,也就是一正一负加加速度脉冲。规定至少完成一个“S”曲线为规划基本条件,记S型曲线单个脉冲耗时为 T j ∗ T_j^* Tj∗,根据运行过程中加速度能否到达最大加速度有,分为两种情况:
- T j ∗ = ∣ v 1 − v 0 ∣ j m a x T_j^*=\sqrt{\frac{|v_1-v_0|}{j_{max}}} Tj∗=jmax∣v1−v0∣,没有达到最大加速度 a m a x a_{max} amax;
- T j ∗ = a m a x j m a x T_j^*=\frac{a_{max}}{j_{max}} Tj∗=jmaxamax,达到最大加速度;
请注意,这里讨论的是系统参数对称的。
写成一个式子:
T
j
∗
=
m
i
n
{
∣
v
1
−
v
0
∣
j
m
a
x
,
a
m
a
x
j
m
a
x
}
(3.2)
T_j^*=min\{\sqrt{\frac{|v_1-v_0|}{j_{max}},}\frac{a_{max}}{j_{max}}\}\tag{3.2}
Tj∗=min{jmax∣v1−v0∣,jmaxamax}(3.2)
可规划位移约束条件,不等式成立是因为将加加速度看成无穷大,即一开始就达到最大加速度:
q
1
−
q
0
>
{
T
j
∗
(
v
0
+
v
1
)
1
2
(
v
0
+
v
1
)
[
T
j
∗
+
∣
v
1
−
v
0
∣
a
m
a
x
]
(3.3)
q_1-q_0>\left\{ \begin{aligned} &T_j^*(v_0+v_1) \\\\ & \frac{1}{2}(v_0+v_1)[T_j^*+\frac{|v_1-v_0|}{a_{max}}] \end{aligned}\tag{3.3} \right.
q1−q0>⎩
⎨
⎧Tj∗(v0+v1)21(v0+v1)[Tj∗+amax∣v1−v0∣](3.3)
文中可能会出现以下参数记号:
- T j 1 T_{j1} Tj1:第一组高、低脉冲时间;
- T j 2 T_{j2} Tj2:第二组高、低脉冲时间;
- T a T_a Ta:加速段时间( T a ≥ 2 T j 1 T_a \ge2T_{j1} Ta≥2Tj1);
- T d T_d Td:减速段时间( T d ≥ 2 T j 2 T_d \ge2T_{j2} Td≥2Tj2);
- T v T_v Tv:匀速阶段;
- T T T:规划总时间( T = T a + T d + T v T=T_a+T_d+T_v T=Ta+Td+Tv);
- v l i m = m a x ( q ˙ ( t ) ) v_{lim}=max(\dot q(t)) vlim=max(q˙(t)) 运行的最大速度,如果有匀速段也称为运行速度;
- a l i m = m a x ( q ¨ ( t ) ) a_{lim}=max(\ddot q(t)) alim=max(q¨(t))运行的最大加速度。
规划完成后, v l i m v_{lim} vlim a l i m a_{lim} alim这两个参数在最好情况下等于系统最大速度 v m a x v_{max} vmax和系统最大加速度 a m a x a_{max} amax;他可能根据用户参数进行调整,实际可能小于系统最大速度 v m a x v_{max} vmax和系统最大加速度 a m a x a_{max} amax[3]。
S型规划的最终的目标合理分配A.M.D三个阶段的时间,完成指定用户期望速度。
四、双S曲线时间参数的计算
完成双S型速度规划的关键在于计算时间参数,分别是 T j 1 T_{j1} Tj1, T j 2 T_{j2} Tj2 , T a T_a Ta, T d T_d Td, T v T_v Tv。时间参数计算分为两情况:
- v l i m = v m a x v_{lim}=v_{max} vlim=vmax
- v l i m < v v m a x v_{lim}<v_{vmax} vlim<vvmax
4.1 T v T_v Tv段存在, v l i m = v m a x v_{lim}=v_{max} vlim=vmax
假设 T v T_v Tv段存在,计算 T j 1 T_{j1} Tj1 T j 2 T_{j2} Tj2 。计算这两个参数之前,需要对Jerk作用段( T a T_a Ta T d T_d Td)是否达到最大加速度进行判断:
-
T
a
T_a
Ta段参数计算
( v m a x − v 0 ) j m a x < a m a x 2 (4.1) (v_{max}-v_{0})j_{max}<a^2_{max} \tag{4.1} (vmax−v0)jmax<amax2(4.1)
(4.1)成立,即没有达到规划的最大加速度,没有匀加速段:
T
j
1
=
v
m
a
x
−
v
0
j
m
a
x
,
T
a
=
2
T
j
1
(4.2)
T_{j1}=\sqrt{\frac{v_{max}-v_0}{j_{max}}},T_a=2T_{j1}\tag{4.2}
Tj1=jmaxvmax−v0,Ta=2Tj1(4.2)
(4.1)不成立,则规划可能达到最大加速度:
T
j
1
=
a
m
a
x
j
m
a
x
,
T
a
=
T
j
1
+
v
m
a
x
−
v
0
a
m
a
x
(4.3)
T_{j1}=\frac{a_{max}}{j_{max}},\quad T_a=T_{j1}+\frac{v_{max}-v_0}{a_{max}}\tag{4.3}
Tj1=jmaxamax,Ta=Tj1+amaxvmax−v0(4.3)
-
T
d
T_d
Td段参数计算
( v m a x − v 1 ) j m a x < a m a x 2 (4.4) (v_{max}-v_{1})j_{max}<a^2_{max}\tag{4.4} (vmax−v1)jmax<amax2(4.4)
(4.4)成立,即规划没有达到最大加速度,没有匀加速段:
T j 2 = v m a x − v 1 j m a x , T d = 2 T j 2 (4.5) T_{j2}=\sqrt{\frac{v_{max}-v_1}{j_{max}}},T_d=2T_{j2}\tag{4.5} Tj2=jmaxvmax−v1,Td=2Tj2(4.5)
(4.4)不成立,即规划可能达到最大加速度,:
T j 2 = a m a x j m a x , T d = T j 2 + v m a x − v 1 a m a x (4.6) T_{j2}=\frac{a_{max}}{j_{max}},\quad T_d=T_{j2}+\frac{v_{max}-v_1}{a_{max}}\tag{4.6} Tj2=jmaxamax,Td=Tj2+amaxvmax−v1(4.6)
这样一来,
T
v
T_v
Tv为:
T
v
=
q
1
−
q
0
v
m
a
x
−
T
a
2
(
1
+
v
0
v
m
a
x
)
−
T
d
2
(
1
+
v
1
v
m
a
x
)
(4.7)
T_v=\frac{q_1-q_0}{v_{max}}-\frac{T_a}{2}(1+\frac{v_0}{v_{max}})-\frac{T_d}{2}(1+\frac{v_1}{v_{max}})\tag{4.7}
Tv=vmaxq1−q0−2Ta(1+vmaxv0)−2Td(1+vmaxv1)(4.7)
如果 T v ≥ 0 T_v\ge0 Tv≥0参数计算完成;若 T v < 0 T_v<0 Tv<0则说明假设不成功,需要进一步计算参数。
4.2 T v T_v Tv段不存在, v l i m < v m a x v_{lim}<v_{max} vlim<vmax
这种情况下,
T
v
=
0
T_v=0
Tv=0。假设两个阶段的系统最大加速度
a
m
a
x
a_{max}
amax都存在,那么对应单脉时间分别为:
T
j
1
=
T
j
2
=
T
j
=
a
m
a
x
j
m
a
x
(4.8)
T_{j1}=T_{j2}=T_j=\frac{a_{max}}{j_{max}} \tag{4.8}
Tj1=Tj2=Tj=jmaxamax(4.8)
T a = a m a x 2 j m a x − 2 v 0 + Δ 2 a m a x (4.9) T_a=\frac{\frac{a^2_{max}}{j_{max}}-2v_0+\sqrt{\Delta}}{2a_{max}}\tag{4.9} Ta=2amaxjmaxamax2−2v0+Δ(4.9)
T
d
=
a
m
a
x
2
j
m
a
x
−
2
v
1
+
Δ
2
a
m
a
x
(4.10)
T_d=\frac{\frac{a^2_{max}}{j_{max}}-2v_1+\sqrt{\Delta}}{2a_{max}}\tag{4.10}
Td=2amaxjmaxamax2−2v1+Δ(4.10)
其中
Δ
=
a
m
a
x
4
j
m
a
x
2
+
2
(
v
0
2
+
v
1
2
)
+
a
m
a
x
(
4
(
q
1
−
q
0
)
−
2
a
m
a
x
j
m
a
x
(
v
0
+
v
1
)
)
)
(4.11)
\Delta=\frac{a_{max}^4}{j_{max}^2}+2(v_0^2+v_1^2)+a_{max}\left(4(q_1-q_0)-2\frac{a_{max}}{j_{max}}(v_0+v_1))\right)\tag{4.11}
Δ=jmax2amax4+2(v02+v12)+amax(4(q1−q0)−2jmaxamax(v0+v1)))(4.11)
公式(4.9 ~ 4.11)完成了在最大加速度存在的情况下的轨迹规划[2]。
- 假设成立, T a ≥ 2 T j 1 T_a\ge2T_{j1} Ta≥2Tj1 且 T d ≥ 2 T j 2 T_d\ge2T_{j2} Td≥2Tj2,参数计算完成;
- 假设不成立,
T
a
<
2
T
j
1
T_a<2T_{j1}
Ta<2Tj1或
T
d
<
2
T
j
2
T_d<2T_{j2}
Td<2Tj2,需要进一步计算参数。假设失败意味着至少AP段和DP段至少一个不能到达
a
m
a
x
a_{max}
amax,这种情况非常罕见,这需要对降低规划的加速度要求,一种可行的方法是:按比例衰减加速度
a m a x = γ a m a x 0 < γ < 1 (4.12) a_{max}=\gamma a_{max}\quad0<\gamma<1\tag{4.12} amax=γamax0<γ<1(4.12)
后,根据公式(4.8 ~ 4.11)计算并重新验证条件是否满足,若满足退出,规划完成,反之继续衰减加速度。
在衰减的过程中,可能出现 T a < 0 T_a<0 Ta<0或者 T d < 0 T_d<0 Td<0,这意味着AP和DP段不存在,即对应的 T a = 0 T_a=0 Ta=0 T b = 0 T_b=0 Tb=0。
在迭代过程中若出现,
T
a
<
0
T_a<0
Ta<0,计算方法如下:
T
d
=
2
q
1
−
q
0
v
1
+
v
0
(4.13)
T_d=2\frac{q_1-q_0}{v_1+v_0} \tag{4.13}
Td=2v1+v0q1−q0(4.13)
T j 2 = j m a x ( q 1 − q 0 ) − j m a x ( j m a x ( q 1 − q 0 ) 2 + ( v 1 + v 0 ) 2 ( v 1 − v 0 ) ) j m a x ( v 1 + v 0 ) (4.14) T_{j_2}=\frac{j_{max}(q_1-q_0)-\sqrt{j_{max}(j_{max}(q_1-q_0)^2+(v_1+v_0)^2(v_1-v_0))}}{j_{max}(v_1+v_0)}\tag{4.14} Tj2=jmax(v1+v0)jmax(q1−q0)−jmax(jmax(q1−q0)2+(v1+v0)2(v1−v0))(4.14)
同样的,若
T
d
<
0
T_d<0
Td<0:
T
a
=
2
q
1
−
q
0
v
1
+
v
0
(4.15)
T_a=2\frac{q_1-q_0}{v_1+v_0} \tag{4.15}
Ta=2v1+v0q1−q0(4.15)
T j 1 = j m a x ( q 1 − q 0 ) − j m a x ( j m a x ( q 1 − q 0 ) 2 − ( v 1 + v 0 ) 2 ( v 1 − v 0 ) ) j m a x ( v 1 + v 0 ) (4.16) T_{j_1}=\frac{j_{max}(q_1-q_0)-\sqrt{j_{max}(j_{max}(q_1-q_0)^2-(v_1+v_0)^2(v_1-v_0))}}{j_{max}(v_1+v_0)}\tag{4.16} Tj1=jmax(v1+v0)jmax(q1−q0)−jmax(jmax(q1−q0)2−(v1+v0)2(v1−v0))(4.16)
至此,时间参数计算完成。
4.3 计算实际运行参数 v m a x v_{max} vmax a m a x a_{max} amax
至此五个时间参数 T j 1 T_{j1} Tj1, T j 2 T_{j2} Tj2 , T a T_a Ta, T d T_d Td, T v T_v Tv均已确定,为了保证S型规划始终可用,可能做了如下修改:
- v m a x v_{max} vmax降至 v l i m v_{lim} vlim
- a m a x a_{max} amax降至 a l i m a_{lim} alim
其实规划参数
v
m
a
x
v_{max}
vmax
a
m
a
x
a_{max}
amax理解为期望参数更为合适,降低后的参数
v
l
i
m
v_{lim}
vlim
a
l
i
m
a_{lim}
alim更像是妥协后的实际运行参数。根据时间参数可以计算实际运行参数
v
l
i
m
v_{lim}
vlim
a
l
i
m
a_{lim}
alim:
a
l
i
m
a
=
j
m
a
x
T
j
1
a
l
i
m
d
=
j
m
a
x
T
j
2
(4.17)
a_{lim_a}=j_{max}T_{j1}\quad a_{lim_d}=j_{max}T_{j2}\tag{4.17}
alima=jmaxTj1alimd=jmaxTj2(4.17)
v l i m = v 0 + ( T a − T j 1 ) a l i m a = v 1 − ( T d − T j 2 ) a l i m d (4.18) v_{lim}=v_0+(T_a-T_{j1})a_{lim_a}=v_1-(T_d-T_{j2})a_{lim_d}\tag{4.18} vlim=v0+(Ta−Tj1)alima=v1−(Td−Tj2)alimd(4.18)
五、关于时间参数的分段表达式
时间参数计算完成,关于S型规划就算完成了绝大部分。运用微积分的可求解各部分的分段表达式:
- 加速阶段 AP
a) t ∈ [ 0 , T j 1 ) t\in[0,T_{j1}) t∈[0,Tj1)
{ q ( t ) = q 0 + v 0 t + j m a x t 3 6 q ˙ ( t ) = v 0 + j m a x t 2 2 q ¨ ( t ) = j m a x t q ( 3 ) ( t ) = j m a x (5.1) \left\{ \begin{aligned} &q(t)=q_0+v_0t+j_{max}\frac{t^3}{6} \\ & \dot q(t)=v_0+j_{max}\frac{t^2}{2}\\ &\ddot q(t)=j_{max}t\\ & q^{(3)}(t)=j_{max} \end{aligned} \right. \tag{5.1} ⎩ ⎨ ⎧q(t)=q0+v0t+jmax6t3q˙(t)=v0+jmax2t2q¨(t)=jmaxtq(3)(t)=jmax(5.1)
b) t ∈ [ T j 1 , T a − T j 1 ) t\in[T_{j1},T_a-T_{j1}) t∈[Tj1,Ta−Tj1)
{ q ( t ) = q 0 + v 0 t + a l i m a 6 ( 3 t 2 − 3 T j 1 t + T j 1 2 ) q ˙ ( t ) = v 0 + a l i m a ( t − T j 1 2 ) q ¨ ( t ) = j m a x T j 1 = a l i m a q ( 3 ) ( t ) = 0 (5.2) \left\{ \begin{aligned} &q(t)=q_0+v_0t+\frac{a_{lim_a}}{6}(3t^2-3T_{j1}t+T_{j1}^2) \\ & \dot q(t)=v_0+a_{lim_a}(t-\frac{T_{j1}}{2})\\ &\ddot q(t)=j_{max}T_{j1}=a_{lim_a}\\ &q^{(3)}(t)=0 \end{aligned} \right. \tag{5.2} ⎩ ⎨ ⎧q(t)=q0+v0t+6alima(3t2−3Tj1t+Tj12)q˙(t)=v0+alima(t−2Tj1)q¨(t)=jmaxTj1=alimaq(3)(t)=0(5.2)
c) t ∈ [ T a − T j 1 , T a ) t\in[T_a-T_{j1},T_a) t∈[Ta−Tj1,Ta)
{ q ( t ) = q 0 + ( v l i m + v 0 ) T a 2 − v l i m ( T a − t ) − j m i n ( T a − t ) 3 6 q ˙ ( t ) = v l i m + j m i n ( T a − t ) 2 2 q ¨ ( t ) = − j m i n ( T a − t ) q ( 3 ) ( t ) = j m i n = − j m a x (5.3) \left\{ \begin{aligned} &q(t)=q_0+(v_{lim}+v_0)\frac{T_a}{2}-v_{lim}(T_a-t)-j_{min}\frac{(T_a-t)^3}{6} \\ & \dot q(t)=v_{lim}+j_{min}\frac{(T_a-t)^2}{2}\\ &\ddot q(t)=-j_{min}(T_a-t)\\ &q^{(3)}(t)=j_{min}=-j_{max} \end{aligned} \right. \tag{5.3} ⎩ ⎨ ⎧q(t)=q0+(vlim+v0)2Ta−vlim(Ta−t)−jmin6(Ta−t)3q˙(t)=vlim+jmin2(Ta−t)2q¨(t)=−jmin(Ta−t)q(3)(t)=jmin=−jmax(5.3)
匀速阶段 MP
t ∈ [ T a , T a + T v ) t\in[T_a,T_a+T_v) t∈[Ta,Ta+Tv)
{ q ( t ) = q 0 + ( v l i m + v 0 ) T a 2 + v l i m ( t − T a ) q ˙ ( t ) = v l i m q ¨ ( t ) = 0 q ( 3 ) ( t ) = 0 (5.4) \left\{ \begin{aligned} &q(t)=q_0+(v_{lim}+v_0)\frac{T_a}{2}+v_{lim}(t-T_a) \\ & \dot q(t)=v_{lim}\\ &\ddot q(t)=0\\ &q^{(3)}(t)=0 \end{aligned} \right. \tag{5.4} ⎩ ⎨ ⎧q(t)=q0+(vlim+v0)2Ta+vlim(t−Ta)q˙(t)=vlimq¨(t)=0q(3)(t)=0(5.4)
减速阶段 DP
a) t ∈ [ T − T d , T − T d + T j 2 ) t\in[T-T_d,T-T_d+T_{j2}) t∈[T−Td,T−Td+Tj2)
{ q ( t ) = q 1 − ( v l i m + v 1 ) T d 2 + v l i m ( t − T + T d ) − j m a x ( t − T + T d ) 3 6 q ˙ ( t ) = v l i m − j m a x ( t − T + T d ) 2 2 q ¨ ( t ) = − j m a x ( t − T + T d ) q ( 3 ) ( t ) = j m i n = − j m a x (5.5) \left\{ \begin{aligned} &q(t)=q_1-(v_{lim}+v_1)\frac{T_d}{2}+v_{lim}(t-T+T_d)-j_{max}\frac{(t-T+T_d)^3}{6} \\ & \dot q(t)=v_{lim}-j_{max}\frac{(t-T+T_d)^2}{2}\\ &\ddot q(t)=-j_{max}(t-T+T_d)\\ &q^{(3)}(t)=j_{min}=-j_{max} \end{aligned} \right. \tag{5.5} ⎩ ⎨ ⎧q(t)=q1−(vlim+v1)2Td+vlim(t−T+Td)−jmax6(t−T+Td)3q˙(t)=vlim−jmax2(t−T+Td)2q¨(t)=−jmax(t−T+Td)q(3)(t)=jmin=−jmax(5.5)
b) T ∈ [ T − T d + T j 2 , T − T j 2 ) T\in[T-T_d+T_{j2},T-T_{j2}) T∈[T−Td+Tj2,T−Tj2)
{ q ( t ) = q 1 − ( v l i m + v 1 ) T d 2 + v l i m ( t − T + T d ) + a l i m d 6 ( 3 ( t − T + T d ) 2 − 3 T j 2 ( t − T + T d ) + T j 2 2 ) q ˙ ( t ) = v l i m + a l i m d ( t − T + T d − T j 2 2 ) q ¨ ( t ) = − j m a x ( t − T + T d ) q ( 3 ) ( t ) = 0 (5.6) \left\{ \begin{aligned} &q(t)=q_1-(v_{lim}+v_1)\frac{T_d}{2}+v_{lim}(t-T+T_d)+ \frac{a_{lim_d}}{6}\left(3(t-T+T_d)^2-3T_{j2}(t-T+T_d)+T_{j2}^2\right)\\ & \dot q(t)=v_{lim}+a_{lim_d}(t-T+T_d-\frac{T_{j2}}{2})\\ &\ddot q(t)=-j_{max}(t-T+T_d)\\ &q^{(3)}(t)=0 \end{aligned} \right. \tag{5.6} ⎩ ⎨ ⎧q(t)=q1−(vlim+v1)2Td+vlim(t−T+Td)+6alimd(3(t−T+Td)2−3Tj2(t−T+Td)+Tj22)q˙(t)=vlim+alimd(t−T+Td−2Tj2)q¨(t)=−jmax(t−T+Td)q(3)(t)=0(5.6)
c) t ∈ [ T − T j 2 , T ] t\in[T-T_{j2},T] t∈[T−Tj2,T]
{ q ( t ) = q 1 − v 1 ( T − t ) − j m a x ( T − t ) 3 6 q ˙ ( t ) = v 1 + j m a x ( T − t ) 2 2 q ¨ ( t ) = − j m a x ( T − t ) q ( 3 ) ( t ) = j m a x (5.7) \left\{ \begin{aligned} &q(t)=q_1-v_1(T-t)-j_{max}\frac{(T-t)^3}{6} \\ & \dot q(t)=v_1+j_{max}\frac{(T-t)^2}{2}\\ &\ddot q(t)=-j_{max}(T-t)\\ &q^{(3)}(t)=j_{max} \end{aligned} \right. \tag{5.7} ⎩ ⎨ ⎧q(t)=q1−v1(T−t)−jmax6(T−t)3q˙(t)=v1+jmax2(T−t)2q¨(t)=−jmax(T−t)q(3)(t)=jmax(5.7)
六、考虑 q 1 < q 0 q_1<q_0 q1<q0
为了统一两种情况,需要进行以下处理:
首先,转换初始值参数:
q
0
=
σ
q
^
0
q
1
=
σ
q
^
1
v
0
=
σ
v
^
0
v
1
=
σ
v
^
1
(6.1)
q_0=\sigma \hat q_0\quad q_1=\sigma \hat q_1 \quad v_0=\sigma \hat v_0\quad v_1=\sigma \hat v_1\tag{6.1}
q0=σq^0q1=σq^1v0=σv^0v1=σv^1(6.1)
其中,
σ
=
s
i
g
n
(
q
^
1
−
q
^
0
)
(6.2)
\sigma=sign(\hat q_1- \hat q_0)\tag{6.2}
σ=sign(q^1−q^0)(6.2)
其次,转换规划参数:
{
v
m
a
x
=
(
σ
+
1
)
2
v
^
m
a
x
+
(
σ
−
1
)
2
v
^
m
i
n
v
m
i
n
=
(
σ
+
1
)
2
v
^
m
i
n
+
(
σ
−
1
)
2
v
^
m
a
x
a
m
a
x
=
(
σ
+
1
)
2
a
^
m
a
x
+
(
σ
−
1
)
2
a
^
m
i
n
a
m
i
n
=
(
σ
+
1
)
2
a
^
m
i
n
+
(
σ
−
1
)
2
a
^
m
a
x
j
m
a
x
=
(
σ
+
1
)
2
j
^
m
a
x
+
(
σ
−
1
)
2
j
^
m
i
n
j
m
i
n
=
(
σ
+
1
)
2
v
^
m
i
n
+
(
σ
−
1
)
2
v
^
m
a
x
(6.3)
\left\{ \begin{aligned} &v_{max}=\frac{(\sigma+1)}{2}\hat v_{max}+\frac{(\sigma-1)}{2} \hat v_{min} \\ &v_{min}=\frac{(\sigma+1)}{2}\hat v_{min}+\frac{(\sigma-1)}{2} \hat v_{max}\\ &a_{max}=\frac{(\sigma+1)}{2}\hat a_{max}+\frac{(\sigma-1)}{2} \hat a_{min}\\ &a_{min}=\frac{(\sigma+1)}{2}\hat a_{min}+\frac{(\sigma-1)}{2} \hat a_{max}\\ &j_{max}=\frac{(\sigma+1)}{2}\hat j_{max}+\frac{(\sigma-1)}{2} \hat j_{min}\\ &j_{min}=\frac{(\sigma+1)}{2}\hat v_{min}+\frac{(\sigma-1)}{2} \hat v_{max} \end{aligned} \right. \tag{6.3}
⎩
⎨
⎧vmax=2(σ+1)v^max+2(σ−1)v^minvmin=2(σ+1)v^min+2(σ−1)v^maxamax=2(σ+1)a^max+2(σ−1)a^minamin=2(σ+1)a^min+2(σ−1)a^maxjmax=2(σ+1)j^max+2(σ−1)j^minjmin=2(σ+1)v^min+2(σ−1)v^max(6.3)
最后,输出转换:
{
q
^
(
t
)
=
σ
q
(
t
)
q
^
˙
(
t
)
=
σ
q
˙
(
t
)
q
^
¨
(
t
)
=
σ
q
¨
(
t
)
q
^
(
3
)
=
σ
q
(
3
)
(
t
)
(6.4)
\left\{ \begin{aligned} &\hat q(t)=\sigma q(t)\\ &{\dot{ \hat q}(t)}=\sigma \dot q(t)\\ &{\ddot{ \hat q}(t)}=\sigma \ddot q(t)\\ &\hat q^{(3)}=\sigma q^{(3)}(t) \end{aligned} \right. \tag{6.4}
⎩
⎨
⎧q^(t)=σq(t)q^˙(t)=σq˙(t)q^¨(t)=σq¨(t)q^(3)=σq(3)(t)(6.4)
参考文章
[1] 《多轴插补为什么普遍使用梯形速度曲线?》https://www.zhihu.com/question/47474538/answer/106250869
[2] 田军锋, 林浒, 姚壮, et al. 数控系统S型曲线加减速快速规划研究[J]. 小型微型计算机系统, 2013(01):168-172.
[3] Biagiotti, Luigi, Melchiorri, Claudio. Trajectory Planning for Automatic Machines and Robots[J]. 2009.
推导提示1:假如系统可以提供无穷大的 j m a x j_{max} jmax ,运动的规划将会变成加速度始终为 a m a x a_{max} amax 的匀加速运动,对应的时间 t i d e a l = ( v m a x − v 0 ) / a m a x t_{ideal}=(v_{max}-v_0)/a_{max} tideal=(vmax−v0)/amax,实际上,假设所有的时间都用来进行加加速,对应的时间为 t = a m a x / j m a x t=a_{max}/j_{max} t=amax/jmax,因为 t i d e a l < t t_{ideal}<t tideal<t,所以有: ( v m a x − v 0 ) j m a x < a m a x 2 (v_{max}-v_0)j_{max}<a_{max}^2 (vmax−v0)jmax<amax2
推导提示2: 一个物体的初速度为 v 0 , a 0 = 0 v_0,a_0=0 v0,a0=0,以恒定加加速度 j j j 加速至 v 1 , a m a x v_1,a_{max} v1,amax ,理论上最短时间为 ∣ v 1 − v 0 ∣ j m a x \sqrt{\frac{|v_1-v_0|}{j_{max}}} jmax∣v1−v0∣ 。推导提示: a m a x = 2 ⋅ j m a x Δ v a_{max}=2\cdot j_{max}\Delta v amax=2⋅jmaxΔv, Δ v = 1 2 a m a x ⋅ t \Delta v=\frac{1}{2}a_{max}\cdot t Δv=21amax⋅t。