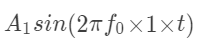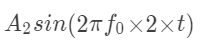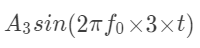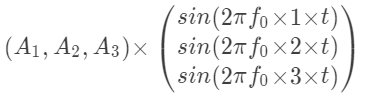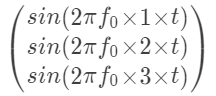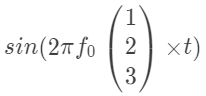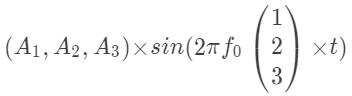微信公众号: MitchHong微信号: ASparkleSubscription作者: Mitch Hong
Untitled
刚刚中午在写作业的时候突然想起来的这个方法,感觉应该有点用,就趁热做了这篇推送来分享一下,哈哈哈。

呐,就是上图中红框的那道题,要把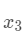
(本人数学菜鸟)。哈哈,不过幸好还记得点线性代数上的一些知识,试了一下算出来了。下面先放上代码再简单解释一下。
A1 = 1;
A2 = 0.5;
A3 = 0.2;
A = [A1, A2, A3];
f0 = 5; %Hz
i = [1:3]';
x3 = @(t) A * sin(2*pi*f0* i * t);
fs = 2048; % 采样频率Hz,每秒2048个点
Ts = 1 / fs; % 采样间隔
n = 0 : 2048 - 1; % 2k个点(正好采1s)
t = n .* Ts; % 时间t
plot(t, x3(t))
下面这是结果
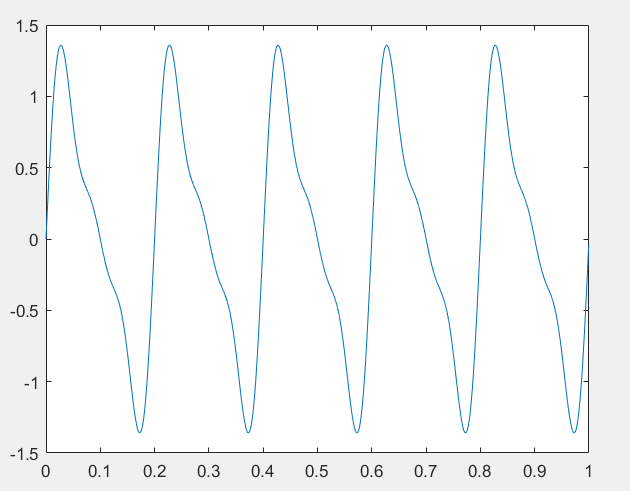
现在看一下题中的那个式子,它就是下面这三行相加:这就能写成到这还没结束上面这个矩阵可以写成如下的形式嘿嘿,所以那个题中的那个和式可以写成如下的形式这便是程序中的这行了
x3 = @(t) A * sin(2*pi*f0* i * t);
注意,A是行向量,i是列向量。到此这个小技巧便说完了,实际上还是数学知识,不算是什么小技巧。艾,这个MarkDown中用latex插入公式简直太好用了,夸一下。
But,要是这个线代中矩阵的乘法都一点也不记得的话,对上面的这个方法没信心,那还是用循环把,如下:
x = 0;
for i = 1 : length(A)
x = x + A(i).*sin(2*pi*f0*i .*t);
end
sum(x == x3(t)) % 和上面利用矩阵运算的出来的结果对比一下,看看两个算出来的值是否都一样
这个在命令行中输出的结果如下
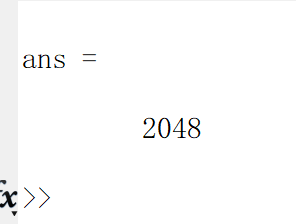
哈哈,说明这2048个点都一样,说明上面用矩阵运算算出来的结果是对的,自信点,哈哈。
本篇内容不多,写了一个多小时,阅读可能就几分钟就读完了。。。
还有昨天那篇推送中的远程仓库链接,忘改成公有的了,这里重新放一下:https://gitee.com/mitchhong/ArrayADT.git