代码：github
原文：原文

摘要

尽管多无人机系统（UAVs）在快速自主探索方面具有巨大潜力，但仍未受到足够的关注。在本文中，我们提出了一种基于去中心化无人机队伍的快速协同探索（RACER）方法。为了有效地调度无人机，采用基于在线网格空间分解的配对交互方法，确保所有无人机同时探索不同的区域，仅使用异步和有限的通信。此外，我们优化了未知空间的覆盖路径，并通过车辆路径规划问题将工作负载均衡分配给每个无人机。在任务分配的基础上，每个无人机不断更新覆盖路径并逐步提取关键信息来支持探索规划。分层规划器寻找探索路径，细化局部视点，并生成最短时间的轨迹以顺利安全地探索已知空间。所提出的方法被广泛评估，展现了高效的探索能力、可扩展性和在有限通信下的鲁棒性。此外，首次实现了在真实世界中完全去中心化的多无人机协同探索。我们将发布我们在现实世界中的开源实现。
关键词
空中系统、航空系统、应用、协作机器人、感知与自主

I. 引言

自主探索利用自主车辆绘制未知环境，是多个机器人应用（如检查、搜救等）中的基础问题。最近，大量文献研究了无人机（UAVs），尤其是四旋翼无人机的自主探索。研究表明，无人机尤其适合高效探索复杂环境，得益于其灵活性和敏捷性。

尽管取得了显著进展，但大多数研究仅关注单一无人机的探索，而对多无人机系统的关注较少。然而，使用一支无人机队伍拥有巨大的潜力，因为它不仅能加快探索的完成，还比单一无人机更能容忍故障。在本文中，我们通过引入基于去中心化无人机队伍的快速协同探索（RACER）方法来填补这一空白。

迄今为止，开发一种稳健、灵活且高效的多无人机探索系统一直充满挑战。首先，协调多机器人系统的方法通常依赖于一个中央控制器或需要可靠的通信，这在实际应用中经常面临不可靠和范围有限的通信问题，使得协调变得脆弱且效果差。为提高系统的灵活性和稳健性，需要一种去中心化协调方法，能够在通信需求较少的情况下工作。其次，许多多机器人探索方法仅考虑前沿或视点的分配问题。由于未考虑每个无人机实际探索的区域，策略往往会导致机器人之间的干扰和工作负载分配不均。并且，全球的覆盖路径没有被考虑，因此无人机可能会重复访问相同的区域，显著降低整体效率。为了充分发挥系统的潜力，需要更精细的协同策略。最后，每个无人机应能够充分利用其能力来完成任务。为此，每个无人机需要能够快速响应环境变化，规划出合适的运动轨迹，使其能够有效导航并高效避开之前未发现的障碍物以及其他系统成员。

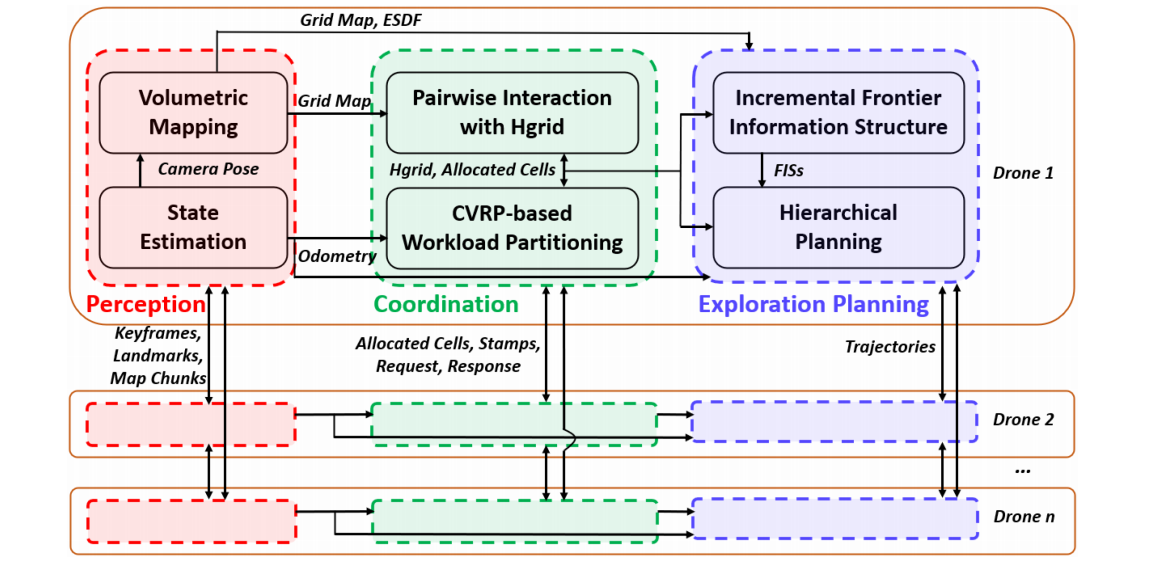
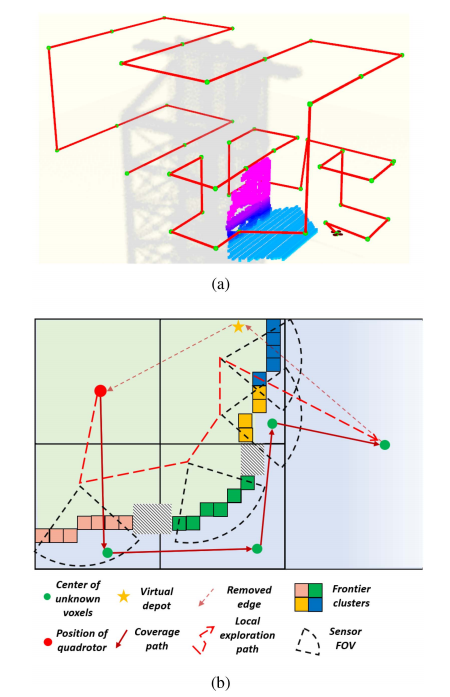
图1. 我们的多旋翼自主探索系统概述，包括感知、协调和探索规划模块。

在本文中，我们提出了一种系统的去中心化协调和规划方法，以实现快速协同探索，该方法考虑了上述提到的困难，如图1所示。为了有效地协调四旋翼无人机，整个未知空间不断在线细分为网格，并通过配对交互将其分配给各个四旋翼。该方法仅需要异步和不可靠的通信，仅通过相邻四旋翼之间的通信即可，确保四旋翼同时探索不同的区域而不相互干扰。此外，还提出了一种容量约束的车辆路径规划（CVRP）问题公式，以实现更高效的协作。它最小化了多个全局覆盖路径（CP）的长度，并平衡了分配给每个四旋翼的工作负载，有效防止了重复探索和不公平的工作负载分配。在任务分配的基础上，每个四旋翼不断更新其CP，提供有效的全局路径来探索未知空间。在CP的指导下，分层规划器找到局部路径，细化视点，并生成最短时间轨迹，依次进行快速探索。整个系统计算开销低且具备可扩展性，能够使团队快速响应环境变化，从而持续进行快速探索。本文的贡献总结如下：

1. 基于在线网格分解的配对交互方法，将未知空间的位置细分，确保四旋翼无人机只通过异步和有限的通信共同探索不同的区域。
2. 一种最小化全局覆盖路径（CP）长度并平衡分配给每个四旋翼的工作负载的CVRP公式。它进一步增强了四旋翼队伍之间的协作。
3. 从[1]扩展的分层探索规划器，结合全局覆盖路径的引导，从而提高探索效率。规划器中还集成了互相避碰机制。
4. 我们将所提出的方法与多机器人状态估计结合，实现了完全自主探索，并在具有挑战性的现实环境中进行实验。我们将发布我们的系统源代码。

II. 相关工作

A. 自主探索

机器人探索，旨在绘制未知环境，是近年来随着移动机器人技术发展而研究的一个重要问题。一些研究集中在快速覆盖[2][3]，而其他研究则更加注重精确重建[4][5]。一种经典的探索方法是基于前沿的策略，这种方法最早在[6]中提出，并在[7]中进行了更为全面的评估。沈等[8]采用了一种基于随机微分方程的策略，旨在寻找三维环境中的前沿区域。与原始方法[6]选择最近的前沿作为目标不同，Cieslewski等[2]选择最小化视野范围（FOV）内速度变化的前沿。这种策略有助于维持高速飞行，并比[6]中的方法展现出更高的效率。邓等[9]提出了一种可微分的公式，适用于基于梯度的路径优化。基于前沿的方法具有简便性的优势，因为它们通常仅考虑与运动相关的目标来生成路径。其他方法还引入了信息增益来评估候选动作的有效性[10][11]。

另一类方法是基于采样的策略，这些方法随机选择候选视点，并评估它们的信息增益，以探索未知空间。由于这些方法通常量化信息增益以生成更多的候选视点，因此计算负担较大。基于采样的方法与下一个最佳视点（NBV）[12]紧密相关，其中视点被用来完整地建模一个场景。Bircher等人[13]首次提出了三维探索中的NBV概念。它快速扩展随机树（RRTs），在无障碍空间中执行，并以递归的方式生成最有信息量的边。后来，定位的不确定性[14]、视觉重要性[15]和检查[16]等问题也在[13]的框架下进行了考虑。为了重用先前的信息，Dharmadhikari等[3]提出了动态采样可行的运动原语，以实现更高的飞行速度。在[19]中，一种二维流形根据地图进行动态适应，从而指导视点的采样，加速了采样计算，但在复杂结构的情况下可能会出现次优解。

结合前沿方法和基于采样的方法也有一些研究[1][5][20][21][22][23][24]。Charrow等[20]和Selin等[21]提出了基于前沿生成全局路径以及采样路径以探索局部区域的方案。Meng等人[22]讨论了一种从前沿区域采样视点并生成通过该区域的全局路径的方法。Song等[5]使用基于采样的路径生成探索路径，并且针对机器人未完成的表面进行视点采样，从而计算出最短的访问路径，该路径与粗略的全局路径相连接。与基于采样的方法相比，这些方法的计算量较小，因为它们仅需在前沿区域采样视点。我们的前期工作[1]提出了一种更加计算高效的方法，该方法从前沿区域采样视点并避免了计算开销。

给定候选目标（如前沿区域或采样视点），大多数现有方法采用贪婪策略来做出决策。例如，选择最接近的前沿[6]或最大化即时信息增益[3][4][13][17]。然而，贪婪策略忽略了有效的全局路径，导致不必要的重复访问，降低了整体效率。这个问题在[22]中部分得到了解决，在我们之前的工作[1]中，我们通过将旅行商问题（TSP）形式化来计算访问候选视点的最短路径。然而，他们仅考虑了从采样视点生成的全局路径，且仍然缺乏高效探索整个未知区域的能力。在本工作中，我们扩展了[1]的工作，结合了一个高效的覆盖路径（CP），引导每个四旋翼按合理的顺序探索不同的未知区域。

B. 多机器人协作

与单一机器人系统相比，多机器人系统显然具有更大的优势，如更快地覆盖环境和提高对单点故障的鲁棒性。多机器人探索的关键是适当分配任务，以避免任务冲突并使得每个机器人能同时探索不同的区域。一个常见的策略是与所有机器人进行通信，并通过集中式服务器分配任务[25][26][27][28][29]。在这些方法中，最简单的方案是迭代分配[25][26]，通过该算法，机器人和目标之间的配对由贪婪算法选择，基于距离和信息增益。然而，这种策略仅为每个机器人分配一个目标，当多个机器人被分配到相邻目标时，这种方法可能效果不佳。为克服这一限制，一些方法基于区域划分[27][30]和多重旅行商问题（mTSP）[28][29][31]提出。Wurm等人[27]通过Voronoi图将已探索区域分为不同的区域段。通过将机器人分配到不同的区域段而非单一目标，机器人得以更均匀地分布到整个环境中。类似地，广度优先搜索（BFS）式的聚类算法将分解区域进行分配。Faigl等[28]和Dong等[29]通过将协调问题形式化为mTSP来实现这一目标。由于该问题是NP-hard问题，提出了分治方案来计算近似解。Faigl等人[28]将所有目标分配给簇，通过变种的K-means算法将簇分配给机器人。Dong等[29]提出了一个离散的最优运输问题模型来进行目标分配，目标是为每个机器人分配所有目标的最佳路径，该路径由TSP确定。Hardouni等[31]采用TSP贪婪算法来贪婪地为每个机器人分配视点集群。然而，他们也考虑了去中心化架构，其中假定通信是完美的。
一个集中式协调的主要问题是要求所有机器人保持与服务器的通信。然而，这一要求在实际中通常不可行，例如，在探索大规模环境时，机器人可能会远离服务器，或者信号在拥挤环境中可能频繁丢失。此外，服务器失败时，机器人无法继续进行探索。相比之下，去中心化协调[32][33][34][35][36][37][38]对通信丢失和故障更加稳健，因为系统中的每个智能体都能独立操作。第一个去中心化的多机器人探索方法在[32]中被提出，其中所有机器人共享地图信息并移动到最近的前沿区域。尽管这种方法简单且完全去中心化，但协调效果不理想，因为可能有多个机器人移动到同一个地方。为解决这一问题，提出了一种基于蚁群算法的策略[39]，机器人可以标记已探索的区域，以防止队友再次访问同一位置。然而，将该方法应用于现实世界仍然存在挑战。另一种去中心化协调方法利用基于拍卖的机制[33][34][35]。Zlot等人[33]和Smith等人[34]通过使用分布式单一标价拍卖解决了机器人之间的冲突。为了共同考虑多个目标的分配，Berhault等人[35]提出了组合拍卖方法。除了基于拍卖的方法外，Corah等人[36]扩展了贪婪分配方法，转向了分布式方法；然而，该过程通常需要多次通信以协调机器人。Corah等人[40]还讨论了不同的目标函数和目标状态，它们要求机器人以更高频率的通信进行协作。

对于上述去中心化方法，机器人之间的通信通常是情景性和偶然性的，因为连接不是事先规划好的。在某些任务中，需要定期的机器人与基站会合，这在某些时刻强制更新信息。为此，其他方法将机器人分配到不同角色，其中某些机器人探索新区域，其他机器人则负责传递信息[43][44][45]。这两类机器人通过适当选择会合点进行协调，在这些会合点，它们假设在特定的通信模型下进行连接[46]。与这些方法不同，Gao等人[47]提出了一种模型，考虑到机器人之间的周期性会面。另一类更为严格的工作强制执行机器人之间的连续通信[48]，这要求机器人之间有视距通信。Rathman等人[49]讨论了一种基于搜索的分布式方法，该方法不允许持续连接。Jensen等人[51][52]提出了系统，允许机器人重新连接，支持在探索过程中保持高频率的通信。然而，作为副作用，探索过程可能会受到相当大的限制。

在本文中，我们考虑了一个机器人团队探索未知场景的任务，目标是尽可能快速地完成探索，同时需要与基站实时传输数据。我们的协调方法灵感来源于[38]。然而，我们的方法不同于该方法，采用网格作为基础任务单元，以实现更有效的任务分配。与此同时，我们不再近似每对机器人的旅行距离，而是使用局部下坡算法来改善任务分配的局部优化[38]，通过最小化精确的旅行距离来寻找两个机器人之间的最优任务分配。我们还设计了一种请求-响应方案，用于解决不公平的交互机会和冲突交互的问题。

C. 多机器人探索系统

多个研究工作研究了自主探索的多机器人系统，重点关注系统的不同方面。在DARPA地下挑战赛中，机器人团队用于地下环境的探索，激发了这些研究[53][54][55][56][57][58]。这些机器人通常配备了多种传感器和高增益的通信天线，以及定位、地图构建和路径规划等能力，能够在复杂的大规模地下环境中搜索目标物体。这些工作专注于集成硬件和算法组件，以及地下工程适应性以增强系统的鲁棒性。然而，这些系统通常更多依赖于中心化控制来完成任务。与此同时，机器人间的协调较少受到关注，通常采用简单的策略，如贪婪分配[53]或拍卖[55][57]。Petráček等[58]也讨论了一种归巢策略，通过该策略，机器人团队能够与基站建立通信连接。除此之外，一些研究者还研究了系统的映射[59][60]和协作通信[61]。Corah等[59]采用了高斯混合模型进行全局地图构建，从而保持较小的内存占用，并降低通信量。Tian等[60]提出了一种基于周期一致性的数据关联方法，改善了协作定位和地图构建的精度。Cesare等人[61]提出了一种协作方案，允许电量较低的机器人充当中继，以改善团队成员间的通信。在[62]中，提出了一种用于轻型飞行机器人的梯度算法，支持机器人间的随行导航和接收信号强度来避免碰撞。这允许机器人在较低效率和无法在线准确导航的情况下探索未知环境。在这些研究工作中，有些研究了去中心化的算法，以确保即使在间歇性通信的情况下，机器人也能有效地协作。此外，部分工作还提出了通过最小化覆盖路径（CP）长度来平衡工作负载，充分发挥系统的整体能力。

D. 四旋翼运动规划

与探索相关的是局部轨迹重新规划，其中基于梯度的方法获得了广泛的应用[63][64][65][66][67][68][69]。这些方法由Ratliff等人[70]进行综述，并扩展到多项式轨迹[63][64]和B样条轨迹[65]。最近，Zhou等人[66][67][68]进一步利用B样条的性质，使用拓扑引导路径和主动感知来实现复杂场景中的激进飞行。通过消除距离计算，轨迹优化的计算时间得到了进一步减少[69]。

为了避免机器人之间的碰撞，研究了去中心化方法[71][72][73][74][75][76]。速度障碍方法用于避免具有不同约束的机器人发生碰撞[71][72][73]。Liu等人[74]提出了一种异步方法来避免障碍物和其他车辆。Park等人[75]采用了飞机航道和Bernstein多项式来生成可行的轨迹。Zhou等人[76]将梯度重新规划方法[69]扩展到多机器人系统，用于避免四旋翼之间的相互碰撞。

我们的轨迹规划方法基于[1]和[66]中的方法，生成安全且最短时间的轨迹以进行快速探索。我们通过使用四旋翼之间的异步通信，避免了四旋翼之间的相互碰撞。

III. 系统概述

总体的多四旋翼探索系统如图1所示。与最近的研究工作[2][4][13]相似，我们的目标是构建一个指定空间的完整体积地图。系统中的每个四旋翼都执行去中心化的状态估计以定位自身和其他四旋翼。在实验中，我们将状态估计方法[77]集成到系统中。给定估计的相对姿态，每个四旋翼在通信可用时频繁地交换地图信息，以便作出更为明智的决策。状态估计和地图构建的实施细节见第七节。

四旋翼团队的协调依赖于在线网格分解和配对交互。每个四旋翼在探索并收集信息时，整个未知空间被不断地按预定义的边界划分为多个网格，并不断细分成包含不同大小的网格单元，这些网格单元作为分配任务的基本单元。四旋翼按照请求-响应方案进行调度，配对的四旋翼通过配对交互交换信息，并更新网格单元的所有权。这些网格单元通过CVRP公式进行划分，最小化了所有四旋翼之间的覆盖路径长度，从而平衡了分配给每个四旋翼的工作负载。分配的目标是探索整个未知空间，如第V-A节所述。

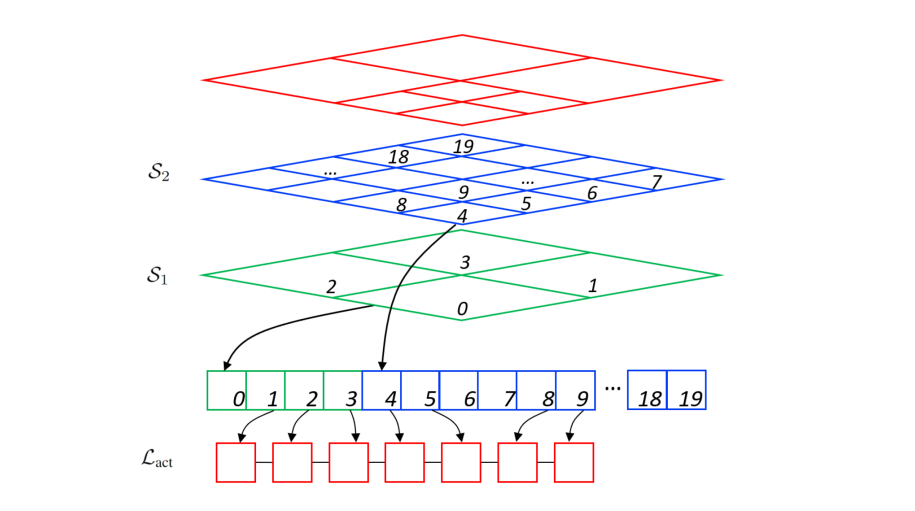
图2. 具有两级的2D网格分解示例及其通过单一数组的实现。为了方便起见，我们在此展示2D网格，但在实现中使用的是3D网格。当前环境的分解（红色部分）由列表$L_{\text{act}}$记录。

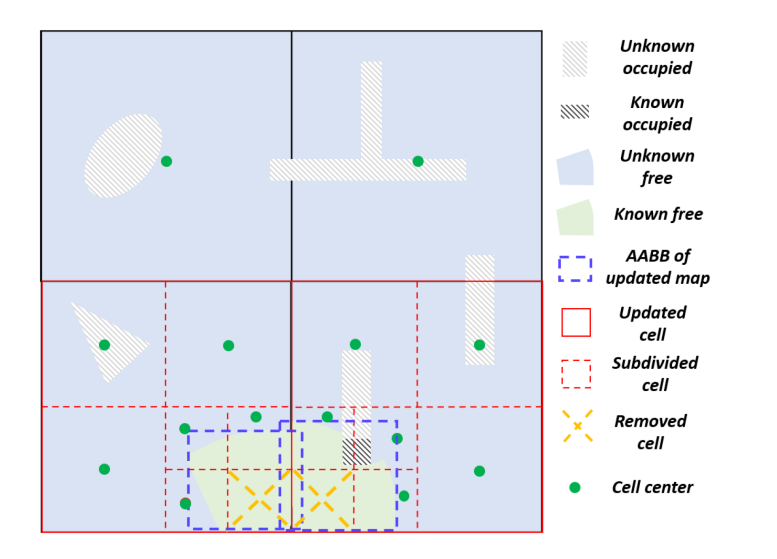
图3. 更新三层网格的过程示意图。与任何$B_m$中的AABB重叠的网格单元将被更新，并在必要时细分为更小的单元。已完全覆盖的单元将从$L_{\text{act}}$中移除。

IV. 基于网格的配对交互

我们利用配对交互来分配任务，只需要与附近的四旋翼进行间歇性通信。与大多数分配前沿区域和视点的方法不同，我们的任务表示基于在线网格（hgrid）分解未知空间，这确保了不同区域的联合探索，同时避免了四旋翼之间的干扰。

A. 网格分解

我们不断地将整个未知空间在线分解为不相交的区域，代表着分配给四旋翼的基本任务单元。此处考虑的分解方法是网格（hgrid），它是一种分层的分解方法，包含从粗到细的不同分辨率的网格单元。每个网格单元的大小可以适应多机器人协作。对于网格，每个层级$l$中的每个单元被均匀地细分为八个子单元（在二维情况下为四个子单元），即$l+1$层中的每个单元。网格的不同层次提供了足够的灵活性来表示未知区域。网格的示例如图2和图3所示。

给定在线构建的地图，每个四旋翼维护一个位于相同世界坐标系中的网格分解。统一坐标系的建立在第七节中详细介绍。网格包含多个层次{S1, S2, …, SL}，其中S1是最粗的网格单元，SL是最细的网格单元。对于每个网格单元，它记录了包含的未知体素数量以及这些未知体素的质心位置。为了存储整个网格，我们使用单一数组，并采用类似于标准三维网格的映射方式。我们将空间离散化为$h_l=h_{l,x}\times h_{l,y}\times h_{l,z}$，并在$S_l$中存储每个单元。对于每个整数值的网格坐标为$(i_l,j_l,k_l)$，其索引由以下公式确定：

$$\gamma (i_l,j_l,k_l)=i_l{h}_{l}x+j_l{h}_{l}z+k_l+\sum _{m=1}^l{h}_{m-1},h_0=0.\text{\hspace{1em}(1)}$$

几何上，网格（hgrid）类似于基于八叉树的分解[79][80]，但它是通过使用数组实现的，从而允许$O(1)$的任何单元的检索。此外，我们在实现中采用的线性化数据结构增加了数据局部性，从而提高了CPU数据缓存命中率，进而提升了整体性能[78]。

B. 在线网格更新

为了表示将被四旋翼覆盖的未知区域的分解，使用了一个列表$L_{\text{act}}$，如图2所示。在探索过程中，它存储了所有未完全探索的网格单元的子集，这些单元尚未细分为更精细的单元，并且可以通过传感器访问。与此同时，为了便于网格的更新，我们记录了 B m = { B 1 , B 2 , … , B M } B_m = \{B_1, B_2, \dots, B_M\} Bm​={B1​,B2​,…,BM​}，这些是更新的地图区域的轴对齐边界框（AABBs），包括四旋翼本身探索的区域以及邻近四旋翼共享的区域。

在线网格分解的未知空间如图3和算法1所示。最初，环境是完全未知的，并且分解为最粗的网格单元，即$L_{\text{act}}$仅包含S1中的单元。随着四旋翼构建并共享地图，某些区域逐步细分为更精细的单元，以表示尚未探索的未知区域。网格的更新过程通过反复迭代每个单元$k$在$L_{\text{act}}$中的遍历来进行，并筛选出与任何$B_m\in B_m$有重叠的单元（第2行）。这些单元的质心和未知体素数目将重新计算（第4行）。然后，如果某个体素$k$的包含体素的某一比例${\alpha }_k$已经被探索，并且$k$不在最细层次时，它将被细分为子单元（第5–9行）。相应地，这意味着从$L_{\text{act}}$中移除$k$并将其细分的单元添加到下一级（第10行）。与此同时，如果$k$是最细层次并且只包含少量未知体素时，它将从$L_{\text{act}}$中移除（第11-12行）。最后，质心不可达的单元将从$L_{\text{act}}$中移除（第13-14行），从而去除那些传感器无法覆盖的区域，比如厚墙内的空间。

C. 基于网格的配对交互

配对交互的灵感来源于[38]，其中任务分配问题被分解为可以通过四旋翼对来解决的子问题。当两个机器人进行交互时，基于它们之前的前沿之间的相对位置，执行局部任务。这样，任务被分配到分布式系统中，通信需求显著减少，因为此时仅需两个四旋翼之间进行通信。

我们的配对交互方法进一步改进了[38]，考虑了所有交互四旋翼之间的网格单元$q_i$，并且更加注重任务分配的优化。通过这种方式，任务分配的效率和精确度得到了提高。
任务分配问题通过最小化精确的路径长度来找到最优分配，而不是通过贪婪地减少近似路径长度来实现。具体来说，设$T_i$和$T_j$是配对交互前的两个子集，目标是找到两个新的子集$T_i^{\prime }$和$T_j^{\prime }$，使得$T_i\cup T_j=T_i^{\prime }\cup T_j^{\prime }$且$T_i^{\prime },T_j^{\prime }$最小化覆盖路径（CP）的总体长度。在没有中央计算机调度的情况下，四旋翼可能会以不均匀的方式互相交互，这不利于任务的有效分配。此外，一个四旋翼可能会与多个其他四旋翼同时交互，产生多个冲突的分配结果。为了解决这两个问题，提出了一种请求响应方案，如算法2所示。作为初步步骤，几种类型的信息会定期广播，以确保附近的四旋翼保持共同的知识。以四旋翼$q_i$为例，它广播属于网格单元的信息，并将最后一次尝试配对交互的时间戳标记为$T_i$和$q_i.Tatt$，分别表示四旋翼的目标任务和交互尝试时间。此外，$q_i$记录与其他四旋翼的最新成功交互的时间戳 { T suc , j ∣ j ∈ [ 1 , N q ] ∖ i } \{T_{\text{suc},j} | j \in [1, N_q] \setminus i\} {Tsuc,j​∣j∈[1,Nq​]∖i}。

交互过程从寻找与$q_i$有通信的附近四旋翼开始（第4-5行）。那些在短时间$e_{att}$内已尝试过其他交互的四旋翼将不再考虑（第6-7行），以避免四旋翼同时与多个其他四旋翼交互，通常会导致冲突的交互结果。在这些四旋翼中，我们选择$q_n$，它是与$q_i$成功交互的时间最长的四旋翼（第8-9行），以确保其他四旋翼也有相似的机会与$q_i$交互。然后，找到适当的任务分配，并向$q_n$发送包含结果的请求消息（第10-11行）。具体的分配方法在第V-A节中进行了详细介绍。最后，它更新$T_i$和$q_n$并等待$e_{att}$时间内的响应（第12-13行）。只有在接收到成功响应（succ）时，任务分配结果才会更新，并由$q_i$和$q_n$共同更新（第14-24行）；否则，该交互将被忽略，新任务分配将稍后再试（第19行）。有时$q_n$可能只请求与另一个四旋翼$q_j$的交互。
并广播更新的时间戳。由于通信延迟，当$q_i$尝试与$q_n$交互时，该时间戳可能无法获取。在这种情况下，双重检查确保$q_n$不会与$q_i$和$q_j$同时交互，从而避免了冲突的任务分配。理论上，与集中式方法相比，配对交互可能会找到次优的任务分配。然而，经过一次机器人之间的交互，它迅速达到了一个有前景的分配，正如我们在第VIII-D节的定量研究中所示。此外，值得注意的是，配对交互并不一定减少通信事件。相反，它简化了通信结构，只要求两个机器人同时进行协商，这使得它对不稳定的通信更加有韧性。

V. 基于CVRP的工作负载划分

为了适当地划分属于一对交互四旋翼的网格单元（见算法2），我们提出了一种基于CVRP的公式。其核心思想是最小化四旋翼覆盖路径（CP）的总体长度，并平衡分配给它们的未知空间的量，从而使它们更加有效地协作。

A. CVRP公式

网格单元的最优CP可以通过车辆路径规划问题（VRP）[81]来求解，VRP是TSP的推广，适用于多辆车的情况。在我们的设置中，有两辆车对应于一对交互四旋翼$q_1$和$q_2$。

成本矩阵：假设有$N_h$个网格单元，非对称VRP涉及$N_h+3$个节点，其中$N_h$个节点对应网格单元，两个节点分别对应于四旋翼$q_1$和$q_2$，一个节点对应虚拟仓库。相关的成本矩阵$C_{\text{avrp}}\in {\mathbb{R}}^{(N_h+3)\times (N_h+3)}$如下所示：

$$C_{\text{avrp}}=\left[\begin{array}{ccc}0& -M_{\text{inf}}& 0\\ 0& 0& C_{q,h}\\ 0& C_{q,h}^T& C_h\end{array}\right]\text{\hspace{1em}(2)}$$

$C_h$是一个$N_h\times N_h$的块，表示所有网格单元之间的连接成本。由于我们旨在找到最短的CP，网格单元对之间的路径长度被用作连接成本：

$$C_h(h_1,h_2)=C_h(h_2,h_1)=\text{Len}[P(C_h(h_1,h_2))],h_1,h_2\in [1,N_h]\text{\hspace{1em}(3)}$$

这里，$c_{h1}$和$c_{h2}$分别表示$h_1$和$h_2$单元中未知体素的质心，而$P(c_{h1},c_{h2})$是两者之间的无碰撞路径，可以通过标准路径搜索算法找到。

四旋翼和网格单元之间的连接成本由$C_{q,h}$表示，这是一个$2\times N_h$的矩阵。连接成本类似于公式(3)，但添加了一个一致性项：

$$C_{q,h}(i,h)=\text{len}[P(q_i,c_h)]+c_{con}(i,h)h\in [1,N_h],i\in [1,2]\text{\hspace{1em}(4)}$$

其中一致性项$c_{con}$的定义为：

$$c_{con}(i,h)=\{\begin{array}{ll}{\beta }_{\text{con}},& \text{如果}{q}_i\text{直接连接到}h\text{单元}\\ 0,& \text{其他情况}\end{array}\text{\hspace{1em}(5)}$$

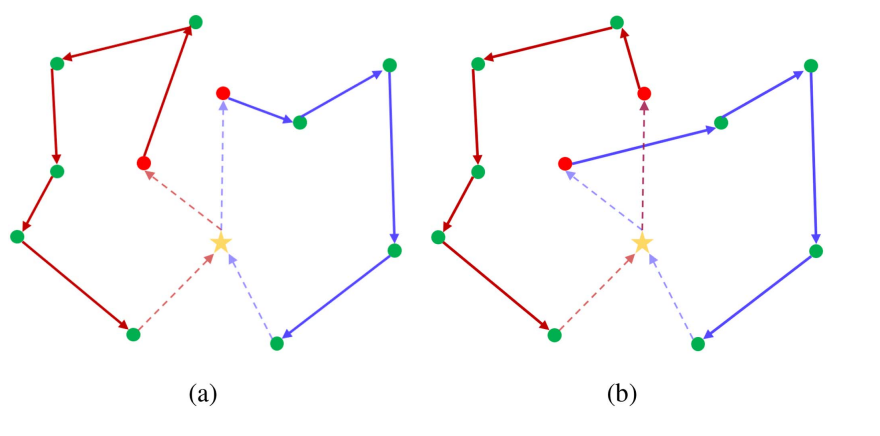
已经观察到，有时存在多个解，它们的路径长度相近，但覆盖路径不同（见图4）。因此，引入$c_{con}(\cdot )$来防止路径在不同模式间频繁变化，从而导致不一致的运动，进而减缓探索过程。

为了将问题转化为非对称的VRP，虚拟仓库到两个四旋翼的连接成本被分配为块$-M_{\text{inf}}=-[M_{\text{inf}},M_{\text{inf}}]$，其中$M_{\text{inf}}$是一个非常大的值。大负成本使得虚拟仓库的节点不直接连接两个四旋翼，因为它极大地减少了输出路径的总成本。这样，非对称VRP的输出包含期望的最短路径和四条额外的边，其中两条边将仓库与四旋翼连接，而另外两条边将两个单元连接到仓库。将我们的任务转化为非对称VRP的过程如图4所示。

2. 容量约束：尽管路径长度经过优化，但每个四旋翼探索的未知区域的实际数量并未考虑，这仍然可能导致负载不平衡。
   
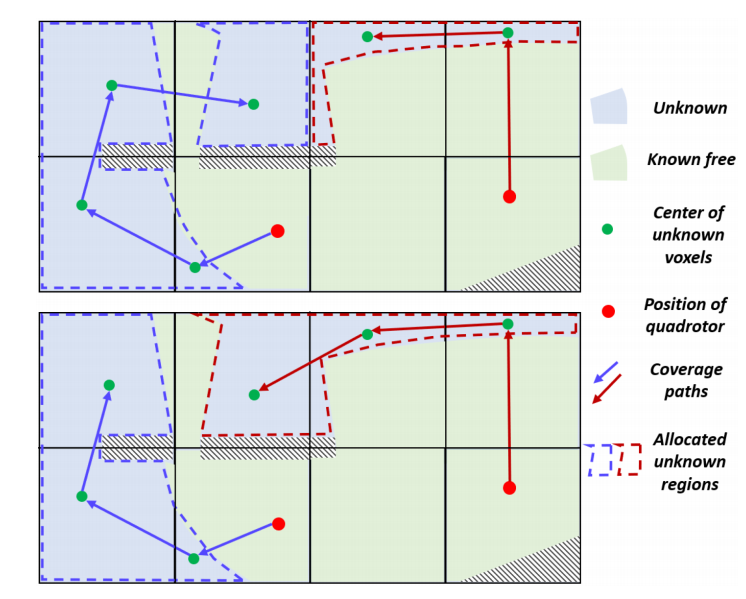
   图4. 非对称VRP的示意图。与虚拟仓库、四旋翼和网格单元相关的节点分别用黄色星形、红色圆圈和绿色圆圈表示。依次连接的红色和紫色边表示两条最小化总体成本的路径。 (a) 和 (b) 是两个具有相同成本的替代解。所需的CP通过移除与虚拟仓库连接的边（虚线显示）来获得。

图5. 两个四旋翼的CP及其对应的未知空间分配。顶部：仅考虑了总路径长度。未知空间的分配不平衡，其中红色的部分可以更快地被完全探索。底部：通过引入容量约束，两个四旋翼的工作负载更加均衡。

为了进一步平衡分配给四旋翼的工作负载，我们引入了容量约束。对于每个在VRP中的网格单元${\nu }_k$（假设为$h_k$单元），如果它与一个网格单元相关联，则分配给它的需求${\rho }_k$等于该单元中未知体素的数量$u_{h_k}$。否则，需求为零。我们将每个四旋翼的容量限制为未知体素总数的一个百分比。记四旋翼$q_i$路径中的节点集合为$R_i$，容量约束为：

$$\sum _{{\nu }_k\in R_i}{\rho }_k\le {\alpha }_{\rho }\sum _{h=1}^{N_h}{u}_h,i=1,2\text{\hspace{1em}(6)}$$

B. 稀疏图路径搜索

CVRP中的主要开销是计算$C_h$和$C_{q,h}$，这需要$O(N_h^2)$的路径搜索。在大规模环境中，当需要搜索大量全局路径时，这将变得非常昂贵，因为路径需要直接在体积地图上进行搜索。我们借鉴了[24]和[83]的灵感来减轻这种计算负担。具体来说，维护一个嵌入网格中的稀疏图，用于执行全局路径搜索。对于每个网格单元，附加一个图节点，并将每个相邻单元的节点连接到该节点，若两个单元之间存在无碰撞路径，则连接边权重为路径长度。
每当网格单元更新时，更新该单元到体积地图中的路径。如果找到解决方案，边的权重将更新为路径长度；否则，边将从图中移除。利用这个稀疏图，可以更容易地计算网格单元和四旋翼之间的连接成本。对于每一对网格单元，路径在稀疏图中被搜索，用来逼近在体积地图上的最短路径。对于一个远离四旋翼的网格单元，其成本通过四旋翼到最近网格单元的路径长度加上这两个网格单元之间的路径长度来近似。在实践中，近似成本导致的CVRP解与使用精确成本的解非常相似，但大大减少了计算时间。

VI. 探索规划

探索规划方法基于[1]，该方法增量式地提取前沿信息结构（FISs），并在多个层次上规划运动。在这项工作中，我们将该方法扩展到多四旋翼系统，允许有效且可扩展的团队探索。我们还通过将CP作为高层次指导，显著提高探索速率，从而扩展了探索规划。同时，我们还考虑了间歇性通信下的碰撞避免。探索规划的关键组件如图6所示。

A. 增量式FIS

为了促进探索规划，我们采用[1]中的方法来增量式地检测前沿[6]，这些前沿是与未知体素相邻的已知自由体素。检测到的前沿被分组到集群中，随后提取集群的位置信息（见算法3）。该过程的总结和更多细节请参见[1]。该方法通过移除更新地图中的过时前沿集群开始，其中首先使用集群的AABBs进行快速筛选，然后再进行详细检查（第1-4行）。接着，搜索新的集群，传感器噪声形成的集群会被过滤，大集群被分割成更小的集群，每个小集群都可以被一个视点覆盖（第5-9行）。

对于每个前沿集群$F_i$，计算其质心（第12行），而视点均匀采样（第13行），每个视点$q_{i,j}$由位置和偏航角$ya{w}^2$表示，$[p_{i,j},{\varphi }_{i,j}]$表示视点的位置和偏航角。具有足够覆盖集群的视点按覆盖度递减的顺序排序在$V_{F}i$中，保留前$N_{V}F$个视点（第14行）。最后，计算集群对之间的连接成本，以帮助进行探索规划（见第VI-B节）。对于两个视点$q_{k1,j1}$和$q_{k2,j2}$，在移动它们之间时的最小时间下界估算为：

$$t_{lb}(q_{k1,j1},q_{k2,j2})=\max \left(\frac{\text{Len}[P(p_{k1,j1},p_{k2,j2})]}{v_{\text{max}}}\right)\ast \min \left(\left|{\varphi }_{k1,j1}-{\varphi }_{k2,j2}\right|,2\pi -\left|{\varphi }_{k1,j1}-{\varphi }_{k2,j2}\right|\right)\frac{1}{{\varphi }_{\text{max}}}\text{\hspace{1em}(7)}$$

其中$\text{Len}(P(\cdot ))$是无碰撞路径的长度，$v_{\text{max}}$和${\varphi }_{\text{max}}$分别是最大速度和偏航角速度。集群$F_{k1}$和$F_{k2}$之间的连接成本由下式给出：$t_{lb}(q_{k1,j1},q_{k2,j2})$与[1]不同，针对多四旋翼系统做了一些适应性修改。除了仅计算由四旋翼更新的地图区域内的前沿信息结构（FISs）外，还应考虑到由邻近四旋翼共享的区域，以便不断保持完整的前沿列表。共享区域由四旋翼持续跟踪，并通过AABBs$B_m$（如第IV-B节所述）进行增量更新。与单一四旋翼相比，检测到更多的集群，从而在提取所有集群信息时造成了显著的计算负担。为了解决这个问题，我们通过将集群存储在四旋翼分配的工作区域内外的两个单独列表$F_a$和$F_s$（第10行）中来减轻负担。信息仅从$F_a$中的集群中提取，这不会对探索规划产生影响。如果分配的区域在交互后发生变化（见第IV-C节），相关的集群会根据情况重新分配到这两个列表中。

B. 分层规划

我们之前的方法[1]采用了一个分层规划管道，与最近的方法相比显著提高了探索速率[13]。然而，它没有考虑全局覆盖路径，因此四旋翼可能会重新访问相同的区域，导致性能下降。为了进一步提高效率，我们利用全局CP来引导探索规划，从而使四旋翼按更合理的顺序访问不同的区域。

1. CP引导的探索路径规划：在第V-A节中，CVRP输出分配给每个四旋翼的网格单元的CP。当网格更新时，我们重新计算CP来引导探索规划。对于下一个$N_{C}P$网格单元，我们定义前沿集群，其中质心位于该单元内。然后，找到一条从四旋翼当前视点开始的路径，访问每个集群，并以第$(N_{C}P+1)$个网格单元的质心为终点，如图7所示。受到[22]的启发，该问题被形式化为TSP的变种，具有固定的起点和终点。由于TSP是VRP的特例（车辆数量为1），因此可以采用与第V-A节相同的求解方法，只是需要考虑引入的额外约束，即考虑第$(N_{C}P+1)$个网格单元的终点。

假设有$N_f$个集群，参与的TSP包含$N_f+3$个节点，其中$N_f$是网格单元的节点数，3个节点分别表示虚拟仓库、四旋翼和网格单元。成本矩阵$C_{\text{TSP}}\in {\mathbb{R}}^{(N_f+3)\times (N_f+3)}$如下所示：

$$C_{\text{TSP}}=\left[\begin{array}{ccc}0& -M_{\text{inf}}& 0\\ 0& 0& C_{q,f}\\ 0& C_{q,f}^T& C_{h,f}\end{array}\right]\text{\hspace{1em}(8)}$$

图7. CP引导的路径规划示意图。 (a) 子划分未知空间的样本CP。 (b) 计算局部路径以覆盖沿CP的前沿集群（$N_{CP}=3$）。

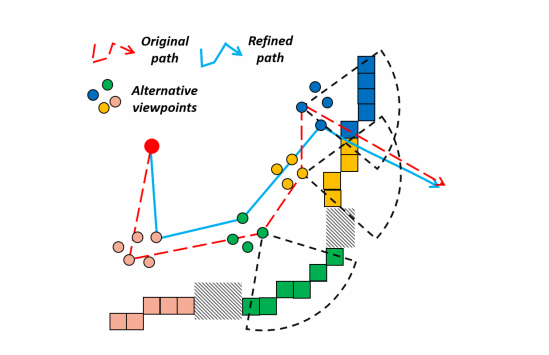
图8. 基于图搜索方法的局部视点优化。在局部探索路径上，考虑了每个前沿集群的替代视点，进一步提高路径质量。

$C_f$是记录集群之间连接成本的主要对称块，其条目通过以下公式计算：

$$C_f(k_1,k_2)=t_{lb}(q_{k1,1},q_{k2,1}),k_1,k_2\in [1,N_f]\text{\hspace{1em}(9)}$$

与网格单元的成本（公式(3)）不同，公式(9)不仅考虑了平移距离，还考虑了偏航角的变化。由于这些成本在提取新前沿集群时已经预先计算（见第VI-A节），因此可以无额外开销地填充$C_f$：$C_{q,f}\in {\mathbb{R}}^{1\times N_f}$是从当前视点$q_0=(p_0,{\phi }_0)$到$N_f$个集群的成本：
$$C_{q,f}(k)=t_{lb}(q_{k1},q_{k1})+w_{\text{con}}\cdot t_{\text{con}}(q_{k1},k),k\in [1,N_{\text{cls}}]\text{\hspace{1em}(10)}$$

$$t_{\text{con}}(q_k,j)=\{\begin{array}{ll}{\cos }^{-1}\left(\frac{(p_k,j-P_0)\cdot v_0}{|p_k,j-P_0|\cdot |Poll|}\right),& v_0\ne 0\\ 0,& \text{否则}\end{array}\text{\hspace{1em}(11)}$$

其中$v_0$是当前速度，$t_{\text{con}}(\cdot )$惩罚了航向角变化的增加，以促进更加一致的运动，类似于公式(5)。四旋翼和网格单元之间的连接成本通过$C_h$计算，其公式为：

$$C_h(k)=\text{Len}[P(p_k,k_{\text{NCP}}+1)]/v_{\text{max}}\text{\hspace{1em}(12)}$$

我们通过引入一个巨大的负数$-M_{\text{inf}}$来将TSP变体转化为标准形式，该值分配给虚拟仓库和四旋翼之间的所有连接，如网格单元和虚拟仓库之间的连接。它确保在输出路径中，仓库的节点和网格单元的节点是相邻的，如下所示。

2. 局部视点优化：一个有希望的初始路径是使用CP引导的路径规划生成的。然而，这条路径仅考虑了每个集群的单一视点，尽管可能存在多个视点。为了进一步提高路径的质量，使用了基于图的视点优化方法[1]。该方法通过考虑四旋翼当前的视点、每个集群的视点以及初始路径上的网格单元来生成有向无环图。该图捕捉了沿初始路径的所有可能的视点组合。需要注意的是，为了结合CP的引导，额外的图节点被引入到下一个网格单元的探索中，这与原始方法不同。给定该图，采用Dijkstra算法来找到最优路径，从而最小化探索成本。该过程如图8所示。

3. 最小时间B样条轨迹生成：给定由离散视点组成的路径，生成一个可执行的连续时间轨迹是必需的。我们基于[1]和[66]中的轨迹生成方法，生成平滑、安全和动态可行的B样条轨迹，以确保实时性。我们进一步考虑了四旋翼之间的碰撞避免问题。

四旋翼的微分平坦性[84]允许我们生成简单的轨迹，以便进行平面输出$q\in (x,y,z,\phi )$。对于每个四旋翼$q_i$，我们找到统一的B样条轨迹${\Psi }_{b,i}(t)=(p_b(t),{\phi }_b(t))$，其最小化平滑性成本和总轨迹时间，同时满足安全性、动态可行性和边界状态的约束。B样条的度为$N_b$，由一组控制点 Q c , b = { q c 0 , q c 1 , … , q c N b } Q_{c,b} = \{qc_0, qc_1, \dots, qc_{N_b} \} Qc,b​={qc0​,qc1​,…,qcNb​​}定义，其中$q{c}_m=(p_{c,m},{\phi }_{c,m})$，并具有一个节点跨度$\Delta t_b$。优化问题被公式化，以求解期望的解：

$$\arg \min J_s+w_{t}T+{\lambda }_c\left(J_{c}o+J_{c}q\right)+{\lambda }_d\left(J_v+J_a\right)+{\lambda }_{bs}{J}_{bs}$$

其中，$J_s$是弹性带平滑性成本，$T$是总轨迹时间，$J_{c}o$和$J_{c}q$是四旋翼与其他四旋翼的碰撞惩罚，$J_v$和$J_a$是动态可行性约束，$J_{bs}$是边界状态约束，表示瞬时状态$(q_0,\dot{q_0},\ddot{q_0})$的约束。

和第VI-B2节中获得的目标视点相似。该方法已被证明可以在实时中找到高质量的轨迹，并且能够支持在复杂环境中进行单一四旋翼的高速导航。详细的公式化可以在[1]中找到，这里给出了多四旋翼碰撞避免项$J_{c,q}$的具体定义。

对于四旋翼避开附近四旋翼的碰撞，涉及其轨迹${\Psi }_{b,j}(t),q_j\in Q_n$。强制执行四旋翼$q_i$和每个$q_j$之间的距离，类似于[76]：

$$J_{c,q}=\sum _{q_j\in Q_n}\sum _{k=1}^{T/\delta t_q}J(d_{q,j}(T_k),d_{\text{min},q})\text{\hspace{1em}(13)}$$

$$d_{q,j}(t)=\Vert \mathbf{E}\frac{1}{2}[{\Psi }_{b,i}(t)-{\Psi }_{b,j}(t)]\Vert \text{\hspace{1em}(14)}$$

其中，$T_k=T_s+k\delta t_q$，$T_s$是${\Psi }_{b,i}(t)$的起始时间，$\mathbf{E}=\text{diag}(1,1,{\beta }_q)$，${\beta }_q<1$将欧氏距离转换为考虑四旋翼下洗效应的距离。轨迹生成也是以去中心化的方式进行的，并且发生频率比[1]中的更高。除了在每次新探索路径计算后规划新轨迹外，每个四旋翼还通过广播共享其最新轨迹。若四旋翼接收到来自其他四旋翼的轨迹并检测到碰撞，它立即生成一条新轨迹来避开碰撞，同时仍到达新的目标视点。轨迹的持续交换确保了在通信延迟或数据包丢失情况下的安全性。有关该互惠碰撞避免的更全面分析，请参见[76]。