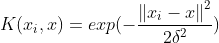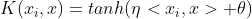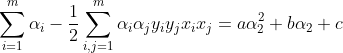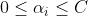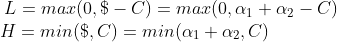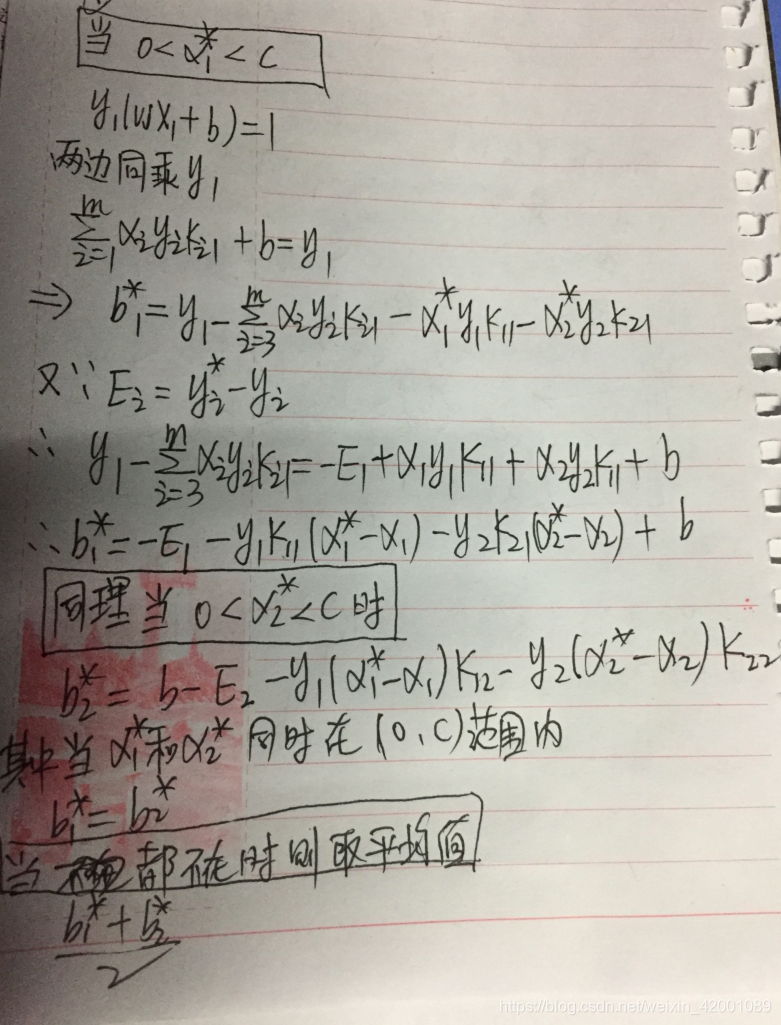笔者在查阅了大量资料和阅读大佬的讲解之后,终于对svm有了比较深一点的认识,先将理解的推导过程分享如下:
本文主要从如下五个方面进行介绍:基本推导,松弛因子,核函数,SMO算法,小结五个方面以%%为分隔,同时有些地方需要解释或者注意一下即在画有---------符号的部分内。
本文主要介绍的是理论,并没有涉及到代码,关于代码的具体实现,可以在阅读完本文,掌握了SVM算法的核心内容后去看一下笔者另一篇SVM代码剖析:
https://blog.csdn.net/weixin_42001089/article/details/83420109
%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%
基本推导
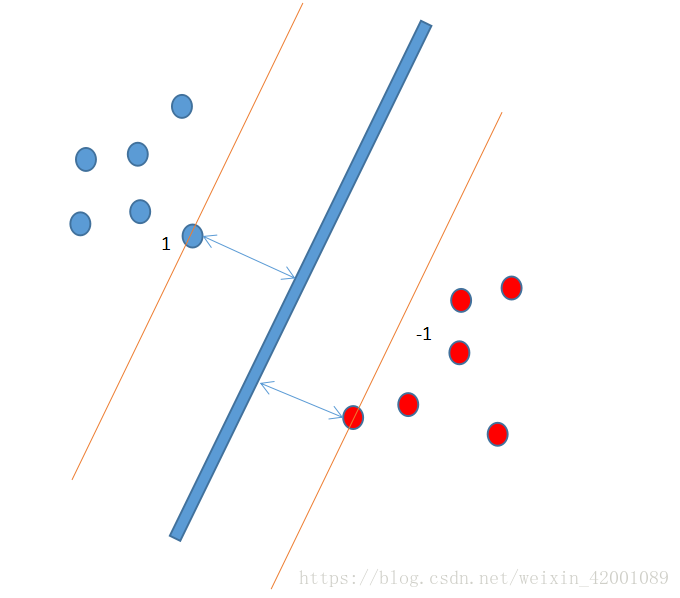
svm原理并不难理解,其可以归结为一句话,就是最大化离超平面最近点(支持向量)到该平面的距离。
如下图
开门见山就是下面的最值优化问题:
注意
(1)这里的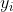 就是标签假设这里是二分类问题,其值是1和-1,其保证了不论样本属于哪一类
就是标签假设这里是二分类问题,其值是1和-1,其保证了不论样本属于哪一类 都是大于0的
都是大于0的
(2) 称为函数距离,
称为函数距离,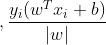 称为几何距离,这里之所以要使用几何距离是因为,当
称为几何距离,这里之所以要使用几何距离是因为,当 成倍增加时,函数距离也会相应的成倍的增加,而几何函数则不会
成倍增加时,函数距离也会相应的成倍的增加,而几何函数则不会
这里涉及到求两个最值问题,比较棘手,正如上面所说,几何距离不受成倍增加的影响,这里不妨就将最近点到超平面的函数距离设为1,自然其他非最近点的函数距离便是大于1,于是以上问题转化为:
这是一个在有不等式约束下,最小值优化的问题,这里可以使用kkt条件
--------------------------------------------------------------------------------------------------------------------------------------------------------------------
这里简单介绍一下kkt和拉格朗日乘子法(一般是用来求解最小值的优化问题的)
在求优化问题的时候,可以分为有约束和无约束两种情况。
针对有约束的情况又有两种情况即约束条件是等式或者是不等式
当是等式的时候:
首先写出其拉格朗日函数:
需满足的条件是:
而当约束条件是不等式时,便可以使用kkt条件,其实kkt条件就是拉格朗日乘子法的泛化
同理首先写出拉格朗日函数:
好了,接着往下走介绍拉格朗日对偶性:
上面问题可以转化为(称为原始问题):
为什么可以转化呢?这里是最难理解的:笔者还没有完全透彻的理解,这里试着解释一下吧,也是网上最流行的解释方法:
这里分两种情况进行讨论:
当g(x)或者h(x)不满足约束条件时:
那么显然: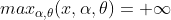
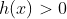
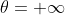
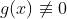

当g(x)或者h(x)满足约束条件时:
综上所述:
所以如果考虑极小值问题那么就可以转化为:
还有一种比较直观的方法,这里不再证明,可以参考:如何通俗地讲解对偶问题?尤其是拉格朗日对偶lagrangian duality? - 知乎第二个回答
对偶问题:
上面关于拉格朗日最小最大值问题可以转化为求其对偶问题解决:
两者关系:
假设原始问题的最优解是

即其对偶问题的解小于等于原始问题的解,现在我们要通过其对偶问题来求的原始问题的解对吧,所以我们希望的是
那么什么时候才能相等呢?这就必须满足的kkt条件:
-----------------------------------------------------------------------------------------------------------------------------------------------------------------
说了这么多拉格朗日的东西,其实其本质作用就是,将有不等式约束问题转化为无约束问题(极小极大值问题),然后又进一步在满足kkt条件下将问题转化为了其对偶问题,使之更容易求解,下面要用到的就是上面紫色的部分,关于更深的拉格朗日求解问题大家可以去收集资料参看。
对应到SVM的拉格朗日函数便是:
-----------------------------------------------------------------------------------------------------------------------------------------------------------
注意上面给的不等式约束是
----------------------------------------------------------------------------------------------------------------------------------------------------------
于是问题转化为:
根据对偶转化:
好啦,这里没什么说的就是根据kkt条件求偏导令其为0:
于是就得到:
将上述两公式带入到 如下:
如下:
于是问题转化为:
所以最后就得出这样的步骤:
1首先根据上面的最优化问题求出一些列的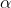
2然后求出w和b
所以当一个样本进来的时候即值便是:
3根据如下进行分类:
%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%
松弛因子
上面是SVM最基本的推导,下面说一下这种情况就是有一个点由于采集错误或者其他原因,导致其位置落在了别的离别当中,而svm是找最近的点,所以这时候找出的超平面就会过拟合,解决的办法就是忽略掉这些点(离群点),即假如松弛因子 ,使几何距离不那么大于1
,使几何距离不那么大于1
数学化后的约束条件即变为:
这里简单来理解一些C的含义:这是一个在使用SVM时需要调的参数,


接下来还是使用上面拉格朗日对偶问题进行求解,这里就不详细说明了,直接给出过程:
令
求导令其为0:
将其带入最终问题可得:
---------------------------------------------------------------------------------------------------------------------------------------------------------------------
这里得到的和没加松弛变量时是一样的
------------------------------------------------------------------------------------------------------------------------------------------------
对应的kkt条件为:
注意如下几点:
一:对比最开始的kkt条件模板
这里的(1)(8)(9)是求偏导的结果即一二三公式,(6)(7)是拉格朗日乘子即相当于模板的第五公式,(2)(4)相当于模板第六个公式,(3)(5)是原始约束条件即相当于模板的第七个公式
二:可以将kkt中部分条件进行总结归纳:(6)(7)(8)三个条件:
所以可以总结为:
可以看到这里和没加松弛变量相比,唯一不同的就是
三:说一下 取不同值时意义
取不同值时意义
对比模板
当
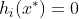
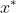
当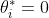

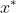
当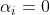 时:
时:
由(8)可得:
又有公式(4)可得:
最后又公式(3)可得:
当 时:
时:
同理
又(2)可得:
最后:
当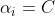 时:
时:
进而这里还是只能得到
最后:
综上所述可以总结为:
在点在两条间隔线外则,对应前面的系数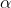
通过上面也可以看出,最后求出的所有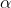
所以对应到松弛遍历这里的步骤就是:
1首先根据上面的最优化问题求出一些列的
2然后求出w和b
注意这里是随便取一个点i就可以算出b,但是实际中往往取所有点的平均
3得出超平面
注意这里说一下
%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%
核函数:
出现的背景:
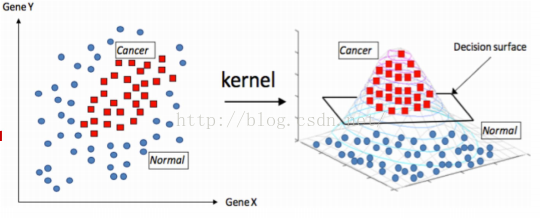
对于一些线性不可分的情况,比如一些数据混合在一起,我们可以将数据先映射到高纬,然后在使用svm找到当前高纬度的超平面,进而将数据进行有效的分离,一个直观的例子:
图片来源七月算法
比如原来是:
则现在为:
其中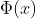 就是映射公式,即先映射到高纬再进行内积
就是映射公式,即先映射到高纬再进行内积
但是问题来了,那就是假设原始数据维度就好高,再进一步映射到高纬,那么最后的维度可能就非常之高,再进行内积等这一系列计算要求太高,很难计算。
因此我们可以令
这里的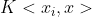 便是核函数,其意义在于我们不用去映射到高纬再内积,而是直接在低纬使用一种核函数计算
便是核函数,其意义在于我们不用去映射到高纬再内积,而是直接在低纬使用一种核函数计算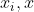 ,使其结果和映射到高纬再内积效果一样,这就是核函数的威力,大部分是内积,而SVM的奇妙之处就在于所有的运算都可以写成内积的形式,但是这种核函数具体该怎么选取呢?别慌,已经有前辈们帮我们找到了很多核函数,我们直接拿过来用就可以啦。
,使其结果和映射到高纬再内积效果一样,这就是核函数的威力,大部分是内积,而SVM的奇妙之处就在于所有的运算都可以写成内积的形式,但是这种核函数具体该怎么选取呢?别慌,已经有前辈们帮我们找到了很多核函数,我们直接拿过来用就可以啦。
下面介绍几种常见的吧:更多的大家可以自行查阅:
(1)线性核函数 :也是首选的用来测试效果的核函数
其维度与原来相同,主要用于线性可分的情况,其实就是原始导出的结果
(2)多项式核函数
其实现将低维的输入空间映射到高纬的特征空间,但多项式的阶数也不能太高,否则核矩阵的元素值将趋于无穷大或者无穷小,计算复杂度同样会大到无法计算。而且它还有一个缺点就是超参数过多
(3)径向基高斯(RBF)核函数
高斯(RBF)核函数核函数性能较好,适用于各种规模的数据点,而且参数要少,因此大多数情况下优先使用高斯核函数。
(4)sigmoid核函数
不难看出这里有点深度学习当中,一个简单的神经网络层
总的来说就是,当样本足够多时,维度也足够高即本身维度已经满足线性可分,那么可以考虑使用线性核函数,当样本足够多但是维度不高时,可以考虑认为的增加一定的维度,再使用线性核函数,当样本也不多,维度也不高时,这时候可以考虑使用高斯(RBF)核函数。
关于SVM ,python中有一个机器学习库sklearn,其中集成了很多机器学习方法,包括SVM,笔者这里也做过一个简单直观的调用,可以参看python_sklearn机器学习算法系列之SVM支持向量机算法_爱吃火锅的博客-CSDN博客
再者就是我们虽然可以直接拿sklearn库下集成好的接口来用,但是其具体实现细节,还是有必要了解一下,换句话说:
上面我们最后得到的结果是:
我们求出一些列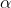
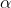
%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%
SMO算法
现在的问题是:
首先要明确我们的目的是求一些列的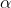 ,其思路也是很简单就是固定一个参数即以此为自变量,然后将其他的变量看成常数,只不过因为这里
,其思路也是很简单就是固定一个参数即以此为自变量,然后将其他的变量看成常数,只不过因为这里 约束条件,所以我们一次取出两个
约束条件,所以我们一次取出两个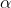 作为自变量进行优化,然后外面就是一个大的循环,不停的取不停的优化,知道达到某个条件(后面介绍)停止优化。
作为自变量进行优化,然后外面就是一个大的循环,不停的取不停的优化,知道达到某个条件(后面介绍)停止优化。
思路框架就是上面这么简单,下面来看一下理论方面的精确推导:
假设我们首先取出了 和
和 ,那么后面的便可以整体视为一个常数即:
,那么后面的便可以整体视为一个常数即:
先将 用
用 表示出来,也很简单:
表示出来,也很简单:
带入到原始优化的目标方程中可得:
即关于 的一元二次方程(其中a,b,c都是常数)
的一元二次方程(其中a,b,c都是常数)
--------------------------------------------------------------------------------------------------------------------------------------------------------------
为什么是二元一次方程呢?很简单由原始优化目标可以看出基本单元就是
-------------------------------------------------------------------------------------------------------------------------------------------------------------
好啦,求一元二次方程最值应该很简单啦吧,即:
相应的根据 便可以求出
便可以求出
这样就完成啦一对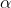 值的优化,接着找下一对
值的优化,接着找下一对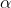 值就行优化即可
值就行优化即可
-------------------------------------------------------------------------------------------------------------------------------------------------------------
介绍到这里也许会发现还有一个约束条件没有用即:
是的我们在算
回到:
我们分类讨论:
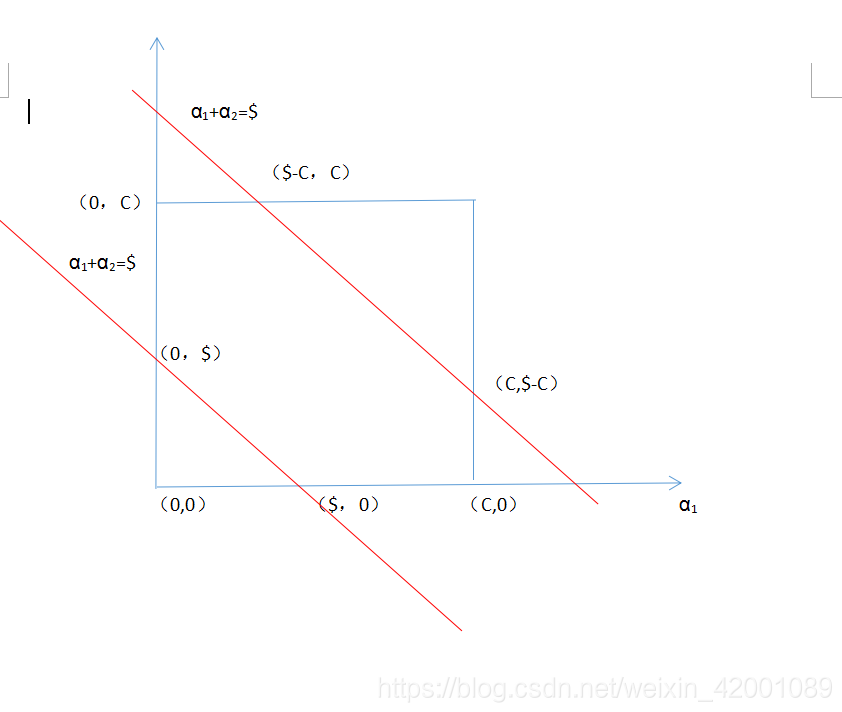
(1)当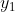
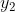
则是一个斜率为-1的直线即
那么可以画出如下图。横坐标是

现在要保证范围,即
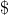
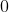
所以最后综合一下即
(2)当当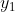
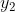
则是一个斜率为1的直线即
那么可以画出如下图。横坐标是

现在要保证范围,即

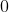
所以最后综合一下即
所以在我们通过一元二次方程求得的

注意这里有时候L=H这代表
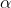
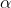
--------------------------------------------------------------------------------------------------------------------------------------------------------------
好的我们接着往下走,刚才说得到一个一元二次方程组那么系数a,b,c是多少呢?我们来求一下:
我们先将 和
和 带入:
带入:
公式太多就不用编辑器啦,字迹有点潦草==
现在我们进一步化简一下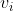 :
:
我们将本次要优化的参数标为*即规范一下就是:
相对应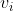 中的
中的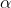 没有*就代表使用上次结果的
没有*就代表使用上次结果的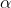
好啦接下来要做的就像上面说的用 表达式代替
表达式代替 ,然后求导为0
,然后求导为0
最后我们要的结果就是红框的部分(其中 )
)
将w,v都带入便得到:
注意这里的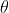
因为下面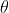

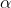
关于b的更新需要根据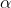 的取值来进行判断:
的取值来进行判断:
好啦,最最最最最最重要的一张图来啦,也是我们上面花了这么多力气得出的结果,也是我们最终程序设计的蓝图:
%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%
最后小结理一下思路:
求解过程:
首先我们要优化的问题是:
然后利用拉格朗日对偶问题将问题转化为:
接着我们使用了SMO算法求解出了一系列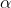
核函数:
将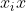
%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%
看到很多小伙伴私信和关注,为了不迷路,欢迎大家关注笔者的微信公众号,会定期发一些关于NLP的干活总结和实践心得,当然别的方向也会发,一起学习:
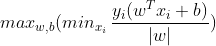
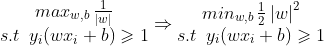
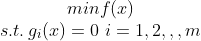
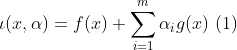

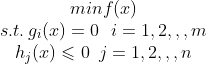

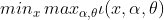
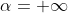






![\iota (w,b,\alpha )=\frac{1}{2}\left | w \right |^{2}{\color{Red} -}\sum_{i=1}^{m}\alpha _{i}\left [ y_{i}(w^{T}x_{i}+b)-1 \right ]](/image/aHR0cHM6Ly9wcml2YXRlLmNvZGVjb2dzLmNvbS9naWYubGF0ZXg%2FJTVDaW90YSUyMCUyOHclMkNiJTJDJTVDYWxwaGElMjAlMjk%3D%3D%5Cfrac%7B1%7D%7B2%7D%5Cleft%20%7C%20w%20%5Cright%20%7C%5E%7B2%7D%7B%5Ccolor%7BRed%7D%20-%7D%5Csum_%7Bi%3D1%7D%5E%7Bm%7D%5Calpha%20_%7Bi%7D%5Cleft%20%5B%20y_%7Bi%7D%28w%5E%7BT%7Dx_%7Bi%7D+b%29-1%20%5Cright%20%5D)








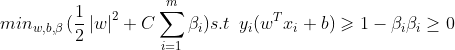








![\alpha _{i}\left [ y_{i}y(x) -(1-\beta _{i})\right ]=0\, \, \, \, (2)](/image/aHR0cHM6Ly9pLWJsb2cuY3NkbmltZy5jbi9ibG9nX21pZ3JhdGUvZGViYWY0NWIyYTEzMTg1YmNhZGE1NjAxODQ0YTU5YmMuZ2lm%20_%7Bi%7D%5Cleft%20%5B%20y_%7Bi%7Dy%28x%29%20-%281-%5Cbeta%20_%7Bi%7D%29%5Cright%20%5D%3D0%5C%2C%20%5C%2C%20%5C%2C%20%5C%2C%20%282%29)
![\left [ y_{i}y(x) -(1-\beta _{i})\right ]\geq 0\, \, \, \, (3)](/image/aHR0cHM6Ly9wcml2YXRlLmNvZGVjb2dzLmNvbS9naWYubGF0ZXg%2F%5Cleft%20%5B%20y_%7Bi%7Dy%28x%29%20-%281-%5Cbeta%20_%7Bi%7D%29%5Cright%20%5D%5Cgeq%200%5C%2C%20%5C%2C%20%5C%2C%20%5C%2C%20%283%29)








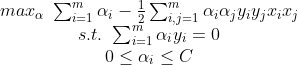
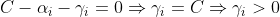
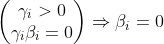
![\left [ y_{i}y(x) -(1-\beta _{i})\right ]\geq 0\Rightarrow y_{i}y(x) \geq 1](/image/aHR0cHM6Ly9pLWJsb2cuY3NkbmltZy5jbi9ibG9nX21pZ3JhdGUvNDYwNTNiYzk1YTlmYTFmYjJlMTU1MmFjNjFhMzMzN2EuZ2lm)

![\begin{pmatrix} \alpha _{i}\left [ y_{i}y(x) -(1-\beta _{i})\right ]=0\\ 0< \alpha _{i}< C \end{pmatrix}\Rightarrow \left [ y_{i}y(x) -(1-\beta _{i})\right ]=0](/image/aHR0cHM6Ly9pLWJsb2cuY3NkbmltZy5jbi9ibG9nX21pZ3JhdGUvM2FlZTUyNDkzNTNmMmVhMDg1MjdhYzBiZmEwMDg1YWEuZ2lm)


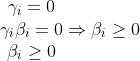
![\left [ y_{i}y(x) -(1-\beta _{i})\right ]\geq 0\Rightarrow y_{i}y(x) \geq (1-\beta _{i})](/image/aHR0cHM6Ly9pLWJsb2cuY3NkbmltZy5jbi9ibG9nX21pZ3JhdGUvMTAwNzg0OGZlNjQ3MzliZTFjODA2ODk0ZDdjODE0MTcuZ2lm)

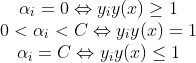
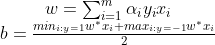
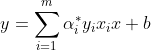


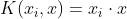
![K(x_{i},x)=[(x_{i}\cdot x)+1]^{m}](/image/aHR0cHM6Ly9wcml2YXRlLmNvZGVjb2dzLmNvbS9naWYubGF0ZXg%2FK%28x_%7Bi%7D%2Cx%29%3D%5B%28x_%7Bi%7D%5Ccdot%20x%29+1%5D%5E%7Bm%7D)