Multiple Instance Detection Network with Online Instance Classifier Refinement

华中科大Peng Tang, Xinggang Wang CVPR, 2017 (PDF) (code)

Contributions

1. We propose a framework for weakly supervised learning that combines MIDN with multi-stage instance classifiers. With only supervision of the outputs from its preceding stage, the discriminatory power of the instance classifier can be enhanced iteratively.

2. We further design a novel OICR algorithm that integrates the basic detection network and the multi-stage instance-level classifier into a single network. The proposed network is end-to-end trainable. Compared with the alternatively training strategy, we demonstrate that our method can not only reduce the training time, but also boost the performance.

3. Our method achieves significantly better results over previous state-of-the-art methods on the challenging PASCAL VOC 2007 and 2012 benchmarks for weakly supervised object detection.

Method

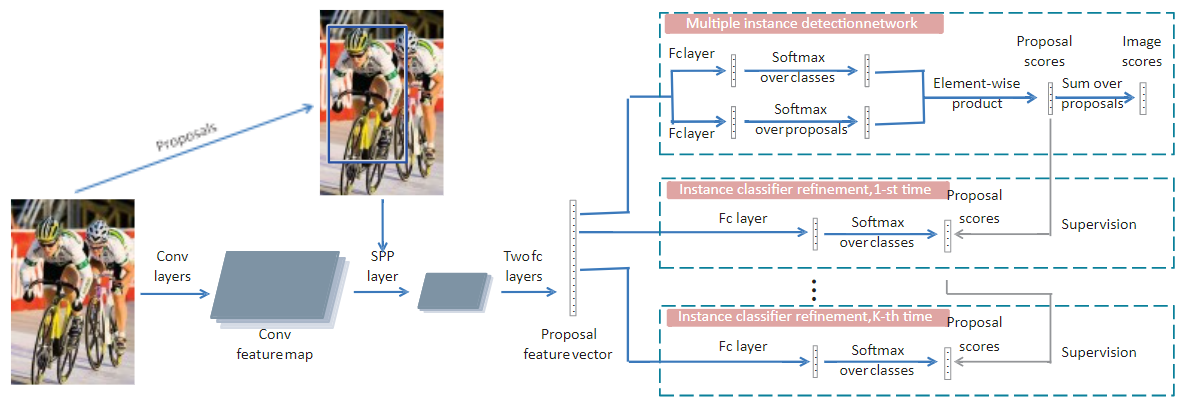
MIDN(Multiple instance detection network)

• Proposal feature vector 经过FC层分别得到 ${\mathbf{x}}^c，{\mathbf{x}}^d\in {\mathbb{R}}^{C\times |R|}$
• ${\mathbf{x}}^c$经过Sofrmax层得到${\left[\sigma \left({\mathbf{x}}^c\right)\right]}_{ij}=\frac{e^{x_{ij}^c}}{{\sum }_{k=1}^C{e}^{x_{kj}^c}}$, 表示建议区域$j$属于类别$i$的概率。
• ${\mathbf{x}}^d$经过Sofrmax层得到${\left[\sigma \left({\mathbf{x}}^d\right)\right]}_{ij}=\frac{e^{x_{ij}^c}}{{\sum }_{k=1}^{|R|}{e}^{x_{ik}^c}}$, 表示图片被分类为$i$类时建议区域$j$作的贡献。
• 初始建议得分矩阵${\mathbf{x}}^R=\sigma \left({\mathbf{x}}^c\right)\odot \sigma \left({\mathbf{x}}^d\right)$，其中每个元素 $x_{ij}^R$ 表示建议区域 $r_j$ 对类别$i$的得分，用于后续迭代。
• 对所有区域建议求和得到图像分数${\varphi }_c={\sum }_{r=1}^{|R|}{x}_{cr}^R$，表示图像对类别$c$的得分。
• 基本实例分类器多类交叉熵损失函数 L b = − ∑ c = 1 C { y c log ⁡ ϕ c + ( 1 − y c ) log ⁡ ( 1 − ϕ c ) } \mathrm{L}_{\mathrm{b}}=-\sum_{c=1}^{C}\left\{y_{c} \log \phi_{c}+\left(1-y_{c}\right) \log \left(1-\phi_{c}\right)\right\} Lb​=−∑c=1C​{yc​logϕc​+(1−yc​)log(1−ϕc​)}

OICR(Online instance classifier refinement)

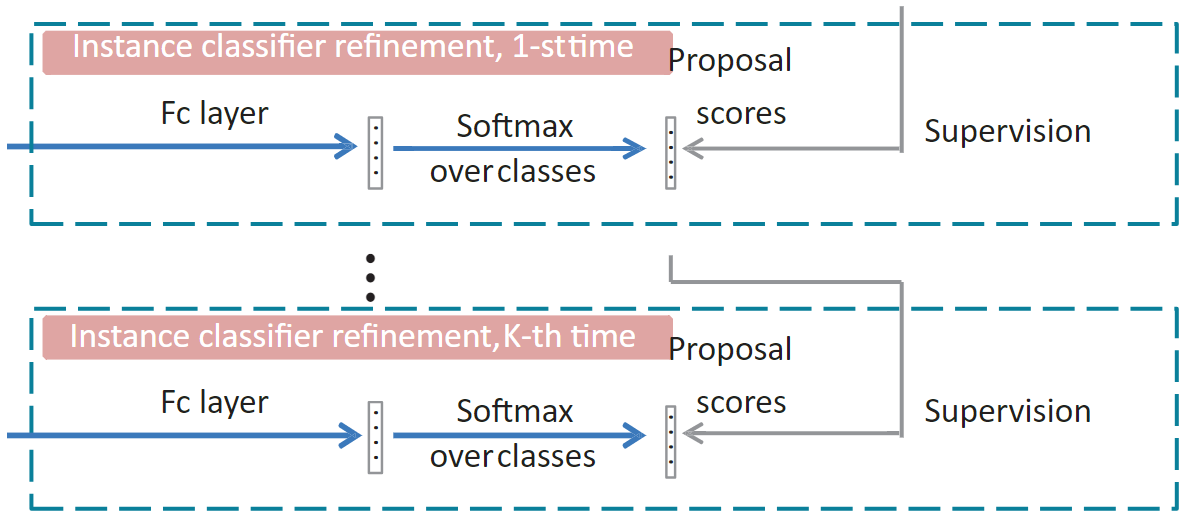
精炼分类器的一种自然方式是一种交替策略，即固定分类器并标记提议，固定提议标签并训练分类器。但它有一些局限性：1）非常耗时，因为它需要多次训练分类器； 2）在不同的细化步骤中分别训练不同的分类器可能会损害性能，因为它阻碍了从共享表示中受益的过程。因此，我们将基本的 MIDN 和不同的分类器精炼阶段集成到一个网络中，并对其进行端到端的训练。

通过利用 $WSDDN$ 作为初始定位网络，逐步训练多个实例分类器以细化定位结果并获得性能良好的检测器。这里，设 $K$ 是实例分类器的数量，${\text{x}}^{Rk}\in R^{(C+1)\times |R|}$ 是第 $k$ 个实例分类器的输出建议得分。与 ${\text{x}}^R$ 不同，${\text{x}}^{Rk}(k\in 1,...,K)$ 具有第 { C + 1 } \{C +1\} {C+1} 个背景维度。为了逐步训练多实例分类器，第 $k$ 个实例分类器的真实标签 由最后一个实例分${\text{x}}^{Rk}\in R^{(C+1)\times |R|}$ 类器的输出 ${\text{x}}^{R(k-1)}$ 制成。基于 ${\text{y}}^k$，训练每个实例分类器以最小化以下损失：
$$L_r^k=-\frac{1}{|R|}\sum _{j=1}^{|R|}\sum _{c=1}^{C+1}{y}_{cj}^k\log x_{cj}^k$$

在 $OICR$ 中，实例标注是如何从最后的定位结果 ${\text{x}}^{R(k-1)}$生成实例标签 ${\text{y}}^k$ 的问题。假设图像 $X$ 具有类标签 $c$，他们首先选择得分最高的区域建议 $r_{j_c}$，
$$j_c^{k-1}=\arg \underset{j}{\max }{x}_{cj}^{R(k-1)}$$
并受到高度重叠区域应具有相同标签这一事实的启发，制定了以下标签算法，

$$y_{cj}^k=\{\begin{array}{ll}1& \text{ if }\mathrm{IoU}\left(r_j^{k-1},r_{j_c}^{k-1}\right)>I_t\\ 0& \text{ otherwise }\end{array}$$
其中 $\mathrm{IoU}$ 是计算两个区域之间的交并比 ( $\mathrm{IoU}$ ) 的函数，$I_t$ 是一个阈值。当多个类满足 $\mathrm{IoU}\left(r_j^{k-1},r_{j_c}^{k-1}\right)>I_t$ 时，$y_{cj}^k$ 其 $c={\mathrm{a}\mathrm{r}\mathrm{g}\mathrm{m}\mathrm{a}\mathrm{x}}_{c^{\prime }}\mathrm{IoU}\left(r_j^{k-1},r_{j_c}^{k-1}\right)>I_t$ 为 $1$，其他为 $0$。如果一个区域没有分配任何对象类，即 $y_{cj}^k$ 为 $0$ 对于所有 c ∈ { 1 , . . . , C } c\in \{1, ..., C\} c∈{1,...,C}，该区域被标记为背景，
$$y_{(C+1)j}^k=1$$
但是，最后一个定位结果生成的标签是不可靠的，尤其是在训练开始时。这会导致训练的不稳定性。为了解决这个问题，方程中的损失函数。精炼的实例分类器损失函数改为加权版本如下，

$$w_j^k=x_{c{j}_c}^{k-1}$$
当图像具有多个类时，在上式, $c={\mathrm{a}\mathrm{r}\mathrm{g}\mathrm{m}\mathrm{a}\mathrm{x}}_{c^{\prime }}\mathrm{IoU}\left(r_j,r_{j_{c^{\prime }}}\right)>I_t$。在训练开始时或对于难以定位的图像，权重 $w_j^k$ 取低值，对训练的贡献变小。进而每一个精炼的实例分类器损失函数重写为加权版本：

$${\mathrm{L}}_{\mathrm{r}}^k=-\frac{1}{|R|}\sum _{r=1}^{|R|}\sum _{c=1}^{C+1}{w}_r^k{y}_{cr}^k\log x_{cr}^{Rk}$$

总损失函数如下：

$$\mathrm{L}={\mathrm{L}}_{\mathrm{b}}+\sum _{k=1}^K{\mathrm{L}}_r^k$$