文章目录
- 权重生成与评价模型(上)
- 1. 层次分析法
- 2. 熵权分析法
- 3. TOPSIS分析法
- 4. CRITIC方法
- 5. 一些奇奇怪怪的疑问
- 5.1 为什么熵权法计算权重的公式是 w j = 1 − e j ∑ j = 1 n ( 1 − e j ) w_j = \frac{1 - e_j}{\sum_{j=1}^n (1 - e_j)} wj=∑j=1n(1−ej)1−ej
- 5.2 熵权法的应用场景和局限性
- 5.3 **根据相对接近度排序**:根据 C i ∗ C_i^* Ci∗ 对各方案进行排序,值越大,方案越优。为什么不用 D i + D i + + D i − \frac{D_i^+}{D_i^+ + D_i^-} Di++Di−Di+来进行比较?
- 5.4 什么是皮尔逊相关系数,有什么应用
- 5.5 为什么**计算指标冲突性**:定义为: R j = ∑ i = 1 m ( 1 − r i j ) R_j = \sum_{i=1}^{m} (1 - r_{ij}) Rj=∑i=1m(1−rij)
权重生成与评价模型(上)
1. 层次分析法
层次分析法(Analytic Hierarchy Process, AHP)是一种多准则决策方法,广泛应用于复杂决策和规划问题中。它通过将决策问题分解成一个层次结构,然后通过一系列的比较对准则和备选方案进行评估,最终得到各备选方案的综合权重。
层次分析法的详细说明可参考:
1.1 层次分析法的原理
层次分析法的基本原理包括以下几个步骤:
-
建立层次结构:将决策问题分解成目标、准则和备选方案三个层次。顶层是决策目标,中间层是影响决策的准则,底层是具体的备选方案。
-
构建判断矩阵:通过两两比较的方式,对准则和备选方案进行相对重要性的评估,形成判断矩阵。
-
计算权重向量:从判断矩阵中计算各准则和备选方案的权重向量,即特征向量。
-
一致性检验:检查判断矩阵的一致性,确保比较结果的合理性。如果一致性通过,则计算最终的综合权重;否则需要调整判断矩阵。
构建判断矩阵
假设有 n n n 个准则(或备选方案),构建一个 n × n n \times n n×n 的判断矩阵 A A A,其中 a i j a_{ij} aij 表示第 i i i 个准则与第 j j j 个准则的相对重要性。矩阵 A A A 满足以下性质:
- a i j > 0 a_{ij} > 0 aij>0
- a i j × a j i = 1 a_{ij} \times a_{ji} = 1 aij×aji=1
-
a
i
i
=
1
a_{ii} = 1
aii=1
关于这个矩阵的每一项取值多少,若因素i比因素j重要,为了描述重要程度,我们用1~9中间的整数描述,如表5.2所示。
表1.1 重要性程度取值
| 取值 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 |
|---|---|---|---|---|---|---|---|---|---|
| 相对重要程度 | 同等重要 | 介于1、3之间 | 相对重要一些 | 介于3、5之间 | 相对比较重要 | 介于5、7之间 | 相比明显重要 | 介于7、9之间 | 相比非常重要 |
表1.1中描述的重要性是因素i比因素j重要的情况下描述的。如果是因素j比因素i重要,“相对不重要程度”那就用1~9的倒数描述即可。这个比较矩阵每一项的确定具有较强的主观性,因为究竟二者重要程度是比较重要还是非常重要也是不同的人可能有不同的理解,但总体来讲是奏效的。
注意:通常来说,对重要性的取值都是取奇数,也就是1、3、5、7、9,偶数是当你不太确定,也就是认为介于两个奇数程度之间时再取偶数。
除了准则层外,方案层也需要构建成对比较矩阵。但不同的是,假如有m个准则n个样本,需要构建的矩阵数量为m,矩阵大小为(n,n)。
权重向量计算
通过特征向量法,计算判断矩阵 A A A 的最大特征值 λ max \lambda_{\max} λmax 对应的特征向量 w \mathbf{w} w 作为权重向量。标准化后得到各准则(或备选方案)的权重。
一致性检验
一致性指标
C
I
CI
CI 和一致性比例
C
R
CR
CR 用于评估判断矩阵的一致性:
C
I
=
λ
max
−
n
n
−
1
CI = \frac{\lambda_{\max} - n}{n - 1}
CI=n−1λmax−n
C
R
=
C
I
R
I
CR = \frac{CI}{RI}
CR=RICI
其中,
R
I
RI
RI 为随机一致性指数,与矩阵的阶数有关。如果
C
R
<
0.1
CR < 0.1
CR<0.1,则判断矩阵的一致性可以接受。
而除了CI,还有一个RI值(随机一致性指标),在不同的n的取值下RI值也不同。这个值是通过大量随机实验得到的统计规律,数值可以查表获得,将RI表列在表1.2中。
表1.2 RI取值
| n | 1 | 2 | 3 | 4 | 5 | 6 | 7 |
|---|---|---|---|---|---|---|---|
| RI | 0 | 0 | 0.52 | 0.89 | 1.12 | 1.26 | 1.32 |
| n | 8 | 9 | 10 | 11 | 12 | 13 | 14 |
| RI | 1.41 | 1.46 | 1.49 | 1.52 | 1.54 | 1.56 | 1.58 |
得到RI和CI后,计算CI和RI的比值也就是CR。通常来说,当CR值超过0.1时,就可以认为这个矩阵是不合理的,需要被修改、被调整。这里由于没有超过这个阈值,所以可以认为这个比较矩阵通过了一致性检验。
1.2 层次分析法的案例
假设我们有一个简单的案例:选择一台笔记本电脑,考虑的准则包括价格、性能和外观,备选方案为 A、B 和 C 三台电脑。
1. 建立层次结构
目标:选择最优笔记本电脑
准则:
- 价格
- 性能
- 外观
备选方案:
- 笔记本 A
- 笔记本 B
- 笔记本 C
2. 构建判断矩阵
我们对三个准则进行两两比较,假设得到以下判断矩阵:
A 准则 = ( 1 3 1 / 2 1 / 3 1 1 / 4 2 4 1 ) A_{\text{准则}} = \begin{pmatrix} 1 & 3 & 1/2 \\ 1/3 & 1 & 1/4 \\ 2 & 4 & 1 \end{pmatrix} A准则= 11/323141/21/41
3. 计算权重向量
用 Python 代码计算判断矩阵的最大特征值和对应的特征向量:
import numpy as np
from scipy.linalg import eig
# 判断矩阵
A = np.array([
[1, 3, 0.5],
[1/3, 1, 0.25],
[2, 4, 1]
])
# 计算最大特征值和特征向量
eig_vals, eig_vecs = eig(A)
max_eig_val = np.max(eig_vals)
max_eig_vec = eig_vecs[:, np.argmax(eig_vals)].real
# 标准化特征向量
weights = max_eig_vec / np.sum(max_eig_vec)
weights
4. 一致性检验
# 一致性检验
n = A.shape[0]
CI = (max_eig_val - n) / (n - 1)
RI = 0.58 # 对于 n=3 的随机一致性指数
CR = CI / RI
CR
如果 C R < 0.1 CR < 0.1 CR<0.1,则判断矩阵的一致性可以接受。
5. 计算综合权重
对每个准则分别对备选方案进行两两比较,构建判断矩阵并计算权重,然后综合各准则的权重得到每个备选方案的最终得分。假设得到以下判断矩阵:
-
价格:
A 价格 = ( 1 2 1 / 3 1 / 2 1 1 / 5 3 5 1 ) A_{\text{价格}} = \begin{pmatrix} 1 & 2 & 1/3 \\ 1/2 & 1 & 1/5 \\ 3 & 5 & 1 \end{pmatrix} A价格= 11/232151/31/51 -
性能:
A 性能 = ( 1 1 / 2 3 2 1 4 1 / 3 1 / 4 1 ) A_{\text{性能}} = \begin{pmatrix} 1 & 1/2 & 3 \\ 2 & 1 & 4 \\ 1/3 & 1/4 & 1 \end{pmatrix} A性能= 121/31/211/4341 -
外观:
A 外观 = ( 1 4 2 1 / 4 1 1 / 2 1 / 2 2 1 ) A_{\text{外观}} = \begin{pmatrix} 1 & 4 & 2 \\ 1/4 & 1 & 1/2 \\ 1/2 & 2 & 1 \end{pmatrix} A外观= 11/41/241221/21
同样用上述方法计算每个判断矩阵的权重向量,并根据准则的权重计算每个备选方案的综合得分。
# 价格判断矩阵
A_price = np.array([
[1, 2, 1/3],
[1/2, 1, 1/5],
[3, 5, 1]
])
eig_vals_price, eig_vecs_price = eig(A_price)
weights_price = eig_vecs_price[:, np.argmax(eig_vals_price)].real
weights_price /= np.sum(weights_price)
# 性能判断矩阵
A_performance = np.array([
[1, 1/2, 3],
[2, 1, 4],
[1/3, 1/4, 1]
])
eig_vals_performance, eig_vecs_performance = eig(A_performance)
weights_performance = eig_vecs_performance[:, np.argmax(eig_vals_performance)].real
weights_performance /= np.sum(weights_performance)
# 外观判断矩阵
A_appearance = np.array([
[1, 4, 2],
[1/4, 1, 1/2],
[1/2, 2, 1]
])
eig_vals_appearance, eig_vecs_appearance = eig(A_appearance)
weights_appearance = eig_vecs_appearance[:, np.argmax(eig_vals_appearance)].real
weights_appearance /= np.sum(weights_appearance)
# 综合权重
overall_weights = weights[0] * weights_price + weights[1] * weights_performance + weights[2] * weights_appearance
overall_weights
通过综合各准则的权重,最终得到每个备选方案的综合得分,选择得分最高的方案作为最优方案。
1.3 另一种得出综合得分的方法
1.2中显示对准则层进行判断矩阵计算得到准则层的权重,再对方案层分别人工创建不同的判断矩阵,进而求出不同准则对方案的权重,最后通过准测层权重和不同准则对方案的权重计算得分。
假如已经有了笔记本A、B、C在每个准则(价格、性能、外观)下的评分,只需要将这些评分矩阵与准则权重相乘,即可计算出每个笔记本的综合得分。
例子
假设你有以下评分矩阵:
| 价格 | 性能 | 外观 | |
|---|---|---|---|
| 笔记本A | 7 | 9 | 8 |
| 笔记本B | 5 | 8 | 7 |
| 笔记本C | 8 | 6 | 9 |
权重向量为:
价格权重 = 0.4 , 性能权重 = 0.3 , 外观权重 = 0.3 \text{价格权重} = 0.4, \text{性能权重} = 0.3, \text{外观权重} = 0.3 价格权重=0.4,性能权重=0.3,外观权重=0.3
计算步骤
- 构建评分矩阵:
评分矩阵 = ( 7 9 8 5 8 7 8 6 9 ) \text{评分矩阵} = \begin{pmatrix} 7 & 9 & 8 \\ 5 & 8 & 7 \\ 8 & 6 & 9 \end{pmatrix} 评分矩阵= 758986879
- 构建权重向量:
权重向量 = ( 0.4 0.3 0.3 ) \text{权重向量} = \begin{pmatrix} 0.4 \\ 0.3 \\ 0.3 \end{pmatrix} 权重向量= 0.40.30.3
- 计算综合得分:
综合得分 = 评分矩阵 × 权重向量 \text{综合得分} = \text{评分矩阵} \times \text{权重向量} 综合得分=评分矩阵×权重向量
用Python代码计算:
import numpy as np
# 评分矩阵
scores = np.array([
[7, 9, 8],
[5, 8, 7],
[8, 6, 9]
])
# 权重向量
weights = np.array([0.4, 0.3, 0.3])
# 计算综合得分
overall_scores = scores.dot(weights)
overall_scores
这个代码计算得出综合得分:
笔记本A
=
7
×
0.4
+
9
×
0.3
+
8
×
0.3
=
7.7
\text{笔记本A} = 7 \times 0.4 + 9 \times 0.3 + 8 \times 0.3 = 7.7
笔记本A=7×0.4+9×0.3+8×0.3=7.7
笔记本B
=
5
×
0.4
+
8
×
0.3
+
7
×
0.3
=
6.6
\text{笔记本B} = 5 \times 0.4 + 8 \times 0.3 + 7 \times 0.3 = 6.6
笔记本B=5×0.4+8×0.3+7×0.3=6.6
笔记本C
=
8
×
0.4
+
6
×
0.3
+
9
×
0.3
=
7.5
\text{笔记本C} = 8 \times 0.4 + 6 \times 0.3 + 9 \times 0.3 = 7.5
笔记本C=8×0.4+6×0.3+9×0.3=7.5
所以,笔记本A得分最高,应该选择笔记本A作为最优方案。
完整代码
import numpy as np
# 评分矩阵
scores = np.array([
[7, 9, 8],
[5, 8, 7],
[8, 6, 9]
])
# 权重向量
weights = np.array([0.4, 0.3, 0.3])
# 计算综合得分
overall_scores = scores.dot(weights)
print("综合得分:", overall_scores)
# 找到得分最高的笔记本
best_choice_index = np.argmax(overall_scores)
best_choice = ['笔记本A', '笔记本B', '笔记本C'][best_choice_index]
print("最优方案:", best_choice)
输出:
综合得分: [7.7 6.6 7.5]
最优方案: 笔记本A
这种方法直接利用了评分矩阵和权重向量的矩阵运算,计算出每个备选方案的综合得分,从而选择最优方案。
1.4 层次分析法评价水域情况
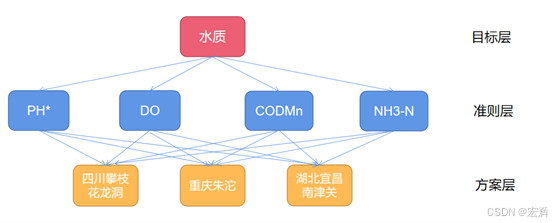
某日从三条河流的基站处抽检水样,得到了水质的四项检测指标如表5.1所示。请根据提供数据对三条河流的水质进行评价。其中,DO代表水中溶解氧含量,越大越好;CODMn表示水中高锰酸盐指数,NH3-N表示氨氮含量,这两项指标越小越好;pH值没有量纲,在6~9区间内较为合适。
水域数据
| 地点名称 | pH* | DO | CODMn | NH3-N |
|---|---|---|---|---|
| 四川攀枝花龙洞 | 7.94 | 9.47 | 1.63 | 0.077 |
| 重庆朱沱 | 8.15 | 9.00 | 1.4 | 0.417 |
| 湖北宜昌南津关 | 8.06 | 8.45 | 2.83 | 0.203 |
首先,我们需要对上面的数据分析:该评价问题一共有三个样本,四个评价指标。不同的评价指标还不太一样,有的越大越好有的越小越好。这里既然他们给出来了评价指标,就不再另外查找文献了。我们构建层次模型图:
接下来的操作就是对目标层到准则层构建一个大小为4的方阵,准则层到方案层构建4个大小为3的方阵。我们先来计算一下这个目标层到准则层,至于准则层到方案层的矩阵都是如法炮制的过程。例如,创建了这么一个矩阵:
| 变量 | pH* | DO | CODMn | NH3-N |
|---|---|---|---|---|
| pH* | 1 | 1/5 | 1/3 | 1 |
| DO | 5 | 1 | 3 | 5 |
| CODMn | 3 | 1/3 | 1 | 3 |
| NH3-N | 1 | 1/5 | 1/3 | 1 |
对这个矩阵做特征值分解的代码如下:
import numpy as np
# 构建矩阵
A=np.array([[1,1/5,1/3,1],
[5,1,3,5],
[3,1/3,1,3],
[1,1/5,1/3,1]])
#获得指标个数
m=len(A)
n=len(A[0])
RI=[0,0,0.58,0.90,1.12,1.24,1.32,1.41,1.45,1.49,1.51]
#求判断矩阵的特征值和特征向量,V为特征值,D为特征向量
V,D=np.linalg.eig(A)
list1=list(V)
#求矩阵的最大特征值
B=np.max(list1)
index=list1.index(B)
C=d[:,index]
很容易地,我们定位到了最大的特征值与特征向量。进而我们计算CI和CR:
CI=(B-n)/(n-1)
CR=CI/RI[n]
if CR<0.10:
print("CI=",CI)
print("CR=",CR)
print("对比矩阵A通过一致性检验,各向量权重向量Q为:")
C_sum=np.sum(C)
Q=C/C_sum
print(Q)
else:
print("对比矩阵A未通过一致性检验,需对对比矩阵A重新构造")
结果输出如下:
将一个成对比较矩阵的AHP过程封装为函数,完整函数如下。
Q:这里分解出来的权重向量为什么是个复数?
注意,python进行矩阵分解的时候是在复数域内进行分解,所得到的向量也是复数向量。虚部为0的情况下想要单独分析实部,通过Q.real即可达成取实部的效果。
4个权重向量的排布
| 地点名称 | pH* | DO | CODMn | NH3-N | 得分 |
|---|---|---|---|---|---|
| 0.0955 | 0.5596 | 0.2495 | 0.0955 | ||
| 四川攀枝花龙洞 | 0.4166 | 0.5396 | 0.2970 | 0.6370 | 0.4767 |
| 重庆朱沱 | 0.3275 | 0.2970 | 0.5396 | 0.1047 | 0.3421 |
| 湖北宜昌南津关 | 0.2599 | 0.1634 | 0.1634 | 0.2583 | 0.1817 |
将准则层到方案层得到的7个成对比较矩阵对应的权重向量排列为一个矩阵,矩阵的每一行表示对应的方案,矩阵的每一列代表评价准则。将这一方案权重矩阵与目标层到准则层的权重向量进行数量积,得到的分数就是最终的评分。最终得到的一个结论是:在评价过程中水中溶解氧含量与钴金属含量占评价体系比重最大,而四川攀枝花龙洞的水质虽然含钴元素比另外两个更高,但由于溶解氧更多,NH3-N的含量更小,水体不显富营养化。就整体而言,四川攀枝花龙洞得分高于重庆朱沱和湖北宜昌南津关。
完整代码如下:
def AHP(A):
m=len(A) #获取指标个数
n=len(A[0])
RI=[0, 0, 0.58, 0.90, 1.12, 1.24, 1.32, 1.41, 1.45, 1.49, 1.51]
R= np.linalg.matrix_rank(A) #求判断矩阵的秩
V,D=np.linalg.eig(A) #求判断矩阵的特征值和特征向量,V特征值,D特征向量;
list1 = list(V)
B= np.max(list1) #最大特征值
index = list1.index(B)
C = D[:, index] #对应特征向量
CI=(B-n)/(n-1) #计算一致性检验指标CI
CR=CI/RI[n]
if CR<0.10:
print("CI=", CI.real)
print("CR=", CR.real)
print('对比矩阵A通过一致性检验,各向量权重向量Q为:')
sum=np.sum(C)
Q=C/sum #特征向量标准化
print(Q.real) # 输出权重向量
return Q.real
else:
print("对比矩阵A未通过一致性检验,需对对比矩阵A重新构造")
return 0
1.5 层次分析法评价植物入侵能力
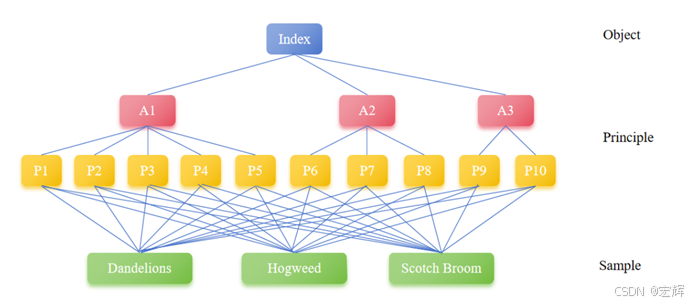
现在想要比较三种草类植物(Dandelions, Hogweed, Scotch Broom)是否在美国构成物种入侵。从A1:生态因素、A2:有益因素、A3:入侵因素三个角度考虑。A1包括五个二级指标:P1:生长速度、P2:竞争能力、P3:生态位占用、P4:生态系统适应性、P5:扩散能力,A2包括三个二级指标:P6:食用价值、P7:药用价值、P8:经济价值,A3包括两个二级指标:P9:扩散历史、P10:入侵地区。请通过层次分析法对三种植物的入侵能力进行综合评价。
这个问题的难点在于,三个一级指标A下面又设置了十个二级指标P。我们首先把层级结构图画出来:
接下来我们分析需要构建的矩阵数量。首先,目标层到一级指标层有一个33的矩阵;A1到下属的五个二级指标有一个55的矩阵,A2就有一个33的矩阵,A3有一个22的矩阵。十个二级指标对应三个比较对象,也就出现了10个3*3的矩阵。通过调用前面的AHP函数就可以构造层级分析表。
#目标层到第一准则层
A0=np.array([[1,3,5],
[1/3,1,3],
[1/5,1/3,1]])
print('目标到第一准则层')
v0=AHP(A0)
#第一准则层到第二准则层
A11 = np.array([[1,5,3,4,2],
[1/5,1,1/2,1,1/3],
[1/3,2,1,2,1/2],
[1/4,1,1/2,1,1/3],
[1/2,3,2,3,1]])
A21 = np.array([[1,3,4],
[1/3,1,2],
[1/4,1/2,1]])
A31 = np.array([[1,3],
[1/3,1]])
print('生态因素')
v11=AHP(A11)
print('有益因素')
v21=AHP(A21)
print('入侵因素')
v31=AHP(A31)
这几个矩阵都是可以通过检验的。剩下十个矩阵就可以如法炮制。最终权重列表如下:
| 顶层设计 | 一级变量 | 顶层权重 | 二级变量 | 二级权重 | 最终权重 |
|---|---|---|---|---|---|
| 评价体系 | 有益因素 | 0.258 | 食用价值 | 0.625 | 0.16125 |
| 评价体系 | 有益因素 | 0.258 | 药用价值 | 0.238 | 0.061404 |
| 评价体系 | 有益因素 | 0.258 | 经济价值 | 0.136 | 0.035088 |
| 评价体系 | 生态因素 | 0.637 | 生长速度 | 0.427 | 0.271999 |
| 评价体系 | 生态因素 | 0.637 | 竞争能力 | 0.082 | 0.052234 |
| 评价体系 | 生态因素 | 0.637 | 生态位占用 | 0.151 | 0.096187 |
| 评价体系 | 生态因素 | 0.637 | 生态系统适应性 | 0.087 | 0.055419 |
| 评价体系 | 生态因素 | 0.637 | 扩散能力 | 0.254 | 0.161798 |
| 评价体系 | 入侵因素 | 0.105 | 扩散历史 | 0.75 | 0.07875 |
| 评价体系 | 入侵因素 | 0.105 | 入侵地区 | 0.25 | 0.02625 |
这样就得到了十个二级指标的最终权重。接下来只需要求解三个样本在每个二级指标上的归一化得分就可以计算出最终评分系数了。这里可能有人会问,n=2的时候RI=0,它能作为分母吗?事实上,当n=2的时候,无论成对比较矩阵长什么样,它最大的特征值都会等于2(有兴趣的同学可以证明一下,不难),CI也就等于0。在CI和RI都为0的时候,我们定义n=2下的成对比较矩阵都能通过一致性检验。最后得到三种植物的分数分别为Dandelions=0.310, Hogweed=0.283, Scotch Broom=0.406。显然,第三种的入侵系数是最高的。
2. 熵权分析法
熵权分析法是一种客观赋权方法,用于确定指标权重,广泛应用于多指标综合评价中。该方法基于信息熵的概念,通过各指标的数据分布来确定权重,避免了主观因素的影响。
2.1 熵权分析法的原理
熵权法的基本原理包括以下几个步骤:
- 数据标准化:对不同量纲的数据进行标准化处理,使其转化为无量纲数据。
- 计算比重:计算每个样本在各指标上的比重。
- 计算熵值:利用信息熵的公式计算各指标的熵值。
- 计算权重:根据熵值计算各指标的权重。
数据标准化
在【数学建模】 数据处理与拟合模型已经详细列举了两种数据标准化方法,在此不再赘述:
- 最小-最大规范化:将数据缩放到一个固定范围(通常是0到1)。
- Z-Score规范化:将数据转换为均值为0、标准差为1的标准正态分布。
假设有 m m m 个样本和 n n n 个指标,原始数据矩阵为 X = ( x i j ) X = (x_{ij}) X=(xij),其中 i i i 表示样本, j j j 表示指标。标准化后得到无量纲矩阵 Y = ( y i j ) Y = (y_{ij}) Y=(yij)。
y i j = x i j − min ( x j ) max ( x j ) − min ( x j ) y_{ij} = \frac{x_{ij} - \min(x_j)}{\max(x_j) - \min(x_j)} yij=max(xj)−min(xj)xij−min(xj)
计算比重
计算每个样本在各指标上的比重 p i j p_{ij} pij:
p i j = y i j ∑ i = 1 m y i j p_{ij} = \frac{y_{ij}}{\sum_{i=1}^m y_{ij}} pij=∑i=1myijyij
计算熵值
利用信息熵公式计算各指标的熵值 e j e_j ej:
e j = − k ∑ i = 1 m p i j ln ( p i j ) e_j = -k \sum_{i=1}^m p_{ij} \ln(p_{ij}) ej=−ki=1∑mpijln(pij)
其中,常数 k = 1 ln ( m ) k = \frac{1}{\ln(m)} k=ln(m)1。
计算权重
根据熵值计算各指标的权重 w j w_j wj:
w j = 1 − e j ∑ j = 1 n ( 1 − e j ) w_j = \frac{1 - e_j}{\sum_{j=1}^n (1 - e_j)} wj=∑j=1n(1−ej)1−ej
2.2 熵权分析法的案例
假设我们有一个简单的案例:选择最优城市,考虑的指标包括经济、环境和教育,样本为城市A、B和C。
1. 原始数据矩阵
| 经济 | 环境 | 教育 | |
|---|---|---|---|
| 城市A | 70 | 80 | 90 |
| 城市B | 60 | 85 | 85 |
| 城市C | 80 | 75 | 80 |
2. 数据标准化
计算标准化后的数据矩阵:
Y = ( 0.5 0.714 1 0 1 0.714 1 0.429 0.429 ) Y = \begin{pmatrix} 0.5 & 0.714 & 1 \\ 0 & 1 & 0.714 \\ 1 & 0.429 & 0.429 \end{pmatrix} Y= 0.5010.71410.42910.7140.429
3. 计算比重
计算每个样本在各指标上的比重 p i j p_{ij} pij:
P = ( 0.333 0.343 0.385 0 0.480 0.275 0.667 0.206 0.165 ) P = \begin{pmatrix} 0.333 & 0.343 & 0.385 \\ 0 & 0.480 & 0.275 \\ 0.667 & 0.206 & 0.165 \end{pmatrix} P= 0.33300.6670.3430.4800.2060.3850.2750.165
4. 计算熵值
计算各指标的熵值 e j e_j ej:
e j = ( 0.562 0.623 0.627 ) e_j = \begin{pmatrix} 0.562 \\ 0.623 \\ 0.627 \end{pmatrix} ej= 0.5620.6230.627
5. 计算权重
根据熵值计算各指标的权重 w j w_j wj:
w j = 1 − e j ∑ j = 1 n ( 1 − e j ) w_j = \frac{1 - e_j}{\sum_{j=1}^n (1 - e_j)} wj=∑j=1n(1−ej)1−ej
用Python代码计算:
import numpy as np
# 原始数据矩阵
X = np.array([
[70, 80, 90],
[60, 85, 85],
[80, 75, 80]
])
# 数据标准化
X_min = X.min(axis=0)
X_max = X.max(axis=0)
Y = (X - X_min) / (X_max - X_min)
# 计算比重
P = Y / Y.sum(axis=0)
# 计算熵值
k = 1.0 / np.log(len(X))
E = -k * (P * np.log(P + 1e-9)).sum(axis=0) # 加1e-9防止log(0)
# 计算权重
W = (1 - E) / (1 - E).sum()
print("标准化后的数据矩阵:\n", Y)
print("比重矩阵:\n", P)
print("熵值:\n", E)
print("权重:\n", W)
计算结果:
标准化后的数据矩阵:
[[0.5 0.71428571 1. ]
[0. 1. 0.71428571]
[1. 0.42857143 0.42857143]]
比重矩阵:
[[0.33333333 0.34328358 0.38461538]
[0. 0.48076923 0.27536232]
[0.66666667 0.20594752 0.34002215]]
熵值:
[0.56233514 0.62343479 0.62748966]
权重:
[0.36345654 0.31100784 0.32553562]
6. 计算综合得分
用计算得到的权重乘以标准化后的数据矩阵,得到每个城市的综合得分:
# 计算综合得分
scores = Y.dot(W)
print("综合得分:", scores)
# 找到得分最高的城市
best_city_index = np.argmax(scores)
best_city = ['城市A', '城市B', '城市C'][best_city_index]
print("最优城市:", best_city)
计算结果:
综合得分: [0.82851179 0.80475935 0.65406501]
最优城市: 城市A
通过熵权分析法,城市A得分最高,因此选择城市A作为最优城市。
3. TOPSIS分析法
TOPSIS(Technique for Order Preference by Similarity to an Ideal Solution)分析法是一种多指标决策分析方法,其基本思想是通过比较各备选方案与理想解和负理想解的距离,来评价和排序各方案的优劣。
3.1 一般的TOPSIS分析法
TOPSIS分析法的基本步骤如下:
-
构建决策矩阵:假设有 m m m 个备选方案和 n n n 个评价指标,构建决策矩阵 X = ( x i j ) X = (x_{ij}) X=(xij),其中 x i j x_{ij} xij 表示第 i i i 个方案在第 j j j 个指标上的值。
-
标准化决策矩阵:为了消除不同指标的量纲影响,将决策矩阵标准化。标准化方法通常是向量归一化:
r i j = x i j ∑ i = 1 m x i j 2 r_{ij} = \frac{x_{ij}}{\sqrt{\sum_{i=1}^m x_{ij}^2}} rij=∑i=1mxij2xij
- 构建加权标准化决策矩阵:根据各指标的权重 w j w_j wj,构建加权标准化决策矩阵:
v i j = w j ⋅ r i j v_{ij} = w_j \cdot r_{ij} vij=wj⋅rij
- 确定正理想解和负理想解:正理想解 A + A^+ A+ 和负理想解 A − A^- A− 分别是各指标的最大值和最小值:
A
+
=
{
v
1
+
,
v
2
+
,
…
,
v
n
+
}
A^+ = \{ v_1^+, v_2^+, \ldots, v_n^+ \}
A+={v1+,v2+,…,vn+}
A
−
=
{
v
1
−
,
v
2
−
,
…
,
v
n
−
}
A^- = \{ v_1^-, v_2^-, \ldots, v_n^- \}
A−={v1−,v2−,…,vn−}
其中,对于效益型指标(值越大越好):
v j + = max i v i j , v j − = min i v i j v_j^+ = \max_i v_{ij}, \quad v_j^- = \min_i v_{ij} vj+=imaxvij,vj−=iminvij
对于成本型指标(值越小越好):
v j + = min i v i j , v j − = max i v i j v_j^+ = \min_i v_{ij}, \quad v_j^- = \max_i v_{ij} vj+=iminvij,vj−=imaxvij
- 计算各备选方案与正负理想解的距离:
正理想解距离:
D i + = ∑ j = 1 n ( v i j − v j + ) 2 D_i^+ = \sqrt{\sum_{j=1}^n (v_{ij} - v_j^+)^2} Di+=j=1∑n(vij−vj+)2
负理想解距离:
D i − = ∑ j = 1 n ( v i j − v j − ) 2 D_i^- = \sqrt{\sum_{j=1}^n (v_{ij} - v_j^-)^2} Di−=j=1∑n(vij−vj−)2
- 计算相对接近度:相对接近度 C i ∗ C_i^* Ci∗ 反映了各方案与理想解的接近程度:
C i ∗ = D i − D i + + D i − C_i^* = \frac{D_i^-}{D_i^+ + D_i^-} Ci∗=Di++Di−Di−
- 根据相对接近度排序:根据 C i ∗ C_i^* Ci∗ 对各方案进行排序,值越大,方案越优。
3.2 改进的TOPSIS分析法
改进的TOPSIS分析法在一般TOPSIS分析法的基础上,针对其不足进行改进,常见的改进方法包括:
- 引入熵权法确定权重:在加权标准化决策矩阵构建中,引入熵权法来客观确定各指标的权重,以减少主观因素的影响。
- 考虑模糊性:将模糊集合理论引入TOPSIS,以处理评价过程中存在的不确定性和模糊性,形成模糊TOPSIS。
- 结合灰色系统理论:将灰色系统理论与TOPSIS结合,利用灰色关联分析来确定各指标与理想解的关系,提高评价结果的可靠性。
- 动态TOPSIS:在多时间点的数据评价中,考虑时间维度的影响,形成动态TOPSIS分析法,以便更准确地反映备选方案的优劣。
3.3 TOPSIS分析法的案例1
假设我们有三个城市(A、B、C),需要从经济、环境和教育三个指标来评价它们的综合发展水平。
1. 构建决策矩阵
| 经济 | 环境 | 教育 | |
|---|---|---|---|
| 城市A | 70 | 80 | 90 |
| 城市B | 60 | 85 | 85 |
| 城市C | 80 | 75 | 80 |
2. 标准化决策矩阵
R = ( 70 7 0 2 + 6 0 2 + 8 0 2 80 8 0 2 + 8 5 2 + 7 5 2 90 9 0 2 + 8 5 2 + 8 0 2 60 7 0 2 + 6 0 2 + 8 0 2 85 8 0 2 + 8 5 2 + 7 5 2 85 9 0 2 + 8 5 2 + 8 0 2 80 7 0 2 + 6 0 2 + 8 0 2 75 8 0 2 + 8 5 2 + 7 5 2 80 9 0 2 + 8 5 2 + 8 0 2 ) R = \begin{pmatrix} \frac{70}{\sqrt{70^2 + 60^2 + 80^2}} & \frac{80}{\sqrt{80^2 + 85^2 + 75^2}} & \frac{90}{\sqrt{90^2 + 85^2 + 80^2}} \\ \frac{60}{\sqrt{70^2 + 60^2 + 80^2}} & \frac{85}{\sqrt{80^2 + 85^2 + 75^2}} & \frac{85}{\sqrt{90^2 + 85^2 + 80^2}} \\ \frac{80}{\sqrt{70^2 + 60^2 + 80^2}} & \frac{75}{\sqrt{80^2 + 85^2 + 75^2}} & \frac{80}{\sqrt{90^2 + 85^2 + 80^2}} \end{pmatrix} R= 702+602+80270702+602+80260702+602+80280802+852+75280802+852+75285802+852+75275902+852+80290902+852+80285902+852+80280
计算标准化矩阵:
R = ( 0.588 0.606 0.646 0.504 0.644 0.609 0.672 0.568 0.574 ) R = \begin{pmatrix} 0.588 & 0.606 & 0.646 \\ 0.504 & 0.644 & 0.609 \\ 0.672 & 0.568 & 0.574 \end{pmatrix} R= 0.5880.5040.6720.6060.6440.5680.6460.6090.574
3. 构建加权标准化决策矩阵
假设各指标权重分别为 w = [ 0.4 , 0.3 , 0.3 ] w = [0.4, 0.3, 0.3] w=[0.4,0.3,0.3],则加权标准化矩阵为:
V = ( 0.4 ⋅ 0.588 0.3 ⋅ 0.606 0.3 ⋅ 0.646 0.4 ⋅ 0.504 0.3 ⋅ 0.644 0.3 ⋅ 0.609 0.4 ⋅ 0.672 0.3 ⋅ 0.568 0.3 ⋅ 0.574 ) V = \begin{pmatrix} 0.4 \cdot 0.588 & 0.3 \cdot 0.606 & 0.3 \cdot 0.646 \\ 0.4 \cdot 0.504 & 0.3 \cdot 0.644 & 0.3 \cdot 0.609 \\ 0.4 \cdot 0.672 & 0.3 \cdot 0.568 & 0.3 \cdot 0.574 \end{pmatrix} V= 0.4⋅0.5880.4⋅0.5040.4⋅0.6720.3⋅0.6060.3⋅0.6440.3⋅0.5680.3⋅0.6460.3⋅0.6090.3⋅0.574
V = ( 0.235 0.182 0.194 0.202 0.193 0.183 0.269 0.170 0.172 ) V = \begin{pmatrix} 0.235 & 0.182 & 0.194 \\ 0.202 & 0.193 & 0.183 \\ 0.269 & 0.170 & 0.172 \end{pmatrix} V= 0.2350.2020.2690.1820.1930.1700.1940.1830.172
4. 确定正理想解和负理想解
正理想解:
A + = { max V 1 j , max V 2 j , max V 3 j } = { 0.269 , 0.193 , 0.194 } A^+ = \{ \max V_{1j}, \max V_{2j}, \max V_{3j} \} = \{ 0.269, 0.193, 0.194 \} A+={maxV1j,maxV2j,maxV3j}={0.269,0.193,0.194}
负理想解:
A − = { min V 1 j , min V 2 j , min V 3 j } = { 0.202 , 0.170 , 0.172 } A^- = \{ \min V_{1j}, \min V_{2j}, \min V_{3j} \} = \{ 0.202, 0.170, 0.172 \} A−={minV1j,minV2j,minV3j}={0.202,0.170,0.172}
5. 计算各方案与正负理想解的距离
正理想解距离:
D i + = ∑ j = 1 n ( v i j − v j + ) 2 D_i^+ = \sqrt{\sum_{j=1}^n (v_{ij} - v_j^+)^2} Di+=j=1∑n(vij−vj+)2
负理想解距离:
D i − = ∑ j = 1 n ( v i j − v j − ) 2 D_i^- = \sqrt{\sum_{j=1}^n (v_{ij} - v_j^-)^2} Di−=j=1∑n(vij−vj−)2
计算得到:
D
A
+
=
(
0.235
−
0.269
)
2
+
(
0.182
−
0.193
)
2
+
(
0.194
−
0.194
)
2
=
0.037
D_A^+ = \sqrt{(0.235-0.269)^2 + (0.182-0.193)^2 + (0.194-0.194)^2} = 0.037
DA+=(0.235−0.269)2+(0.182−0.193)2+(0.194−0.194)2=0.037
D
B
+
=
(
0.202
−
0.269
)
2
+
(
0.193
−
0.193
)
2
+
(
0.183
−
0.194
)
2
=
0.068
D_B^+ = \sqrt{(0.202-0.269)^2 + (0.193-0.193)^2 + (0.183-0.194)^2} = 0.068
DB+=(0.202−0.269)2+(0.193−0.193)2+(0.183−0.194)2=0.068
D
C
+
=
(
0.269
−
0.269
)
2
+
(
0.170
−
0.193
)
2
+
(
0.172
−
0.194
)
2
=
0.031
D_C^+ = \sqrt{(0.269-0.269)^2 + (0.170-0.193)^2 + (0.172-0.194)^2} = 0.031
DC+=(0.269−0.269)2+(0.170−0.193)2+(0.172−0.194)2=0.031
D
A
−
=
(
0.235
−
0.202
)
2
+
(
0.182
−
0.170
)
2
+
(
0.194
−
0.172
)
2
=
0.042
D_A^- = \sqrt{(0.235-0.202)^2 + (0.182-0.170)^2 + (0.194-0.172)^2} = 0.042
DA−=(0.235−0.202)2+(0.182−0.170)2+(0.194−0.172)2=0.042
D
B
−
=
(
0.202
−
0.202
)
2
+
(
0.193
−
0.170
)
2
+
(
0.183
−
0.172
)
2
=
0.024
D_B^- = \sqrt{(0.202-0.202)^2 + (0.193-0.170)^2 + (0.183-0.172)^2} = 0.024
DB−=(0.202−0.202)2+(0.193−0.170)2+(0.183−0.172)2=0.024
D
C
−
=
(
0.269
−
0.202
)
2
+
(
0.170
−
0.170
)
2
+
(
0.172
−
0.172
)
2
=
0.067
D_C^- = \sqrt{(0.269-0.202)^2 + (0.170-0.170)^2 + (0.172-0.172)^2} = 0.067
DC−=(0.269−0.202)2+(0.170−0.170)2+(0.172−0.172)2=0.067
6. 计算相对接近度
C
A
∗
=
D
A
−
D
A
+
+
D
A
−
=
0.042
0.037
+
0.042
=
0.532
C_A^* = \frac{D_A^-}{D_A^+ + D_A^-} = \frac{0.042}{0.037 + 0.042} = 0.532
CA∗=DA++DA−DA−=0.037+0.0420.042=0.532
C
B
∗
=
D
B
−
D
B
+
+
D
B
−
=
0.024
0.068
+
0.024
=
0.261
C_B^* = \frac{D_B^-}{D_B^+ + D_B^-} = \frac{0.024}{0.068 + 0.024} = 0.261
CB∗=DB++DB−DB−=0.068+0.0240.024=0.261
C
C
∗
=
D
C
−
D
C
+
+
D
C
−
=
0.067
0.031
+
0.067
=
0.684
C_C^* = \frac{D_C^-}{D_C^+ + D_C^-} = \frac{0.067}{0.031 + 0.067} = 0.684
CC∗=DC++DC−DC−=0.031+0.0670.067=0.684
7. 排序
根据相对接近度 C i ∗ C_i^* Ci∗ 进行排序:
C C ∗ > C A ∗ > C B ∗ C_C^* > C_A^* > C_B^* CC∗>CA∗>CB∗
因此,城市C综合发展水平最高,其次是城市A,最后是城市B。
3.3 TOPSIS分析法的案例2
1. 构建决策矩阵
| 价格(越低越好) | 性能(越高越好) | 外观(越高越好) | |
|---|---|---|---|
| 笔记本A | 4000 | 80 | 70 |
| 笔记本B | 4500 | 85 | 75 |
| 笔记本C | 4200 | 82 | 78 |
2. 标准化决策矩阵
对于价格(成本型指标):
r
i
j
价格
=
max
i
x
i
j
−
x
i
j
max
i
x
i
j
−
min
i
x
i
j
r_{ij}^{\text{价格}} = \frac{\max_i x_{ij} - x_{ij}}{\max_i x_{ij} - \min_i x_{ij}}
rij价格=maxixij−minixijmaxixij−xij
对于性能和外观(效益型指标):
r
i
j
效益
=
x
i
j
−
min
i
x
i
j
max
i
x
i
j
−
min
i
x
i
j
r_{ij}^{\text{效益}} = \frac{x_{ij} - \min_i x_{ij}}{\max_i x_{ij} - \min_i x_{ij}}
rij效益=maxixij−minixijxij−minixij
计算标准化矩阵:
价格(越低越好):
r
11
=
4500
−
4000
4500
−
4000
=
500
500
=
1
,
r
12
=
4500
−
4500
4500
−
4000
=
0
500
=
0
,
r
13
=
4500
−
4200
4500
−
4000
=
300
500
=
0.6
\begin{aligned} r_{11} &= \frac{4500 - 4000}{4500 - 4000} = \frac{500}{500} = 1, \\ r_{12} &= \frac{4500 - 4500}{4500 - 4000} = \frac{0}{500} = 0, \\ r_{13} &= \frac{4500 - 4200}{4500 - 4000} = \frac{300}{500} = 0.6 \end{aligned}
r11r12r13=4500−40004500−4000=500500=1,=4500−40004500−4500=5000=0,=4500−40004500−4200=500300=0.6
性能(越高越好):
r
21
=
80
−
80
85
−
80
=
0
5
=
0
,
r
22
=
85
−
80
85
−
80
=
5
5
=
1
,
r
23
=
82
−
80
85
−
80
=
2
5
=
0.4
\begin{aligned} r_{21} &= \frac{80 - 80}{85 - 80} = \frac{0}{5} = 0, \\ r_{22} &= \frac{85 - 80}{85 - 80} = \frac{5}{5} = 1, \\ r_{23} &= \frac{82 - 80}{85 - 80} = \frac{2}{5} = 0.4 \end{aligned}
r21r22r23=85−8080−80=50=0,=85−8085−80=55=1,=85−8082−80=52=0.4
外观(越高越好):
r
31
=
70
−
70
78
−
70
=
0
8
=
0
,
r
32
=
75
−
70
78
−
70
=
5
8
=
0.625
,
r
33
=
78
−
70
78
−
70
=
8
8
=
1
\begin{aligned} r_{31} &= \frac{70 - 70}{78 - 70} = \frac{0}{8} = 0, \\ r_{32} &= \frac{75 - 70}{78 - 70} = \frac{5}{8} = 0.625, \\ r_{33} &= \frac{78 - 70}{78 - 70} = \frac{8}{8} = 1 \end{aligned}
r31r32r33=78−7070−70=80=0,=78−7075−70=85=0.625,=78−7078−70=88=1
因此,标准化决策矩阵为:
R
=
(
1
0
0
0
1
0.625
0.6
0.4
1
)
R = \begin{pmatrix} 1 & 0 & 0 \\ 0 & 1 & 0.625 \\ 0.6 & 0.4 & 1 \end{pmatrix}
R=
100.6010.400.6251
3. 构建加权标准化决策矩阵
假设各指标权重分别为
w
=
[
0.4
,
0.3
,
0.3
]
w = [0.4, 0.3, 0.3]
w=[0.4,0.3,0.3],则加权标准化矩阵为:
V
=
R
×
diag
(
w
)
=
(
0.4
⋅
1
0.3
⋅
0
0.3
⋅
0
0.4
⋅
0
0.3
⋅
1
0.3
⋅
0.625
0.4
⋅
0.6
0.3
⋅
0.4
0.3
⋅
1
)
=
(
0.4
0
0
0
0.3
0.1875
0.24
0.12
0.3
)
V = R \times \text{diag}(w) = \begin{pmatrix} 0.4 \cdot 1 & 0.3 \cdot 0 & 0.3 \cdot 0 \\ 0.4 \cdot 0 & 0.3 \cdot 1 & 0.3 \cdot 0.625 \\ 0.4 \cdot 0.6 & 0.3 \cdot 0.4 & 0.3 \cdot 1 \end{pmatrix} = \begin{pmatrix} 0.4 & 0 & 0 \\ 0 & 0.3 & 0.1875 \\ 0.24 & 0.12 & 0.3 \end{pmatrix}
V=R×diag(w)=
0.4⋅10.4⋅00.4⋅0.60.3⋅00.3⋅10.3⋅0.40.3⋅00.3⋅0.6250.3⋅1
=
0.400.2400.30.1200.18750.3
4. 确定正理想解和负理想解
正理想解:
A
+
=
{
max
V
i
j
}
=
{
0.4
,
0.3
,
0.3
}
A^+ = \{ \max V_{ij} \} = \{ 0.4, 0.3, 0.3 \}
A+={maxVij}={0.4,0.3,0.3}
负理想解:
A
−
=
{
min
V
i
j
}
=
{
0
,
0
,
0
}
A^- = \{ \min V_{ij} \} = \{ 0, 0, 0 \}
A−={minVij}={0,0,0}
5. 计算各方案与正负理想解的距离
正理想解距离:
D
i
+
=
∑
j
=
1
n
(
v
i
j
−
v
j
+
)
2
D_i^+ = \sqrt{\sum_{j=1}^n (v_{ij} - v_j^+)^2}
Di+=j=1∑n(vij−vj+)2
负理想解距离:
D
i
−
=
∑
j
=
1
n
(
v
i
j
−
v
j
−
)
2
D_i^- = \sqrt{\sum_{j=1}^n (v_{ij} - v_j^-)^2}
Di−=j=1∑n(vij−vj−)2
计算得到:
笔记本A:
D
A
+
=
(
0.4
−
0.4
)
2
+
(
0
−
0.3
)
2
+
(
0
−
0.3
)
2
=
0
+
0.09
+
0.09
=
0.424
D_A^+ = \sqrt{(0.4-0.4)^2 + (0-0.3)^2 + (0-0.3)^2} = \sqrt{0 + 0.09 + 0.09} = 0.424
DA+=(0.4−0.4)2+(0−0.3)2+(0−0.3)2=0+0.09+0.09=0.424
D
A
−
=
(
0.4
−
0
)
2
+
(
0
−
0
)
2
+
(
0
−
0
)
2
=
0.16
+
0
+
0
=
0.4
D_A^- = \sqrt{(0.4-0)^2 + (0-0)^2 + (0-0)^2} = \sqrt{0.16 + 0 + 0} = 0.4
DA−=(0.4−0)2+(0−0)2+(0−0)2=0.16+0+0=0.4
笔记本B:
D
B
+
=
(
0
−
0.4
)
2
+
(
0.3
−
0.3
)
2
+
(
0.1875
−
0.3
)
2
=
0.16
+
0
+
0.01265625
=
0.406
D_B^+ = \sqrt{(0-0.4)^2 + (0.3-0.3)^2 + (0.1875-0.3)^2} = \sqrt{0.16 + 0 + 0.01265625} = 0.406
DB+=(0−0.4)2+(0.3−0.3)2+(0.1875−0.3)2=0.16+0+0.01265625=0.406
D
B
−
=
(
0
−
0
)
2
+
(
0.3
−
0
)
2
+
(
0.1875
−
0
)
2
=
0
+
0.09
+
0.03515625
=
0.358
D_B^- = \sqrt{(0-0)^2 + (0.3-0)^2 + (0.1875-0)^2} = \sqrt{0 + 0.09 + 0.03515625} = 0.358
DB−=(0−0)2+(0.3−0)2+(0.1875−0)2=0+0.09+0.03515625=0.358
笔记本C:
D
C
+
=
(
0.24
−
0.4
)
2
+
(
0.12
−
0.3
)
2
+
(
0.3
−
0.3
)
2
=
0.0256
+
0.0324
+
0
=
0.254
D_C^+ = \sqrt{(0.24-0.4)^2 + (0.12-0.3)^2 + (0.3-0.3)^2} = \sqrt{0.0256 + 0.0324 + 0} = 0.254
DC+=(0.24−0.4)2+(0.12−0.3)2+(0.3−0.3)2=0.0256+0.0324+0=0.254
D
C
−
=
(
0.24
−
0
)
2
+
(
0.12
−
0
)
2
+
(
0.3
−
0
)
2
=
0.0576
+
0.0144
+
0.09
=
0.371
D_C^- = \sqrt{(0.24-0)^2 + (0.12-0)^2 + (0.3-0)^2} = \sqrt{0.0576 + 0.0144 + 0.09} = 0.371
DC−=(0.24−0)2+(0.12−0)2+(0.3−0)2=0.0576+0.0144+0.09=0.371
6. 计算相对接近度
C
A
∗
=
D
A
−
D
A
+
+
D
A
−
=
0.4
0.424
+
0.4
=
0.485
C_A^* = \frac{D_A^-}{D_A^+ + D_A^-} = \frac{0.4}{0.424 + 0.4} = 0.485
CA∗=DA++DA−DA−=0.424+0.40.4=0.485
C
B
∗
=
D
B
−
D
B
+
+
D
B
−
=
0.358
0.406
+
0.358
=
0.469
C_B^* = \frac{D_B^-}{D_B^+ + D_B^-} = \frac{0.358}{0.406 + 0.358} = 0.469
CB∗=DB++DB−DB−=0.406+0.3580.358=0.469
C
C
∗
=
D
C
−
D
C
+
+
D
C
−
=
0.371
0.254
+
0.371
=
0.593
C_C^* = \frac{D_C^-}{D_C^+ + D_C^-} = \frac{0.371}{0.254 + 0.371} = 0.593
CC∗=DC++DC−DC−=0.254+0.3710.371=0.593
7. 排序
根据相对接近度 C i ∗ C_i^* Ci∗ 进行排序:
C C ∗ > C A ∗ > C B ∗ C_C^* > C_A^* > C_B^* CC∗>CA∗>CB∗
因此,笔记本C综合评价最好,其次是笔记本A,最后是笔记本B。
3.4 TOPSIS分析法总结
TOPSIS分析法提供了一种直观有效的多指标决策方法,通过比较各方案与理想解和负理想解的距离,来评价和排序各方案的优劣。其改进方法如熵权法、模糊TOPSIS、灰色TOPSIS和动态TOPSIS,进一步增强了TOPSIS在不同场景下的适用性和准确性。在实际应用中,选择合适的改进方法和权重确定方法,可以更好地满足具体问题的需求。
4. CRITIC方法
CRITIC(Criteria Importance Through Intercriteria Correlation)权重法是一种基于数据波动性的客观赋权方法。其思想在于两项指标:波动性(对比强度)和冲突性(相关性)。对比强度使用标准差进行表示,如果数据标准差越大,说明波动越大,权重会越高;冲突性使用相关系数进行表示,如果指标之间的相关系数值越大,说明冲突性越小,那么其权重也就越低。权重计算时,对比强度与冲突性指标相乘,并进行归一化处理,即得到最终的权重。CRITIC权重法适用于数据稳定性可视作一种信息,并且分析的指标或因素之间有一定关联关系的数据。
4.1 CRITIC分析法的原理
在数据分析中,我们经常需要评估多个指标的好坏,但这些指标的标准往往不统一。这时,可以使用CRITIC法来统一标准。这种方法的基本原理是综合考虑对比强度和指标的变异程度,从而为每个指标赋予一个客观的权重。这种方法之所以是正确的,是因为它不仅考虑了指标之间的相对重要性,还考虑了指标本身的波动性,使得权重更加客观和准确。
注意:CRITIC方法和熵权法一样,都属于数据驱动的方法类型,需要数据量支持。
假设有一个n个对象m项指标的数表,CRITIC法按照如下操作步骤进行:
-
对指标进行无量纲化和正向化处理:
使用min-max规约进行无量纲化处理。如果指标是越大越好,规约方法为:
x new = x − min ( x ) max ( x ) − min ( x ) x_{\text{new}} = \frac{x - \min(x)}{\max(x) - \min(x)} xnew=max(x)−min(x)x−min(x)
如果指标是越小越好,规约方法为:
x new = max ( x ) − x max ( x ) − min ( x ) x_{\text{new}} = \frac{\max(x) - x}{\max(x) - \min(x)} xnew=max(x)−min(x)max(x)−x -
计算指标变异性:
计算每个指标在所有样本中的标准差 S j S_j Sj。标准差表示指标在样本中的差异波动情况,若标准差越大,则其区分度越明显,信息强度也越高,越应该分配更多权重。 -
计算指标冲突性:
定义为:
R j = ∑ i = 1 m ( 1 − r i j ) R_j = \sum_{i=1}^{m} (1 - r_{ij}) Rj=i=1∑m(1−rij)
其中 r i j r_{ij} rij表示指标 i i i和指标 j j j之间的相关系数。其定义为:
r i j = ∑ k = 1 n ( x i k y j k ) − n x ˉ i y ˉ j ∑ k = 1 n x i k 2 − n x ˉ i 2 ∑ k = 1 n y j k 2 − n y ˉ j 2 r_{ij} = \frac{\sum_{k=1}^{n} (x_{ik} y_{jk}) - n \bar{x}_i \bar{y}_j}{\sqrt{\sum_{k=1}^{n} x_{ik}^2 - n \bar{x}_i^2} \sqrt{\sum_{k=1}^{n} y_{jk}^2 - n \bar{y}_j^2}} rij=∑k=1nxik2−nxˉi2∑k=1nyjk2−nyˉj2∑k=1n(xikyjk)−nxˉiyˉj -
获取信息量:
信息量的定义为指标变异性和冲突性的乘积:
C j = S j ∑ i = 1 m ( 1 − r i j ) C_j = S_j \sum_{i=1}^{m} (1 - r_{ij}) Cj=Sji=1∑m(1−rij) -
归一化得到指标权重:
用权重去乘归一化的数据矩阵可以得到每个对象的评分,并根据评分进行对象的评价、排序。归一化过程为:
w j = C j ∑ i = 1 m C i w_j = \frac{C_j}{\sum_{i=1}^{m} C_i} wj=∑i=1mCiCj
CRITIC方法和熵权法都是用于确定评价指标权重的综合评价方法,并且都是基于数据驱动,通过计算一列数据的信息量来归一化得到权重的。不同的是,CRITIC方法综合考虑了标准差和相关系数来确定权重,而熵权法只考虑了信息熵。CRITIC方法适用于具有明显客观标准的数据,而熵权法更适用于具有主观判断的数据。
4.2 CRITIC分析法的案例
下面通过一个详细案例来说明CRITIC方法的具体应用。
假设我们有三个对象(A, B, C)和三个指标(X1, X2, X3)的数据,如下表所示:
| 对象 | X1 | X2 | X3 |
|---|---|---|---|
| A | 5.0 | 7.0 | 8.0 |
| B | 6.0 | 9.0 | 5.0 |
| C | 8.0 | 6.0 | 7.0 |
-
对指标进行无量纲化和正向化处理:
计算无量纲化后的数据:
对于X1(越大越好):
X 1 A = 5 − 5 8 − 5 = 0.00 X 1 B = 6 − 5 8 − 5 = 0.33 X 1 C = 8 − 5 8 − 5 = 1.00 \begin{align*} X1_A &= \frac{5 - 5}{8 - 5} = 0.00 \\ X1_B &= \frac{6 - 5}{8 - 5} = 0.33 \\ X1_C &= \frac{8 - 5}{8 - 5} = 1.00 \\ \end{align*} X1AX1BX1C=8−55−5=0.00=8−56−5=0.33=8−58−5=1.00对于X2(越大越好):
X 2 A = 7 − 6 9 − 6 = 0.33 X 2 B = 9 − 6 9 − 6 = 1.00 X 2 C = 6 − 6 9 − 6 = 0.00 \begin{align*} X2_A &= \frac{7 - 6}{9 - 6} = 0.33 \\ X2_B &= \frac{9 - 6}{9 - 6} = 1.00 \\ X2_C &= \frac{6 - 6}{9 - 6} = 0.00 \\ \end{align*} X2AX2BX2C=9−67−6=0.33=9−69−6=1.00=9−66−6=0.00对于X3(越大越好):
X 3 A = 8 − 5 8 − 5 = 1.00 X 3 B = 5 − 5 8 − 5 = 0.00 X 3 C = 7 − 5 8 − 5 = 0.67 \begin{align*} X3_A &= \frac{8 - 5}{8 - 5} = 1.00 \\ X3_B &= \frac{5 - 5}{8 - 5} = 0.00 \\ X3_C &= \frac{7 - 5}{8 - 5} = 0.67 \\ \end{align*} X3AX3BX3C=8−58−5=1.00=8−55−5=0.00=8−57−5=0.67无量纲化后的数据表:
对象 X1 X2 X3 A 0.00 0.33 1.00 B 0.33 1.00 0.00 C 1.00 0.00 0.67 -
计算指标变异性:
计算标准差 S j S_j Sj:
S X 1 = ( 0.00 − 0.44 ) 2 + ( 0.33 − 0.44 ) 2 + ( 1.00 − 0.44 ) 2 3 = 0.50 S X 2 = ( 0.33 − 0.44 ) 2 + ( 1.00 − 0.44 ) 2 + ( 0.00 − 0.44 ) 2 3 = 0.47 S X 3 = ( 1.00 − 0.56 ) 2 + ( 0.00 − 0.56 ) 2 + ( 0.67 − 0.56 ) 2 3 = 0.47 \begin{align*} S_{X1} &= \sqrt{\frac{(0.00-0.44)^2 + (0.33-0.44)^2 + (1.00-0.44)^2}{3}} = 0.50 \\ S_{X2} &= \sqrt{\frac{(0.33-0.44)^2 + (1.00-0.44)^2 + (0.00-0.44)^2}{3}} = 0.47 \\ S_{X3} &= \sqrt{\frac{(1.00-0.56)^2 + (0.00-0.56)^2 + (0.67-0.56)^2}{3}} = 0.47 \\ \end{align*} SX1SX2SX3=3(0.00−0.44)2+(0.33−0.44)2+(1.00−0.44)2=0.50=3(0.33−0.44)2+(1.00−0.44)2+(0.00−0.44)2=0.47=3(1.00−0.56)2+(0.00−0.56)2+(0.67−0.56)2=0.47
-
计算指标冲突性:
计算相关系数 r i j r_{ij} rij并计算冲突性 R j R_j Rj:
相关系数矩阵为:
X1 X2 X3 X1 1.00 -0.50 0.87 X2 -0.50 1.00 -0.98 X3 0.87 -0.98 1.00 计算冲突性 R j R_j Rj:
R X 1 = ( 1 − 1.00 ) + ( 1 − ( − 0.50 ) ) + ( 1 − 0.87 ) = 2.63 R X 2 = ( 1 − ( − 0.50 ) ) + ( 1 − 1.00 ) + ( 1 − ( − 0.98 ) ) = 3.48 R X 3 = ( 1 − 0.87 ) + ( 1 − ( − 0.98 ) ) + ( 1 − 1.00 ) = 2.11 \begin{align*} R_{X1} &= (1 - 1.00) + (1 - (-0.50)) + (1 - 0.87) = 2.63 \\ R_{X2} &= (1 - (-0.50)) + (1 - 1.00) + (1 - (-0.98)) = 3.48 \\ R_{X3} &= (1 - 0.87) + (1 - (-0.98)) + (1 - 1.00) = 2.11 \\ \end{align*} RX1RX2RX3=(1−1.00)+(1−(−0.50))+(1−0.87)=2.63=(1−(−0.50))+(1−1.00)+(1−(−0.98))=3.48=(1−0.87)+(1−(−0.98))+(1−1.00)=2.11
-
获取信息量:
计算信息量 C j C_j Cj:
C X 1 = 0.50 × 2.63 = 1.315 C X 2 = 0.47 × 3.48 = 1.636 C X 3 = 0.47 × 2.11 = 0.992 \begin{align*} C_{X1} &= 0.50 \times 2.63 = 1.315 \\ C_{X2} &= 0.47 \times 3.48 = 1.636 \\ C_{X3} &= 0.47 \times 2.11 = 0.992 \\ \end{align*} CX1CX2CX3=0.50×2.63=1.315=0.47×3.48=1.636=0.47×2.11=0.992
-
归一化得到指标权重:
计算归一化后的权重 w j w_j wj:
w X 1 = 1.315 1.315 + 1.636 + 0.992 = 0.296 w X 2 = 1.636 1.315 + 1.636 + 0.992 = 0.368 w X 3 = 0.992 1.315 + 1.636 + 0.992 = 0.223 \begin{align*} w_{X1} &= \frac{1.315}{1.315 + 1.636 + 0.992} = 0.296 \\ w_{X2} &= \frac{1.636}{1.315 + 1.636 + 0.992} = 0.368 \\ w_{X3} &= \frac{0.992}{1.315 + 1.636 + 0.992} = 0.223 \\ \end{align*} wX1wX2wX3=1.315+1.636+0.9921.315=0.296=1.315+1.636+0.9921.636=0.368=1.315+1.636+0.9920.992=0.223
归一化后的权重为:
| 指标 | 权重 |
|---|---|
| X1 | 0.296 |
| X2 | 0.368 |
| X3 | 0.223 |
通过CRITIC方法得出的权重,可以对每个对象进行评分和排序,具体过程如下:
-
计算每个对象的评分:
Score A = 0.00 × 0.296 + 0.33 × 0.368 + 1.00 × 0.223 = 0.362 Score B = 0.33 × 0.296 + 1.00 × 0.368 + 0.00 × 0.223 = 0.464 Score C = 1.00 × 0.296 + 0.00 × 0.368 + 0.67 × 0.223 = 0.445 \begin{align*} \text{Score}_A &= 0.00 \times 0.296 + 0.33 \times 0.368 + 1.00 \times 0.223 = 0.362 \\ \text{Score}_B &= 0.33 \times 0.296 + 1.00 \times 0.368 + 0.00 \times 0.223 = 0.464 \\ \text{Score}_C &= 1.00 \times 0.296 + 0.00 \times 0.368 + 0.67 \times 0.223 = 0.445 \\ \end{align*} ScoreAScoreBScoreC=0.00×0.296+0.33×0.368+1.00×0.223=0.362=0.33×0.296+1.00×0.368+0.00×0.223=0.464=1.00×0.296+0.00×0.368+0.67×0.223=0.445
根据评分,对象的评价和排序结果为:B > C > A。
这样,通过CRITIC方法,我们可以客观地对多个对象进行综合评价和排序。
5. 一些奇奇怪怪的疑问
5.1 为什么熵权法计算权重的公式是 w j = 1 − e j ∑ j = 1 n ( 1 − e j ) w_j = \frac{1 - e_j}{\sum_{j=1}^n (1 - e_j)} wj=∑j=1n(1−ej)1−ej
在熵权分析法中,计算权重的公式
W
=
1
−
E
j
∑
j
=
1
n
(
1
−
E
j
)
W = \frac{1 - E_j}{\sum_{j=1}^n (1 - E_j)}
W=∑j=1n(1−Ej)1−Ej 的核心思想是通过信息熵来反映各指标的重要性。具体来说:
-
信息熵 E j E_j Ej 的含义:
- 信息熵(Entropy)用于衡量信息的不确定性或混乱程度。在多指标评价中,某个指标的信息熵越大,说明该指标的数据分布越均匀、不确定性越高,该指标提供的信息量越小。
- 反之,信息熵越小,说明该指标的数据分布越集中、不确定性越低,该指标提供的信息量越大。
-
1 − E j 1 - E_j 1−Ej 的含义:
- 为了得到各指标的重要性权重,我们需要对信息熵进行转换。通过计算 1 − E j 1 - E_j 1−Ej,我们将高熵值(不重要的指标)转换为低权重,将低熵值(重要的指标)转换为高权重。这样,信息量大的指标(即熵值低的指标)会得到较大的权重,反之则权重较小。
-
归一化处理:
- 由于 1 − E j 1 - E_j 1−Ej 的总和不一定为1,因此需要进行归一化处理。将每个指标的 1 − E j 1 - E_j 1−Ej 除以所有指标的 1 − E j 1 - E_j 1−Ej 之和,即:
W j = 1 − E j ∑ j = 1 n ( 1 − E j ) W_j = \frac{1 - E_j}{\sum_{j=1}^n (1 - E_j)} Wj=∑j=1n(1−Ej)1−Ej
这样可以确保所有权重之和为1,使得权重具有可比性。
通过这种方法,熵权分析法将主观因素最小化,客观地根据数据分布计算各指标的权重。
例子
假设我们有以下熵值:
E = ( 0.562 0.623 0.627 ) E = \begin{pmatrix} 0.562 \\ 0.623 \\ 0.627 \end{pmatrix} E= 0.5620.6230.627
我们需要计算每个指标的权重 W W W。
计算步骤
- 计算 1 − E j 1 - E_j 1−Ej:
1 − E = ( 1 − 0.562 1 − 0.623 1 − 0.627 ) = ( 0.438 0.377 0.373 ) 1 - E = \begin{pmatrix} 1 - 0.562 \\ 1 - 0.623 \\ 1 - 0.627 \end{pmatrix} = \begin{pmatrix} 0.438 \\ 0.377 \\ 0.373 \end{pmatrix} 1−E= 1−0.5621−0.6231−0.627 = 0.4380.3770.373
- 计算 ∑ j = 1 n ( 1 − E j ) \sum_{j=1}^n (1 - E_j) ∑j=1n(1−Ej):
∑ j = 1 n ( 1 − E j ) = 0.438 + 0.377 + 0.373 = 1.188 \sum_{j=1}^n (1 - E_j) = 0.438 + 0.377 + 0.373 = 1.188 j=1∑n(1−Ej)=0.438+0.377+0.373=1.188
- 计算权重 W j W_j Wj:
W j = 1 − E j ∑ j = 1 n ( 1 − E j ) W_j = \frac{1 - E_j}{\sum_{j=1}^n (1 - E_j)} Wj=∑j=1n(1−Ej)1−Ej
计算得到:
W = ( 0.438 1.188 0.377 1.188 0.373 1.188 ) = ( 0.369 0.317 0.314 ) W = \begin{pmatrix} \frac{0.438}{1.188} \\\\ \frac{0.377}{1.188} \\\\ \frac{0.373}{1.188} \end{pmatrix} = \begin{pmatrix} 0.369 \\ 0.317 \\ 0.314 \end{pmatrix} W= 1.1880.4381.1880.3771.1880.373 = 0.3690.3170.314
用Python代码计算:
import numpy as np
# 熵值
E = np.array([0.562, 0.623, 0.627])
# 计算1 - E
one_minus_E = 1 - E
# 计算权重
W = one_minus_E / one_minus_E.sum()
print("权重:", W)
计算结果:
权重: [0.36936292 0.31709264 0.31354444]
因此,熵权分析法通过这种方式客观地确定各指标的权重,保证了评价结果的公正性和科学性。
5.2 熵权法的应用场景和局限性
熵权法的应用场景
- 多指标综合评价:熵权法广泛用于需要综合多个指标进行评价的场景,如城市综合评价、项目评估、环境质量评价等。
- 数据客观赋权:适用于数据较为完备且需要通过客观方法确定各指标权重的情况,避免人为主观因素的影响。
- 指标分布均匀:特别适用于各指标的数据分布较为均匀,且希望通过客观方法评估各指标相对重要性的场景。
- 自动化评价系统:在需要构建自动化、多维度评价系统的应用中,熵权法提供了一种基于数据本身特征的赋权方法。
熵权法的局限性
- 指标重要性与熵值不一致:熵权法假设熵值高的指标提供的信息量少,但在实际中,某些熵值高的指标可能确实非常重要,单纯依赖熵值会低估其重要性。
- 数据质量依赖性:熵权法依赖于输入数据的质量,如果数据存在偏差或异常,可能会影响最终结果。
- 忽略主观因素:完全依赖客观数据进行权重计算,可能忽略了一些需要主观判断的重要因素。
- 不适合少量数据:在样本数量较少的情况下,熵值计算的准确性可能受到影响,从而影响权重的可靠性。
- 数据分布的敏感性:对于数据分布极端不均匀的指标,熵权法可能会赋予过高的权重,需要结合其他方法进行平衡。
5.3 根据相对接近度排序:根据 C i ∗ C_i^* Ci∗ 对各方案进行排序,值越大,方案越优。为什么不用 D i + D i + + D i − \frac{D_i^+}{D_i^+ + D_i^-} Di++Di−Di+来进行比较?
在TOPSIS(Technique for Order of Preference by Similarity to Ideal Solution)方法中,使用相对接近度 C i ∗ C_i^* Ci∗ 来排序备选方案时,采用公式:
C i ∗ = D i − D i + + D i − C_i^* = \frac{D_i^-}{D_i^+ + D_i^-} Ci∗=Di++Di−Di−
这个公式的设计是基于以下原因:
-
概念一致性:TOPSIS方法的核心思想是选择与正理想解(最优解)距离最小、与负理想解(最差解)距离最大的方案。通过比较 D i − D_i^- Di− 和 D i + D_i^+ Di+ 可以更直观地衡量一个方案的优劣。相对接近度 C i ∗ C_i^* Ci∗ 反映了一个方案与正理想解的接近程度,同时也考虑了与负理想解的距离。
-
范围合理性:相对接近度 C i ∗ C_i^* Ci∗ 的值在0到1之间,当 C i ∗ C_i^* Ci∗ 值越接近1时,表示该方案越优。因此,便于解释和比较。
-
平衡评价:该公式综合考虑了方案与正理想解和负理想解的距离。既考虑了接近最优解(通过 D i − D_i^- Di−),也考虑了远离最差解(通过 D i + D_i^+ Di+)。
如果使用 D i + D i + + D i − \frac{D_i^+}{D_i^+ + D_i^-} Di++Di−Di+ 进行比较,公式虽然看似对称,但实际效果与使用 D i − D i + + D i − \frac{D_i^-}{D_i^+ + D_i^-} Di++Di−Di− 是一样的。我们可以通过变换公式来证明这一点:
假设:
C i ∗ = D i − D i + + D i − C_i^* = \frac{D_i^-}{D_i^+ + D_i^-} Ci∗=Di++Di−Di−
那么:
1 − C i ∗ = D i + D i + + D i − 1 - C_i^* = \frac{D_i^+}{D_i^+ + D_i^-} 1−Ci∗=Di++Di−Di+
由此可以看出,使用
D
i
+
D
i
+
+
D
i
−
\frac{D_i^+}{D_i^+ + D_i^-}
Di++Di−Di+ 实际上是
D
i
−
D
i
+
+
D
i
−
\frac{D_i^-}{D_i^+ + D_i^-}
Di++Di−Di− 的补数,两个公式表达的是相同的排名结果,只是排序顺序相反。
在TOPSIS方法中,使用
D
i
−
D
i
+
+
D
i
−
\frac{D_i^-}{D_i^+ + D_i^-}
Di++Di−Di− 来计算相对接近度有助于直观理解方案的优劣。该公式确保了相对接近度的值在0到1之间,值越大表示方案越优。同时,该公式综合考虑了正理想解和负理想解的距离,使得评价更加平衡和合理。
5.4 什么是皮尔逊相关系数,有什么应用
皮尔逊相关系数(Pearson correlation coefficient)是用来衡量两个变量之间线性相关程度的统计指标。其取值范围在-1到1之间:
- 1 表示完全正相关,即一个变量增加,另一个变量也增加,且关系完全线性。
- -1 表示完全负相关,即一个变量增加,另一个变量减少,且关系完全线性。
- 0 表示无相关,即两个变量之间没有线性关系。
皮尔逊相关系数公式为:
r
x
y
=
∑
i
=
1
n
(
x
i
−
x
ˉ
)
(
y
i
−
y
ˉ
)
∑
i
=
1
n
(
x
i
−
x
ˉ
)
2
∑
i
=
1
n
(
y
i
−
y
ˉ
)
2
r_{xy} = \frac{\sum_{i=1}^n (x_i - \bar{x})(y_i - \bar{y})}{\sqrt{\sum_{i=1}^n (x_i - \bar{x})^2 \sum_{i=1}^n (y_i - \bar{y})^2}}
rxy=∑i=1n(xi−xˉ)2∑i=1n(yi−yˉ)2∑i=1n(xi−xˉ)(yi−yˉ)
其中,
x
i
x_i
xi和
y
i
y_i
yi分别是两个变量的观测值,
x
ˉ
\bar{x}
xˉ和
y
ˉ
\bar{y}
yˉ分别是两个变量的平均值。
皮尔逊相关系数的应用
皮尔逊相关系数在许多领域都有广泛的应用,以下是一些常见的应用场景:
-
经济学与金融学:
- 分析股票收益率之间的相关性,以构建投资组合和分散风险。
- 研究不同经济指标(如通货膨胀率和失业率)之间的关系。
-
心理学与社会科学:
- 评估不同心理测验分数之间的相关性,研究人类行为和心理特征之间的关系。
- 分析社会调查数据中不同变量(如收入和幸福感)之间的相关性。
-
医学与生物学:
- 研究不同生物指标(如血压和胆固醇水平)之间的关系,以探索健康风险因素。
- 分析基因表达数据,研究不同基因之间的相互关系。
-
市场研究:
- 分析消费者行为数据,研究不同产品特性(如价格和销量)之间的关系。
- 评估市场营销活动效果,研究广告支出和销售额之间的相关性。
-
工程与物理科学:
- 分析实验数据,研究不同物理量(如温度和压力)之间的关系。
- 优化工程设计,研究不同设计参数(如材料强度和重量)之间的相关性。
皮尔逊相关系数是一个强大的统计工具,可以帮助研究人员和分析师理解和量化变量之间的线性关系,提供有价值的洞察力和决策支持。
5.5 为什么计算指标冲突性:定义为: R j = ∑ i = 1 m ( 1 − r i j ) R_j = \sum_{i=1}^{m} (1 - r_{ij}) Rj=∑i=1m(1−rij)
在CRITIC方法中,计算指标冲突性是为了衡量一个指标与其他指标之间的独立性或独特性。具体定义为:
R
j
=
∑
i
=
1
m
(
1
−
r
i
j
)
R_j = \sum_{i=1}^{m} (1 - r_{ij})
Rj=i=1∑m(1−rij)
这里, R j R_j Rj表示第 j j j个指标的冲突性, r i j r_{ij} rij表示第 i i i个指标和第 j j j个指标之间的皮尔逊相关系数, m m m是指标的总数。
理由和解释
-
相关性反映重复信息:
- 如果两个指标之间的相关性( r i j r_{ij} rij)很高,意味着它们提供了相似的信息。换句话说,一个指标的变化可以通过另一个指标的变化来解释。
- 高度相关的指标对整体信息贡献较少,因为它们的重复信息较多。
-
降低高相关性指标的权重:
- 通过计算 1 − r i j 1 - r_{ij} 1−rij,我们获得的是一个"冲突度"。如果两个指标高度正相关( r i j r_{ij} rij接近1),那么 1 − r i j 1 - r_{ij} 1−rij就接近0,表示这两个指标之间的信息冲突性小。
- 如果两个指标低相关或负相关( r i j r_{ij} rij接近0或负数),那么 1 − r i j 1 - r_{ij} 1−rij就接近1或更大,表示这两个指标之间的信息冲突性大。
-
综合所有冲突度:
- R j = ∑ i = 1 m ( 1 − r i j ) R_j = \sum_{i=1}^{m} (1 - r_{ij}) Rj=∑i=1m(1−rij)表示第 j j j个指标与所有其他指标的冲突性的总和。这个总和越大,说明第 j j j个指标与其他指标的相关性越低,信息越独特,越值得赋予更多权重。
- 通过这种方式,CRITIC方法能够确保每个指标的权重不仅考虑其波动性(标准差),还考虑其与其他指标的相关性,从而提高权重分配的客观性和合理性。
数学直观解释
假设有三个指标 X 1 , X 2 , X 3 X1, X2, X3 X1,X2,X3,计算它们之间的相关系数矩阵:
| X1 | X2 | X3 | |
|---|---|---|---|
| X1 | 1.00 | 0.50 | 0.30 |
| X2 | 0.50 | 1.00 | 0.70 |
| X3 | 0.30 | 0.70 | 1.00 |
计算每个指标的冲突性:
- 对于
X
1
X1
X1:
R X 1 = ( 1 − 1.00 ) + ( 1 − 0.50 ) + ( 1 − 0.30 ) = 0 + 0.50 + 0.70 = 1.20 R_{X1} = (1 - 1.00) + (1 - 0.50) + (1 - 0.30) = 0 + 0.50 + 0.70 = 1.20 RX1=(1−1.00)+(1−0.50)+(1−0.30)=0+0.50+0.70=1.20 - 对于
X
2
X2
X2:
R X 2 = ( 1 − 0.50 ) + ( 1 − 1.00 ) + ( 1 − 0.70 ) = 0.50 + 0 + 0.30 = 0.80 R_{X2} = (1 - 0.50) + (1 - 1.00) + (1 - 0.70) = 0.50 + 0 + 0.30 = 0.80 RX2=(1−0.50)+(1−1.00)+(1−0.70)=0.50+0+0.30=0.80 - 对于
X
3
X3
X3:
R X 3 = ( 1 − 0.30 ) + ( 1 − 0.70 ) + ( 1 − 1.00 ) = 0.70 + 0.30 + 0 = 1.00 R_{X3} = (1 - 0.30) + (1 - 0.70) + (1 - 1.00) = 0.70 + 0.30 + 0 = 1.00 RX3=(1−0.30)+(1−0.70)+(1−1.00)=0.70+0.30+0=1.00
从冲突性 R j R_j Rj的值可以看出, X 1 X1 X1的冲突性最大, X 2 X2 X2的冲突性最小。这意味着 X 1 X1 X1包含最多独特信息,而 X 2 X2 X2包含最少独特信息。
通过这种方法,我们能够根据每个指标的独特信息量来分配权重,确保每个指标的贡献是基于其独特性和波动性,而不是仅仅基于其单独的波动性(标准差)。这使得CRITIC方法在权重分配时更加合理和全面。