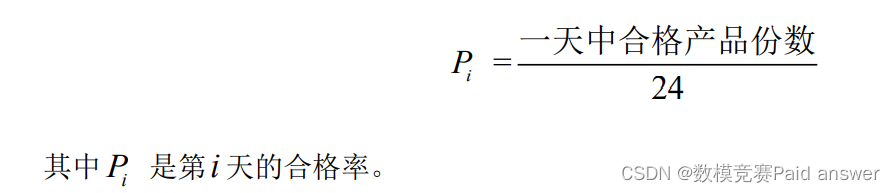2022年五一杯数学建模B题
矿石加工质量控制问题
多篇论文给您参考
原题再现:
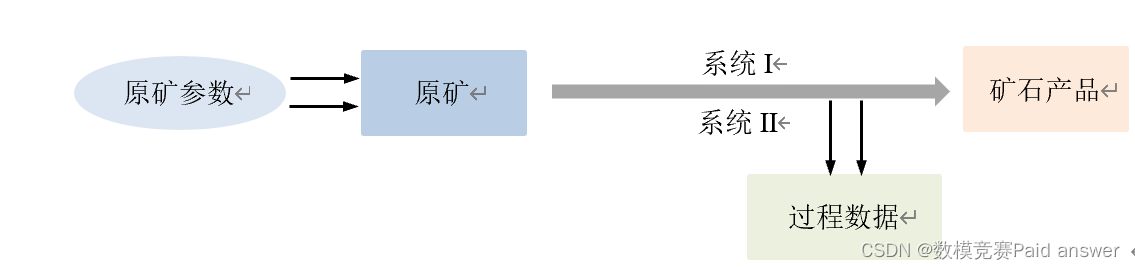
提高矿石加工质量,可以直接或间接地节约不可再生的矿物资源以及加工所需的能源,从而推动节能减排,助力“双碳”目标的实现。矿石加工是一个复杂的过程,在加工过程中,电压、水压、温度作为影响矿石加工的重要因素,直接影响着矿石产品的质量。矿石加工过程如图1所示。某生产车间对于一批原矿进行加工,相关的原矿参数见附件1和附件2。为了方便描述,假设矿石加工过程需要经过系统I和系统II两个环节,两个环节不分先后,其他条件(电压、水压等)保持不变。生产技术人员可以通过传入调温指令,调节温度来改变产品质量。其中系统I和II的温度数据见附件1和附件2。矿石加工过程为2小时整(即:在调节温度2个小时后,可检测得到该调节温度所对应的矿石产品质量的评价指标(A,B,C,D)),假设每次温度调节之后的2个小时内不会传入新的调温指令,附件1和附件2中的温度数据记录了系统的实时温度,调温指令下达后系统温度基本与调温指令设定的温度相同,但是有轻微波动。注:附件1和附件2中,原矿参数和过程数据未给出数据的具体名称,不同类型的数据,采集时间间隔不同。
问题2:根据问题1的结果,利用附件1的数据,假设原矿参数和产品目标质量已知(系统温度未知),请建立数学模型,估计产品目标质量所对应的系统温度。在给定的2022-01-24原矿参数(见附件1)和目标产品质量(见表2)下,给出系统设定温度(假设调温指令设定的温度与系统温度相同)。注意,同一组产品质量可能有多种调温方法都可以得到,请给出可能性最大的系统设定温度,并填入表2。
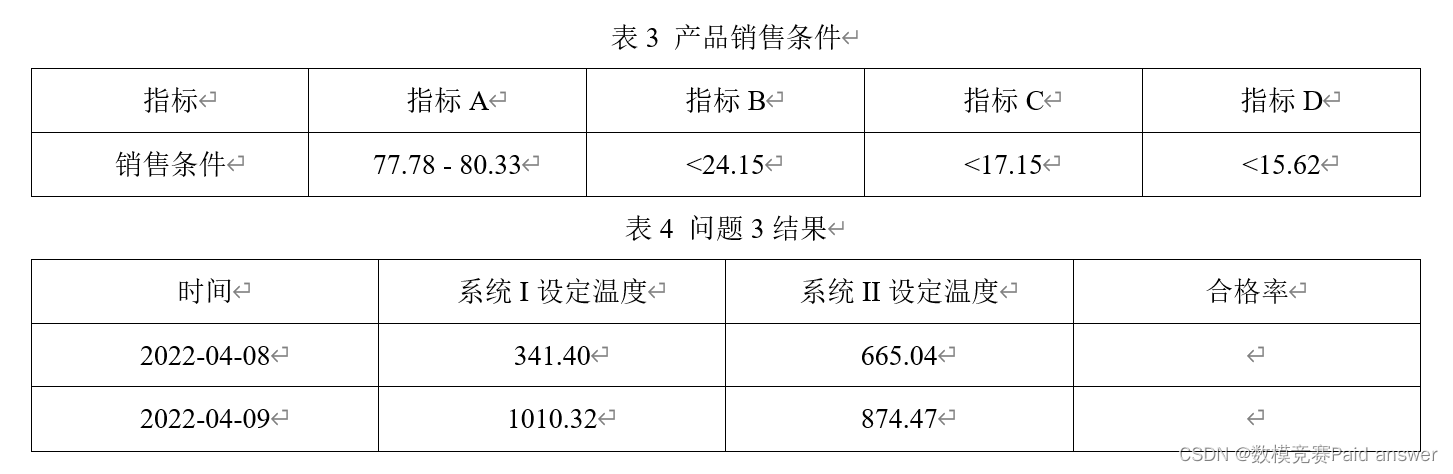
问题3:过程数据是在矿石加工过程中检测得到的(见图1),可以反映原矿质量。由于同一批次(天)的原矿质量有差别,也可能造成在传入相同(或者相近)调温指令后生产出来的产品质量有差别。附件2给出了该生产车间2022-01-25至2022-04-07的生产加工数据及过程数据。表3给出了矿石产品的销售条件,满足销售条件的产品视为合格产品,否则视为不合格产品,假设每单位时间生产的产品数量相同,合格率=合格产品数/产品总数。请建立数学模型,给出指定系统设定温度,预测矿石产品合格率的方法。在给定的2022-04-08和2022-04-09原矿参数、过程数据(见附件2)和系统设定温度(见表4,假设系统温度与调温指令设定的温度相同)下,给出合格率预测结果,填入表4,并建立数学模型对给出的合格率的准确性进行评价。
问题4:根据问题3中的结果,利用附件2的数据,建立数学模型分析在指定合格率的条件下,如何设定系统温度的方法,并完成以下任务:(1)适当的敏感性分析;(2)对结果准确性的分析;(3)判断能否达到表5中给出的2022-04-10和2022-04-11产品的合格率要求(原矿参数和过程数据见附件2),如果可以达到,给出系统设定温度(假设系统温度与调温指令设定的温度相同),并将结果填入表5。
整体求解过程概述(摘要)
目前对矿石加工的质量要求越来越高,因此需要在加工过程中对其进行质量测试,保证加工质量的准确度[1]。本文主要运用非线性预测算法及数据处理相关知识,以矿石加工质量控制问题为研究对象,综合运用线性插值、BP神经网络和数据离散化等方法对问题给出求解的过程和结果。
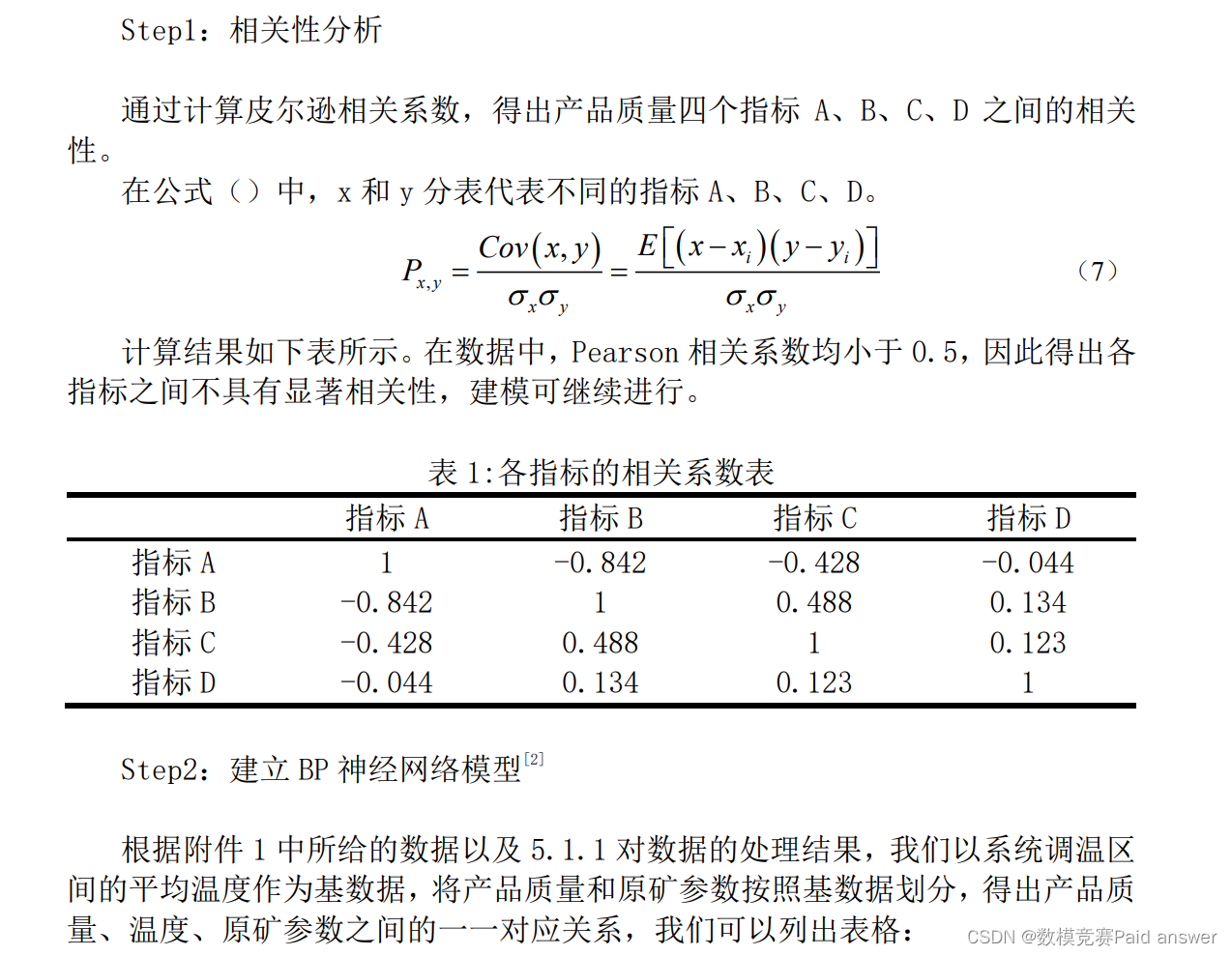
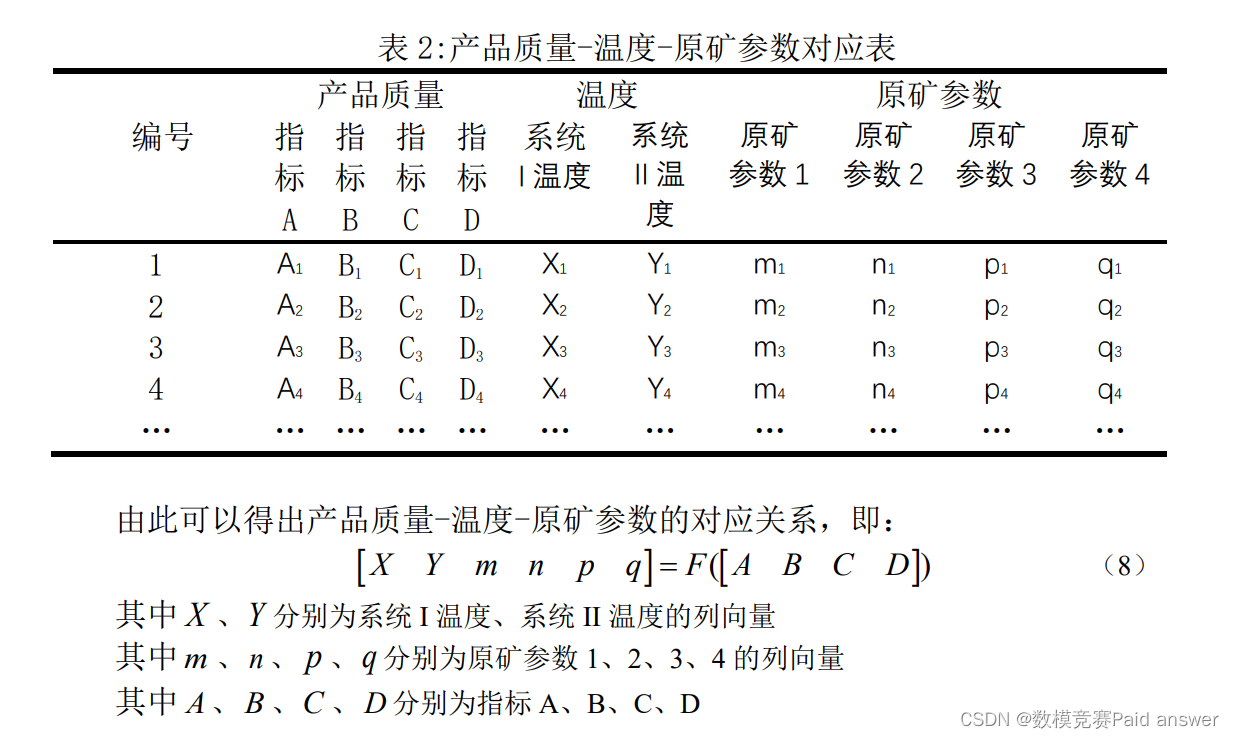
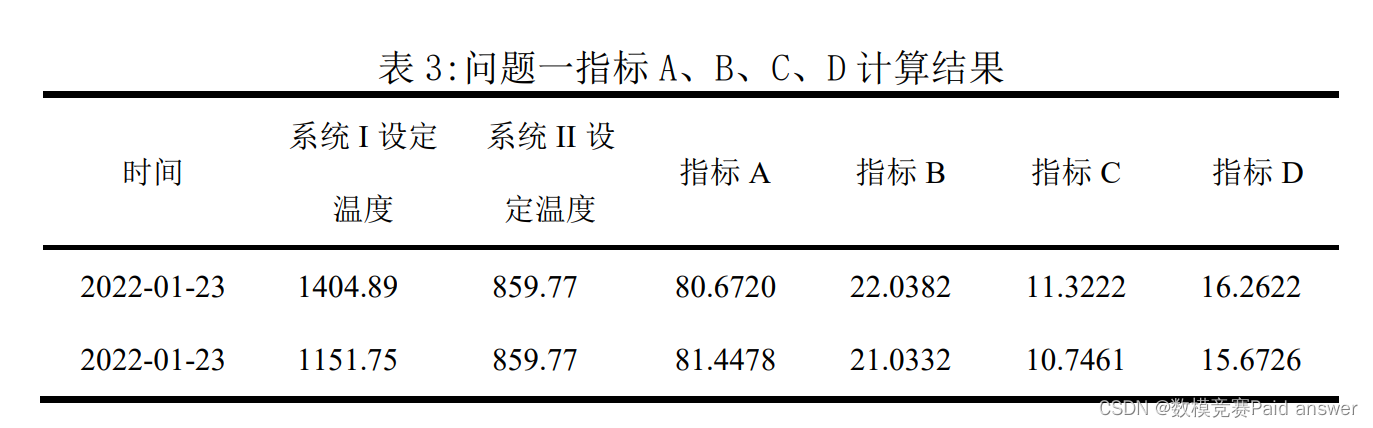
针对问题一,首先根据实际情况使用删除法或线性插值法对数据进行预处理。经过皮尔逊相关系数分析,计算指标A、B、C、D之间的相关性,根据计算结果所得的相关系数表可知,各指标之间不具有显著相关性。根据附件1中所给的数据以及对数据的处理结果,以系统调温区间的平均温度作为基数据,将产品质量和原矿参数按照基数据划分,得出产品质量、温度、原矿参数之间的一一对应关系。选择BP神经网络模型,以系统温度、原矿参数作为输入数据,产品质量作为输出数据,训练神经网络,得到系统温度、原矿参数和产品质量之间的关系。根据题目所给2022-01-23两组系统温度,选择当天原矿参数输入神经网络,输出产品质量结果。
针对问题二,同样采用BP神经网络模型。以原矿参数和产品质量为输入数据,系统温度为输出数据,训练神经网络,得到系统温度与原矿参数、产品质量的关系,根据问题2所给数据预测出可能性最大的系统设定温度。
针对问题三,首先对数据进行线性插值预处理,然后利用神经网络找到产品质量与原矿参数、过程参数、系统温度之间的函数关系。预测出2022-04-08与2022-04-09两天的产品质量,每天24组。再利用题目所给约束条件判断24份产品是否是合格品,计算出每天的合格率。利用K-Fold交叉验证评价合格率的准确性。
针对问题四,在已知合格率的情况下,通过改变系统温度,求解三个小问。本文仍然采用神经网络模型并利用问题三处理好的数据进行求解与分析。
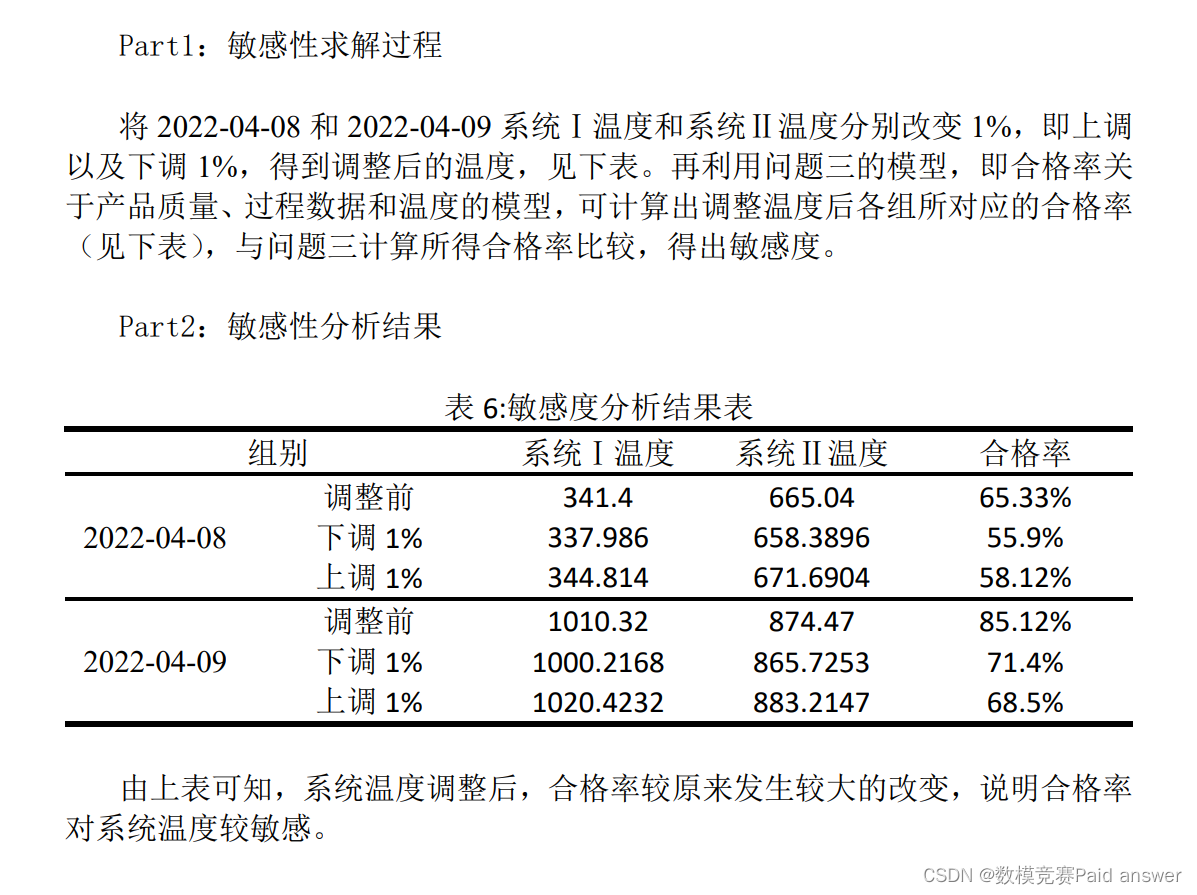
1)第一小问:将题目所给温度分别上调和下调1%,利用神经网络得到调整温度后对应的合格率,与原合格率对比,得出模型的敏感性较强。
2)第二小问:利用2022-01-25至2022-04-07之间的数据输入神经网络后输出模拟合格率,与真实合格率比较,将准确范围设置为误差值在2%以内,得出模型的准确性较高。
3)第三小问:利用2022-01-25至2022-04-09数据及题目所给合格率输入神经网络,输出达到该合格率所需的温度,将该温度及2022-04-10和2022-04-11的其他数据分别输入代码,得出合格率达不到题目所给的80%和99%。
关键词:线性插值 BP神经网络算法 综合评价法
问题分析
问题一的分析
以产品质量为目标函数,原矿参数和系统设定温度为自变量,利用2022-01-13至2022-01-22的生产加工数据建立产品质量与原矿参数和系统设定温度的函数关系模型。对附件1中温度(temperature)和产品质量(quality of the products)的数据进行筛选,对两次转变温度的时间区间内的温度测量值求平均值,对在该时间区间内的有效产品质量数据求平均值,得到一组原矿参数-温度-产品质量的对应关系,利用神经网络模型将其拟合,以预测2022-01-23的产品质量结果。
问题二的分析
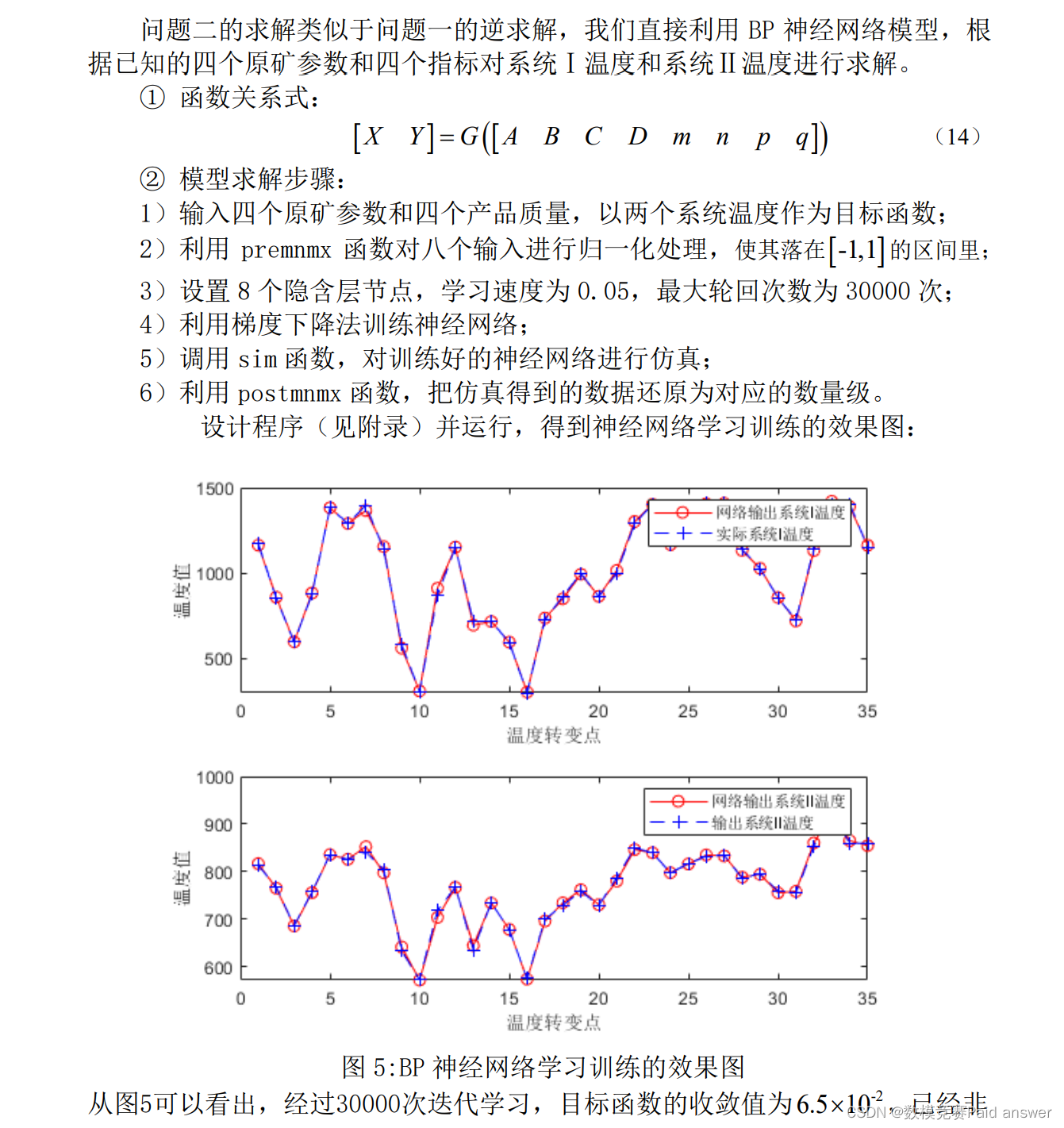
问题二是已知需要达到的结果,推断出得出这样的结果的原因。要求根据指标确定温度,类似于建议问题一模型的逆模型,也可以直接使用bp网络神经来预测。我们需要调整模型为八输入二输出模型,再根据训练好的bp网络神经来反过来预测系统温度。
问题三的分析
问题三需要我们求解2022-04-08和2022-04-09的合格率且合格率=合格产品数/产品总数,此处我们将一次测得的指标A、B、C、D划分为一组,利用一个时间段内测得的所有组产品指标中符合销售条件的组数除以该时间段内被测的总组数代替合格率,为了计算的便捷性,我们选取一天作为多个测量指标的统一值。我们需要将温度、产品质量、原矿参数和过程数据统一为一天记录一次,并通过代码将一天当中测得的产品质量按照销售条件计算出合格率,得到2022-01-25至2022-04-07的合格率。将两个温度数据、四个原矿参数、四个过程数据作为输入,合格率作为输出,利用BP神经网络模型求解,并用神经网络综合法评估合格率的准确性。
问题四的分析
问题四首先需要我们根据合格率确定温度,类似于问题三模型的逆模型,也可以直接使用bp网络神经来预测。我们需要调整模型为一输入二输出模型,再根据训练好的bp网络神经来反过来预测系统温度。
第一小问需要进行敏感性分析,即检验模型结果的可信度。验证当参数有一个小的误差对模型的结果影响也很小时,则说明结果是可信的。所以我们设定温度变化为1%,然后预测它的合格率是否变化过大来判定他们的敏感性。
第二小问和问题三一样采用神经网络综合评价法,比较合格率真实值和训练结果预测值得出准确度。
第三小问利用建立好的神经网络模型训练预测2022-04-10和2022-04-11达到给定合格率需要的系统设定温度,再输入系统设定温度计算合格率,观察是否能达到给定合格率。
模型的建立与求解:
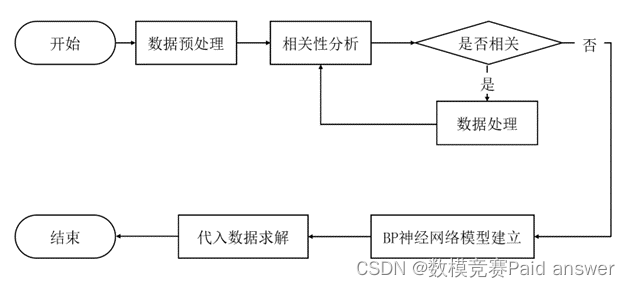
以下为本部分在进行建模时的流程图:
利用 BP 神经网络预测产品质量的模型
Step3:BP神经网络求解
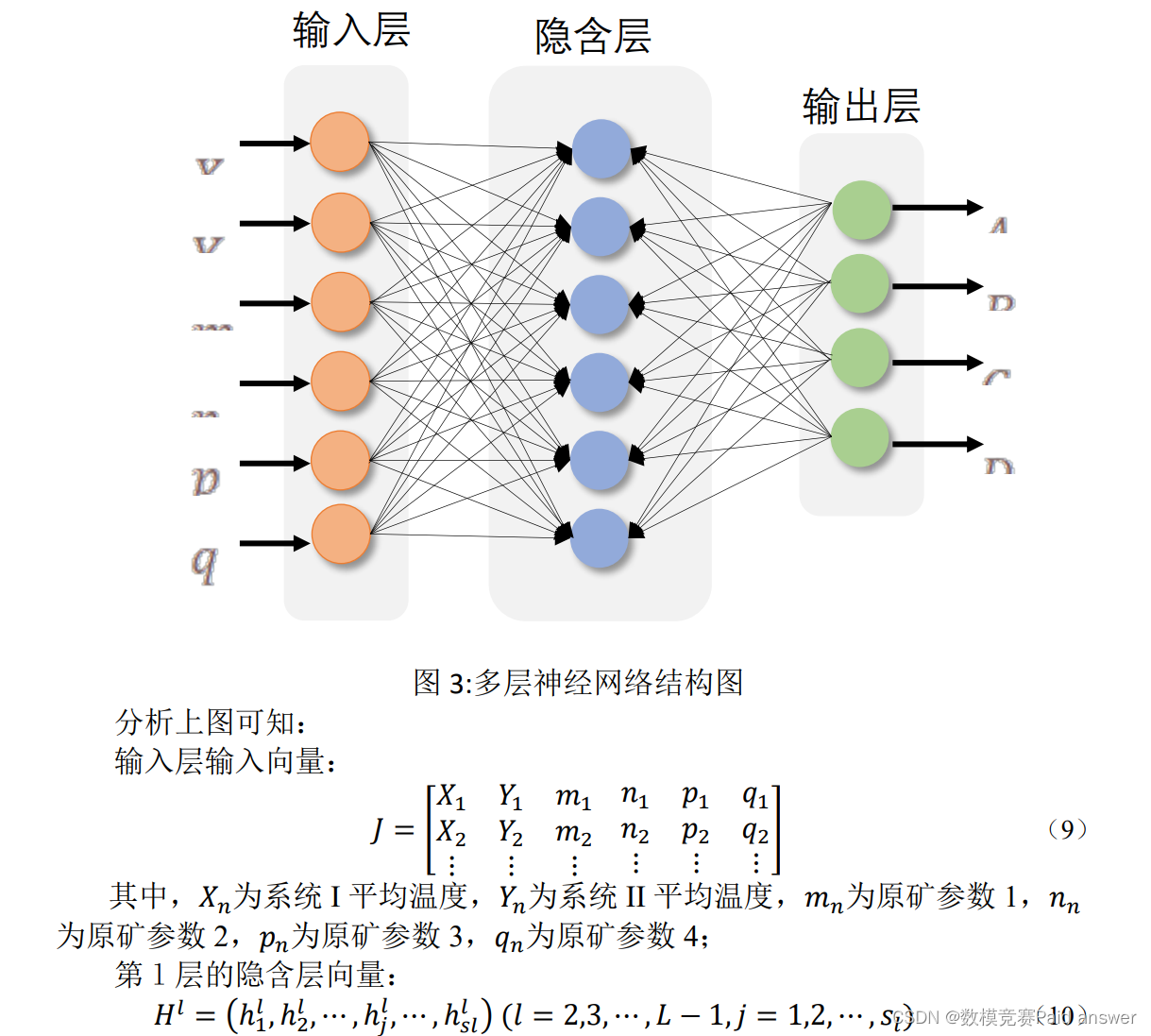
以四个原矿参数、两个系统温度为输入,四个产品质量为输出,利用BP神经网络对数据进行训练,再将待检测数据条件输入,得出结果。
利用BP神经网络求解的过程可分为6个模块处理:
1) 原始数据系统温度和原矿参数的输入;
2) 数据归一化;
3) 网络训练;
4) 对原始数据进行仿真;
5) 将原始数据的仿真结果与已知样本进行对比;
6) 对新数据进行仿真。
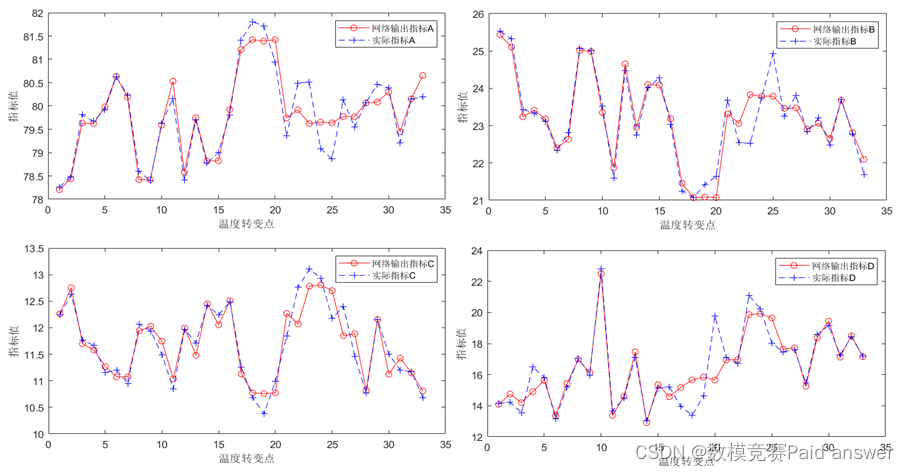
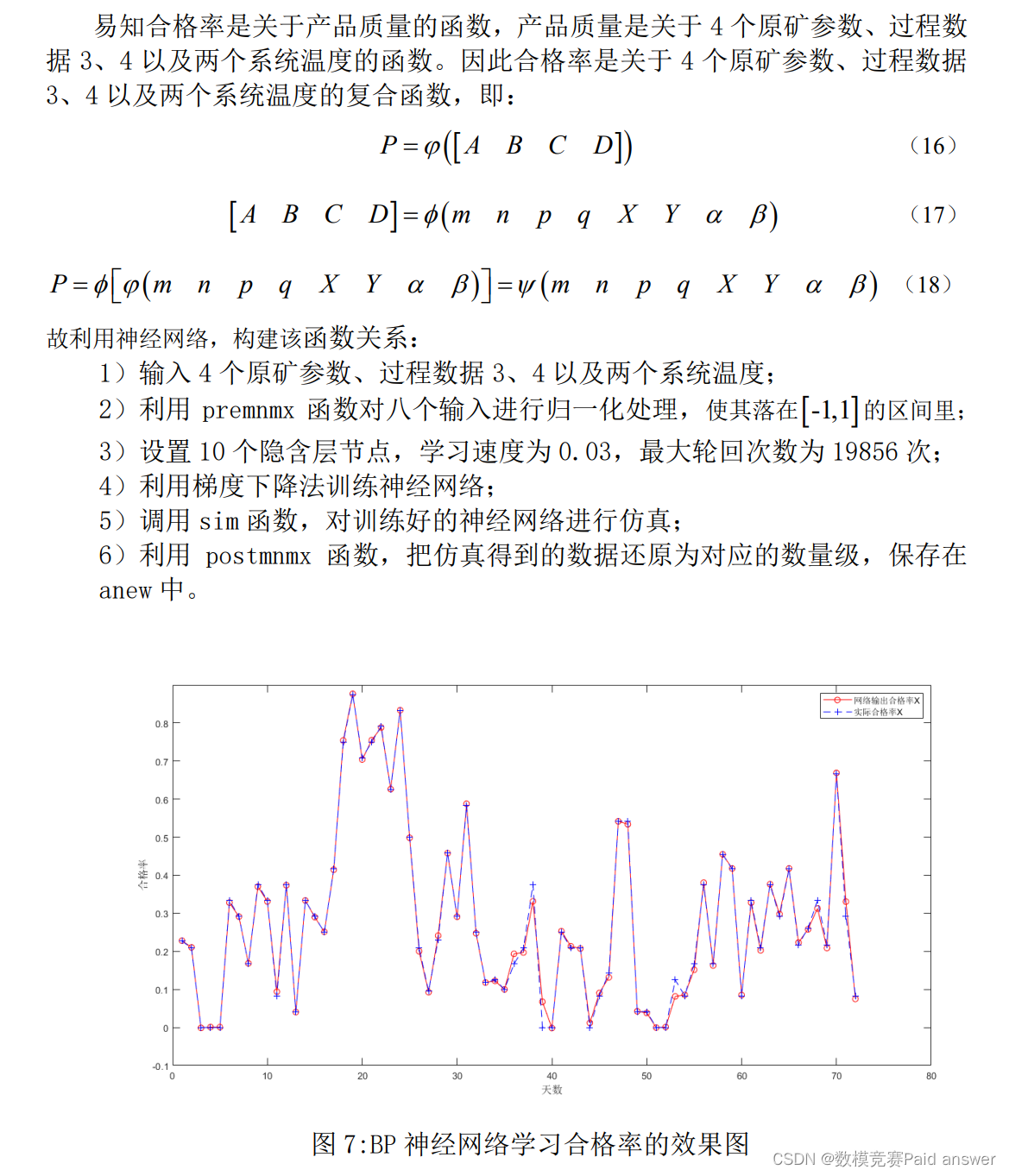
设计程序(见附录)并运行,得到如下图所示:
由上图可知,拟合效果较好。
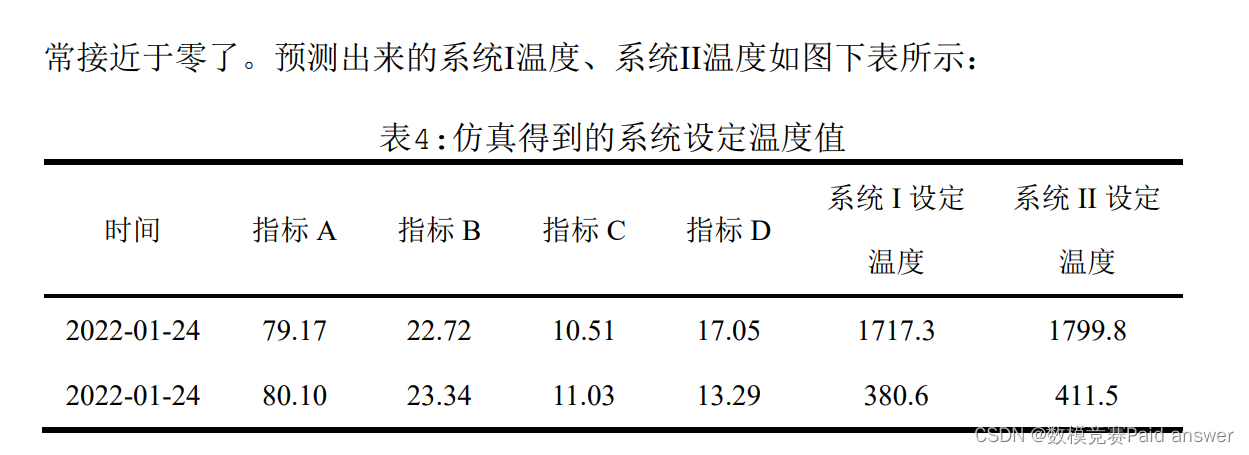
程序运行可以得到结果,如下表所示:
每天合格率的模型
产品质量每隔一小时测一次,一天24次。假设每单位时间生产的产品数量相同,将一天生产的产品总量离散成24份,每一份代表一个单位的产品,每一次产品质量检测对应一个单位的产品质量。在每一天的24份产品中,若四个指标符合销售条件,则记为合格。记录下24份产品中合格的份数,则合格率可定义为:
合格率关于产品质量、过程数据和温度的函数模型
合格率的准确性评价模型
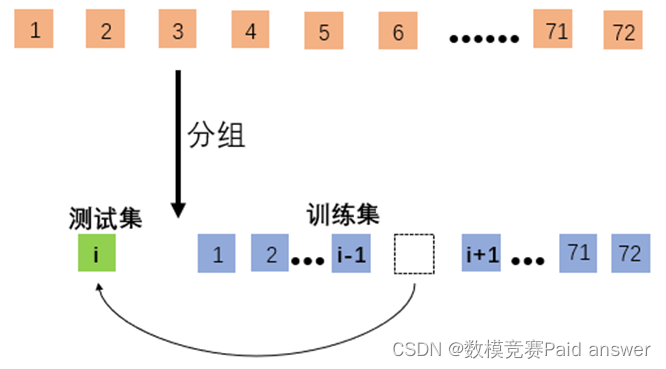
假设合格率的准确性与模型的准确性成正相关,即模型越准确,合格率的计算也越准确。在合格率关于产品质量、过程数据和温度的函数模型中有72组训练数据,将这72组训练数据分成两份,一份是包含71组原数据的训练集,另一组是包含一组原始数据的测试集:
分组方式共有72种, 表示分到测试集的数据是第 天的。利用循环,依次将不同组训练集代入到原神经网络模型中,让其学习训练,预测出测试集的数据,关注到合格率,若预测的测试集的合格率与测试集的合格率满足以下条件,则判定此次神经网络对合格率的预测是正确的,计数器ct=ct+1
敏感性分析
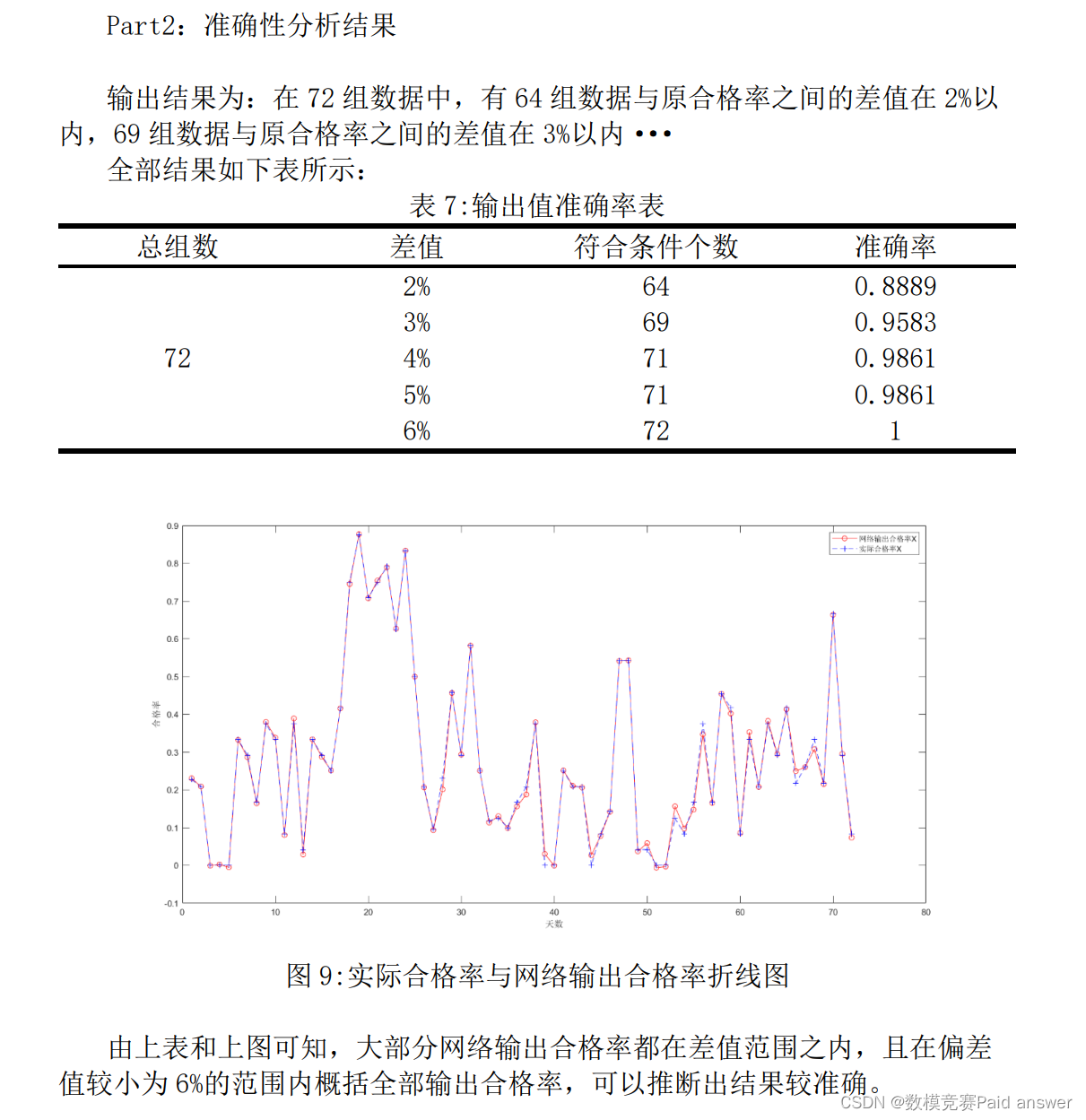
准确性分析
Part1:准确性分析计算过程
为了检验模型的准确性,我们应该比较实际合格率与神经网络训练所得的合格率之间的差值,我们取合格率数值相差2%算作准确。
利用2022-01-25至2022-04-07(见附录表格“问题4”)的数据,将原矿参数1、2、3、4,过程数据1、2、3、4和合格率作为输入数据,系统Ⅰ温度和系统Ⅱ温度作为输出数据,导入神经网络模型代码,得到72个合格率,并与原来的合格率比较,预测值与实际值的差值为预测值减实际值的绝对值除实际值,由此可以求出准确率并分析准确度。
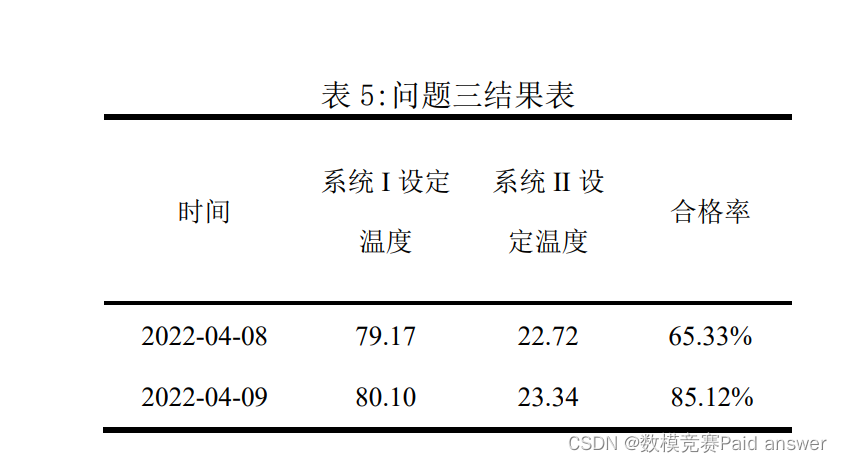
判断能否达到合格率要求
将2022-01-25至2022-04-09之间的原矿参数、过程数据、合格率作为输入数据,系统设定温度作为输出数据,输入到神经网络模型代码中,求出在给定合格率的情况下,对应的系统Ⅰ温度和系统Ⅱ温度。求得系统Ⅰ温度和系统Ⅱ温度分别为1221.2375和850.99.
将2022-04-10和2022-04-11的原矿参数、过程数据和计算得到的系统温度作为输入数据,合格率作为输出数据,求得合格率,合格率分别为45.34%和55,86%。因此得到下表:
全部论文请见下方“ 只会建模 QQ名片” 点击QQ名片即可
问题一程序:
处理数据:
num=xlsread('C:\附件1.xls','温度(temperature)','B2:B14220');
changetem=[];
j=1;
for i=2:1:14219
if abs(num(i)-num(i-1))>20
changetem(j)=i;
j=j+1
end
End
avertem=[];
a=1;
j=1;
for i=1:1:14219
if i==changetem(j)
avertem(j)=mean(num(a:changetem(j)));
a=changetem(j)+1;
j=j+1;
end
end
神经网络代码(问题1):
%原始数据
%系统I温度 (Temperature of system I)(单位:℃)
Wd1=xlsread('C:\Users\admin\Desktop\一小时.xlsx','1','B2:B234');
%系统II温度 (Temperature of system II) (单位:℃)
Wd2=xlsread('C:\Users\admin\Desktop\一小时.xlsx','1','C2:C234');
%原矿参数1 (Mineral parameter 1)
Y1=xlsread('C:\Users\admin\Desktop\一小时.xlsx','1','D2:D234');
%原矿参数2 (Mineral parameter 2)
Y2=xlsread('C:\Users\admin\Desktop\一小时.xlsx','1','E2:E234');
%原矿参数3 (Mineral parameter 3)
Y3=xlsread('C:\Users\admin\Desktop\一小时.xlsx','1','F2:F234');
%原矿参数4 (Mineral parameter 4)
Y4=xlsread('C:\Users\admin\Desktop\一小时.xlsx','1','G2:G234');
%指标A (index A)
zbA=xlsread('C:\Users\admin\Desktop\一小时.xlsx','1','H2:H234');
%指标B(index B)
zbB=xlsread('C:\Users\admin\Desktop\一小时.xlsx','1','I2:I234');
%指标C(index C)
zbC=xlsread('C:\Users\admin\Desktop\一小时.xlsx','J2:J234');
%指标D(index D)
zbD=xlsread('C:\Users\admin\Desktop\一小时.xlsx','1','K2:K234');
p=[Wd1,Wd2,Y1,Y2,Y3,Y4]; %输入数据矩阵
t=[ zbA,zbB,zbC,zbD]; %目标数据矩阵
%②数据归一化
%利用premnmx函数对数据进行归一化
p=p';
t=t';
[pn,minp,maxp,tn,mint,maxt]=premnmx(p,t); % 对于输入矩阵p和输出矩阵t进行归一化处理
dx=[-1,1;-1,1;-1,1;-1,1;-1,1;-1,1]; %归一化处理后最小值为-1,最大值为1
%③网络训练
%BP网络训练
net=newff(dx,[6,9,4],{'tansig','tansig','purelin'},'traingdx'); %建立模型,并用梯度下降法训练.
net.trainParam.show=1000; %1000轮回显示一次结果
net.trainParam.Lr=0.05; %学习速度为0.05
net.trainParam.epochs=50000; %最大训练轮回为50000次
net.trainParam.goal=0.65*10^(-3); %均方误差
net=train(net,pn,tn);%开始训练,其中pn,tn分别为输入输出样本
%④利用训练好的BP网络对原始数据进行仿真
%利用原始数据对BP网络仿真
an=sim(net,pn); %用训练好的模型进行仿真
a=postmnmx(an,mint,maxt); % 把仿真得到的数据还原为原始的数量级;
%⑤将原始数据的仿真结果与已知样本进行对比
%本例因样本容量有限使用训练数据进行测试,通常必须用新鲜数据进行测试
x=1:233;
newk=a(1,:); %取第一行
newh=a(2,:);
newj=a(3,:);
newl=a(4,:);
newk=newk';
newh=newh';
newj=newj';
newl=newl';
figure (4);
subplot(2,2,1);plot(x,newk,'r-o',x,zbA ,'b--+') %绘值指标A对比图;
legend('网络输出指标A','实际指标A');
xlabel('温度转变点');ylabel('指标值');
subplot(2,2,2);plot(x,newh,'r-o',x, zbB,'b--+') %绘制指标B对比图;
legend('网络输出指标B','实际指标B');
xlabel('温度转变点');ylabel('指标值');
subplot(2,2,3);plot(x,newj,'r-o',x, zbC,'b--+');
legend('网络输出指标C','实际指标C');
xlabel('温度转变点');ylabel('指标值');
subplot(2,2,4);plot(x,newl,'r-o',x, zbD,'b--+') %绘制指标D对比图;
legend('网络输出指标D','实际指标D');
xlabel('温度转变点');ylabel('指标值');
pnew=[1404.89 1151.75
859.77 859.77
52.75 52.75
96.87 96.87
46.61 46.61
22.91 22.91]; %2022-1-23相关数据;
pnewn=tramnmx(pnew,minp,maxp); %利用原始输入数据的归一化参数对新数据进行归一化;
anewn=sim(net,pnewn); %利用归一化后的数据进行仿真;
anew=postmnmx(anewn,mint,maxt) %把仿真得到的数据还原为原始的数量级;
问题二程序:
%原始数据
%系统I温度 (Temperature of system I)(单位:℃)
Wd1=xlsread('C:\Users\admin\Desktop\一小时.xlsx','1','B2:B234');
%系统II温度 (Temperature of system II) (单位:℃)
Wd2=xlsread('C:\Users\admin\Desktop\一小时.xlsx','1','C2:C234');
%原矿参数1 (Mineral parameter 1)
Y1=xlsread('C:\Users\admin\Desktop\一小时.xlsx','1','D2:D234');
%原矿参数2 (Mineral parameter 2)
Y2=xlsread('C:\Users\admin\Desktop\一小时.xlsx','1','E2:E234');
%原矿参数3 (Mineral parameter 3)
Y3=xlsread('C:\Users\admin\Desktop\一小时.xlsx','1','F2:F234');
%原矿参数4 (Mineral parameter 4)
Y4=xlsread('C:\Users\admin\Desktop\一小时.xlsx','1','G2:G234');
%指标A (index A)
zbA=xlsread('C:\Users\admin\Desktop\一小时.xlsx','1','H2:H234');
%指标B(index B)
zbB=xlsread('C:\Users\admin\Desktop\一小时.xlsx','1','I2:I234');
%指标C(index C)
zbC=xlsread('C:\Users\admin\Desktop\一小时.xlsx','J2:J234');
%指标D(index D)
zbD=xlsread('C:\Users\admin\Desktop\一小时.xlsx','1','K2:K234');
p=[Y1,Y2,Y3,Y4,zbA,zbB,zbC,zbD]; %输入数据矩阵
t=[ Wd1,Wd2]; %目标数据矩阵
%②数据归一化
%利用premnmx函数对数据进行归一化
p=p';
t=t';
[pn,minp,maxp,tn,mint,maxt]=premnmx(p,t); % 对于输入矩阵p和输出矩阵t进行归一化处理
dx=[-1,1;-1,1;-1,1;-1,1;-1,1;-1,1;-1,1;-1,1]; %归一化处理后最小值为-1,最大值为1
%③网络训练
%BP网络训练
net=newff(dx,[8,7,2],{'tansig','tansig','purelin'},'traingdx'); %建立模型,并用梯度下降法训练.
net.trainParam.show=1000 %1000轮回显示一次结果
net.trainParam.Lr=0.05; %学习速度为0.05
net.trainParam.epochs=5000; %最大训练轮回为50000次
net.trainParam.goal=0.65*10^(-3); %均方误差
net=train(net,pn,tn);%开始训练,其中pn,tn分别为输入输出样本
%④利用训练好的BP网络对原始数据进行仿真
%利用原始数据对BP网络仿真
an=sim(net,pn); %用训练好的模型进行仿真
a=postmnmx(an,mint,maxt); % 把仿真得到的数据还原为原始的数量级;
%⑤将原始数据的仿真结果与已知样本进行对比
%本例因样本容量有限使用训练数据进行测试,通常必须用新鲜数据进行测试
x=1:233;
newk=a(1,:); %取第一行
newh=a(2,:);
newk=newk';
newh=newh';
figure (2);
subplot(2,2,1);plot(x,newk,'r-o',x,Wd1 ,'b--+') %绘值指标A对比图;
legend('网络输出温度X','实际温度X');
xlabel('温度转变点');ylabel('温度值');
subplot(2,2,2);plot(x,newh,'r-o',x,Wd2,'b--+') %绘制指标B对比图;
legend('网络输出温度Y','实际温度Y');
xlabel('温度转变点');ylabel('温度值');
pnew=[ 57.5 57.5
108.62 108.62
44.5 44.5
20.09 20.09
79.17 80.10
22.72 23.34
10.51 11.03
17.05 13.29
]; %2022-1-23相关数据;
pnewn=tramnmx(pnew,minp,maxp); %利用原始输入数据的归一化参数对新数据进行归一化;
anewn=sim(net,pnewn); %利用归一化后的数据进行仿真;
anew=postmnmx(anewn,mint,maxt) %把仿真得到的数据还原为原始的数量级;
%将温度和产品质量统一时间
num=xlsread('C:\Users\admin\Desktop\附件2.xls','温度(temperature)','G2:G14140');
avertem=[];
j=1;
for i=50:60:14019
avertem(j)=mean(num(i:i+119));
j=j+1;
end
avertem=avertem';
%计算每天的平均过程数据
num=xlsread('C:\Users\派大星摘了颗星星\Desktop\附件2(3)(1).xls','过程数据(process parameter)','E1:E616');
avertem=[];
j=1;
for i=1:1:616
if mod(i,8)==0
avertem(j)=(sum(num(i-7:i)))/8;
j=j+1;
else
end
End
%计算合格率
num=xlsread('C:\Users\admin\Desktop\附件2.xls','产品质量(quality of the products)','B1:E1655');
count=0;
circletime=0;
hegelv=[];
j=1;
for i=1:1:22
if (77.78<=num(i,1)<=80.33)&(num(i,2)<24.15)&(num(i,3)<17.15)&(num(i,4)<15.62)
count=count+1;
end
if mod(i,22)==0
disp(count);
hegelv(j)=count/22;
j=j+1;
count=0;
end
end
hegelv=hegelv';
问题三程序:
%第三题评估代码
%原始数据
k=0
for i=1:72
%系统I温度 (Temperature of system I)(单位:℃)
Wd1=xlsread('G:\附件2.xls','原矿参数(mineral parameter)','F2:F73');
%系统II温度 (Temperature of system II) (单位:℃)
Wd2=xlsread('G:\附件2.xls','原矿参数(mineral parameter)','G2:G73');
%原矿参数1 (Mineral parameter 1)
Y1=xlsread('G:\附件2.xls','原矿参数(mineral parameter)','B2:B73');
%原矿参数2 (Mineral parameter 2)
Y2=xlsread('G:\附件2.xls','原矿参数(mineral parameter)','C2:C73');
%原矿参数3 (Mineral parameter 3)
Y3=xlsread('G:\附件2.xls','原矿参数(mineral parameter)','D2:D73');
%原矿参数4 (Mineral parameter 4)
Y4=xlsread('G:\附件2.xls','原矿参数(mineral parameter)','E2:E73');
%指标A (index A)
gc1=xlsread('G:\附件2.xls','原矿参数(mineral parameter)','H2:H73');
%指标B(index B)
gc2=xlsread('G:\附件2.xls','原矿参数(mineral parameter)','I2:I73');
%指标C(index C)
gc3=xlsread('G:\附件2.xls','原矿参数(mineral parameter)','J2:J73');
%指标D(index D)
gc4=xlsread('G:\附件2.xls','原矿参数(mineral parameter)','K2:K73');
hegelv=xlsread('G:\附件2.xls','原矿参数(mineral parameter)','L2:L73');
Wd1y=Wd1(i);
Wd1(i)=[];
Wd2y=Wd2(i);
Wd2(i)=[];
Y1y=Y1(i);
Y1(i)=[];
Y2y=Y2(i);
Y2(i)=[];
Y3y=Y3(i);
Y3(i)=[];
Y4y=Y4(i);
Y4(i)=[];
gc1y=gc1(i);
gc1(i)=[];
gc2y=gc2(i);
gc2(i)=[];
gc3y=gc3(i);
gc3(i)=[];
gc4y=gc4(i);
gc4(i)=[];
hegelvy=hegelv(i);
hegelv(i)=[];
p=[Y1,Y2,Y3,Y4,Wd1,Wd2,gc1,gc2,gc3,gc4]; %输入数据矩阵
t=[ hegelv]; %目标数据矩阵
%②数据归一化
%利用premnmx函数对数据进行归一化
p=p';
t=t';
[pn,minp,maxp,tn,mint,maxt]=premnmx(p,t); % 对于输入矩阵p和输出矩阵t进行归一化处理
dx=[-1,1;-1,1;-1,1;-1,1;-1,1;-1,1;-1,1;-1,1;-1,1;-1,1]; %归一化处理后最小值为-1,最大值为1
%③网络训练
%BP网络训练
net=newff(dx,[10,10,1],{'tansig','tansig','purelin'},'traingdx'); %建立模型,并用梯度下降法训练.
net.trainParam.show=1000 %1000轮回显示一次结果
net.trainParam.Lr=0.05; %学习速度为0.05
net.trainParam.epochs=19856; %最大训练轮回为50000次
net.trainParam.goal=0.65*10^(-3); %均方误差
net=train(net,pn,tn);%开始训练,其中pn,tn分别为输入输出样
%④利用训练好的BP网络对原始数据进行仿真
%利用原始数据对BP网络仿真
an=sim(net,pn); %用训练好的模型进行仿真
a=postmnmx(an,mint,maxt); % 把仿真得到的数据还原为原始的数量级;
%⑤将原始数据的仿真结果与已知样本进行对比
%本例因样本容量有限使用训练数据进行测试,通常必须用新鲜数据进行测试
x=1:71;
newk=a(1,:); %取第
figure (1);
plot(x,newk,'r-o',x,hegelv ,'b--+') %绘值指标A对比图;
legend('网络输出合格率X','实际合格率X');
xlabel('天数');ylabel('合格率');
pnew=[ Y1y
Y2y
Y3y
Y4y
Wd1y
Wd2y
gc1y
gc2y
gc3y
gc4y
]; %2022-1-23相关数据;
pnewn=tramnmx(pnew,minp,maxp); %利用原始输入数据的归一化参数对新数据进行归一化;
anewn=sim(net,pnewn); %利用归一化后的数据进行仿真;
anew=postmnmx(anewn,mint,maxt) %把仿真得到的数据还原为原始的数量级;
if abs(anew-hegelvy)<0.03
k=k+1;
end
%disp(k)
end
disp(k/72)
问题四程序:
%原始数据
%系统I温度 (Temperature of system I)(单位:℃)
Wd1=xlsread('C:\Users\admin\Desktop\附件2.xls','原矿参数(mineral parameter)','F2:F73');
%系统II温度 (Temperature of system II) (单位:℃)
Wd2=xlsread('C:\Users\admin\Desktop\附件2.xls','原矿参数(mineral parameter)','G2:G73');
%原矿参数1 (Mineral parameter 1)
Y1=xlsread('C:\Users\admin\Desktop\附件2.xls','原矿参数(mineral parameter)','B2:B73');
%原矿参数2 (Mineral parameter 2)
Y2=xlsread('C:\Users\admin\Desktop\附件2.xls','原矿参数(mineral parameter)','C2:C73');
%原矿参数3 (Mineral parameter 3)
Y3=xlsread('C:\Users\admin\Desktop\附件2.xls','原矿参数(mineral parameter)','D2:D73');
%原矿参数4 (Mineral parameter 4)
Y4=xlsread('C:\Users\admin\Desktop\附件2.xls','原矿参数(mineral parameter)','E2:E73');
%指标A (index A)
gc1=xlsread('C:\Users\admin\Desktop\附件2.xls','原矿参数(mineral parameter)','H2:H73');
%指标B(index B)
gc2=xlsread('C:\Users\admin\Desktop\附件2.xls','原矿参数(mineral parameter)','I2:I73');
%指标C(index C)
gc3=xlsread('C:\Users\admin\Desktop\附件2.xls','原矿参数(mineral parameter)','J2:J73');
%指标D(index D)
gc4=xlsread('C:\Users\admin\Desktop\附件2.xls','原矿参数(mineral parameter)','K2:K73');
hegelv=xlsread('C:\Users\admin\Desktop\附件2.xls','原矿参数(mineral parameter)','L2:L73');
p=[Y1,Y2,Y3,Y4,gc1,gc2,gc3,gc4, Wd1,Wd2]; %输入数据矩阵
t=[hegelv]; %目标数据矩阵
%②数据归一化
%利用premnmx函数对数据进行归一化
p=p';
t=t';
[pn,minp,maxp,tn,mint,maxt]=premnmx(p,t); % 对于输入矩阵p和输出矩阵t进行归一化处理
dx=[-1,1;-1,1;-1,1;-1,1;-1,1;-1,1;-1,1;-1,1;-1,1;-1,1]; %归一化处理后最小值为-1,最大值为1
%③网络训练
%BP网络训练
net=newff(dx,[10,10,1],{'tansig','tansig','purelin'},'traingdx'); %建立模型,并用梯度下降法训练.
net.trainParam.show=1000 %1000轮回显示一次结果
net.trainParam.Lr=0.05; %学习速度为0.05
net.trainParam.epochs=19856; %最大训练轮回为50000次
net.trainParam.goal=0.65*10^(-3); %均方误差
net=train(net,pn,tn);%开始训练,其中pn,tn分别为输入输出样本
%④利用训练好的BP网络对原始数据进行仿真
%利用原始数据对BP网络仿真
an=sim(net,pn); %用训练好的模型进行仿真
a=postmnmx(an,mint,maxt); % 把仿真得到的数据还原为原始的数量级;
%⑤将原始数据的仿真结果与已知样本进行对比
%本例因样本容量有限使用训练数据进行测试,通常必须用新鲜数据进行测试
x=1:72;
newk=a(1,:); %取第一行
newk=newk';
figure (1);
plot(x,newk,'r-o',x,hegelv ,'b--+') %绘值指标A对比图;
legend('网络输出合格率X','实际合格率X');
xlabel('天数');ylabel('合格率');
count=0;
zhunquelv=0;
for i=1:1:72
if abs(newk(i)-hegelv(i))<0.02
count=count+1;
end
end
zhunquelv=count/72;
disp(count);
disp(zhunquelv);