SLAM基础——IMU传感器（IMU误差模型、IMU离散积分）

1. IMU测量模型及运动模型

1.1 加速度计工作原理

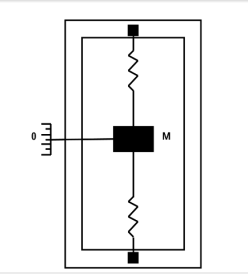
测量原理可以用一个简单的质量块 + 弹簧 + 指示计来表示。
加速度计测量值 $a_m$ 为质量块的加速度，其受到弹簧的拉力为 $f$ 。有：
$a_m=\frac{f}{m}=a-g$ $f$ 弹簧拉力， $a$ 物体在惯性系下的加速度， $g$ 重力加速度。
MEMS 加速度计利用电容或者电阻桥来等原理来测量 $a_m$ 。
在这里插入图片描述

1.2 加速度测量模型

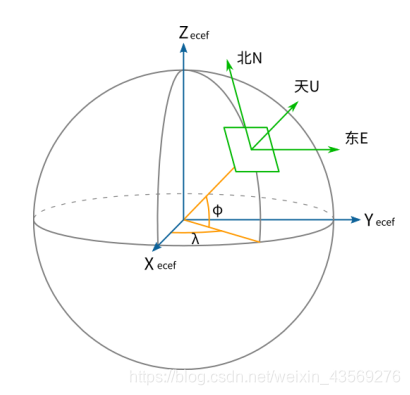
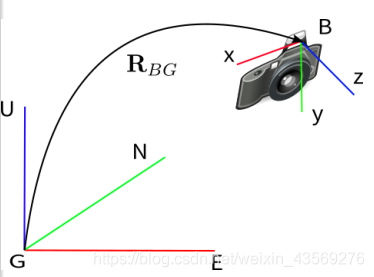
由于地球重力的作用，加速度计有一个以地球坐标为基准的固定的坐标系，成为东北天（ENU，East North Up）坐标系。如下图所示：
在这里插入图片描述
该坐标系上有地球重力加速度： $g=(0,0,-9.81)^T$
假设IMU的本体坐标系和 ENU坐标系重合，则有旋转矩阵 $R_ib=I$ ，静止时有：传感器本身的加速度 $a = 0$ ，其测量加速度 $a_m=-g$ 。自由落体时有： $a=g,a_m=0$ 。

1.3 MEMS陀螺仪工作原理

陀螺仪主要用来测量物体的旋转角速度，按测量原理分有振动陀
螺，光纤陀螺等。
低端 MEMS 陀螺上一般采用振动陀螺原理，通过测量科氏力（ Coriolis
force ）来间接得到角速度。

2. **IMU误差模型

2.1 确定性误差

一、加速度偏置Bias：
理论上，当没有外部作用时，IMU传感器的输出应该为 0。但是实际数据中存在一个零偏 b，这个偏置在三个轴上都存在，是一个三维的偏置。加速度计bias对位姿估计的影响为：
$v_{err} = b^at, \ p_{err} = \frac{1}{2}b^at^2$
该偏置对时间的一阶积分为速度，二阶积分为位移，随着时间的增加，该偏置对速度和位移计算结果的影响会随着积分时间的增加而越来越大。
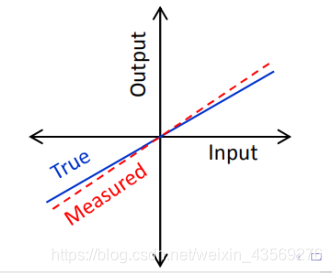
二、比例Scale：
scale是实际数值和传感器输出值之间的比值。在这里插入图片描述
由于传感器的特性，从传感器测量到输出数据，要经过ADC，数据转换中导致实际输出数据略小于测量数据。
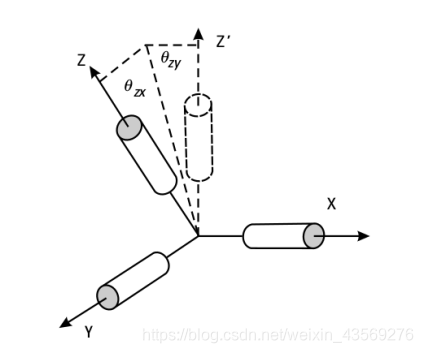
三、Nonorthogonality/Misalignment Errors：
多轴IMU传感器制作的时候，由于制作工艺的问题，会使 $x y z$ 轴可能不垂直，这种不垂直导致该轴的量会对其他两个轴都有影响。如下图所示，z轴不与x,y轴垂直，其测量会在x,y轴上有分量。
在这里插入图片描述
这样，每一个轴的加速度实际值 $l_a$ 与测量值 $a$ 之间具有如下关系：
$\begin{cases} l_{ax}=a_x s_{xx}+a_y m_{xy}+a_z m_{xz} \\ l_{ay}=a_x m_{yx}+a_y s_{yy}+a_z m_{yz} \\ l_{ax}=a_x m_{zx}+a_y m_{zy}+a_z s_{zz} \end{cases} 即 \begin{bmatrix} l_{ax} \\ l_{ax} \\l_{ax} \end{bmatrix} = \begin{bmatrix} s_{xx} &m_{xy} &m_{xz} \\ m_{yx} &s_{yy} &m_{yz} \\ m_{zx} &m_{zy} &s_{zz} \end{bmatrix} \begin{bmatrix} a_x \\ a_y \\ a_z \end{bmatrix}$
其中 $s$ 为 scale， $m$ 为Misalignment Error
四、其他确定性误差：

Run-to-Run Bias/Scale Factor
In Run （Stablity）Bias/Scale Factor
Temperature-Depended Bias/Scale Factor

2.2 确定性误差的标定

2.3 随机误差

一、高斯白噪声：
IMU数据连续时间上受到一个均值为 0，方差为 $\sigma$ ，各个时刻之间独立的高斯过程 $n (t)$ ：
$\\ E[n(t_1)n(t_2)]=\sigma^2 \delta (t_1-t_2)$
其中 $\delta(·)$ 表示狄拉克函数。该函数只有在 $t_1=t_2$ 时才等于1，其他时刻均等于0。
二、Bias随机游走
通常用维纳过程（wiener process）来建模bias时间连续变化的过程，离散时间下称之为随机游走。
这里假设偏置 $b$ 的导数为高斯白噪声，即 $\dot{b}(t) = n_b(t) = \sigma_b w(t)$ ,其中 $w$ 是方差 $\sigma=1$ 的白噪声。

3. **IMU数学模型

3.1 加速度计的误差模型

在这里插入图片描述
如图，假设固有导航系为东北天（ENU）坐标系，该坐标系的重力加速度为 $g^G=(0,0,-9.81)^T$ 。则理论的传感器测量值为：
$a_m^b = R_{BG}(a^G-g^G)$ 假设尺度因子为 $S_a$ ，高斯白噪声为 $n_a$ ，随机游走误差为 $b_a$ ，则实际测量值应为：
$a_m^b = S_a R_{BG} (a^G-g^G) + n^a +b^a$ 通常情况下，我们忽略尺度因子的影响，假设其为单位阵，即 $S_a = I$ 。

3.2 陀螺仪的误差模型

假设尺度因子为 $S_g$ ，高斯白噪声为 $n^g$ ，随机游走误差为 $b^g$ ，陀螺仪的误差模型如下：
$\omega_m^b = S_g \omega^b + n^g + b^g$ 低端传感器，考虑加速度对陀螺仪的影响，即 g-灵敏度：
$\omega_m^b = S_g \omega^b + s_{ga}a^b + n^g + b^g$ 陀螺仪受四种噪声的影响分别如下图所示：
在这里插入图片描述

3.3 VIO中的IMU模型

在ENU坐标系中，忽略尺度因子（scale）的影响，只考虑白噪声和 bias随机游走：
$\tilde{\omega}^b = \omega^b + b^g + n^g \\ \tilde{a}^b = q_{bw}(a^w+g^w) + b^a + n^a$ 上标 $g$ 表示 gyro， $a$ 表示 acc， $w$ 表示在世界坐标系world， $b$ 表示imu本体坐标系body。IMU的真实值为 $\omega,a$ ，测量值为 $\tilde{\omega},\tilde{a}$
P(ose),v(elocity),q(uaternion) 对时间的导数可写成：
$\dot{P}_{wb_t} = \mathrm{v}_t^w \\ \dot{\mathrm{v}}_t^w = a_t^w \\ \dot{q}_{wb_t} = q_{wb_t} \otimes \begin{bmatrix} 0 \\ \frac{1}{2}\omega^{b_t}\end{bmatrix}$

4. 运动模型的离散积分

4.1 连续时间下的IMU运动模型

根据上面的导数关系，可以从第 i 时刻的PVQ，通过对IMU测量值的积分，得到第 j 时刻的PVQ：
$P_{wb_j} = P_{wb_i} + \mathrm{v}_i^w \Delta t + \iint_{t\in[i,j]}(q_{wb_t}a^{b_t} - g^w)dt^2 \\ \mathrm{v}_j^w = \mathrm{v}_i^w + \int_{t\in[i,j]} (q_{wb_t}a^{b_t}-g^w)dt \\ q_{wb_j} = \int_{t \in [i,j]}q_{wb_i} \otimes \begin{bmatrix} 0 \\ \frac{1}{2} \omega^{b_t} \end{bmatrix} dt$

4.2离散时间下的IMU运动模型

4.2.1 欧拉法

使用欧拉法，即两个相邻时刻 $k$ 到 $k + 1$ 的位姿用第 $k$ 时刻的测量值 $a,\omega$ 来计算：
$P_{wb_{k+1}} = P_{wb_k} + \mathrm{v}_k^w \Delta t + \frac{1}{2} a_{k+1} \Delta t^2 \\ \mathrm{v}_{k+1}^{w} = \mathrm{v}_k^w + a_{k+1} \Delta t \\ q_{wb_{k+1}} = q_{wb_k} +\dot{q}_{wb_k} \Delta t = q_{wb_k} \otimes \begin{bmatrix} 1 \\ 0\end{bmatrix} + q_{wb_k} \otimes \begin{bmatrix} 0 \\ \frac{1}{2}\omega_{k+1} \Delta t \end{bmatrix} = q_{wb_k} \otimes \begin{bmatrix} 1 \\ \frac{1}{2}\omega_{k+1} \Delta t \end{bmatrix}$ 其中 $a_{k+1} = q_{wb_k}(a^{b_k}-b_k^a) - g^w \\ \omega_{k+1} = \omega^{b_k} - b_k^g$ 式中 $b_k^a, b_k^g$ 为陀螺仪的偏置 bias。

在这里插入图片描述

4.2.2 中值法

使用中值法(mid-point)，相邻两个时刻 $k$ 到 $k + 1$ 的位姿是用两个时刻测量值 $a，\omega$ 的平均值来计算。()
$P_{wb_{k+1}} = P_{wb_k} + \mathrm{v}_k^w \Delta t + \frac{1}{2}a_{k+1} \Delta t^2 \\ \mathrm{v}_{k+1}^{w} = \mathrm{v}_k^w + a_{k+1} \Delta t \\ q_{wb_{k+1}} = q_{wb_k} \otimes \begin{bmatrix} 1 \\ \frac{1}{2}\omega_{k+1} \Delta t \end{bmatrix}$ 其中 $a_{k+1} = \frac{1}{2}[ q_{wb_k}(a^{b_k}-b_k^a) - g^w + q_{wb_{k+1}}(a^{b_{k+1}}-b_k^a) - g^w] \\ \omega_{k+1} = \frac{1}{2} [(\omega^{b_k} - b_k^g) + (\omega^{b_{k+1}} - b_k^g)]$

**4.3 离散积分代码

4.3.1 欧拉积分

double dt = param_.imu_timestep;	//时间间隔 dt
Eigen::Vector3d Pwb = init_twb_;    //IMU测量的初始位置 position
Eigen::Quaterniond Qwb(init_Rwb_);  //IMU测量的初始旋转 rotation
Eigen::Vector3d Vw = init_velocity_;//IMU测量的初始速度 v
Eigen::Vector3d gw(0,0,-9.81);    // ENU frame 东北天坐标系，重力加速度为-9.81

for (int i = 1; i < imudata.size(); ++i)
{
	
	MotionData imupose = imudata[i];//IMU的测量数据 -- 三轴加速度，三轴角速度
	
	Eigen::Quaterniond dq;
	Eigen::Vector3d dtheta_half =  imupose.imu_gyro * dt /2.0;
	dq.w() = 1;
	dq.x() = dtheta_half.x();
	dq.y() = dtheta_half.y();
	dq.z() = dtheta_half.z();
	dq.normalize();
	/// imu 动力学模型 欧拉积分
	
	Eigen::Vector3d acc_w = Qwb * (imupose.imu_acc) + gw;  // aw = Rwb * ( acc_body - acc_bias ) + gw
	Qwb = Qwb * dq;
	Pwb = Pwb + Vw * dt + 0.5 * dt * dt * acc_w;
	Vw = Vw + acc_w * dt;
}

4.3.2 中值积分代码

double dt = param_.imu_timestep;	//时间间隔 dt
Eigen::Vector3d Pwb = init_twb_;    //IMU测量的初始位置 position
Eigen::Quaterniond Qwb(init_Rwb_);  //IMU测量的初始旋转 rotation
Eigen::Vector3d Vw = init_velocity_;//IMU测量的初始速度 v
Eigen::Vector3d gw(0,0,-9.81);    // ENU frame 东北天坐标系，重力加速度为-9.81
//IMU第一帧数据：
Eigen::Vector3d LastAcc = imudata[0].imu_acc;
Eigen::Vector3d LastTheta = imudata[0].imu_gyro;
for (int i = 1; i < imudata.size(); ++i)
{
		MotionData imupose = imudata[i];

			//由k-1次数据与k次数据得到用于积分的 oemga
		Eigen::Vector3d omega_w = (LastTheta + imupose.imu_gyro) / 2.0;
			//delta_q = [1 , 1/2 * thetax , 1/2 * theta_y, 1/2 * theta_z]
		Eigen::Quaterniond dq;
		Eigen::Vector3d dtheta_half =  omega_w * dt /2.0;
		dq.w() = 1;
		dq.x() = dtheta_half.x();
		dq.y() = dtheta_half.y();
		dq.z() = dtheta_half.z();
		dq.normalize();
		// 记录上一时刻的Qwb，即公式中的Qwb
		Eigen::Quaterniond Qwb_last = Qwb;
		// 更新Qwb，Qwb k+1
		Qwb = Qwb * dq;
		//　imu 动力学模型　参考svo预积分论文
		//由k-1次数据与k次数据得到用于积分的 acc
		Eigen::Vector3d acc_w = (Qwb_last * LastAcc + gw + Qwb * (imupose.imu_acc) + gw) / 2.0;
		
		Pwb = Pwb + Vw * dt + 0.5 * dt * dt * acc_w;
		Vw = Vw + acc_w * dt;

		//迭代，积分完后记录此次测量为k-1次测量
		LastAcc = imupose.imu_acc;
		LastTheta = imupose.imu_gyro;
}