1. 相机畸变及其数学模型

畸变类型

相机畸变主要分为两种：

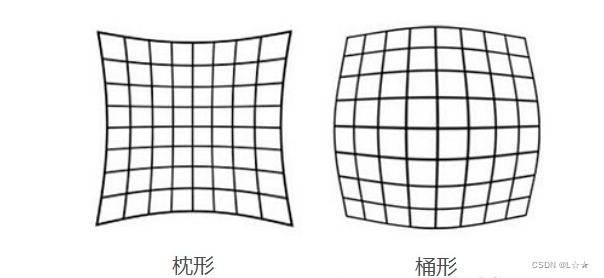
• 径向畸变（枕形、桶形）：光线在远离透镜中心的地方 比 靠近透镜中心的地方 更加弯曲。
• 切向畸变：透镜不完全平行于图像平面，即sensor在安装时与镜头之间的角度不准。

畸变数学模型

径向畸变

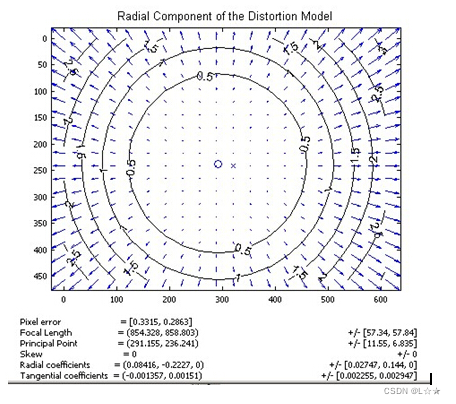
成像仪 光轴中心的畸变为$0$，沿着镜头半径方向 越靠近边缘，畸变越严重。

畸变的数学模型可以用主点（principle point）周围的泰勒级数展开式的前几项来进行描述。

• 通常使用前两项和，即$k_1$和$k_2$

• 对于畸变很大的镜头，如鱼眼镜头，需要增加第三项$k_3$来进行描述。

成像仪上的某点，根据其在径向方向上的分布位置，调节公式为：

$$\hat{x}=x(1+k_1{r}^2+k_2{r}^4+k_3{r}^6)$$

$$\hat{y}=y(1+k_1{r}^2+k_2{r}^4+k_3{r}^6)$$

公式中：

$(\hat{x},\hat{y})$——畸变后的归一化图像坐标

$(x，y)$——无畸变的归一化的图像坐标

$r$——图像像素点到图像中心点的距离，即为：$r^2=x^2+y^2$

径向畸变的偏移示意图

切向畸变

切向畸变是由于透镜本身与相机传感器平面（成像平面）或图像平面不平行而产生的，这种情况多是由于透镜被粘贴到镜头模组上的安装偏差导致

畸变可以由两个额外的参数$p_1$、$p_2$来描述：

$$\hat{x}=x+[2p_{1}xy+p_2(r^2+2x^2)]$$

$$\hat{y}=y+[2p_{2}xy+p_1(r^2+2y^2)]$$

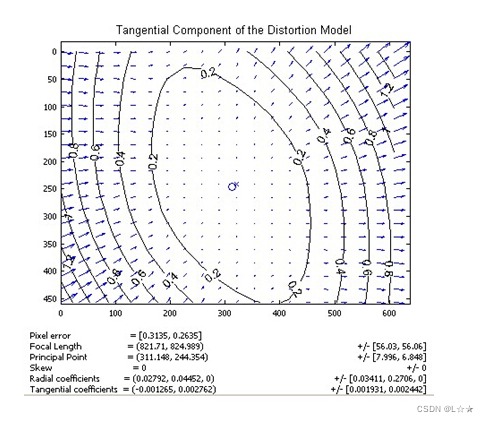
大体上，切向畸变的畸变位移相对于左下——右上角的连线是对称的，说明该镜头在垂直于该方向上有一个旋转角度。

切向畸变的偏移示意图

畸变数学模型总结

径向畸变和切向畸变中，一共有5个畸变参数，OpenCV中他们被排列为一个$5\times 1$的矩阵，依次包含$k_1$、$k_2$、$p_1$、$p_2$、$k_3$，经常被定义为Mat矩阵的形式，如Mat distCoeffs = Mat(1, 5, CV_32FC1, Scalar::all(0));

上述5个参数就是相机标定中需要的相机的5个畸变参数，求得这5个参数后，就可以矫正由镜头畸变引起的图像的变形失真。

因此，包含径向畸变和切向畸变的总体畸变模型：

$$\hat{x}=x(1+k_1{r}^2+k_2{r}^4+k_3{r}^6)+[2p_{1}xy+p_2(r^2+2x^2)]$$

$$\hat{y}=y(1+k_1{r}^2+k_2{r}^4+k_3{r}^6)+[2p_{2}xy+p_1(r^2+2y^2)]$$

其中，

$(\hat{x},\hat{y})$——畸变后的归一化图像坐标

$(x，y)$——无畸变的归一化的图像坐标

$r$——图像像素点到图像中心点的距离，即为：$r^2=x^2+y^2$

$k_1$、$k_2$、$p_1$、$p_2$、$k_3$——畸变参数