1. 引言

在数字信号处理领域，数字滤波器的高效实现一直是研究和实践的重点。当前，有多种编程语言可供选择，如C语言、Matlab语言与Python语言，即使如Python与Matlab有实现数字滤波器的库函数，但 Python 和 Matlab 在数字滤波器实现方面都存在着不容忽视的缺点。

Python是一种解释型语言，其代码在运行时需要通过解释器逐行翻译并执行，执行效率低。虽然 Python 有高效的数值计算库（如 Numpy），但在底层计算上，由于解释过程的存在，会引入一定的开销。例如，在同样的 FIR 数字滤波器实现中，Python 的循环结构（即使是使用了 Numpy 的向量化操作）在执行速度上通常比 C 语言慢几倍到几十倍不等，特别是当信号长度很长时，这种性能差距会进一步拉大。此外，由于Python自动内存管理在处理大型信号集时易浪费内存、产生碎片，且在硬件控制上较弱，对嵌入式等资源受限硬件平台适应性差。

Matlab 虽有丰富信号处理库，这使得它在快速原型开发方面具有一定优势。然而，Matlab高度依赖自身软件环境，这意味着要运行 Matlab 编写的数字滤波器程序，必须安装完整的 Matlab 软件。这种依赖性极大地限制了程序的可移植性，使得在不同的操作系统或硬件平台上部署变得复杂且困难。而且，将 Matlab 程序转化为独立的可执行应用程序的过程复杂且效率不高，这在实际的工程应用中会带来诸多不便。

相比之下， C 语言优势显著。C语言编译后直接运行，执行效率高，能快速处理滤波器的数学运算。C 语言有精细内存管理，可按需分配释放内存，适合资源有限环境。它还便于硬件控制，可直接访问寄存器和设置参数，可移植性也很好。因此，使用 C 语言实现数字滤波器具有重要意义，下面将介绍其实现方法。

2. 滤波器算法结构

2.1 滤波器系数的获取

滤波器函数的作用是对信号进行处理，以去除或减少不需要的频率成分，同时保留或增强有用的信号部分。不同类型的滤波器能够实现不同的效果，主要分为以下几类：

• 低通滤波器（Low-pass filter）：只允许低频成分通过，抑制高频成分。适用于去除高频噪声，常用于平滑信号。
• 高通滤波器（High-pass filter）：只允许高频成分通过，抑制低频成分。常用于去除慢变化的信号成分，如去除信号中的趋势或偏移。
• 带通滤波器（Band-pass filter）：允许特定频段的信号通过，抑制高于或低于该频段的成分。用于提取特定频段的信号成分。
• 带阻滤波器（Band-stop filter）：阻止特定频段的信号通过，允许其他频率通过。常用于消除电源干扰频率（如50Hz或60Hz）等。

由于每种类型的滤波器设计目标和频率范围不同，因此计算得到的滤波器系数也不同。设计滤波器系数的手动计算可能非常复杂，因此通常使用信号处理软件（如MATLAB、Python中的scipy.signal库）来自动生成所需的滤波器系数。例如:

• Matlab代码

  %% 使用Matlab获取带通滤波器系数
  % 设定参数
  Fs = 250;             % 采样率 (Hz)
  low_cutoff_bandpass = 4;       % 带通滤波器的低频截止 (Hz)
  high_cutoff_bandpass = 40;     % 带通滤波器的高频截止 (Hz)
  order = 4;            % 滤波器阶数
  
  % 归一化截止频率
  low_normalized_bandpass = low_cutoff_bandpass / (Fs / 2);
  high_normalized_bandpass = high_cutoff_bandpass / (Fs / 2);
  
  % 设计4阶巴特沃斯带通滤波器
  [b_bandpass, a_bandpass] = butter(order, [low_normalized_bandpass high_normalized_bandpass], 'bandpass');
  disp('b_bandpass:');
  disp(b_bandpass);
  disp('a_bandpass:');
  disp(a_bandpass);
  

• Python代码

  '''使用Python获取带通滤波器系数'''
  from scipy.signal import butter, filtfilt
  fs = 250   # 采样率
  nyq = 0.5 * fs  # 归一化频率
  order = 4  # 阶数
  low_bandpass, high_bandpass = 4, 40
  Wn_bandpass = [low_bandpass / nyq, high_bandpass / nyq]
  b_bandpass, a_bandpass = butter(order, Wn_bandpass, btype='bandpass', analog=False)
  
  print("b_bandpass:", b_bandpass.tolist())
  print("a_bandpass:", a_bandpass.tolist())
  
  

2.2 数字滤波器差分函数

数字滤波器用于离散时间信号处理，即信号在离散时间点上采样并处理。差分方程是描述离散系统的一种标准数学形式，它使用输入、输出的当前和历史样本值，能很好地描述滤波器的递推关系。

一个典型的线性差分方程形式为：
$$y[n]=-\sum _{k=1}^N{a}_k\ast y[n-k]+\sum _{k=0}^M{b}_k\ast x[n-k]\text{\hspace{1em}(1)}$$

其中, $y[n]$是当前输出，$x[n]$是当前输入，$a_k$ 和 $b_k$ 是滤波器系数，$N$ 和 $M$ 分别是反馈和前馈的延迟阶数。

通过差分方程可以实现递归和非递归滤波器的结构：

• 非递归结构（FIR型滤波器）：仅包含输入的前馈项（即上式中的 $a_k=0$)，没有反馈项，因此更稳定，没有延迟累积或振荡问题。其数学形式为:
  $$y[n]=\sum _{k=0}^M{b}_k\ast x[n-k]\text{\hspace{1em}(2)}$$

• 递归结构（IIR型滤波器）：包含输出的反馈项，可以实现复杂的频率响应，但可能会导致非线性相位或稳定性问题。其数学形式为:
  $$y[n]=\sum _{k=0}^M{b}_k\ast x[n-k]-\sum _{k=1}^N{a}_k\ast y[n-k]\text{\hspace{1em}(3)}$$

由于IIR型滤波器具有低阶高效、计算量小、适合模拟滤波器特性以及良好的低频性能等优点，其在实时处理和资源受限的应用中具有显著优势。因此IIR型滤波器广泛用于音频处理、无线通信、航空航天、图像处理、医疗设备（ECG、EEG、超声信号处理）等领域。下面给出IIR型滤波器的差分函数C语言实现代码:

#include <stdio.h>
#include <math.h>
#include <memory.h>
#include <stdlib.h>
#include <string.h>
#define EPS 0.000001

// IIR型数字滤波器函数
void digitalFilter(const double* inputSignal, double* outputSignal, int inputLength, double* filterCoefficientsA, double* filterCoefficientsB, 
                   int filterLength, double* initialConditions) 
	{
	    double normalizationFactor;
	    int i, j;
	
	    // 判断是否需要归一化
	    if ((filterCoefficientsA[0] - 1.0 > EPS) || (filterCoefficientsA[0] - 1.0 < -EPS)) {
	        normalizationFactor = filterCoefficientsA[0];
	        for (i = 0; i < filterLength; i++) {
	            filterCoefficientsB[i] /= normalizationFactor;
	            filterCoefficientsA[i] /= normalizationFactor;
	        }
	    }
	
	    // 将输出信号初始化为零
	    for (i = 0; i < inputLength; i++) {
	        outputSignal[i] = 0.0;
	    }
	    
	    // 递归型差分方程
	    filterCoefficientsA[0] = 0.0;
    	for (i = 0; i < inputLength; i++) {
	        for (j = 0; i >= j && j < filterLength; j++) {
	            // 计算滤波器输出
	            outputSignal[i] += (filterCoefficientsB[j] * inputSignal[i - j] - filterCoefficientsA[j] * outputSignal[i - j]);
	        }
	        // 如果有初始条件且当前位置小于滤波器长度减一，加上初始条件
	        if (initialConditions && i < filterLength - 1) {
	            outputSignal[i] += initialConditions[i];
	        }
    }
    filterCoefficientsA[0] = 1.0;
}

2.3 滤波器的因果性与边缘效应

大多数滤波器都是因果滤波器，它们依赖当前和之前的样本来计算输出。当信号到达起点或终点时，缺少足够的历史或未来样本，导致滤波器无法正确初始化和延续滤波操作，从而产生不真实的波动或偏差。

滤波操作通常是卷积或相关操作的一种。在卷积运算中，滤波器窗口会滑动到信号的两端，而此时滤波器的一部分会超出信号范围。由于信号两端没有足够的数据来进行完整的卷积计算，这会导致滤波器输出不准确，产生边缘效应。

而在对任务态的EEG数据进行滤波处理时，我们希望滤波后的数据与滤波前的数据的相位保持一致，以避免出现相位偏移现象，影响事件相关电位分析、事件监测、伪影判别与脑网络分析等情况。零相位滤波信号器可成功克服这些不利因素，因为零相位滤波器在滤波后不会引起相位失真现象。而上述介绍的IIR型滤波器本身是因果的，会引入相位延迟，因此通常需要通过双向滤波来实现零相位响应。

双向滤波的原理是：由于正向滤波会带来一个正向的延迟，逆向滤波会带来一个逆向的延迟。因此先将信号先正向通过IIR滤波器，再反向通过同样的IIR滤波器，这样可以消除相位偏移。然而，这种双向滤波方式可能导致边界效应和稳定性问题。

2.4 矩阵乘法函数

为了实现稳定的双向滤波，通常使用状态空间模型来描述IIR滤波器。状态空间模型提供了矩阵表示的滤波器结构，可以方便地在正向和反向方向上进行递推，并且能够确保在双向滤波过程中保持系统的稳定性。

状态空间模型的形式为：
$$x[n+1]=Ax[n]+Bu[n]\text{\hspace{1em}(4)}$$
$$y[n]=Cx[n]+Du[n]\text{\hspace{1em}(5)}$$

这里，$A、B、C、D$ 是描述滤波器动态特性的矩阵。零相位滤波需要在正反方向上计算状态，这会涉及矩阵乘法和逆矩阵计算。为此，我们在实现零相位滤波器时应实现矩阵乘法与逆矩阵计算函数。

// 矩阵乘法函数
void matrixMultiplication(double* matrixA, double* matrixB, double* resultMatrix, int numRowsA, int numColsA, int numColsB) {
    int rowIndex, colIndex, commonIndex;
    int elementIndex;
    for (rowIndex = 0; rowIndex < numRowsA; rowIndex++) {
        for (colIndex = 0; colIndex < numColsB; colIndex++) {
            elementIndex = rowIndex * numColsB + colIndex;
            resultMatrix[elementIndex] = 0.0;
            // 遍历两个矩阵共同的维度，即矩阵A的列与矩阵B的行
            for (commonIndex = 0; commonIndex < numColsA; commonIndex++) {
                // 计算矩阵乘法
                resultMatrix[elementIndex] += matrixA[rowIndex * numColsA + commonIndex] * matrixB[commonIndex * numColsB + colIndex];
            }
        }
    }
    return;
}

2.5 逆矩阵函数

在双向滤波中，状态向量在滤波过程中反向运行。要实现这种反向递推（尤其是在状态空间模型中），需要求解状态向量的初始条件。这通常涉及到逆矩阵计算，特别是在确定系统的初始状态向量时，用于确保滤波结果的精确性和稳定性。

下面这个函数用于计算给定矩阵的逆矩阵。它使用高斯 - 约旦消元法来实现。首先，通过寻找最大元素来进行行和列的交换，以避免除以小的数导致数值不稳定。然后，逐步将矩阵转换为单位矩阵，同时对原始矩阵进行操作，最终得到逆矩阵。

int inverseMatrix(double* matrix, int matrixSize) {
    // 用于存储行和列的交换索引
    int* rowIndices, *columnIndices;
    int i, j, k, l, u, v;
    double d, p;

    // 分配内存
    rowIndices = (int*)malloc(matrixSize * sizeof(int));
    columnIndices = (int*)malloc(matrixSize * sizeof(int));

    for (k = 0; k < matrixSize; k++) {
        // 寻找最大元素
        d = 0.0;
        for (i = k; i < matrixSize; i++) {
            for (j = k; j < matrixSize; j++) {
                l = i * matrixSize + j;
                p = fabs(matrix[l]);
                if (p > d) {
                    d = p;
                    rowIndices[k] = i;
                    columnIndices[k] = j;
                }
            }
        }

        // 判断是否可逆
        if (d + 1.0 == 1.0) {
            free(rowIndices);
            free(columnIndices);
            printf("err**not invn");
            return 0;
        }

        // 交换行
        if (rowIndices[k]!= k) {
            for (j = 0; j < matrixSize; j++) {
                u = k * matrixSize + j;
                v = rowIndices[k] * matrixSize + j;
                p = matrix[u];
                matrix[u] = matrix[v];
                matrix[v] = p;
            }
        }

        // 交换列
        if (columnIndices[k]!= k) {
            for (i = 0; i < matrixSize; i++) {
                u = i * matrixSize + k;
                v = i * matrixSize + columnIndices[k];
                p = matrix[u];
                matrix[u] = matrix[v];
                matrix[v] = p;
            }
        }

        // 计算对角线元素的倒数
        l = k * matrixSize + k;
        matrix[l] = 1.0 / matrix[l];

        // 更新非对角线上的元素
        for (j = 0; j < matrixSize; j++) {
            if (j!= k) {
                u = k * matrixSize + j;
                matrix[u] = matrix[u] * matrix[l];
            }
        }

        for (i = 0; i < matrixSize; i++) {
            if (i!= k) {
                for (j = 0; j < matrixSize; j++) {
                    if (j!= k) {
                        u = i * matrixSize + j;
                        matrix[u] = matrix[u] - matrix[i * matrixSize + k] * matrix[k * matrixSize + j];
                    }
                }
            }
        }

        for (i = 0; i < matrixSize; i++) {
            if (i!= k) {
                u = i * matrixSize + k;
                matrix[u] = -matrix[u] * matrix[l];
            }
        }
    }

    // 恢复交换的列和行
    for (k = matrixSize - 1; k >= 0; k--) {
        if (columnIndices[k]!= k) {
            for (j = 0; j < matrixSize; j++) {
                u = k * matrixSize + j;
                v = columnIndices[k] * matrixSize + j;
                p = matrix[u];
                matrix[u] = matrix[v];
                matrix[v] = p;
            }
        }

        if (rowIndices[k]!= k) {
            for (i = 0; i < matrixSize; i++) {
                u = i * matrixSize + k;
                v = i * matrixSize + rowIndices[k];
                p = matrix[u];
                matrix[u] = matrix[v];
                matrix[v] = p;
            }
        }
    }

    // 释放内存
    free(rowIndices);
    free(columnIndices);
    return 0;
}

2.6 零相位滤波器函数

上面谈到零相位滤波器可成功消除相位失真的现象。这样的处理方式非常适合对时域特征要求严格的信号处理任务，如EEG信号分析，确保滤波后的信号在保留频率特征的同时，不会受到滤波器引入的相位延迟影响。

具体而言，本文借助于以下几个步骤，成功将IIR型滤波器转化为IIR型零相位型滤波器:

• 边缘反射扩展：为了减少滤波器对信号两端的边缘效应，可通过反射扩展输入信号的两端。前端和后端的信号样本被用来创建扩展信号，避免了因无法访问两端数据而产生的失真。

• 初始化滤波器状态：在IIR型滤波器中，初始条件对正确滤波非常关键。通过计算工作矩阵和瞬态向量，函数求解出初始条件，从而避免了滤波器启动时的瞬态响应对信号的影响。

• 正向滤波：对扩展信号执行正向滤波，得到初步的滤波结果。正向滤波会引入相位失真，但这不影响最终的结果，因为接下来会进行反向滤波。

• 反向滤波：反转正向滤波结果，并对反转后的信号执行逆向滤波。由于信号的顺序已经被反转，反向滤波能消除相位失真。

• 恢复原始顺序：反向滤波后的信号再反转回原始顺序，得到最终的零相位滤波结果。

• 内存管理：在整个过程中，动态分配了多个内存块用于存储扩展信号、滤波器状态、矩阵计算等中间结果，并在结束时释放内存，避免内存泄漏。

// filtfilt 函数：对输入信号进行零相位滤波
int filtfilt(double* input_signal, double* output_signal, int signal_length, double* filter_a, double* filter_b, int filter_order)
{
    int reflection_length;
    int extended_length;  // 扩展序列的长度，包括边缘反射部分
    int i;
    double *extended_signal, *filtered_signal, *p, *t, *end;
    double *workspace_matrix, *transient_vector, *initial_conditions;
    double first_sample, last_sample;

    // 根据滤波器阶数计算反射长度
    reflection_length = filter_order - 1;

    // 检查输入信号长度是否过短或滤波器参数是否无效
    if(signal_length <= 3 * reflection_length || filter_order < 2) return -1;

    // 定义扩展长度以容纳边缘反射，用于减小边缘效应
    extended_length = 6 * reflection_length + signal_length;
    extended_signal = (double *)malloc(extended_length * sizeof(double));
    filtered_signal = (double *)malloc(extended_length * sizeof(double));

    workspace_matrix = (double*)malloc(sizeof(double) * reflection_length * reflection_length);
    transient_vector = (double*)malloc(sizeof(double) * reflection_length);
    initial_conditions = (double*)malloc(sizeof(double) * reflection_length);

    // 检查内存分配是否成功
    if( !extended_signal || !filtered_signal || !workspace_matrix || !transient_vector || !initial_conditions ){
        free(extended_signal);
        free(filtered_signal);
        free(workspace_matrix);
        free(transient_vector);
        free(initial_conditions);
        return 1;
    }

    // 在信号开始处反射以减小边缘效应
    first_sample = input_signal[0];
    for(p = input_signal + 3 * reflection_length, t = extended_signal; p > input_signal; --p, ++t) 
        *t = 2.0 * first_sample - *p;

    // 复制信号的主体部分
    for(end = input_signal + signal_length; p < end; ++p, ++t) 
        *t = *p;

    // 在信号结束处反射以减小边缘效应
    last_sample = input_signal[signal_length - 1];
    for(end = extended_signal + extended_length, p -= 2; t < end; --p, ++t) 
        *t = 2.0 * last_sample - *p;

    // 初始化工作矩阵，用于求解初始条件
    memset(workspace_matrix, 0, sizeof(double) * reflection_length * reflection_length);

    workspace_matrix[0] = 1.0 + filter_a[1];
    for(i = 1; i < reflection_length; i++) {
        workspace_matrix[i * reflection_length] = filter_a[i + 1];
        workspace_matrix[i * reflection_length + i] = 1.0;
        workspace_matrix[(i - 1) * reflection_length + i] = -1.0;
    }

    // 计算用于初始条件的瞬态向量
    for(i = 0; i < reflection_length; i++) {
        transient_vector[i] = filter_b[i + 1] - filter_a[i + 1] * filter_b[0];
    }

    // 如果矩阵求逆成功，计算初始条件
    if(inverseMatrix(workspace_matrix, reflection_length)) {
        free(initial_conditions);
        initial_conditions = NULL;
    } else {
        matrixMultiplication(workspace_matrix, transient_vector, initial_conditions, reflection_length, reflection_length, 1);
    }

    free(workspace_matrix);
    free(transient_vector);

    // 对扩展信号执行正向滤波，将结果保存在 filtered_signal 中
    first_sample = extended_signal[0];
    if(initial_conditions) {
        for(p = initial_conditions, end = initial_conditions + reflection_length; p < end; ) 
            *(p++) *= first_sample;
    }
    digitalFilter(extended_signal, filtered_signal, extended_length, filter_a, filter_b, filter_order, initial_conditions);

    // 反转滤波后的信号以进行逆向滤波
    for(p = filtered_signal, end = filtered_signal + extended_length - 1; p < end; p++, end--) {
        double temp = *p;
        *p = *end;
        *end = temp;
    }

    // 对反转后的信号执行逆向滤波
    last_sample = (*filtered_signal) / first_sample;
    if(initial_conditions) {
        for(p = initial_conditions, end = initial_conditions + reflection_length; p < end; ) 
            *(p++) *= last_sample;
    }
    digitalFilter(filtered_signal, extended_signal, extended_length, filter_a, filter_b, filter_order, initial_conditions);

    // 将滤波后的信号反转回原顺序，并存储在 output_signal 中
    end = output_signal + signal_length;
    p = extended_signal + 3 * reflection_length + signal_length - 1;
    while(output_signal < end) {
        *output_signal++ = *p--;
    }

    // 清理分配的内存
    free(initial_conditions);
    free(extended_signal);
    free(filtered_signal);

    return 0;
}

3. 完整代码实现

#include <stdio.h>
#include <math.h>
#include <memory.h>
#include <stdlib.h>
#include <string.h>
#define EPS 0.000001

// IIR型数字滤波器函数
void digitalFilter(const double* inputSignal, double* outputSignal, int inputLength, double* filterCoefficientsA, double* filterCoefficientsB, 
                   int filterLength, double* initialConditions) 
	{
	    double normalizationFactor;
	    int i, j;
	
	    // 判断是否需要归一化
	    if ((filterCoefficientsA[0] - 1.0 > EPS) || (filterCoefficientsA[0] - 1.0 < -EPS)) {
	        normalizationFactor = filterCoefficientsA[0];
	        for (i = 0; i < filterLength; i++) {
	            filterCoefficientsB[i] /= normalizationFactor;
	            filterCoefficientsA[i] /= normalizationFactor;
	        }
	    }
	
	    // 将输出信号初始化为零
	    for (i = 0; i < inputLength; i++) {
	        outputSignal[i] = 0.0;
	    }
	    
	    // 递归式差分方程
	    filterCoefficientsA[0] = 0.0;
    	for (i = 0; i < inputLength; i++) {
	        for (j = 0; i >= j && j < filterLength; j++) {
	            // 计算滤波器输出
	            outputSignal[i] += (filterCoefficientsB[j] * inputSignal[i - j] - filterCoefficientsA[j] * outputSignal[i - j]);
	        }
	        // 如果有初始条件且当前位置小于滤波器长度减一，加上初始条件
	        if (initialConditions && i < filterLength - 1) {
	            outputSignal[i] += initialConditions[i];
	        }
    }
    filterCoefficientsA[0] = 1.0;
}



// 矩阵乘法函数
void matrixMultiplication(double* matrixA, double* matrixB, double* resultMatrix, int numRowsA, int numColsA, int numColsB) {
    int rowIndex, colIndex, commonIndex;
    int elementIndex;
    for (rowIndex = 0; rowIndex < numRowsA; rowIndex++) {
        for (colIndex = 0; colIndex < numColsB; colIndex++) {
            elementIndex = rowIndex * numColsB + colIndex;
            resultMatrix[elementIndex] = 0.0;
            // 遍历两个矩阵共同的维度，即矩阵A的列与矩阵B的行
            for (commonIndex = 0; commonIndex < numColsA; commonIndex++) {
                // 计算矩阵乘法
                resultMatrix[elementIndex] += matrixA[rowIndex * numColsA + commonIndex] * matrixB[commonIndex * numColsB + colIndex];
            }
        }
    }
    return;
}


//求逆矩阵，当返回值为0时成功求解逆矩阵
int inverseMatrix(double* matrix, int matrixSize) {
    // 用于存储行和列的交换索引
    int* rowIndices, *columnIndices;
    int i, j, k, l, u, v;
    double d, p;

    // 分配内存
    rowIndices = (int*)malloc(matrixSize * sizeof(int));
    columnIndices = (int*)malloc(matrixSize * sizeof(int));

    for (k = 0; k < matrixSize; k++) {
        // 寻找最大元素
        d = 0.0;
        for (i = k; i < matrixSize; i++) {
            for (j = k; j < matrixSize; j++) {
                l = i * matrixSize + j;
                p = fabs(matrix[l]);
                if (p > d) {
                    d = p;
                    rowIndices[k] = i;
                    columnIndices[k] = j;
                }
            }
        }

        // 判断是否可逆
        if (d + 1.0 == 1.0) {
            free(rowIndices);
            free(columnIndices);
            printf("err**not invn");
            return 0;
        }

        // 交换行
        if (rowIndices[k]!= k) {
            for (j = 0; j < matrixSize; j++) {
                u = k * matrixSize + j;
                v = rowIndices[k] * matrixSize + j;
                p = matrix[u];
                matrix[u] = matrix[v];
                matrix[v] = p;
            }
        }

        // 交换列
        if (columnIndices[k]!= k) {
            for (i = 0; i < matrixSize; i++) {
                u = i * matrixSize + k;
                v = i * matrixSize + columnIndices[k];
                p = matrix[u];
                matrix[u] = matrix[v];
                matrix[v] = p;
            }
        }

        // 计算对角线元素的倒数
        l = k * matrixSize + k;
        matrix[l] = 1.0 / matrix[l];

        // 更新非对角线上的元素
        for (j = 0; j < matrixSize; j++) {
            if (j!= k) {
                u = k * matrixSize + j;
                matrix[u] = matrix[u] * matrix[l];
            }
        }

        for (i = 0; i < matrixSize; i++) {
            if (i!= k) {
                for (j = 0; j < matrixSize; j++) {
                    if (j!= k) {
                        u = i * matrixSize + j;
                        matrix[u] = matrix[u] - matrix[i * matrixSize + k] * matrix[k * matrixSize + j];
                    }
                }
            }
        }

        for (i = 0; i < matrixSize; i++) {
            if (i!= k) {
                u = i * matrixSize + k;
                matrix[u] = -matrix[u] * matrix[l];
            }
        }
    }

    // 恢复交换的列和行
    for (k = matrixSize - 1; k >= 0; k--) {
        if (columnIndices[k]!= k) {
            for (j = 0; j < matrixSize; j++) {
                u = k * matrixSize + j;
                v = columnIndices[k] * matrixSize + j;
                p = matrix[u];
                matrix[u] = matrix[v];
                matrix[v] = p;
            }
        }

        if (rowIndices[k]!= k) {
            for (i = 0; i < matrixSize; i++) {
                u = i * matrixSize + k;
                v = i * matrixSize + rowIndices[k];
                p = matrix[u];
                matrix[u] = matrix[v];
                matrix[v] = p;
            }
        }
    }

    // 释放内存
    free(rowIndices);
    free(columnIndices);
    return 0;
}


// filtfilt 函数：对输入信号进行零相位滤波
int filtfilt(double* input_signal, double* output_signal, int signal_length, double* filter_a, double* filter_b, int filter_order)
{
    int reflection_length;
    int extended_length;  // 扩展序列的长度，包括边缘反射部分
    int i;
    double *extended_signal, *filtered_signal, *p, *t, *end;
    double *workspace_matrix, *transient_vector, *initial_conditions;
    double first_sample, last_sample;

    // 根据滤波器阶数计算反射长度
    reflection_length = filter_order - 1;

    // 检查输入信号长度是否过短或滤波器参数是否无效
    if(signal_length <= 3 * reflection_length || filter_order < 2) return -1;

    // 定义扩展长度以容纳边缘反射，用于减小边缘效应
    extended_length = 6 * reflection_length + signal_length;
    extended_signal = (double *)malloc(extended_length * sizeof(double));
    filtered_signal = (double *)malloc(extended_length * sizeof(double));

    workspace_matrix = (double*)malloc(sizeof(double) * reflection_length * reflection_length);
    transient_vector = (double*)malloc(sizeof(double) * reflection_length);
    initial_conditions = (double*)malloc(sizeof(double) * reflection_length);

    // 检查内存分配是否成功
    if( !extended_signal || !filtered_signal || !workspace_matrix || !transient_vector || !initial_conditions ){
        free(extended_signal);
        free(filtered_signal);
        free(workspace_matrix);
        free(transient_vector);
        free(initial_conditions);
        return 1;
    }

    // 在信号开始处反射以减小边缘效应
    first_sample = input_signal[0];
    for(p = input_signal + 3 * reflection_length, t = extended_signal; p > input_signal; --p, ++t) 
        *t = 2.0 * first_sample - *p;

    // 复制信号的主体部分
    for(end = input_signal + signal_length; p < end; ++p, ++t) 
        *t = *p;

    // 在信号结束处反射以减小边缘效应
    last_sample = input_signal[signal_length - 1];
    for(end = extended_signal + extended_length, p -= 2; t < end; --p, ++t) 
        *t = 2.0 * last_sample - *p;

    // 初始化工作矩阵，用于求解初始条件
    memset(workspace_matrix, 0, sizeof(double) * reflection_length * reflection_length);

    workspace_matrix[0] = 1.0 + filter_a[1];
    for(i = 1; i < reflection_length; i++) {
        workspace_matrix[i * reflection_length] = filter_a[i + 1];
        workspace_matrix[i * reflection_length + i] = 1.0;
        workspace_matrix[(i - 1) * reflection_length + i] = -1.0;
    }

    // 计算用于初始条件的瞬态向量
    for(i = 0; i < reflection_length; i++) {
        transient_vector[i] = filter_b[i + 1] - filter_a[i + 1] * filter_b[0];
    }

    // 如果矩阵求逆成功，计算初始条件
    if(inverseMatrix(workspace_matrix, reflection_length)) {
        free(initial_conditions);
        initial_conditions = NULL;
    } else {
        matrixMultiplication(workspace_matrix, transient_vector, initial_conditions, reflection_length, reflection_length, 1);
    }

    free(workspace_matrix);
    free(transient_vector);

    // 对扩展信号执行正向滤波，将结果保存在 filtered_signal 中
    first_sample = extended_signal[0];
    if(initial_conditions) {
        for(p = initial_conditions, end = initial_conditions + reflection_length; p < end; ) 
            *(p++) *= first_sample;
    }
    digitalFilter(extended_signal, filtered_signal, extended_length, filter_a, filter_b, filter_order, initial_conditions);

    // 反转滤波后的信号以进行逆向滤波
    for(p = filtered_signal, end = filtered_signal + extended_length - 1; p < end; p++, end--) {
        double temp = *p;
        *p = *end;
        *end = temp;
    }

    // 对反转后的信号执行逆向滤波
    last_sample = (*filtered_signal) / first_sample;
    if(initial_conditions) {
        for(p = initial_conditions, end = initial_conditions + reflection_length; p < end; ) 
            *(p++) *= last_sample;
    }
    digitalFilter(filtered_signal, extended_signal, extended_length, filter_a, filter_b, filter_order, initial_conditions);

    // 将滤波后的信号反转回原顺序，并存储在 output_signal 中
    end = output_signal + signal_length;
    p = extended_signal + 3 * reflection_length + signal_length - 1;
    while(output_signal < end) {
        *output_signal++ = *p--;
    }

    // 清理分配的内存
    free(initial_conditions);
    free(extended_signal);
    free(filtered_signal);

    return 0;
}



int main()
{
	// 例子带通滤波器系数（4阶Butterworth带通滤波器，采样率250Hz， 4-40Hz）
    double b_bandpass[] = {0.016255176549541173, 0.0, -0.06502070619816469, 0.0, 
	                       0.09753105929724704, 0.0, -0.06502070619816469, 0.0, 0.016255176549541173};
    double a_bandpass[] = {1.0, -5.360703285534569, 12.74230451194405, -17.736407401314917, 
	                       15.949378473690096, -9.51256976782561, 3.6615254094399727, -0.8286427351763588, 0.08515392332605591};
	
	// 定义测试的待滤波数据, 1s, 250个采样点
	double x[] = {7994.9079,  7978.61475, 7976.6703,  7992.0918,  8006.7534,  8000.07075,  7987.5771,  7984.0458,  7999.9143,  8014.4418,
                  8004.0714,  7983.04005, 7980.8721,  7994.70675, 8009.0778,  7999.93665,  7981.4979,  7978.3242,  7994.66205, 8007.84855, 
				  7997.2323,  7981.6767,  7984.2693,  7999.9143,  8012.7879,  8001.18825,  7982.8389,  7984.06815, 7998.19335, 8004.8313,
                  7994.7291,  7978.9053,  7976.24565, 7989.52155, 7999.75785, 7988.31465,  7978.12305, 7977.2514,  7993.49985, 8009.10015, 
				  7997.74635, 7978.57005, 7973.4519,  7987.24185, 8006.28405, 7999.13205,  7983.88935, 7980.2463,  7992.38235, 8005.8147,
				  7998.7074,  7981.43085, 7977.2514,  7991.8236,  8008.07205, 7997.12055,  7980.0675,  7974.10005, 7985.36445, 7998.37215, 
				  7990.0803,  7974.8376,  7971.55215, 7982.45895, 7999.8249,  7995.2655,   7977.81015, 7978.7712,  7995.3549,  8004.9207, 
				  7990.8849,  7975.21755, 7977.00555, 7994.03625, 8008.0497,  7997.1429,   7979.86635, 7978.25715, 7996.40535, 8008.69785, 
				  7998.23805, 7983.26355, 7982.2131,  7996.89705, 8008.74255, 7999.0203,   7981.20735, 7978.7265,  7996.13715, 8013.3243, 
				  8005.39005, 7987.51005, 7984.91745, 7999.2438,  8010.7764,  8000.2272,   7989.11925, 7989.2757,  7999.44495, 8006.46285, 
				  7996.36065, 7982.8836,  7979.37465, 7998.8415,  8017.01205, 8006.59695,  7990.5273,  7983.5541,  7999.71315, 8015.2017, 
				  8008.7202,  7992.96345, 7991.48835, 8006.9769,  8018.1966,  8004.89835,  7983.2859,  7979.77695, 8002.1046,  8017.86135, 
				  8005.6806,  7985.9232,  7985.40915, 8005.47945, 8017.0791,  8003.8926,   7986.34785, 7990.90725, 8005.5465,  8017.99545, 
				  8011.2681,  7991.1531,  7988.09115, 8005.3677,  8016.498,   8003.95965,  7989.0522,  7995.6231,  8011.7598,  8022.86775, 
				  8014.6653,  7997.3664,  7995.3996,  8011.02225, 8022.6666,  8008.69785,  7988.80635, 7987.9794,  7998.86385, 8011.3128, 
				  8001.5682,  7987.3983,  7986.07965, 8000.07075, 8011.4022,  8003.8479,   7993.05285, 7994.2821,  8009.54715, 8023.203, 
				  8014.1736,  7996.8747,  7992.69525, 8005.5912,  8019.3588,  8009.1225,   7998.0369,  7999.6014,  8014.06185, 8020.4316, 
				  8011.37985, 8000.3166,  8000.8083,  8017.68255, 8027.226,   8007.98265,  7995.33255, 7997.52285, 8016.34155, 8029.2375, 
				  8016.52035, 7997.2323,  7993.7457,  8009.81535, 8020.72215, 8006.73105,  7994.84085, 7995.64545, 8007.0216,  8012.1621, 
				  7999.6908,  7987.28655, 7987.19715, 8001.6576,  8012.45265, 7997.96985,  7986.83955, 7987.51005, 8001.4341,  8010.03885,
				  7993.2093,  7978.5924,  7979.2629,  7995.8019,  8003.3562,  7993.72335,  7980.00045, 7979.91105, 7998.68505, 8014.1289, 
				  8000.0931,  7983.57645, 7982.05665, 7996.36065, 8008.8543,  8000.51775,  7983.93405, 7982.50365, 7997.47815, 8011.0446, 
				  8000.1378,  7981.0956,  7980.5592,  7998.1263,  8010.97755, 8001.4341,   7989.3204,  7989.07455, 7998.7074,  8007.53565, 
				  7995.91365, 7984.7163,  7984.91745, 8004.9207,  8015.13465, 8003.51265,  7987.2642,  7985.2080,  8007.4239,  8019.3588, 
				  8005.83705, 7994.61735, 7995.46665, 8006.5299,  8014.50885, 8001.41175,  7984.51515, 7983.5541,  8001.6576,  8009.9718};
	
    
    // 使用自定义的滤波器对250个采样点数据进行数字滤波
    int x_length = 250;
    double y[250];
    
    int coeff_length = sizeof(b_bandpass) / sizeof(b_bandpass[0]);

    // 应用filtfilt进行带通滤波
    filtfilt(x, y, x_length, a_bandpass, b_bandpass, coeff_length);
    
    // 打开文件进行写入
    FILE *output_file = fopen("c_output_signal_blog.txt", "w");
    
    if (output_file == NULL) {
        printf("Failed to open file for writing!\n");
        return 1;
    }
    
    // 输出结果
    printf("Output result after bandpass filtering in C language:\n");
    for (int i = 0; i < x_length; i++) {
        printf("%f, ", y[i]);
        // 打开文件进行写入
        fprintf(output_file, "%f\n", y[i]);
    }
    
    return 0;
}

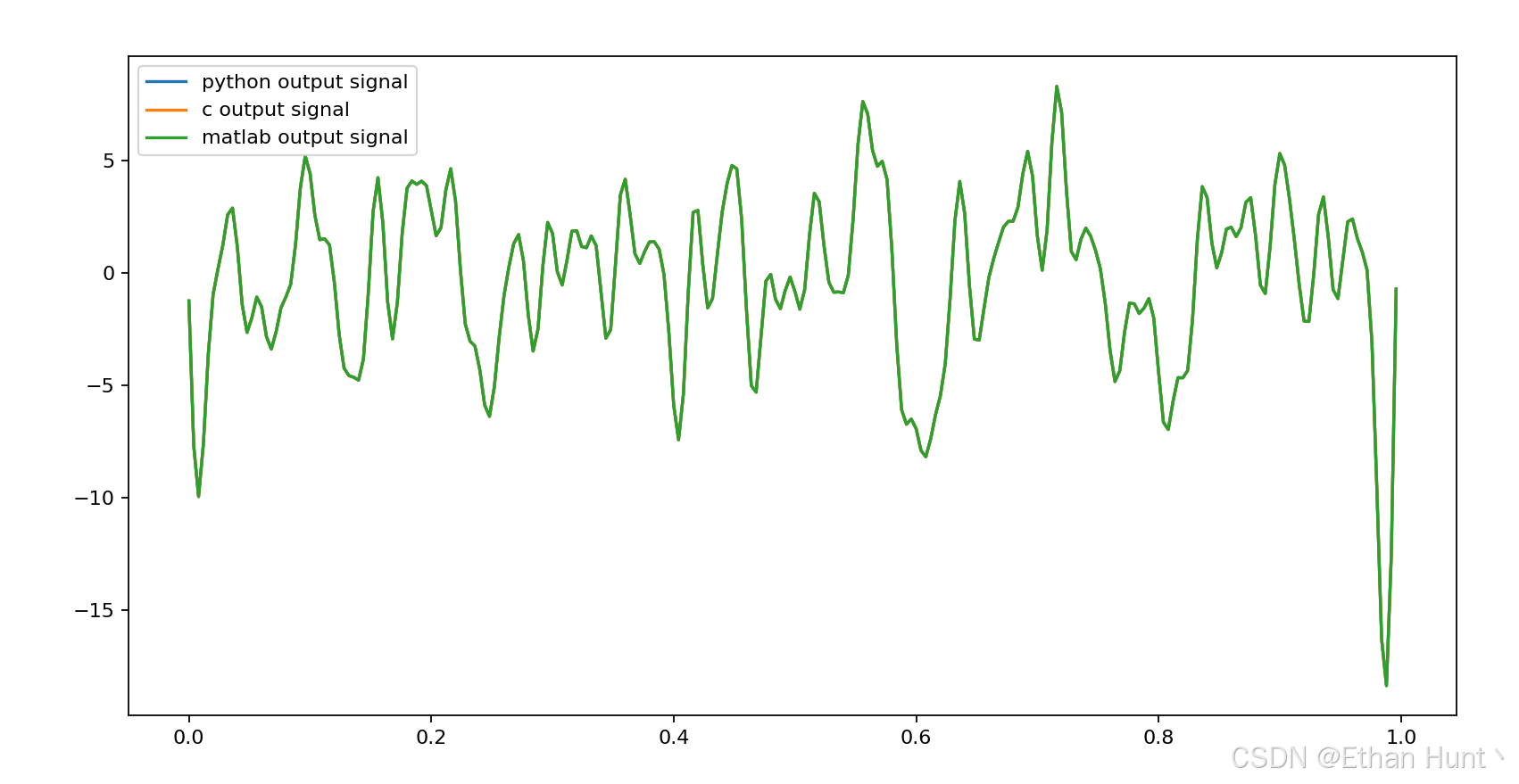
4. 实现效果对比

当使用相同的滤波系数与输入信号时，python、c、matlab三种编程语言实现的零相位IIR型滤波器输出信号在绘图时曲线应完全重合，如下图所示: