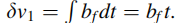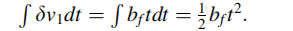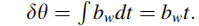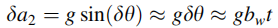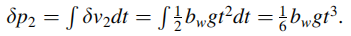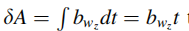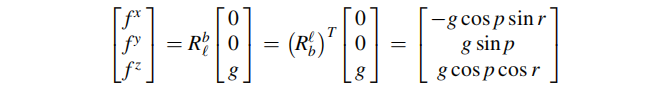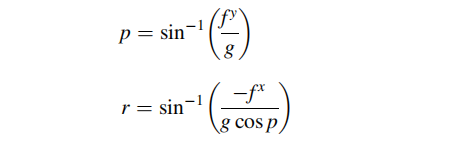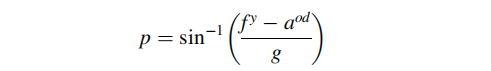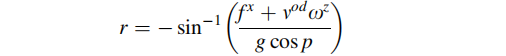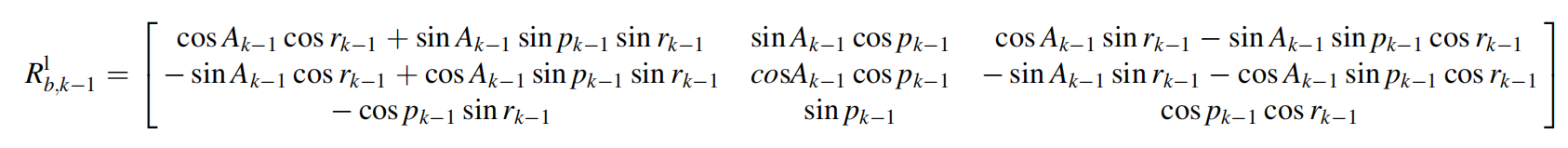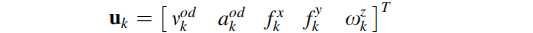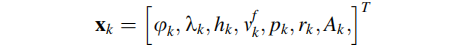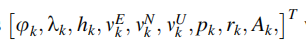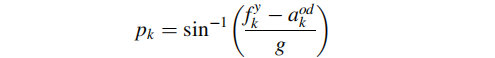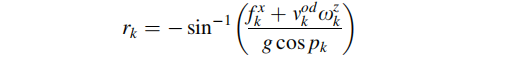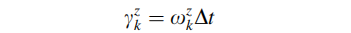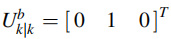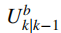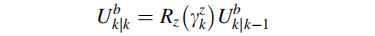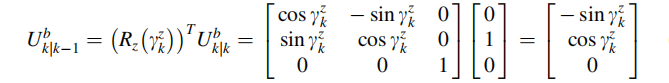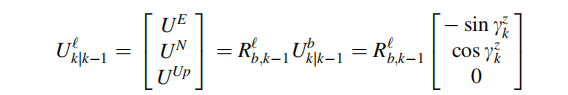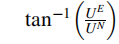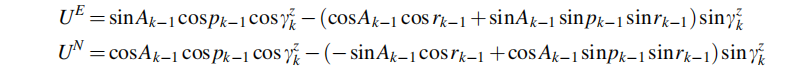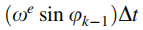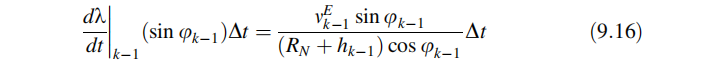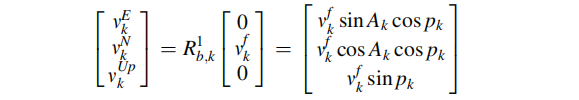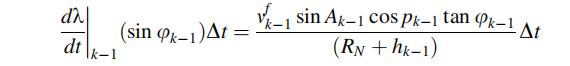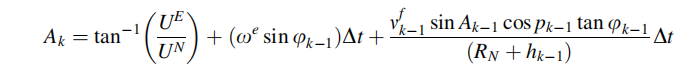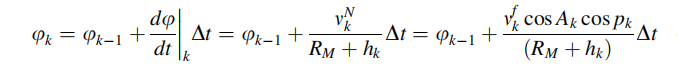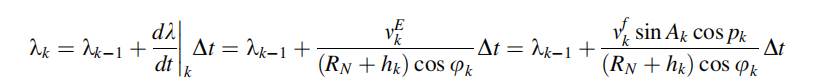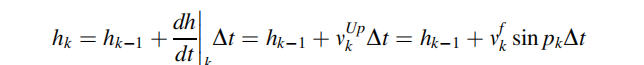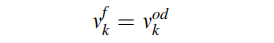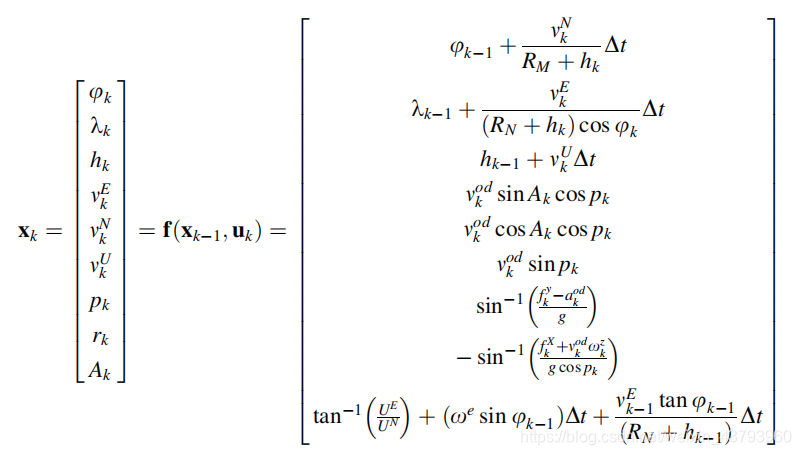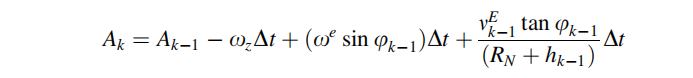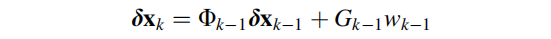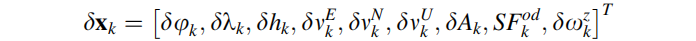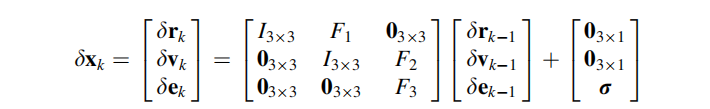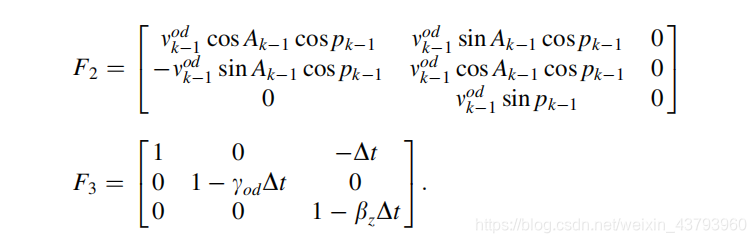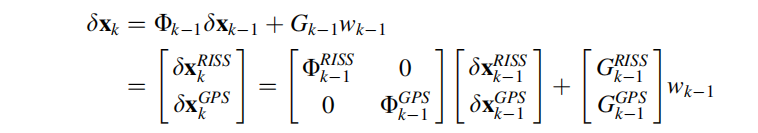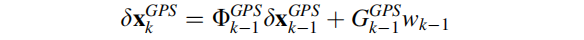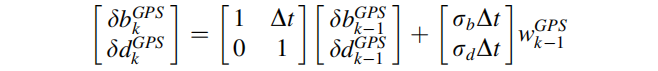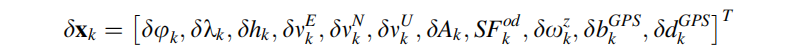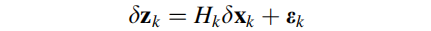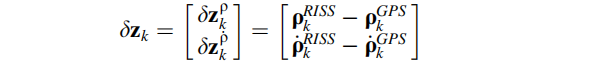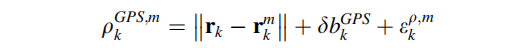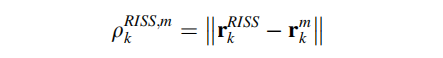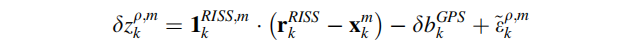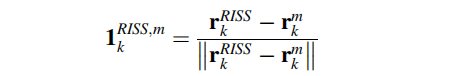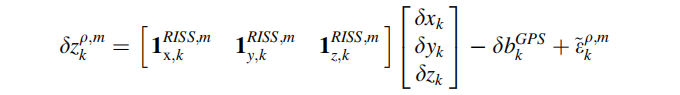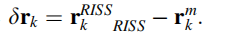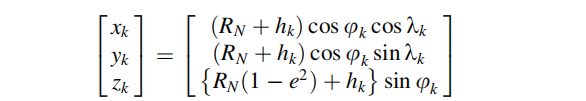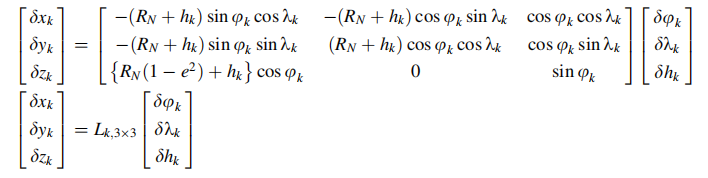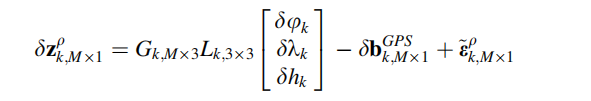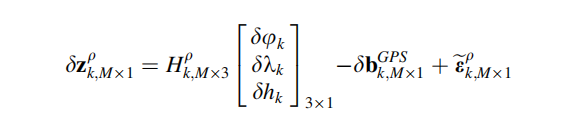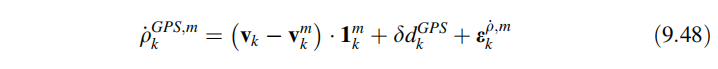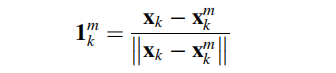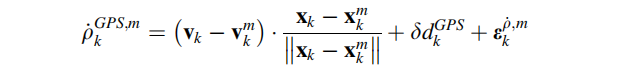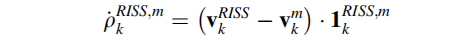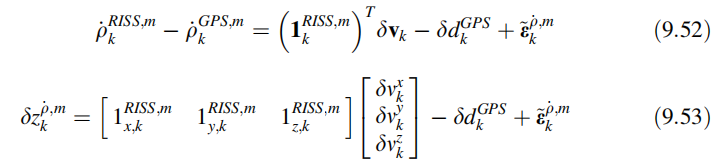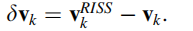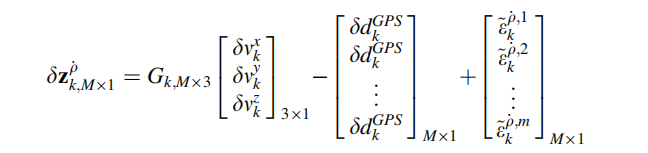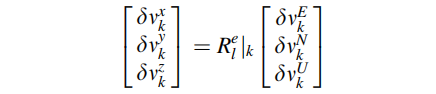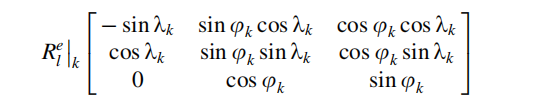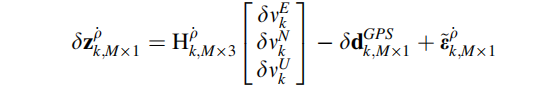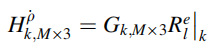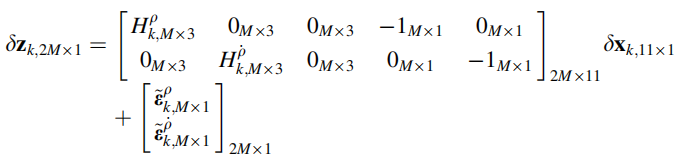简化INS与GPS组合系统在三维路面上的导航
这一章节讨论一种适用于任何轮式平台(含GPS)的航迹推算(DR)方法,该方法可消除使用传统IMU尤其是低精度IMU时产生的一些误差。
1.首先分析讨论一个完整的INS系统,再概述用于处理误差源的理论方法。
2.介绍了一种简化的惯性传感器系统,并与传统IMU进行比较。推导简化INS的机械化方程。
3.接着,描述基于KF 的松耦合和紧耦合的简化惯性传感器系统与GPS的集成,包括线性化的系统模型和各种组合方案的测量模型。
1 MEMS级IMU的三维定位的性能分析
在GPS拒止的情况下,以低精度MEMS级IMU作为惯性传感器进行三维导航,三种未经补偿的bais如下:三个加速度计中未经补偿的bias;水平对齐的陀螺仪未经补偿的bias;竖直对齐的陀螺仪未经补偿的bias。
正如第7章讨论的,LKF和EKF都试图通过传感器的误差模型对这些偏差进行补偿。在GPS可用时,误差模型间接得到更新。在GPS中断时KF滤波以预测模式运行,并从机械化解中减去INS误差的预测值进行修正。但这种补偿是不完善的,仍然存在一些未补偿的剩余误差。
下面将讨论这些未补偿偏差的影响。
第一个误差源,(第四章提到)当通过加速度计算位置与速度时,未经补偿的加速度偏差 bf 将会产生以下影响:
1 速度误差与时间 t成正比 (GPS拒止时,KF工作在预测模式下)
2 位置误差与 t 的平方成正比
第二个误差源,两个水平方向的陀螺仪之间存在一个未经补偿的偏差 bw :
1 俯仰角或横摇角的误差与时间成正比
这一小角度误差会造成INS无法正确对齐。当加速度从 b 系投影到 L系时,由于这一偏差的存在,会导致加速度矢量的投影产生误差。
2 加速度在水平方向上的误差(L系)
在GPS拒止期间,deta(theta)为一个很小的角,通过近似 sin(deta theta)== data theta
3 偏差 bw将导致速度误差以及位置误差
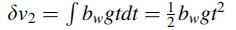
由上式,陀螺仪误差在位置上产生了三阶误差。当INS单独工作时,这些陀螺仪误差将是位置和速度误差中最具影响力的部分。
误差的第三个来源:是由于垂直方向上未补偿的陀螺仪误差bw,会引起方位角的误差。
同样,该方位角误差与时间成正比。
2 解决MEMS级IMU在路面导航中存在的问题
land-based vehicle :陆地车辆场景
这一小节主要概述适用于(带有里程计或轮式编码器)陆地车辆的导航方法。通过一些方法来消除低精度IMU带来的未经补偿的误差,使得惯性传感器的成本最小化。
为了解决上一节中提到的第一个误差(由加速度计偏差引起),可以将里程计的速度用到导航解算中。
为了克服第二个误差(水平陀螺仪偏差),俯仰角与横滚角将综合加速度计与里程计的测量值得到。
以下给出pitch角与roll角的简要推导方程:
当车辆静止时,若俯仰和滚转轴所在平面与水平面之间存在倾斜,则加速度计测量可以在这两个轴上测量到重力分量。加速度计的测量值为:
因为上式只使用了沿着 X 和 Y 方向的两个加速度计使,则,俯仰角和横摇角可以表示为:
当车辆移动时,前向加速度计( y )(已修正传感器误差)测量车辆前向加速度以及重力分量。为了计算俯仰角,前向加速度计测量值必须减去里程计测量得的车辆加速度:
其中,g为重力加速度,fy为前向加速度计测量值,aod为里程计测量的车辆加速度。
与之类似,横向加速度( x )包含了车辆加速度的垂直分量以及重力分量。为了计算roll角,必须对加速度的垂直分量进行补偿:
其中,fx为横向加速度测量值,vod为里程计测得的速度,wz为z轴上的陀螺仪测得的角速率。vod 与wz相乘即为车辆加速的垂直分量。
对于低精度的MEMS IMU来说,通过两个加速度计来计算pitch和roll角 通常比使用两个陀螺仪在计算具有更大优势。
原因1: 使用两个水平陀螺仪计算俯仰和横摇,涉及到积分操作,而使用加速度计算则不需要。积分的缺点在于,未经补偿的传感器误差通过积分累积,造成定位精度的不断下降。
原因2: 陀螺仪与加速度计相比,加速计更便宜
原因3: 垂直方向的陀螺仪的偏差需要用到组合导航的滤波器进行建模。
3 三维简化的惯性传感器系统
为了降低陆地车辆导航方案的成本,提出了一种简化的惯性传感器导航(reduced inertial sensor system,简称RISS)方法用于二维环境导航,其中采用单轴陀螺仪与里程作为传感器并通过kalman滤波与GPS集成。这种二维 RISS/GPS方法,需要假设车辆在水平面上移动。之所以被称为RISS,是因为它还包含一对用于计算俯仰角和横滚角的加速度计。
一个单一的陀螺仪,其敏感轴与车辆的天向轴对齐。假定车辆在水平面上行驶,它的速度通过里程计的测量值计算得到,并与陀螺仪获得的航向信息一起使用,以确定东、北两个方向的速度,继而可以计算经度与纬度。这种简化的多传感器系统为2D路面导航提供了一个有效地方案。
如前文中提到的,若要确定俯仰角和滚转角,可以使用两个额外的加速度计。这两个加速度计一个指向车辆的正前方,一个指向横向,再根据地球重力矢量以及速度测量模型,就可以计算出横滚与俯仰的角度。这些角度的计算是为了确定载体平面与水平面的关系,并不包含在KF的动态建模中。
3.1 3D RISS概述
此处主要讨论三维RISS解决方案,由两个用于计算俯仰和横摇的 加速度计 提供测量值被合并到一起以估计偏离水平面的运动,这种方法可以作为三维环境下的导航方案。
事实证明,与完整的惯性传感器相比(完整的IMU包含了三个加速度计和三个陀螺仪),在陆地车辆上使用一个前向加速度计和三个陀螺仪的传感器配置,同样也能够进行导航参数的求解,计算出三维的位置、速度以及姿态。
这也意味着三个陀螺仪加上从车辆里程计中获得的前向速度就足以实现三维导航。
这一节介绍使用车辆的里程计、一个单轴陀螺仪和两个加速度计来实现三维导航方案。
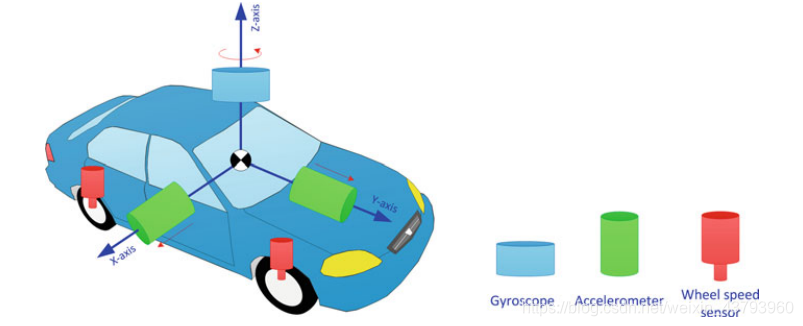
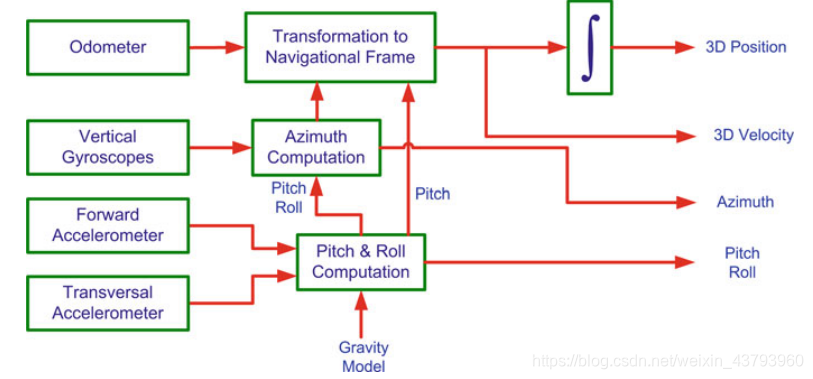
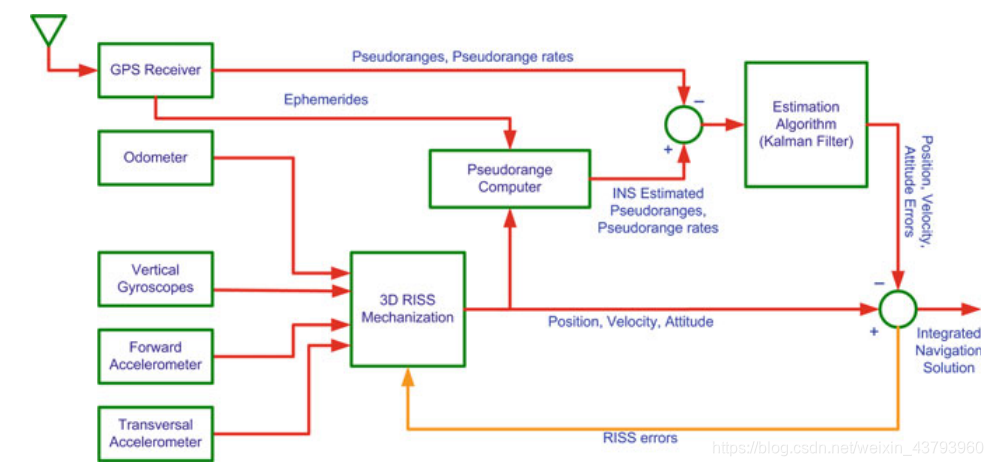
陀螺仪与车辆的垂直轴对齐,原本用于计算俯仰与横摇的两个陀螺仪在这里使用两个加速度计进行替代。三维RISS集成了垂直方向的陀螺仪和两个水平加速度计的测量数据,速度读数由里程表或车轮编码器提供,三维RISS系统如图所示:
利用三维RISS系统可获得三维位置、三维速度和三维姿态的导航解。
3.2 (轮式车辆)采用3D RISS系统的优点
三维RISS相对于二维航位推算的优点在于,使用两个加速度计的测量值 计算偏离水平面的运动。
优点1:可以计算出正确的方位角。由于陀螺仪(与车身框架垂直对齐)在不完全水平状态下是倾斜的,因此无法测量水平E-N平面的角速度。由于方位角在E-N平面上,因此相比于2D车辆航迹推算时忽略水平面因素的做法,3D RISS方法通过检测和校正陀螺仪倾斜可以计算出一个更为精确的方位角。
优点2:可以得到比2D RISS更精确的2D水平定位。 原因有二: (1)结合俯仰角和里程表中的速度可以计算出两个更为精确的水平速度,因此能够提供更好的位置估计; (2)方位角计算越精确,东向和北向的速度估计就越准确,继而得到更精确的位置。
优点3:3D RISS 相比2D车辆航迹推算的优点在于可以计算出 向上的速度以及海拔高度。
与传统IMU相比,3D RISS的优点是通过加速计来计算俯仰角和横滚角而非陀螺仪,在计算速度上使用了里程计而非加速度计。
那么,为什么使用加速度计来计算角度比使用陀螺仪更好呢?优越性体现在哪里?
解释:未经补偿的水平陀螺仪bias,会引起俯仰与横滚的角度误差,这一误差由于进行积分计算与时间成正比,会导致加速度矢量从boay系到 L系统的投影过程产生误差,引入一个加速度误差之后,后续计算的速度与 t2成正比,位置与 t3成正比。
若是通过加速度计来计算俯仰和横滚角,可免去一次积分计算,并且角度误差不与时间t成比例。此外,角度误差引起的速度和位置误差也可以下降一个阶次。
除了上述优点,RISS在速度计算上进一步优化。使用里程计来计算速度与使用加速度计计算速度相比,可以获得更好性能。
解释:使用加速度计计算速度时,任何未经补偿的加速度误差都会引入一个与t成正比的速度误差以及与t2成正比的位置误差。在长期无法获得GPS信号的情况下,使用加速度计计算速度造成的误差随中断时间不断增大,这对导航计算来说是十分不利的。
而使用里程计的测量值来计算速度可以避免一次积分计算,这意味只要进行一次积分就能够得到位置。
在3D RISS中,唯一剩下的主要误差源就是 垂直对齐的陀螺引起的方位角误差,陀螺仪未经补偿的bias会导致方位角误差并与时间成正比。方位角引起的位置误差将正比于车速、时间以及方位角误差。这些误差必须在积分滤波器内通过模拟陀螺仪的随机漂移来解决。
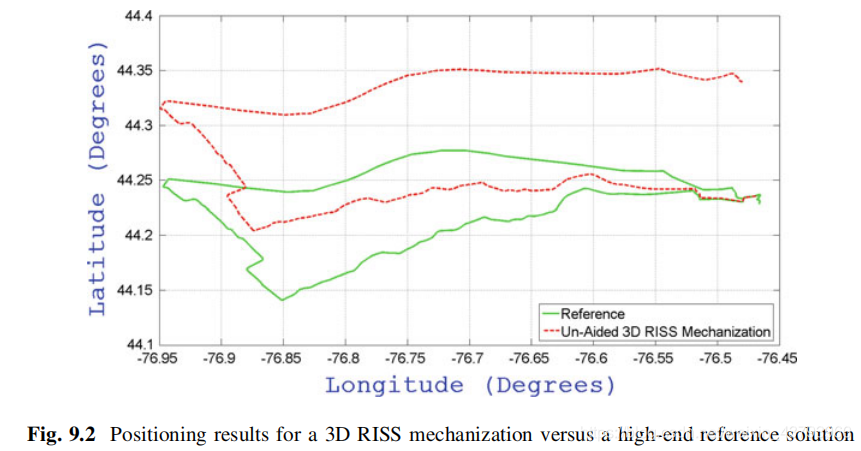
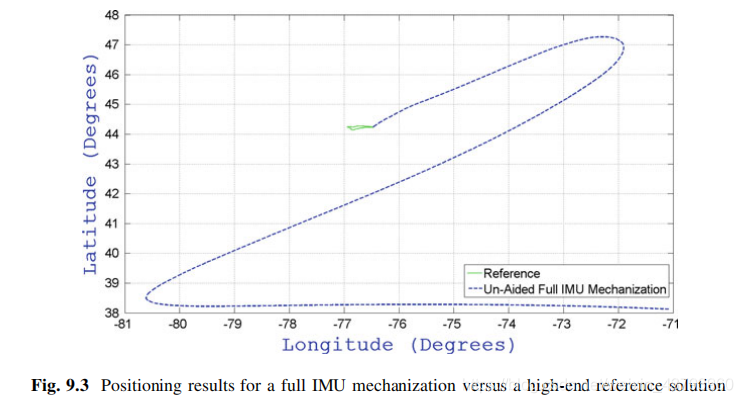
为了证明3D RISS比完整的IMU传感器在陆地车辆导航上更具优势,以下分别将两种导航方法用于路面汽车行驶的导航中,在约96公里的轨道上运行,持续时间约100分钟,得到两者的位置输出,两个系统的定位结果见图:
图9.2为使用3D RISS系统得到的位置轨迹与高精度参考轨迹的对比。
图9.3为使用IMU传感器估计的位置轨迹与高精度参考轨迹的对比。从图中可以看出,随着时间推移,Full IMU轨迹很快出现了漂移,并偏离真实轨迹。
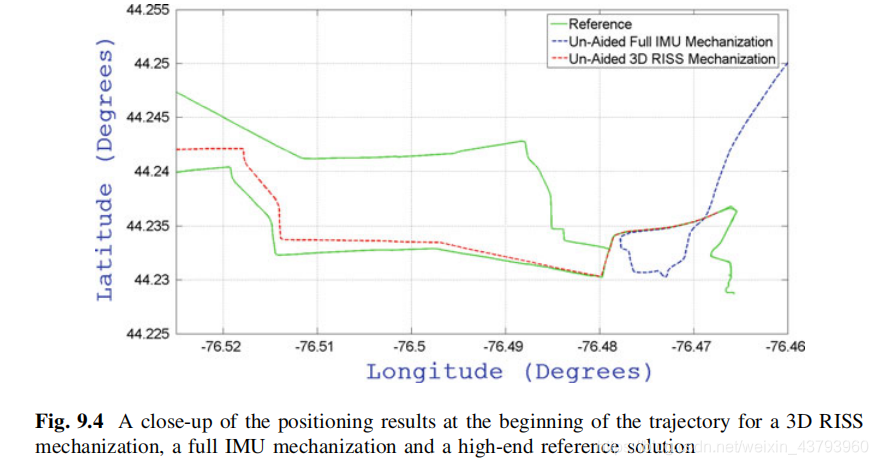
图9.4为运动起始位置的局部图,此处展示了使用full IMU更容易产生漂移。其中,3D RISS与full IMU中使用的MEMS传感器来自于相同的IMU(IMU300CC-100型),该IMU的陀螺仪bias为2°/s。
3.3 3D RISS的运动方程推导
本节给出了包含位置、速度和姿态状的三维RISS的非线性运动模型。
使用通用的参考系,b系的x轴与车体的横向重合,y轴与车体的前向重合z轴沿着车体垂直向上的方向。局部坐标系(L系)是沿东、北、天方向的ENU坐标系。在k-1时刻时,旋转矩阵从车载体坐标旋转到局部坐标系为:
为了描述运动模型,首先需要控制输入。由一个陀螺仪、两个加速计和里程计提供的传感器测量值组成了控制输入向量:
定义系统的导航状态为:
此处状态向量只包含了前向速度,在有些方程中采用
将东、北、天的速度都作为状态向量。
3.3.1 Pitch和roll角的计算
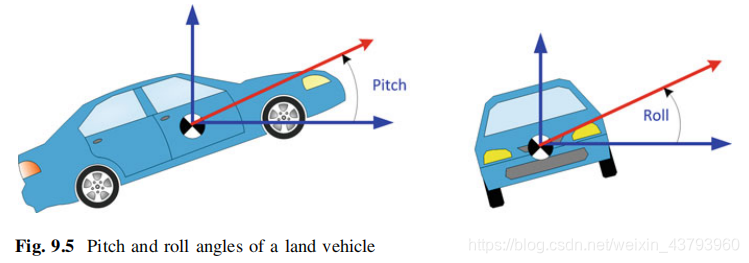
对于陆地车辆来说,俯仰角是相对于水平地面的角度(即绕横向轴的旋转),横滚角是绕纵向轴的旋转,如图所示:
当车辆运动时,前向加速度计测量车辆的前向加速度以及重力分量。为了计算俯仰角,需要在前向加速度的测量值中减去里程计测得的车辆加速度:
同样的,横向加速度计测量车辆的横向加速度以及重力分量。为了计算roll角,必须对横向加速度进行补偿:
3.3.2 航向角计算
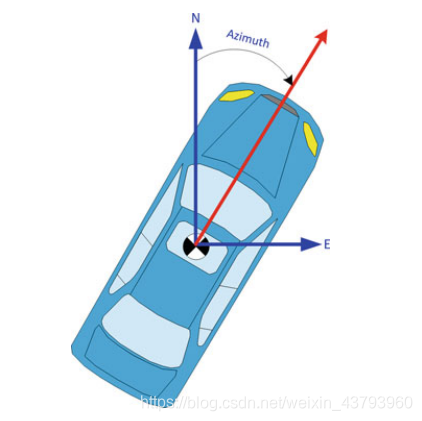
陆地车辆的方位角实际为车辆正前方朝向与大地北向的夹角,如图所示:
在k-1与k的时间间隔内,绕载体b系的z轴逆时针旋转,得到:
计算目标:求得方位角在E-N平面上的投影。
在k时刻获得车辆b系下的前向单位矢量:
假设在已知k-1时刻的车辆状态,对k时刻的车辆前向单位矢量进行估计:
从k-1时刻的车辆载体坐标系到k时刻载体坐标系之间的旋转矩阵是Rz,那么两个单位矢量的关系可以看成:
由于Rz是一个正交的旋转矩阵,因此:
(注:正交矩阵性质:ATA=E 、AT=A’)
由式可得,k时刻沿车辆前进方向的单位矢量,可由k-1时刻的车辆在 L系下的前向单位矢量得到:
因此,由于绕z轴的旋转产生的新的航向角为:
其中:
使用上式定义的航向角,是相对于北向的夹角,沿顺时针方向为正。
除了表现为车辆的旋转之外,方位角还有两个额外的分量。这是由于地球自转以及L系方向变化引起的。
··由于地球自转引起的分量为:
We为地球旋转速率,这一部分可以直接在新的航向角上进行补偿。
··由于L坐标系相对于地球坐标系的方向变化引起的分量为(沿逆时针方向):
由于,车辆的body系与local-level系之间的关系为:
代入(9.16)式,得到:
在计算方位角时需要加上这一项。
综上,得到最终的方位角计算模型为:
3.3.3 三维位置、速度计算
注:【非完整约束】非完整约束与完整约束的区别
至少包含一个不可积微分约束的动力系统称非完整系统。对非完整系统,要用更复杂的微分方程来描述。带有滚动轮子的系统(如自行车、汽车、飞机起落架等)大都是非完整系统。位置约束为完整约束,速度约束为非完整约束。
由于陆地车辆的非完整约束(non-holonomic constraint),车身body系中的速度仅由车辆前向(纵向)速度构成,水平横向以及垂直向的速度分量均为0。
因此,纬度可以表示为:
其中,RM为地球曲率半径,deta( t)为采样时间。
同理,经度可以表示为:
海拔高度表示为:
其中,车辆前向速度为:
3.4 3D RISS 运动模型概述
完整的运动模型如下:
如果在导航状态矢量中使用是L系中的速度分量,而非前向速度,那么运动模型将变为:
三维RISS模型如图所示:
4 KF用于松耦合的3D RISS/GPS集成
非线性运动模型构成了机械化方程的基础,由此推导出的线性化误差状态模型,可作为kalman滤波的系统模型。
为了简化线性化系统模型,并将其作为3D RISS的误差模型,这里做了两个近似:第一个近似,将俯仰和横滚角的误差作为状态量排除在积分滤波器之外。(正如前面所讨论的,俯仰和横滚的误差不随时间增长)第二个近似,假设陀螺仪(沿着车身b系的垂直向上方向)与位置L系的天向对齐,简化了方位角的计算。(由于这个陀螺仪的测量包含了地球自转的分量以及局地坐标系在地球系上的旋转,所以在积分之前这些量被从测量中除去。)
基于上述方位角的二维近似,可以将L系中的方位角直接表示为:
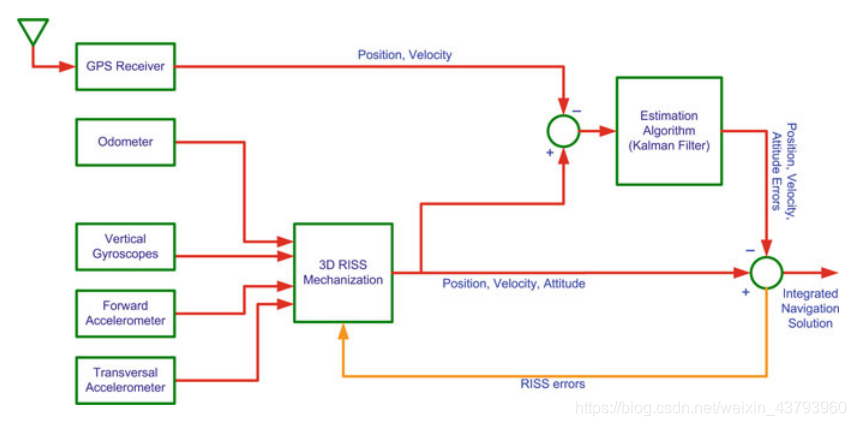
松耦合的3D RISS/GPS集成的系统框图如下所示:
4.1 3D RISS的线性化误差模型
3D RISS KF的误差状态系统模型可表示为:
kalman滤波器的误差状态矢量为:
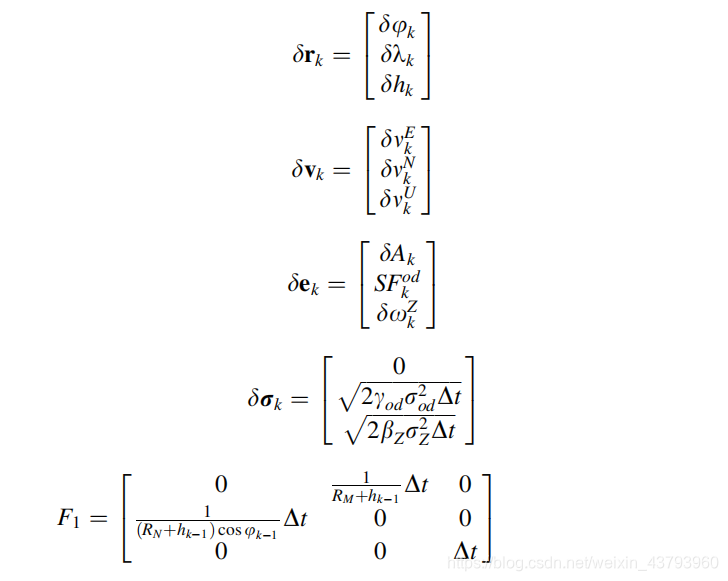
其中:
如先秦所述,运动模型时非线性的,因此必须对其进行线性化才能得到可作为KF系统模型的误差模型。
通过泰勒级数展开并忽略高阶项,将方程线性化。
得到对应的线性化误差状态系统模型为:
其中:
陀螺仪的随机误差以及里程计得到的速度,都采用高斯-马尔科夫模型。
4.2 用于更新3D RISS的测量模型
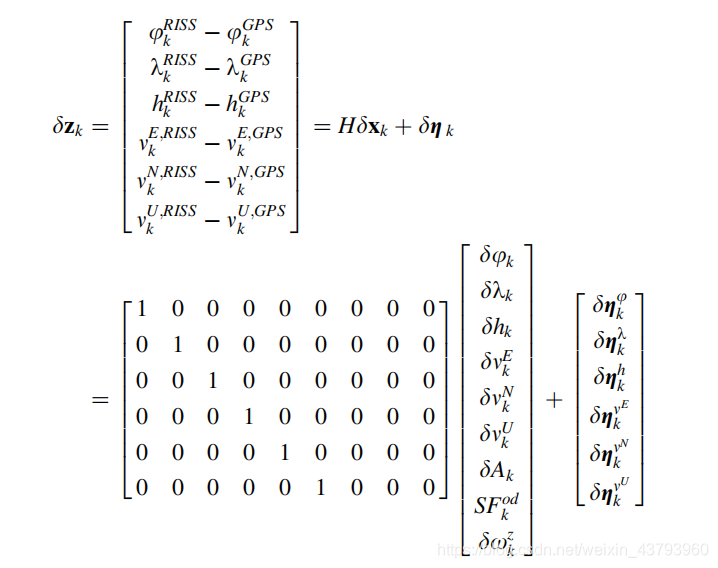
由于考虑的是松耦合集成,所以在KF的更新阶段使用了GPS的位置和速度进行更新,滤波器使用的测量模型为:(测量模型为RISS提供的3D位置、速度与GPS测量值的差值)
5 KF用于紧耦合的3D RISS/GPS集成
紧耦合的3D RISS/GPS集成系统框图,如下所示:
5.1 系统模型的扩维
紧耦合的系统模型与松耦合类似,在系统模型和状态矢量都包含了GPS接收机的时钟偏差以及漂移误差。因此RISS和GPS可以简单地结合在一起,得到以下完整的系统模型为:
kalman滤波系统模型中的GPS方程为:
GPS接收器的时钟偏差和它的漂移被包含在状态中,这些状态的系统模型是:
因此,扩维后的状态矢量为:
5.2 用于更新3D RISS的原始GPS测量模型
给出紧耦合的KF线性化测量模型:
GPS的观测值是伪距以及伪距速率。因此,对于KF的误差状态来说,测量矢量由 RISS 与 GPS的伪距测量值以及伪距速率测量值的差值构成:
在第三章中提到过,GPS的测量值经过了时钟误差以及电离层和对流层的校正。对于M个可接受信号的卫星,以上方程可写为:
这些非线性伪距误差来自于伪距测量值以及RISS计算的位置预测出的伪距值。
因此,第M颗卫星与GPS之间的伪距可由以下模型表示:
由RISS导航系统输出的预测伪距 定义为:
其中,r(RISS,K)为车辆位置,由ECEF大地坐标系转换到ECEF直角坐标系,再由机械化方程计算位置输出得到。
GPS伪距测量值与车辆位置无关,但对最新估计状态进行泰勒展开之后,使得RISS估计值与GPS测量值之间的差异可以被建模为与位置误差线性相关的式子:
以分量形式表示:
其中:
在获得M个卫星的测量之后,可以得到:
其中:
由于状态矢量的位置分量在大地坐标系中,因此需要将其转化到对应的直角坐标系上:
上式的线性化位置误差为:
将上式带入到(9.42)式中,得到:
通过定义一个H矩阵,线性化的伪距测量模型为:
通过测量卫星载频的多普勒频移,计算了第m颗卫星的伪距离速率测量值。如第3章所述,伪距离速率可视为接收器和卫星之间的相对速度测量,测量的方向是从卫星指向接收器方向的单位矢量,测量模型可以用数学形式表示:
在(9.48)中:
因此,可重写为:
通过RISS估计伪距速速率为:
其中 v(RISS,k)为通过RISS估计的ECEF直角坐标系下的车辆速度。
因此,线性化的伪距速率测量方程如下:
其中:
对M个可接收信号的卫星,伪距速率测量可以写为:
速度在局部水平坐标系(L)与ECEF坐标系之间的关系为:
将坐标系转换代入测量方程,得到伪距速率测量模型:
其中:
综上,得到包含伪距以及伪距速率的完整的测量模型为: