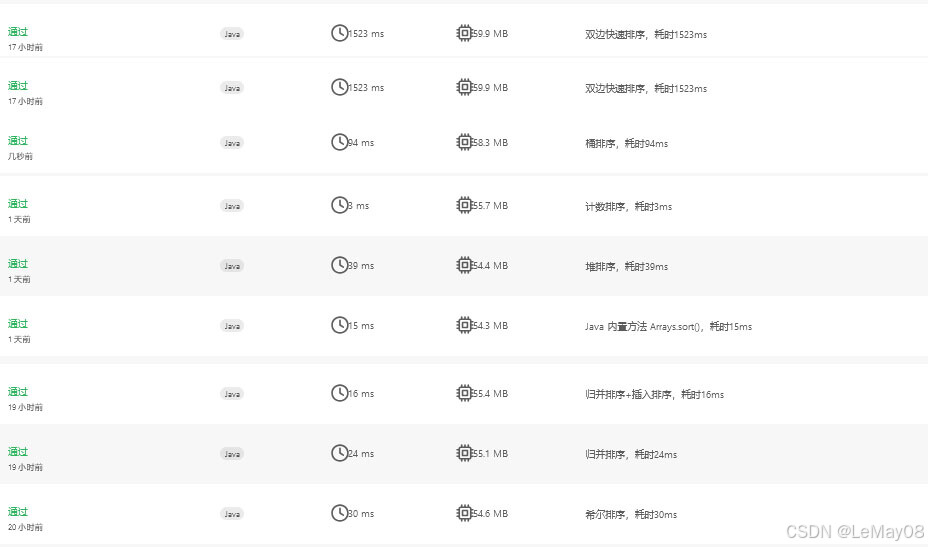
1.概述
比较排序算法
| 算法 | 最好 | 最坏 | 平均 | 空间 | 稳定 | 思想 | 注意事项 |
|---|---|---|---|---|---|---|---|
| 冒泡 | O(n) | O( n 2 n^2 n2) | O( n 2 n^2 n2) | O(1) | Y | 比较 | 最好情况需要额外判断 |
| 选择 | O( n 2 n^2 n2) | O( n 2 n^2 n2) | O( n 2 n^2 n2) | O(1) | N | 比较 | 交换次数一般少于冒泡 |
| 堆 | O( n l o g n nlogn nlogn) | O( n l o g n nlogn nlogn) | O( n l o g n nlogn nlogn) | O(1) | N | 选择 | 堆排序的辅助性较强,理解前先理解堆的数据结构 |
| 插入 | O(n) | O( n 2 n^2 n2) | O( n 2 n^2 n2) | O(1) | Y | 比较 | 插入排序对于近乎有序的数据处理速度比较快,复杂度有所下降,可以提前结束 |
| 希尔 | O(nlogn) | O( n 2 n^2 n2) | O( n l o g n nlogn nlogn) | O(1) | N | 插入 | gap序列的构造有多种方式,不同方式处理的数据复杂度可能不同 |
| 归并 | O( n l o g n nlogn nlogn) | O( n l o g n nlogn nlogn) | O( n l o g n nlogn nlogn) | O(n) | Y | 分治 | 需要额外的O(n)的存储空间 |
| 快速 | O( n l o g n nlogn nlogn) | O( n 2 n^2 n2) | O( n l o g n nlogn nlogn) | O(logn) | N | 分治 | 快排可能存在最坏情况,需要把枢轴值选取得尽量随机化来缓解最坏情况下的时间复杂度 |
非比较排序算法
| 非比较排序算法 | 时间复杂度 | 空间复杂度 | 稳定性 |
|---|---|---|---|
| 计数排序 | O(n+k) | O(n+k) | 稳定 |
| 桶排序 | O(n+k) | O(n+k) | 稳定 |
| 基数排序 | O(d*(n+k)) | O(n+k) | 稳定 |
其中
- n 是数组长度
- k 是桶长度
- d 是基数位数
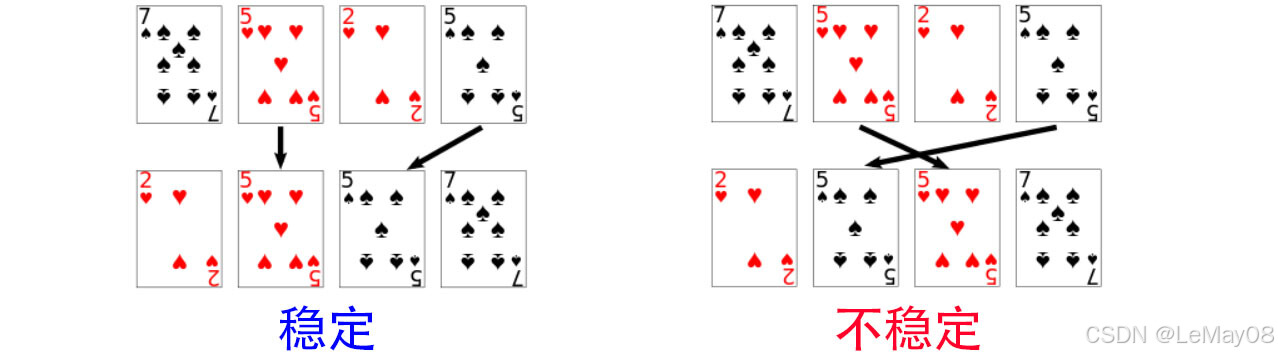
稳定 vs 不稳定
说明:两个相同的数排序后没有发生改变,说明是稳定的
2.冒泡排序
- 每轮冒泡不断地比较相邻的两个元素,如果它们是逆序的,则交换它们的位置
- 下一轮冒泡,可以调整未排序的右边界,减少不必要比较
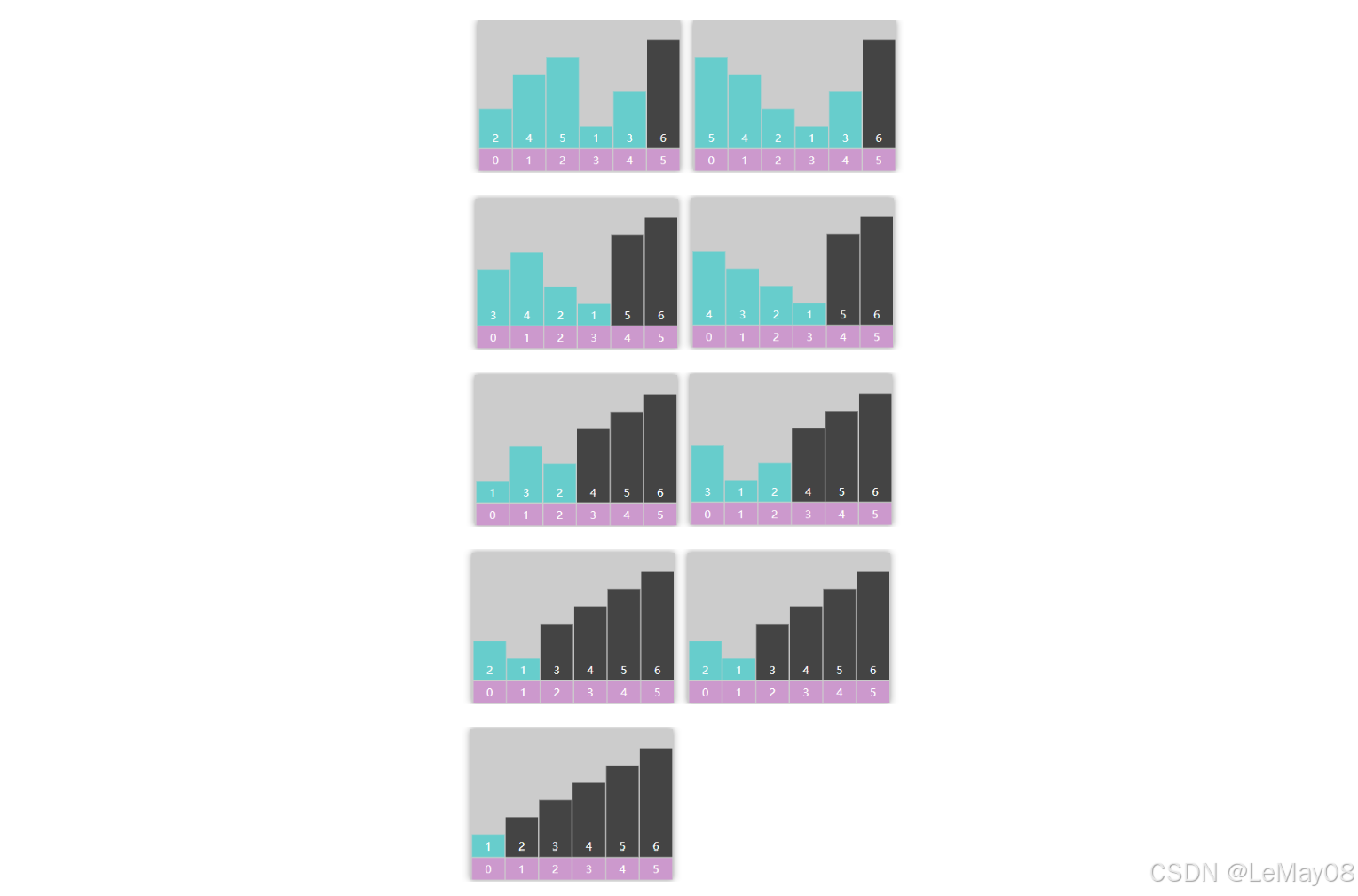
以数组 3、2、1 的冒泡排序为例,第一轮冒泡
第二轮冒泡
未排序区域内就剩一个元素,结束
public void bubbleSort(int[] nums) {
for (int i = 0; i < nums.length - 1; i++) {
for (int j = 0; j < nums.length - 1 - i; j++) {
if (nums[j] > nums[j + 1]) {
int temp = nums[j];
nums[j] = nums[j + 1];
nums[j + 1] = temp;
}
}
}
}
优化手段:每次循环时,若能确定更合适的右边界,则可以减少冒泡轮数
以数组 3、2、1、4、5 为例,第一轮结束后记录的 x,即为右边界
public void bubbleSort(int[] nums) {
int j = nums.length - 1;
while (true) {
int x = 0;
for (int i = 0; i < j; i++) {
if (nums[i] > nums[i + 1]) {
int temp = nums[i];
nums[i] = nums[i + 1];
nums[i + 1] = temp;
x = i;
}
}
j = x;
if (j == 0) {
break;
}
}
}
3.选择排序
- 每一轮选择,找出最大(最小)的元素,并把它交换到合适的位置
以下面的数组选择最大值为例
public void selectSort(int[] nums) {
for (int i = 0; i < nums.length - 1; i++) {
for (int j = i + 1; j < nums.length; j++) {
if (nums[i] > nums[j]) {
int temp = nums[i];
nums[i] = nums[j];
nums[j] = temp;
}
}
}
}
4.堆排序
- 建立大顶堆
- 每次将堆顶元素(最大值)交换到末尾,调整堆顶元素,让它重新符合大顶堆特性
建堆
交换,下潜调整
public class HeapSort {
public static void main(String[] args) {
int[] nums = new int[]{3, 2, 1, 4, 5, 7, 9, 6, 8};
new HeapSort().heapSort(nums);
System.out.println(Arrays.toString(nums));
}
//堆排序
public void heapSort(int[] nums) {
//1.建堆操作,符合大顶堆的特性
heapify(nums, nums.length);
//2.每次将堆顶元素(最大值)交换到末尾,调整堆顶元素,让它重新符合大顶堆特性
for (int i = nums.length - 1; i > 0; i--) {
swap(nums, 0, i);
down(nums, 0, i);//交换完了以后不符合大顶堆的特性
}
}
//建堆
private void heapify(int[] nums, int size) {
//从倒数第一个非叶子节点开始以此下潜
int start = (size - 2) / 2;//非叶子节点的索引
for (int i = start; i >= 0; i--) {
down(nums, i, size);
}
}
//下潜
private void down(int[] nums, int parent, int size) {
/**
* 方式一:递归实现
*/
/*int left = 2 * parent + 1;
int right = 2 * parent + 2;
int max = parent;
if (left < size && nums[left] > nums[max]) {
max = left;
}
if (right < size && nums[right] > nums[max]) {
max = right;
}
if (parent != max) {
swap(nums, parent, max);
down(nums, max, size);
}*/
/**
* 方式二:循环实现
*/
while (true) {
int left = 2 * parent + 1;
int right = 2 * parent + 2;
int max = parent;
if (left < size && nums[left] > nums[max]) {
max = left;
}
if (right < size && nums[right] > nums[max]) {
max = right;
}
if (parent == max) {
break;
}
swap(nums, parent, max);
parent = max;
}
}
//交换
private void swap(int[] nums, int i, int j) {
int temp = nums[i];
nums[i] = nums[j];
nums[j] = temp;
}
}
5.插入排序
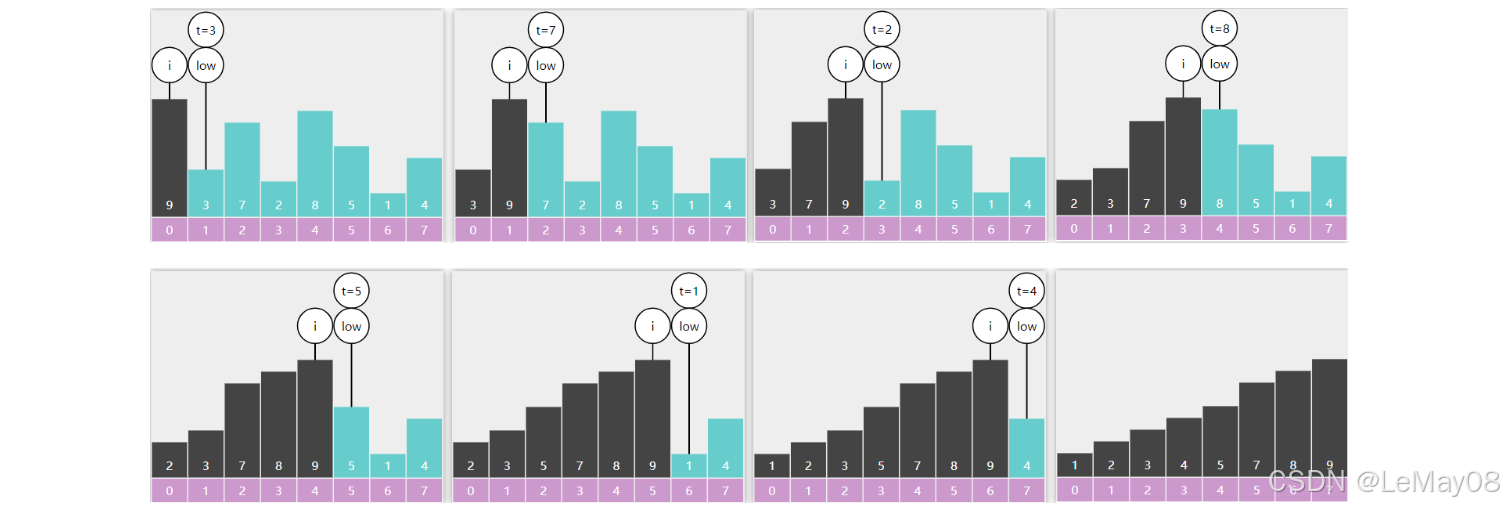
- 将数组分为两部分 [0 … low-1] [low … a.length-1]
- 左边 [0 … low-1] 是已排序部分
- 右边 [low … a.length-1] 是未排序部分
- 每次从未排序区域取出 low 位置的元素, 插入到已排序区域
递归版
public void insertSort(int[] nums) {
sort(nums, 1);
}
private void sort(int[] nums, int low) {
if (low == nums.length) {
return;
}
int t = nums[low];
int i = low - 1;
while (i >= 0 && t < nums[i]) {
nums[i + 1] = nums[i];
i--;
}
if (i != low - 1) {
nums[i + 1] = t;
}
sort(nums, low + 1);
}
非递归版
public void insertSort(int[] nums) {
for (int low = 1; low < nums.length; low++) {
int t = nums[low];
int i = low - 1;
while (i >= 0 && t < nums[i]) {
nums[i + 1] = nums[i];
i--;
}
if (i != low - 1) {
nums[i + 1] = t;
}
}
}
6.希尔排序
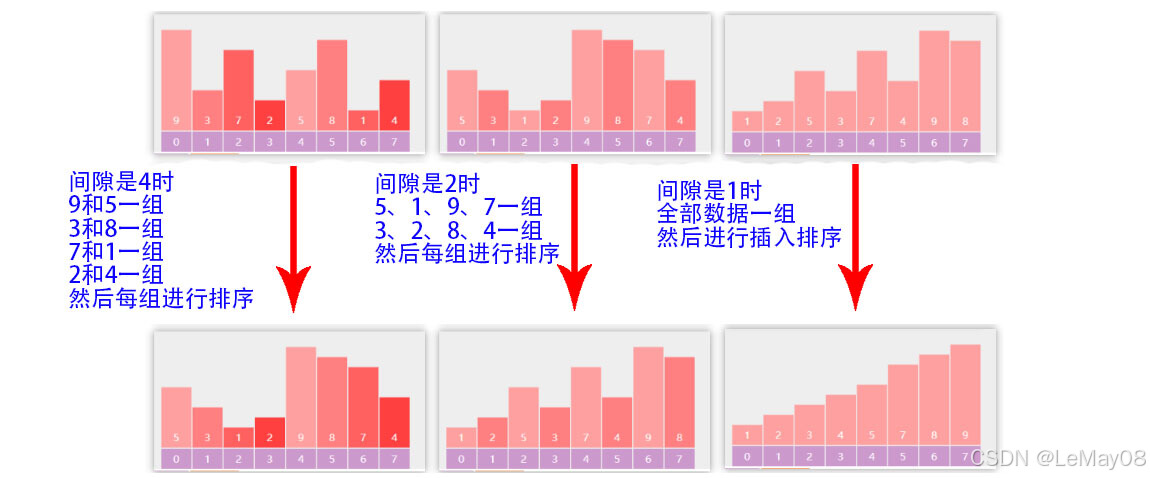
- 简单的说,就是分组实现插入,每组元素间隙称为 gap
- 每轮排序后 gap 逐渐变小,直至 gap 为 1 完成排序
- 对插入排序的优化,让元素更快速地交换到最终位置
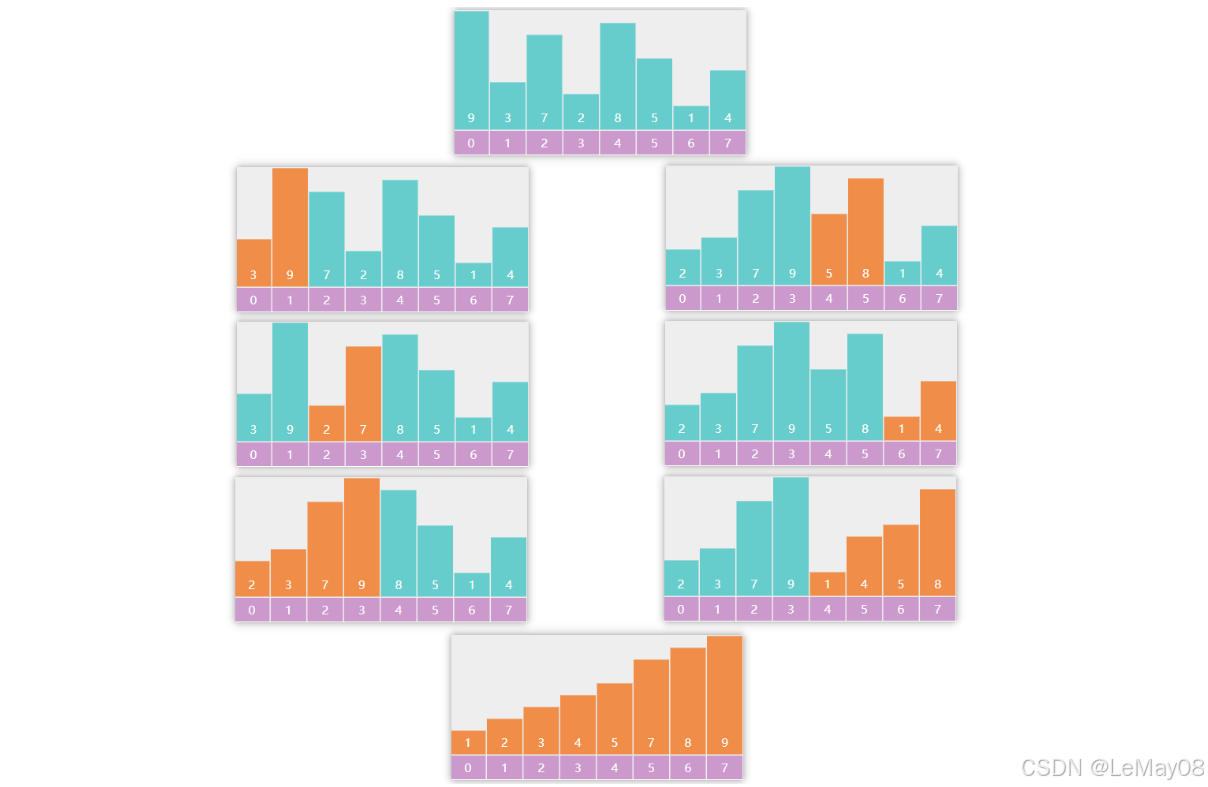
下图演示了 gap = 4,gap = 2,gap = 1 的三轮排序前后比较
public void shellSort(int[] nums) {
for (int gap = nums.length >> 1; gap >= 1; gap = gap >> 1) {
//原插入排序
for (int low = gap; low < nums.length; low++) {
int t = nums[low];
int i = low - gap;
while (i >= 0 && t < nums[i]) {
nums[i + gap] = nums[i];
i -= gap;
}
if (i != low - gap) {
nums[i + gap] = t;
}
}
}
}
7.归并排序
- 分 - 每次从中间切一刀,处理的数据少一半
- 治 - 当数据仅剩一个时可以认为有序
- 合 - 两个有序的结果,可以进行合并排序
递归实现
public class MergeSort {
public static void main(String[] args) {
int[] nums = new int[]{3, 2, 1, 4, 5, 7, 9, 6, 8, 0};
new MergeSort().mergeSort(nums);
System.out.println(Arrays.toString(nums));
}
private void mergeSort(int[] nums) {
int[] merge = new int[nums.length];
split(nums, merge, 0, nums.length - 1);
}
//对数组进行切分
private void split(int[] nums, int[] merge, int left, int right) {
if (left == right) {//不可再切了
return;
}
//寻找中间点,以中间点进行切分
int mid = (left + right) >>> 1;
//切分
split(nums, merge, left, mid);
split(nums, merge, mid + 1, right);
merge(nums, merge, left, mid, mid + 1, right);
System.arraycopy(merge, left, nums, left, right - left + 1);
}
/**
* 合并两个有序数组
*
* @param array 原始数组
* @param merge 合并后的数组
* @param i 第一个有序范围的起始位置
* @param iEnd 第一个有序范围的结束位置
* @param j 第二个有序范围的起始位置
* @param jEnd 第二个有序范围的结束位置
*/
private void merge(int[] array, int[] merge, int i, int iEnd, int j, int jEnd) {
int k = i;
while (i <= iEnd && j <= jEnd) {
if (array[i] < array[j]) {
merge[k] = array[i];
i++;
} else {
merge[k] = array[j];
j++;
}
k++;
}
if (i > iEnd) {
System.arraycopy(array, j, merge, k, jEnd - j + 1);
}
if (j > jEnd) {
System.arraycopy(array, i, merge, k, iEnd - i + 1);
}
}
}
非递归实现
public class MergeSort {
public static void main(String[] args) {
int[] nums = new int[]{3, 2, 1, 4, 5, 7, 9, 6, 8, 0};
new MergeSort().mergeSort(nums);
System.out.println(Arrays.toString(nums));
}
private void mergeSort(int[] nums) {
int length = nums.length;
int[] merge = new int[length];
//width代表有序区间的宽度,取值是1,2,4,8
for (int width = 1; width < length; width *= 2) {
//[left,right]代表待合并区间的左右边界
for (int left = 0; left < length; left += 2 * width) {
int right = Integer.min(2 * width + left - 1, length - 1);
int mid = Integer.min(left + width - 1, length - 1);
merge(nums, merge, left, mid, mid + 1, right);
}
//合并数组
System.arraycopy(merge, 0, nums, 0, length);
}
}
/**
* 合并两个有序数组
*
* @param array 原始数组
* @param merge 合并后的数组
* @param i 第一个有序范围的起始位置
* @param iEnd 第一个有序范围的结束位置
* @param j 第二个有序范围的起始位置
* @param jEnd 第二个有序范围的结束位置
*/
private void merge(int[] array, int[] merge, int i, int iEnd, int j, int jEnd) {
int k = i;
while (i <= iEnd && j <= jEnd) {
if (array[i] < array[j]) {
merge[k] = array[i];
i++;
} else {
merge[k] = array[j];
j++;
}
k++;
}
if (i > iEnd) {
System.arraycopy(array, j, merge, k, jEnd - j + 1);
}
if (j > jEnd) {
System.arraycopy(array, i, merge, k, iEnd - i + 1);
}
}
}
归并排序 + 插入排序
- 小数据量且有序度高时,插入排序效果高
- 大数据量用归并效果好
- 可以结合二者
public class MergeInsertSort {
public static void main(String[] args) {
int[] nums = new int[]{3, 2, 1, 4, 5, 7, 9, 6, 8, 0};
new MergeInsertSort().mergeSort(nums);
System.out.println(Arrays.toString(nums));
}
private void mergeSort(int[] nums) {
int[] merge = new int[nums.length];
split(nums, merge, 0, nums.length - 1);
}
private void split(int[] nums, int[] merge, int left, int right) {
/**
* 当元素数量少时,使用插入排序
* 之前是切分至剩余一个元素时再合并
*/
if (right - left < 32) {
insertSort(nums, left, right);
return;
}
//寻找中间点,以中间点进行切分
int mid = (left + right) >>> 1;
//切分
split(nums, merge, left, mid);
split(nums, merge, mid + 1, right);
merge(nums, merge, left, mid, mid + 1, right);
System.arraycopy(merge, left, nums, left, right - left + 1);
}
public void insertSort(int[] nums, int left, int right) {
for (int low = left + 1; low <= right; low++) {
int t = nums[low];
int i = low - 1;
while (i >= left && t < nums[i]) {
nums[i + 1] = nums[i];
i--;
}
if (i != low - 1) {
nums[i + 1] = t;
}
}
}
/**
* 合并两个有序数组
*
* @param array 原始数组
* @param merge 合并后的数组
* @param i 第一个有序范围的起始位置
* @param iEnd 第一个有序范围的结束位置
* @param j 第二个有序范围的起始位置
* @param jEnd 第二个有序范围的结束位置
*/
private void merge(int[] array, int[] merge, int i, int iEnd, int j, int jEnd) {
int k = i;
while (i <= iEnd && j <= jEnd) {
if (array[i] < array[j]) {
merge[k] = array[i];
i++;
} else {
merge[k] = array[j];
j++;
}
k++;
}
if (i > iEnd) {
System.arraycopy(array, j, merge, k, jEnd - j + 1);
}
if (j > jEnd) {
System.arraycopy(array, i, merge, k, iEnd - i + 1);
}
}
}
8.快速排序
单边快排(lomuto分区)
- 选择最右侧元素作为基准点
- j 找比基准点小的,i 找比基准点大的,一旦找到,二者进行交换
- 交换时机:j 找到小的,且与 i 不相等
- i 找到 >= 基准点元素后,不应自增
- 最后基准点与 i 交换,i 即为基准点最终索引
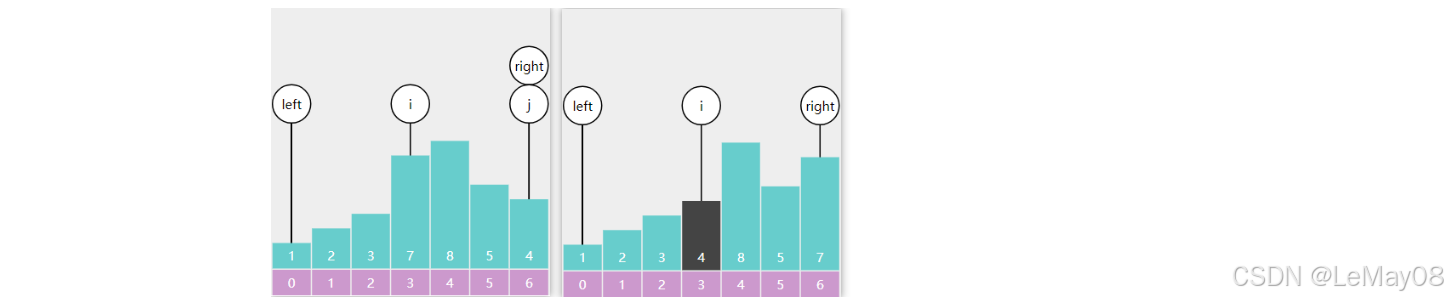
例如:
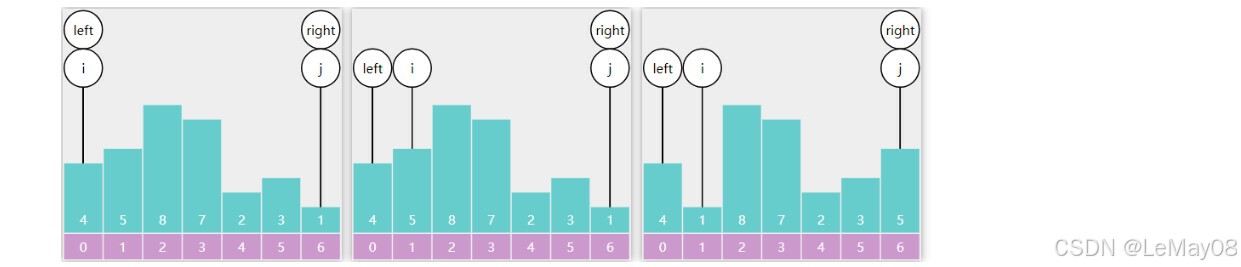
i 和 j 都从左边出发向右查找,i 找到比基准点4大的5,j找到比基准点小的2,停下来交换
i 找到了比基准点大的5,j 找到比基准点小的3,停下来交换
j 到达right 处结束,right 与 i 交换,一轮分区结束
public class QuickSort {
public static void main(String[] args) {
int[] nums = new int[]{3, 2, 1, 4, 5, 7, 9, 6, 8, 0};
new QuickSort().quickSort(nums);
System.out.println(Arrays.toString(nums));
}
/**
* 洛穆托分区方案
*
* @param nums
*/
public void quickSort(int[] nums) {
quick(nums, 0, nums.length - 1);
}
public void quick(int[] nums, int left, int right) {
if (left >= right) {
return;
}
int index = partition(nums, left, right);//返回基准点元素的索引
quick(nums, left, index - 1);
quick(nums, index + 1, right);
}
//分区操作,返回基准点元素的索引
public int partition(int[] nums, int left, int right) {
int value = nums[right];//基准点元素
int i = left;
int j = left;
while (j < right) {
if (nums[j] < value) {//找到比基准点小的值了
if (i != j) {
swap(nums, i, j);
}
i++;
}
j++;
}
swap(nums, i, right);
return i;
}
public void swap(int[] nums, int i, int j) {
int temp = nums[i];
nums[i] = nums[j];
nums[j] = temp;
}
}
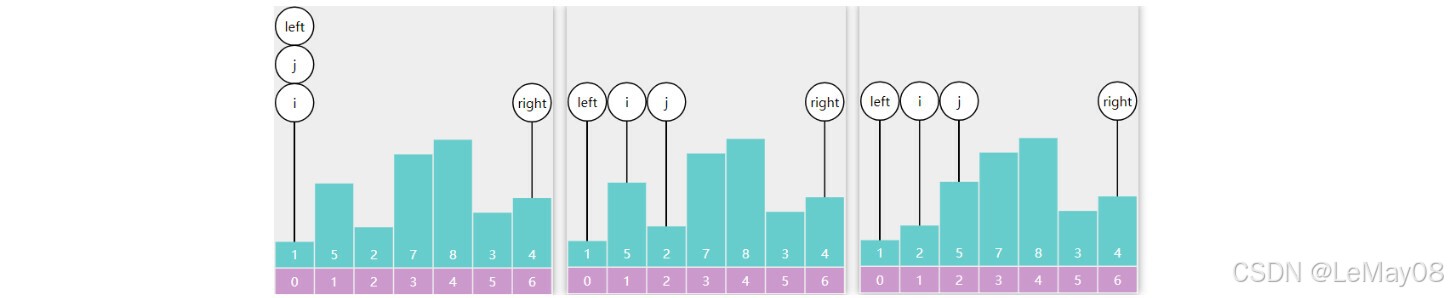
双边快排
- 选择最左侧元素作为基准点
- j 找比基准点小的,i 找比基准点大的,一旦找到,二者进行交换
- i 从左向右
- j 从右向左
- 最后基准点与 i 交换,i 即为基准点最终索引
例:
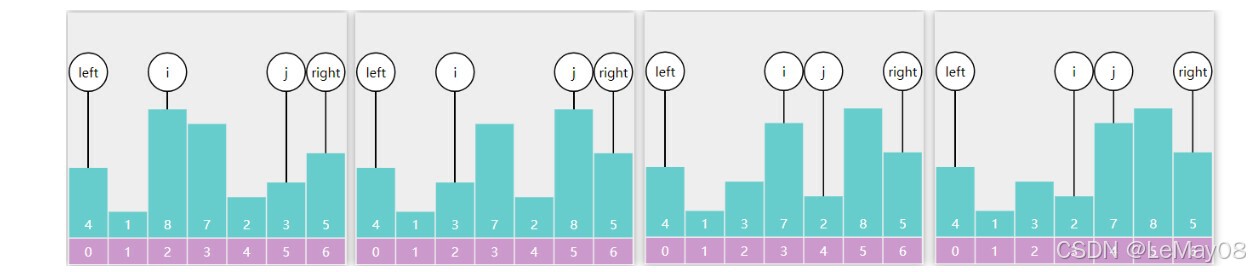
i 找到比基准点大的5停下来,j 找到比基准点小的1停下来(包含等于),二者交换
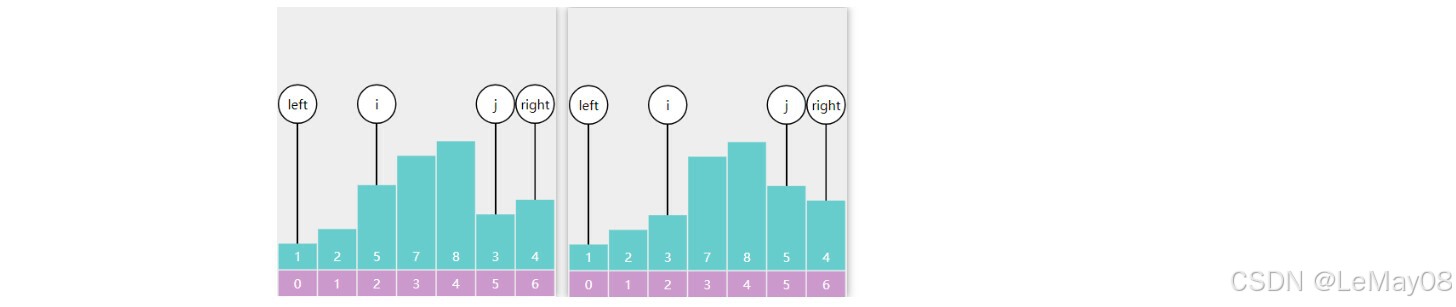
i 找到8,j 找到3,二者交换,i 找到7,j 找到2,二者交换
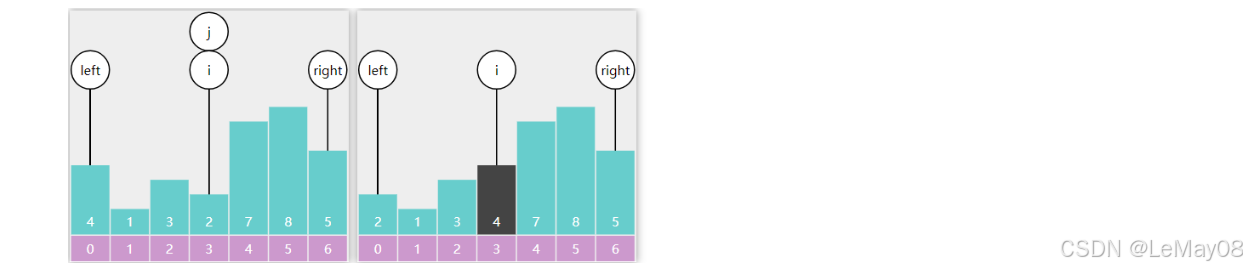
i == j,退出循环,基准点与 i 交换
public int partition(int[] nums, int left, int right) {
int value = nums[left];//基准点元素
int i = left;
int j = right;
while (i < j) {
//j 从右向左找小的
while (i < j && nums[j] > value) {
j--;
}
//i 从左向右找大的
while (i < j && nums[i] <= value) {
i++;
}
//交换
swap(nums, j, i);
}
swap(nums, left, i);
return i;
}
优化
public int partition(int[] nums, int left, int right) {
int index = ThreadLocalRandom.current().nextInt(right - left + 1) + left;
swap(nums, index, left);
int value = nums[left];//随机元素作为基准点元素
int i = left;
int j = right;
while (i < j) {
//j 从右向左找小的
while (i < j && nums[j] > value) {
j--;
}
//i 从左向右找大的
while (i < j && nums[i] <= value) {
i++;
}
//交换
swap(nums, j, i);
}
swap(nums, left, i);
return i;
}
解决数组中重复元素
public int partition(int[] nums, int left, int right) {
int value = nums[left];//随机元素作为基准点元素
int i = left + 1;
int j = right;
while (i <= j) {
//j 从右向左找小的
while (i <= j && nums[i] < value) {
i++;
}
//i 从左向右找大的
while (i <= j && nums[j] > value) {
j--;
}
if (i <= j) {
swap(nums, j, i);
i++;
j--;
}
}
swap(nums, left, j);
return j;
}
9.计数排序
- 确定范围:确定待排序数据中的最大值和最小值。
- 计数:创建一个计数数组,统计每个元素出现的次数。
- 累加计数:将计数数组转化为累加数组,确定每个元素在排序后的位置。
- 排序:将元素按照累加数组中的位置放入输出数组。
public void countSort(int[] nums) {
//1.找出数组中的最大值与最小值
int max = nums[0];
int min = nums[0];
for (int num : nums) {
if (num > max) {
max = num;
}
if (num < min) {
min = num;
}
}
//2.创建新数组,长度是 max - min + 1,用来保存原数组中的数据出现的次数
int[] count = new int[max - min + 1];
for (int num : nums) {
count[num - min]++;
}
//3.循环新数组
int k = 0;
for (int i = 0; i < count.length; i++) {
while (count[i] > 0) {
nums[k++] = i + min;
count[i]--;
}
}
}
10.桶排序
public void bucketSort(int[] nums) {
//1.创建10个桶,每个桶里保存了一定的序列
ArrayList<Integer>[] bucket = new ArrayList[10];
//2.初始化
for (int i = 0; i < bucket.length; i++) {
bucket[i] = new ArrayList<>();
}
//3.把数据放入桶中
for (int num : nums) {
bucket[num / 10].add(num);
}
int k = 0;
//4.排序每个桶内元素
for (ArrayList<Integer> buck : bucket) {
//转数组
int[] array = buck.stream().mapToInt(i -> i).toArray();
insertSort(array);//插入排序
//遍历数组依次放入数组中
for (int v : array) {
nums[k++] = v;
}
}
}
//插入排序
public void insertSort(int[] nums) {
for (int low = 1; low < nums.length; low++) {
int i = low - 1;
int t = nums[low];
while (i >= 0 && t < nums[i]) {
nums[i + 1] = nums[i];
i--;
}
if (i != low - 1) {
nums[i + 1] = t;
}
}
}
通用
public void bucketSort(int[] nums, int range) {
//1.找出数组中的最大值与最小值
int max = nums[0];
int min = nums[0];
for (int num : nums) {
if (num > max) {
max = num;
}
if (num < min) {
min = num;
}
}
//1.创建10个桶,每个桶里保存了一定的序列
ArrayList<Integer>[] bucket = new ArrayList[(max - min) / range + 1];
//2.初始化
for (int i = 0; i < bucket.length; i++) {
bucket[i] = new ArrayList<>();
}
//3.把数据放入桶中
for (int num : nums) {
bucket[(num - min) / range].add(num);
}
int k = 0;
//4.排序每个桶内元素
for (ArrayList<Integer> buck : bucket) {
//转数组
int[] array = buck.stream().mapToInt(i -> i).toArray();
insertSort(array);//插入排序
//遍历数组依次放入数组中
for (int v : array) {
nums[k++] = v;
}
}
}
11.基数排序
基数排序(Radix Sort)是一种非比较型的排序算法,其基本原理是将整数按位数分配,然后按每个位数进行排序。基数排序的稳定性与子排序的稳定性有关。基数排序方法有几种,最常见的是LSD(Least Significant Digit,最低位优先)和MSD(Most Significant Digit,最高位优先)。
public class RadixSort {
public static void main(String[] args) {
String[] phoneNumbers = new String[]{
"13812345678",
"13912345678",
"13612345678",
"13712345678",
"13512345678",
"13412345678",
"15012345678",
"15112345678",
"15212345678",
"15712345678"
};
new RadixSort().radixSort(phoneNumbers, 3);
System.out.println(Arrays.toString(phoneNumbers));
}
public void radixSort(String[] nums, int length) {
//1.准备10个桶并初始化
ArrayList<String>[] buckets = new ArrayList[10];
for (int i = 0; i < buckets.length; i++) {
buckets[i] = new ArrayList<>();
}
//2.依次把数据放入桶内
for (int i = length - 1; i >= 0; i--) {
for (String num : nums) {
buckets[num.charAt(i) - 48].add(num);
}
int k = 0;
for (ArrayList<String> bucket : buckets) {
for (String s : bucket) {
nums[k++] = s;
}
bucket.clear();
}
}
}
}
12.Java排序
Arrays.sort
JDK 7~13 中的排序实现
| 排序目标 | 条件 | 采用算法 |
|---|---|---|
| int[] long[] float[] double[] | size < 47 | 混合插入排序 (pair) |
| size < 286 | 双基准点快排 | |
| 有序度低 | 双基准点快排 | |
| 有序度高 | 归并排序 | |
| byte[] | size <= 29 | 插入排序 |
| size > 29 | 计数排序 | |
| char[] short[] | size < 47 | 插入排序 |
| size < 286 | 双基准点快排 | |
| 有序度低 | 双基准点快排 | |
| 有序度高 | 归并排序 | |
| size > 3200 | 计数排序 | |
| Object[] | -Djava.util.Arrays.useLegacyMergeSort=true | 传统归并排序 |
| TimSort |
JDK 14~20 中的排序实现
| 排序目标 | 条件 | 采用算法 |
|---|---|---|
| int[] long[] float[] double[] | size < 44 并位于最左侧 | 插入排序 |
| size < 65 并不是最左侧 | 混合插入排序 (pin) | |
| 有序度低 | 双基准点快排 | |
| 递归次数超过 384 | 堆排序 | |
| 对于整个数组或非最左侧 size > 4096,有序度高 | 归并排序 | |
| byte[] | size <= 64 | 插入排序 |
| size > 64 | 计数排序 | |
| char[] short[] | size < 44 | 插入排序 |
| 再大 | 双基准点快排 | |
| 递归次数超过 384 | 计数排序 | |
| size > 1750 | 计数排序 | |
| Object[] | -Djava.util.Arrays.useLegacyMergeSort=true | 传统归并排序 |
| TimSort |
- 其中 TimSort 是用归并+二分插入排序的混合排序算法
- 值得注意的是从 JDK 8 开始支持 Arrays.parallelSort 并行排序
- 根据最新的提交记录来看 JDK 21 可能会引入基数排序等优化