235. 二叉搜索树的最近公共祖先

题目链接：235. 二叉搜索树的最近公共祖先
文档讲解：代码随想录
状态：只会昨天的方法，没有想到利用二叉搜索树的性质。

思路：
如果当前节点的值同时小于 p 和 q 的值，说明 p 和 q 都在当前节点的右子树，因此继续在右子树中查找。
如果当前节点的值同时大于 p 和 q 的值，说明 p 和 q 都在当前节点的左子树，因此继续在左子树中查找。
如果当前节点的值在 p 和 q 之间（包括等于 p 或 q），那么当前节点就是 p 和 q 的最近公共祖先。

题解：

public TreeNode lowestCommonAncestor(TreeNode root, TreeNode p, TreeNode q) {
    // 如果当前节点的值同时小于 p 和 q 的值，说明 p 和 q 都在右子树
    if (root.val < q.val && root.val < p.val) {
        return lowestCommonAncestor(root.right, p, q);
    }
    // 如果当前节点的值同时大于 p 和 q 的值，说明 p 和 q 都在左子树
    if (root.val > q.val && root.val > p.val) {
        return lowestCommonAncestor(root.left, p, q);
    }
    // 否则，当前节点就是 p 和 q 的最近公共祖先
    return root;
}

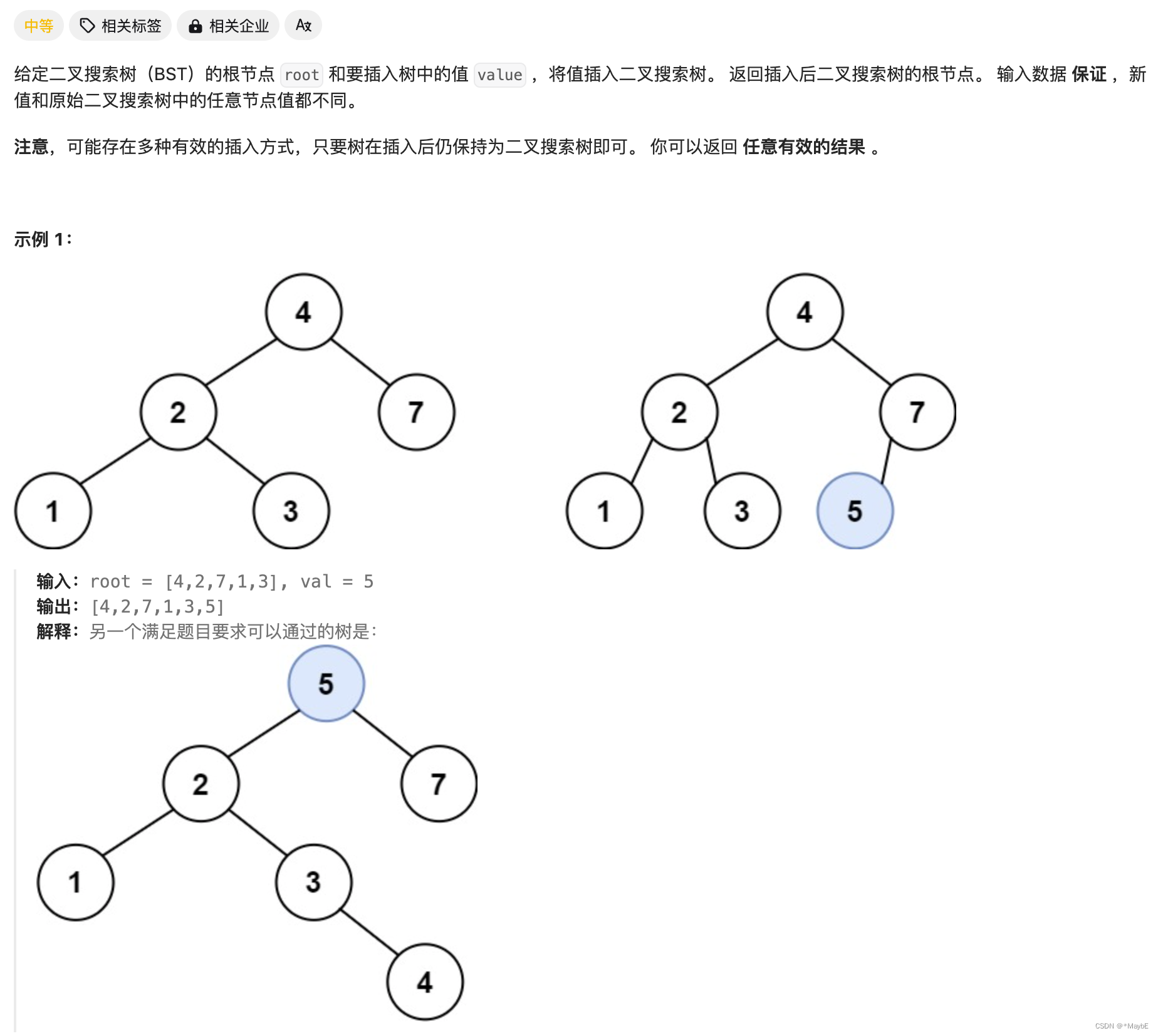
701.二叉搜索树中的插入操作

题目链接：701.二叉搜索树中的插入操作
文档讲解：代码随想录
状态：没做出来

思路：二叉树的插入,递归的返回值肯定是要给root的左右节点的，关键是构建节点的逻辑怎么写

• 在二叉搜索树中，左子树的节点值小于根节点的值，右子树的节点值大于根节点的值。因此，当需要插入一个新节点时，我们从根节点开始比较：
• 如果新节点的值小于当前节点的值，则应该往左子树方向插入；
• 如果新节点的值大于当前节点的值，则应该往右子树方向插入。
• 这样递归地比较，直到找到一个空节点（当前节点的子节点为 null）为止，那么这个空节点就是新节点的插入位置。

题解：

    public TreeNode insertIntoBST(TreeNode root, int val) {
        // 如果根节点为空，创建一个新节点并返回
        // 返回给谁呢?以左下结点x为例,处理后返回了一个新节点y.
        // 后面代码中,root.left = insertIntoBST(root.left, val);表明新节点y被x结点的父节点的left接住了
        // 当在递归过程中找到了正确的插入位置时，会创建一个新节点，并将其返回。在回溯的过程中，将这个新节点连接到其父节点的左子节点或右子节点，确保新节点被正确地接入到树中。
        if (root == null) {
            return new TreeNode(val);
        }

//        不需要去判断左右子树是否为空，因为root==null时会创建新结点
        // 如果要插入的值小于当前节点的值，插入到左子树
        if (val < root.val) {
            // 在左子树中递归插入
            root.left = insertIntoBST(root.left, val);
        }
        // 如果要插入的值大于当前节点的值，插入到右子树
        else if (val > root.val) {
            // 在右子树中递归插入
            root.right = insertIntoBST(root.right, val);
        }

        // 返回根节点，无论是否进行插入
        return root;
    }

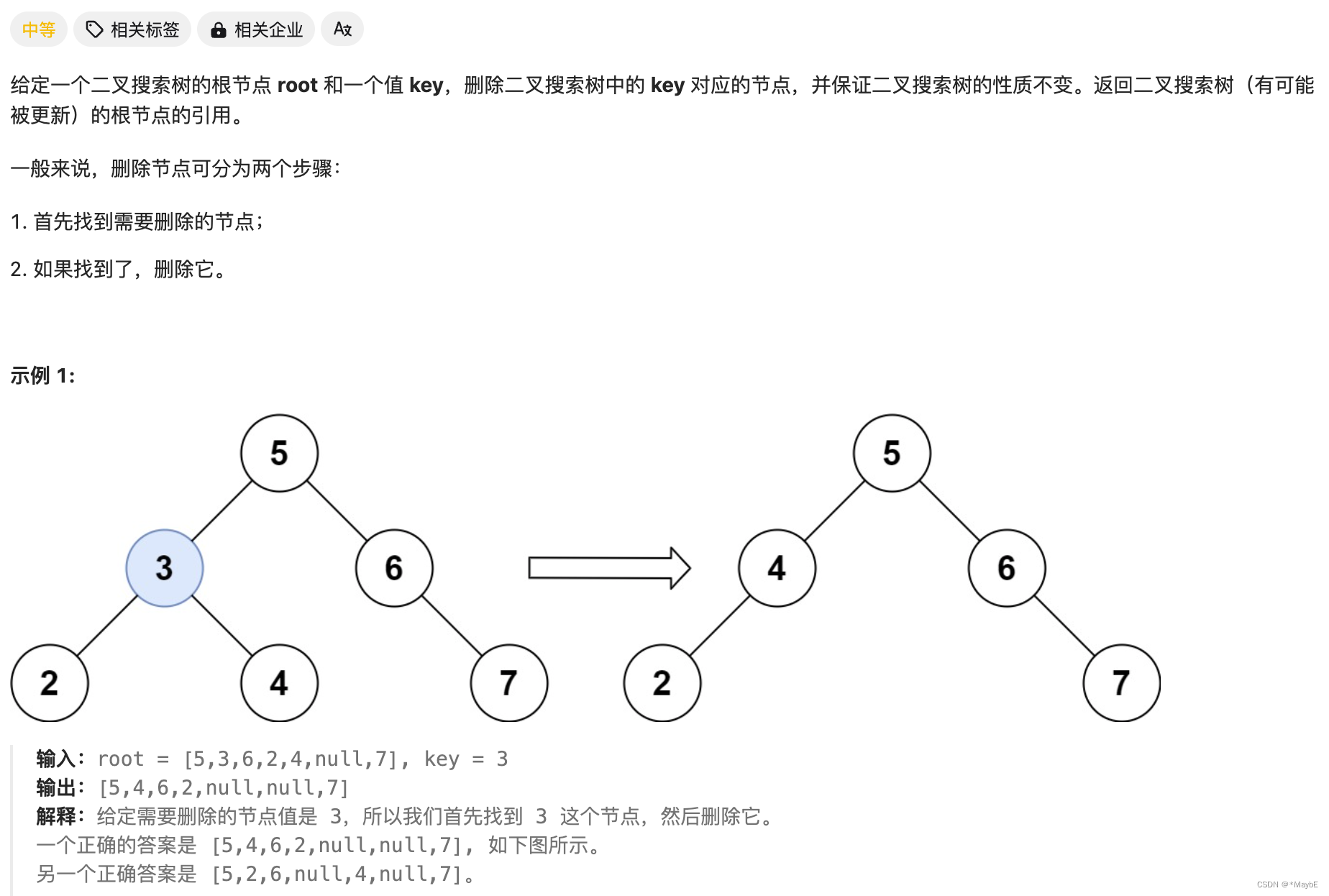
450.删除二叉搜索树中的节点

题目链接：450.删除二叉搜索树中的节点
文档讲解：代码随想录
状态：要考虑的情况太多，没做出来。

思路：
第一种情况：没找到删除的节点，遍历到空节点直接返回了
找到删除的节点
第二种情况：左右孩子都为空（叶子节点），直接删除节点， 返回NULL为根节点
第三种情况：删除节点的左孩子为空，右孩子不为空，删除节点，右孩子补位，返回右孩子为根节点
第四种情况：删除节点的右孩子为空，左孩子不为空，删除节点，左孩子补位，返回左孩子为根节点
第五种情况：左右孩子节点都不为空，则将删除节点的左子树头结点（左孩子）放到删除节点的右子树的最左面节点的左孩子上，返回删除节点右孩子为新的根节点。

题解：

    public TreeNode deleteNode(TreeNode root, int key) {
        if (root == null) {
            return null;
        }
        //如果找到了key
        if (root.val == key) {
            //当key为叶子节点时,返回null
            if (root.left == null && root.right == null) {
                return null;
            } else if (root.left != null && root.right == null) {
                //当右孩子为空
                return root.left;
            } else if (root.right != null && root.left == null) {
                //当左孩子为空
                return root.right;
            } else {
                //左右孩子都不为空时,可以把左孩子转接到右孩子的左叶子结点下
                TreeNode cur = root.right;//cur遍历右孩子
                while (cur.left != null) {
                    cur = cur.left;
                }
                cur.left = root.left;//左孩子转接到右孩子的左叶子结点下
                return root.right;
            }
        } else if (key < root.val) {
            root.left = deleteNode(root.left, key);
        } else {
            root.right = deleteNode(root.right, key);
        }
        return root;
    }