吴恩达机器学习(一)

一、什么是机器学习(what is Machine learning)？

机器学习算法主要有两种机器学习的算法分类

1. 监督学习
2. 无监督学习

两者的区别为是否需要人工参与数据结果的标注

1.监督学习

监督学习：预先给一定数据量的输入和对应的结果即训练集，建模进行拟合，最后让计算机预测未知数据的结果。

监督学习一般有两种：

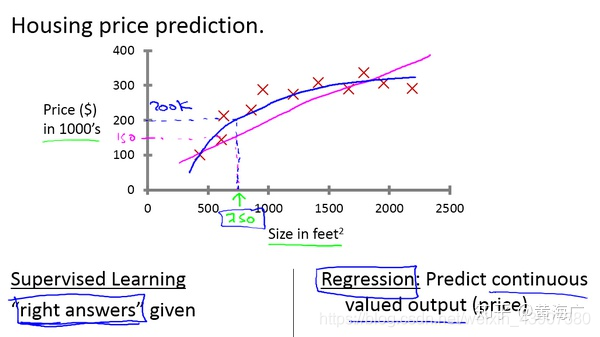
- 回归问题(Regression)

在吴恩达老师课程中，给出了一个房屋价格预测的例子中，给出了一系列的房屋面积数据，以及房屋价格，根据这些数据来搭建一个预测模型，在预测时，给出房屋面积，根据模型得出房屋价格。

- 分类问题(Classification)

分类问题即为预测一系列的离散值。根据一系列数据(同回归问题不一样的是，分类问题的y值是一种离散值，比如0 or 1，又比如cat dog pig)等等，即根据数据预测被预测对象属于哪个分类。在吴恩达老师课程中举了癌症肿瘤这个例子，针对诊断结果，分别分类为良性或恶性。还例如垃圾邮件分类问题，也同样属于监督学习中的分类问题。

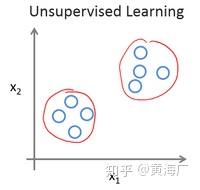
1.无监督学习

相对于监督学习，训练集不会有人为标注的结果（无反馈），无法得知训练集的结果是什么样，而是单纯由计算机通过无监督学习算法自行分析，从而“得出结果”。计算机可能会把特定的数据集归为几个不同的簇，故叫做聚类算法.

在吴恩达老师课程中，举了一个新闻的聚类问题，每天有无数条新闻，一些公司将这些新闻进行分类，将同一个话题的新闻放在一块。

二、单变量线性回归(Linear Regression with One Variable)

1、模型表示

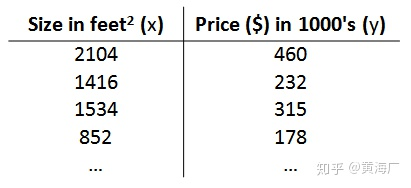
以之前的房屋交易问题为例，回归问题的训练集（Training Set）如下表所示：

描述这个回归问题的标记如下:

• $m$ 代表训练集中实例的数量
• $n$ 代表特征/输入变量
• $x$ 代表目标变量/输出变量
• $y$ 代表目标变量/输出变量
• $h(x)$ 代表假设函数

定义$h(x)={\theta }_0+{\theta }_{1}x$为假设函数，因此之后的任务是求出$\theta$，来拟合给定的数据集。

2、代价函数

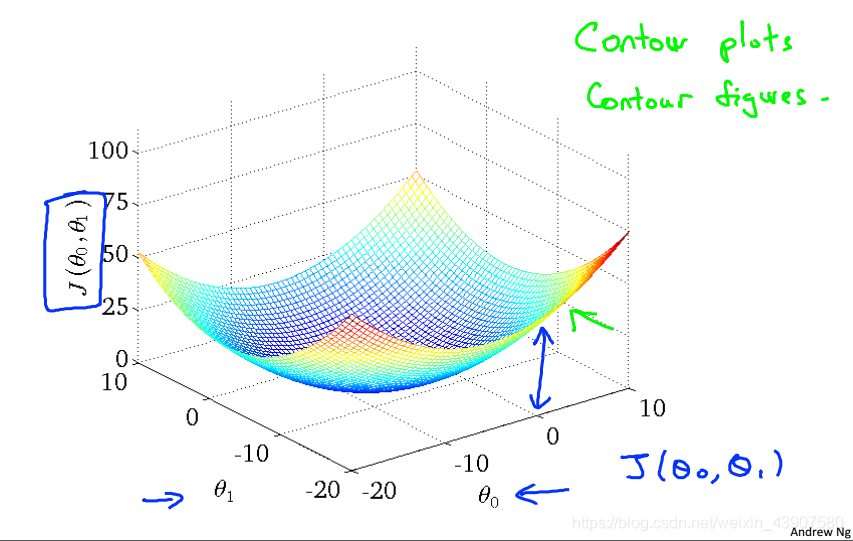
度量建模误差。考虑到要计算最小值，应用二次函数对求和式建模，即应用统计学中的平方损失函数（最小二乘法），定义代价函数为：$$J({\theta }_0,{\theta }_1)=\frac{1}{2m}\sum _{i=1}^n(h_{\theta }(x_i)-y_i{)}^2$$到这之后，只需要求出$J({\theta }_0,{\theta }_1)$的最小值，在这个最小值上的${\theta }_0$${\theta }_1$的值即可。下图是$J({\theta }_0,{\theta }_1)$关于${\theta }_0{\theta }_1$的图像，在图像中即求得在最低点是两个参数的值。

3、梯度下降

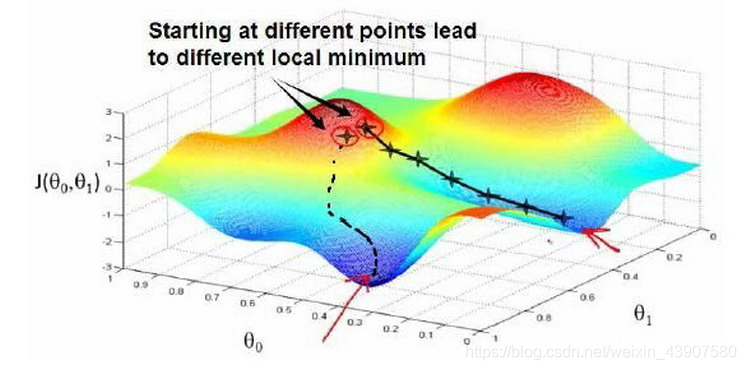
梯度下降的思想是：开始时，我们随机选择一个参数组合即起始点，计算代价函数，然后寻找下一个能使得代价函数下降最多的参数组合。不断迭代，直到找到一个局部最小值(local minimum)，由于下降的情况只考虑当前参数组合周围的情况，所以无法确定当前的局部最小值是否就是全局最小值(global minimum)，不同的初始参数组合，可能会产生不同的局部最小值。

从图上的某一个点，不断朝往下的方向走，直到走到山谷。梯度下降公式：$${\theta }_j={\theta }_j-\alpha \frac{\partial }{\partial {\theta }_j}(J({\theta }_0,{\theta }_1,\cdots ,{\theta }_n))$$
重复上述公式，找到最小值或者局部最小值（即到达山谷）。公式中，学习速率$\alpha$决定了参数值变化的速率即”走多少距离“，而偏导这部分决定了下降的方向即”下一步往哪里“走。

PS:数据集中有多少特征，及定义多少个$\theta$，有可能是$\theta +1$，在更新$\theta$时，所有的$\theta$需要同步更新。

三、多变量线性回归

1、模型表示

比如之前的房屋价格预测例子中，除了房屋的面积大小，可能还有房屋的年限、房屋的层数等等其他特征：

在这次模型中设假设函数为$h_{\theta }(x)={\theta }_0+{\theta }_1{x}_1+{\theta }_2{x}_2+{\theta }_3{x}_3+{\theta }_4{x}_4$

运用线性代数可简化为$$h_{\theta }(x)=\left[\begin{array}{ccccc}{\theta }_0& {\theta }_1& {\theta }_2& {\theta }_3& {\theta }_4\end{array}\right]\left[\begin{array}{c}{x}_0\\ x_1\\ x_2\\ x_3\\ x_4\end{array}\right]={\theta }^{\mathrm{T}}x$$

其中为了实现线性代数的计算，提前假设$x_0$等于1,

2 、多变量梯度下降(Gradient Descent for Multiple Variables)

• 第一步： 还是老规矩写出代价函数
  $$J({\theta }_0,{\theta }_1,\dots ,{\theta }_n)=\frac{1}{2m}\sum _{i=1}^n(h_{\theta }(x^i)-y^i{)}^2$$
• 第二步：写出梯度下降公式：$${\theta }_j={\theta }_j-\alpha \frac{\partial }{\partial {\theta }_j}J({\theta }_0,{\theta }_1,\dots ,{\theta }_n)$$
• 第三步：求出偏导数，带入梯度下降公式：$${\theta }_j={\theta }_j-\alpha \frac{1}{m}\sum _{i=1}^n(h_{\theta }(x^i)-y^i)x_j^i$$

$x_j^i$表示第i个数据样本中的第j个特征

• 第四步：同步更新所有的$\theta$

用线性代数表示为$$\theta =\theta -\alpha \frac{1}{m}(X({\theta }^{\mathrm{T}}X-y))$$

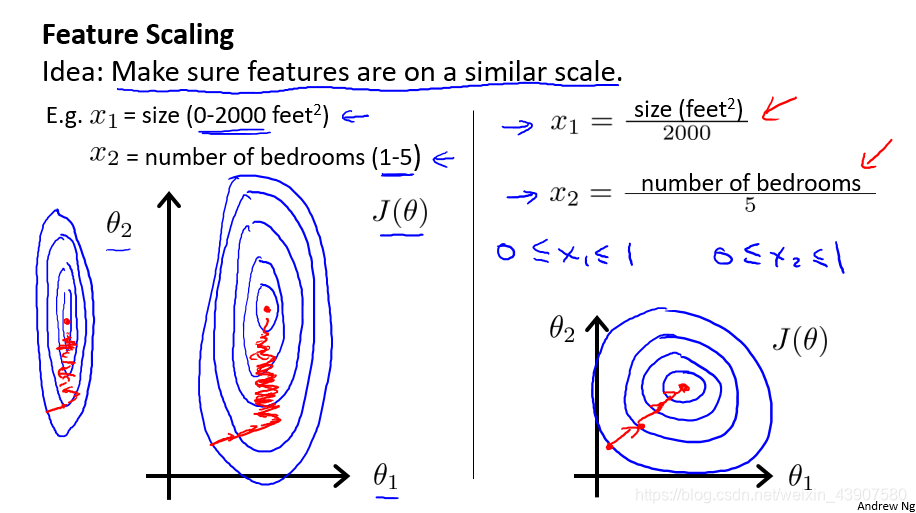
3、特征值缩放

以房价问题为例，假设我们使用两个特征，房屋的尺寸和房间的数量，尺寸的值为 0-2000平方英尺，而房间数量的值则是0-5，以两个参数分别为横纵坐标，绘制代价函数的等高线图能，看出图像会显得很扁，梯度下降算法需要非常多次的迭代才能收敛。

PS:为什么会导致等高线图出现比较扁的情况？
由于$x_1$的尺度比较大(0 ~ 2,000)，而$x_2$的尺度小(0 ~ 5)，因此${\theta }_1$对y的影响大很多。
为什么对特征值进行归一化

为了优化梯度下降的收敛速度，采用特征缩放的技巧，使各特征值的范围尽量一致。均值归一化(Mean normalization)方法更为便捷，可采用它来对所有特征值统一缩放：
$$x_i=\frac{x_i-average(x)}{max(x)-min(x)}$$
使得$x_i$在一个比较小的范围内。这样在进行梯度下降收敛的时候速度会比较快。

这里可能会有疑问，对这些特征进行缩放了，得到的$\theta$值还能一样吗？
注意，这里是对所有的都进行了缩放，不仅是训练集中的数据，还包括我们训练完模型后，对即将需要进行预测的数据也进行了缩放，因此$\theta$值不会发生改变

4、学习速率$\alpha$

$\alpha$的选择不能过大，也不能过小，如果过大代价函数无法收敛，如果过小，代价函数收敛的太慢。当然， 足够小时，代价函数在每轮迭代后一定会减少。可以通过在收敛的过程中绘制图像，来直观的感受$\alpha$的选值，一开始我们可以选择$0.001,0.003,0.01,0.03$等等。

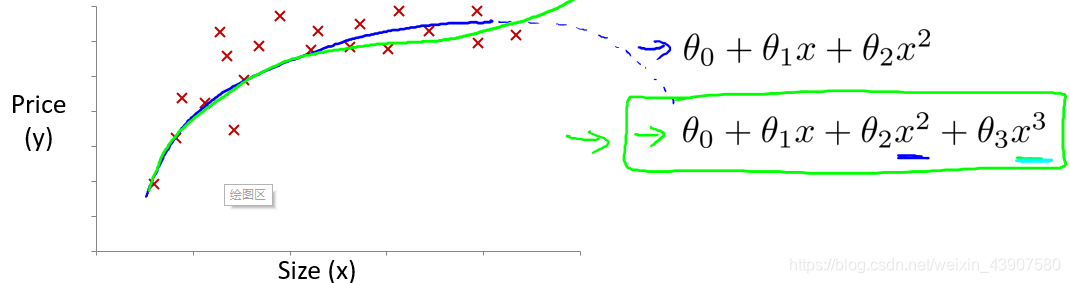
5、多项式回归

线性回归只能以直线来对数据进行拟合，有时候需要使用曲线来对数据进行拟合，即多项式回归(Polynomial Regression)。比如定义一个假设函数$$h_0(x)={\theta }_0+{\theta }_{1}x+{\theta }_2{x}^2+{\theta }_3{x}^3$$

在这里可能有人会有疑问，上述假设函数都涉及到3次方了，怎么还是线性回归，在这里线性回归中的线性的含义：因变量y对于未知的回归参数$\theta$是线性的，注意区分线性回归方程和线性函数，如果方程中包含自变量的N次项，则可以将自变量作为一个整体来考虑

在使用多项式回归时，非常有必要进行特征缩放，比如$x_1$的范围为 $1-1000$，那么 $x_1^2$的范围则为 $1-1000000$，

6、正规方程

正规方程是通过求解下面的方程来找出使得代价函数最小的参数的： $$\frac{\partial }{\partial {\theta }_j}J({\theta }_j)=0$$
假设我们的训练集特征矩阵为$X$并且我们的训练集结果为向量$y$，则利用正规方程解出向量$\theta =(X^{\mathrm{T}}X{)}^{-}{X}^{\mathrm{T}}y$。

学过高数的应该清楚，正规方程的思想和高数中使用偏导数为0求解最值（极值）一样

正规方程推导过程

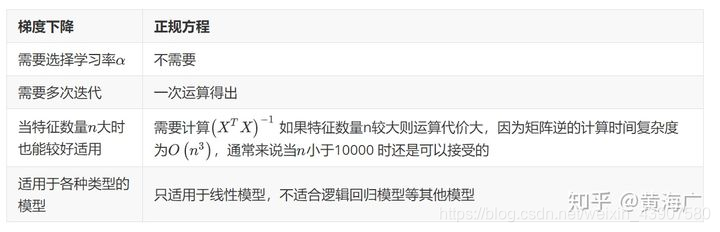
到底梯度下降和正规方程如何选择，可以参考一下表格

四、代码实现

梯度下降

def gradientDescent(X, y, theta, alpha, iters):
    temp = np.matrix(np.zeros(theta.shape))
    parameters = int(theta.ravel().shape[1])
    cost = np.zeros(iters)
    
    for i in range(iters):
        error = (X * theta.T) - y
        
        for j in range(parameters):
            term = np.multiply(error, X[:,j])
            temp[0,j] = theta[0,j] - ((alpha / len(X)) * np.sum(term))
            
        theta = temp
        cost[i] = computeCost(X, y, theta)
        
    return theta, cost

代价函数

def computeCost(X, y, theta):
    inner = np.power(((X * theta.T) - y), 2)
    return np.sum(inner) / (2 * len(X))