计算机中数的表示：在计算机中，能够被硬件直接识别和处理
计算机的运算方法
运算器的设计
6.1无符号数和有符号数
6.1.1无符号数
寄存器的位数，反应了无符号数的表示范围：8位的寄存器，表示范围为0——255,16位的寄存器，表示的范围为0——65535
6.1.2有符号数（包含数值部分和符号部分）
机器数和真值
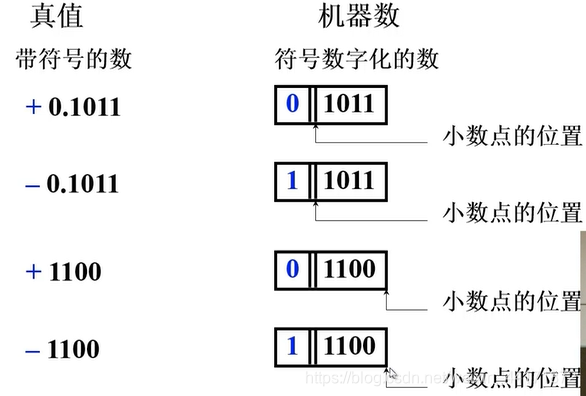
保存在计算机中的数为机器数，真值是平常用的带符号的数值
小数点的位置是以约定的方式给出，没有专门的硬件来表示小数点的位置，设计机器是，默认的将小数点放到符号位的后面。
符号位同样以约定的方式给出，这里默认为符号位在最高位，既最左面的位。
当需要表示的数为整数时，表示的数的小数点的位置位于最右边，既数值的后边，以约定的方式给出。
以上两种都为定点数的表示。

原码表示法：
定义：
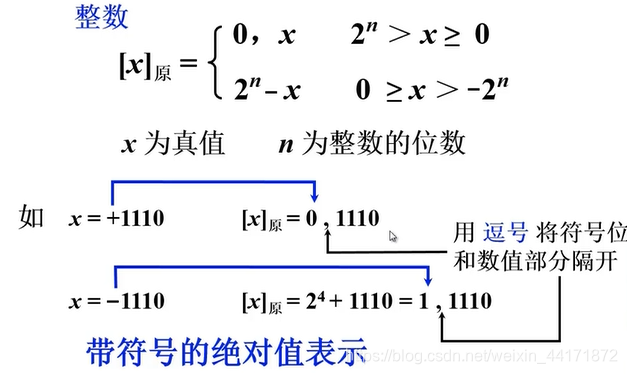
整数：最高位为符号位，正数为0，负数为1，这种方法使 0 有两种表示方法，一种最高位为0，其余为0，另一种最高位为1，其余为0.相当于带符号的绝对值表示。

小数：从真值到原码，如果是整数，加一个符号位，正数加 0，负数加 1，后面的数值部分照抄，就得到原码的机器表示。如果是小数，则小数点前面的一位就用于符号的表示，正数用 0，负数用 1，后面的数值部分照抄，就得到到了机器表示。要表示一个数，需要给出位数，以及位数是否包含符号位。

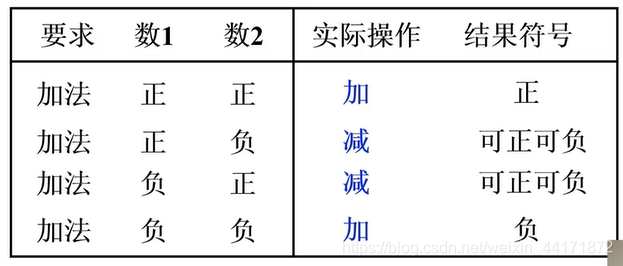
原码的特点：简单、直观，但是使用原码做加法时，会出现如下问题：使用原码进行加法过程，可能做加法，也可能做减法。能不能对加法做归一化处理，使其只做加法运算，既找到一个与负数等价的正数，来代替这个负数，使减法转化成加法

补码表示法
补的概念：在以某个数为模（比如12）的记录数据的过程，将一个数变化成另一个数，既可以向前，也可以向后（比如从 6 变换到 3，则可以减去 3，也可以加上 9，称+9 是 -3 的以 12 为模的补数）。既一个负数加上“模”既得到该负数的补数，一个正数和一个负数互为补数时，他们的绝对值之和为模数。比如存放一个正数，并且规定存放正数的寄存器的位数为 4位，则计数器（模16），每当这个数超过计数器的模，则丢掉模（16）。
补码的定义：
整数：n 为整数的位数，不包括符号位

小数：机器数有位数约定，受到计算机硬件资源的限制。这里小数使用了模 2，故小数点前面有1位，如果模4，小数点前面有两位，模 8的话，小数点前面有 3位……

求补码的快捷方式： 若为正数，则加符号位 0，其余不变。若为符号，则加符号位 1，再将数值位取反，再加上1，既的负数的补码。

同样，由补码转换成原码时，当真值为负时，原码可用补码除符号位不变，每位取反，末位加 1求得。补码的最大的好处在于将减法转换成加法，对运算进行统一。补码形式下，0 具有唯一的表示方法，负值的部分，可以把绝对值最大的负数使用原码中的 负0 的表示方法，故相对于原码，可以多一个负的数值的表示。

反码表示法：相当于在补码表示法中的最后一步，加 1 的步骤，不再需要；同样受到计算机字长的限制，受到计算机资源的限制。
定义：
整数：

小数：

三种机器数小结：最高位为符号位，书写上用“，”（整数）或“.”（小数）将数字部分和符号位隔开；对于正数，原码=补码=反码；对于负数，符号位为1，其数值部分，原码除符号位外每一位取反末位加 1——>补码，原码除符号位外每位取反——>反码；
若机器数字长为 8 位&#x