#写在最前
这里是你的学渣:)
忽然发现数据结构忘得差不多了,从头开始来一遍,就当是复习QAQ
一、数组的定义
若集合S由n个元素,且各元素之间具有一个线性次序,则可将他们存放于起始地址A、物理位置连续的一段存储空间,并统称作数组(array)。通常以A作为该数组的标识,数组A[]中的每一个元素都唯一对应于某一个下标编号。在绝大多数高级程序设计语言中,一般都是从0开始编号。数组可以表示为:
A = {a1,a2, ...,an} ,或者: A[1, n] = {A[1], A[2], ..., A[n]}
数组是一种线性表数据结构(数据排成像一条线一样的结构。每个线性表上的数据最多只有前和后两个方向。)。它用一组连续的内存空间,来存储一组具有相同类型的数据。
这样的结构既有好处也有坏处,好处就是能实现“随机访问”,数组可以快速访问数组中的任意一个数据;坏处就是在进行增删等操作时非常低效,需要移动大量的数据来保证数据的连续性。
二、数组的访问
前面介绍了,数组是用一组连续的内存空间来存储数据的,那么数组是如何实现根据下标随机访问数组元素的呢?
在逻辑上相邻的元素在物理存储上也是相邻的。数组元素可以直接访问:从数组的起始位置A出发,通过一次乘法运算和一次加法运算,便可以得到元素的物理地址。假设数组每个元素占用s个单位空间(如int类型的大小为4个字节),则元素A[i]对应的物理地址为:
A + (i - 1)* s
数组元素的访问操作可以在常时间内完成,所以数组比其他线性结构拥有更高的元素访问效率。
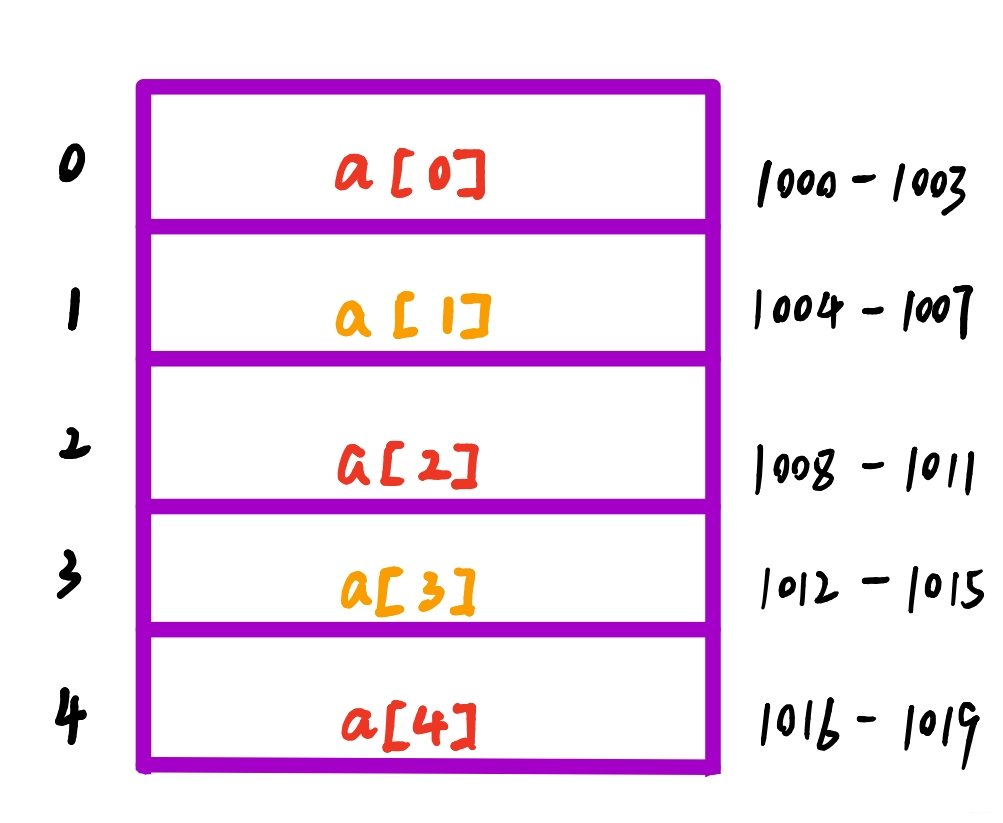
来举个例子吧,创建一个一个长度为5的int类型的数组 int[]a=new int[5]
在这个图中,计算机给数组a[5]分配了一块连续内存空间1000~1019,其中内存块的首地址为A = 1000
计算机会给每个内存单元分配一个地址,计算机通过地址来访问内存中的数据。当计算机需要随机访问数组中的某个元素时,它会首先通过说到的寻址公式 A + (i - 1)* s,计算出该元素存储的内存地址。
三、数组接口
Object:
A // 内部变量,存数组元素的数组
size // 内部变量,记录当前数组元素的个数
数组提供的接口如下:
-
SIZE()
返回数组元素个数。 -
EMPTY()
测试数组是否为空 -
ORDERED()
测试数组元素是否按照升序排列。
伪代码:
ORDERED()
for i <-1 upto size
if A[i - 1] > A[i]
return FALSE
return TRUE
-
GET(pos)
获取数组中特定位置的值,pose是元素下标。 -
SET(pos,e)
设置数组特定位置的值,pose是元素下标,e是新的元素值。 -
FIND(e)
查找数组中是否包含特定元素,若包含则返回元素下标,否则返回NotFound。e为待查找的元素值。
伪代码:
FIND(e)
for i <- 0 upto size
if A[i] == e
return i
return Notfound
- BINARY-SEARCH(e)
使用二叉搜索查找数组中是否包含特定元素,若包含则返回元素下标,否则返回Notfound,e为待查找的元素值。
伪代码:
BINARY-SEARCH(e)
if ORDERED() == FALSE
error "array unsorted"
low <- 0
high <- size - 1
while low <= high
mid <- (low + high) / 2
if A[mid] > e
high <- mid -1
elseif A[mid] < e
low <- mid + 1
else
return mid
return Notfound
- REMOVE(pos)
删除数组特定位置的元素,pos为待删除的元素下标。 - INSERT(pos,e)
在数组的特定位置插入元素,pos为待插入的元素下标,e为待插入元素的值 - SORT()
对数组的元素进行排序,使用冒泡排序。
伪代码:
SORT()
for i <- 0 upto size-1
ordered <- TRUE
for j <- 0 upto size-1-i
if A[j] > A[j+1]
exchange A[j] with A[j+1]
ordered <- FALSE
if ordered == TRUE
break
11. SHUFFLE()
洗牌操作,打乱数组中元素的顺序。
伪代码:
SHUFFLE()
for i <- size downto 1
pos <- rand() % i
exchange A[i-1] with A[pos]
四、在C++上实现
接下来就是大家最关心的问题之如何在C++上实现,这里我们用面向对象的方法,来创建一个数组类。直接上菜:
//Array.h
#ifndef ARRAY_H
#define ARRAY_H
#include <stdlib.h> // standard library标准库头文件
#define DEFAULT_CAPACITY 10 // 宏定义数组的容量
class Array
{
private: //internal data
int* elements; //数组指针
int capacity; //数组容量
int size; //数组实际大小
private: //internal function
void expand(); //增加容量
void shrink(); //缩小容量
void exchange(int a, int b); //交换下标为a、b两个元素之间的位置
public:
/*三种不同的构造函数*/
Array(int c = DEFAULT_CAPACITY);
Array(int const* A, int size);
Array(const Array& v);
~Array(); //析构函数
int& operator[] (int i)const; //运算符[]重载
int getsize()const; //返回size值
bool is_empty()const; //判断是否为空
bool is_ordered()const; //判断是否是升序
int find(int e)const; //返回指定值的元素值
int binary_search(int e)const; //二分搜索
int remove(int low, int high); //移除特定位置的元素
int insert(int pos, int e); //在特定位置插入元素
void push_back(int e); //将元素放到数组最后面
int pop_back(); //弹出最后一个元素
void sort(); //冒泡排序
void shuffle(); //洗牌操作,打乱顺序
};
#endif
这样我们就完成了类内声明啦,接下来在类外定义成员函数:
//Array.cpp
#include "Array.h"
void Array::expand() //增加容量
{
capacity = capacity * 2;
int* old_elements = elements;
elements = new int[capacity];
for (int i = 0; i < size; i++)
{
elements[i] = old_elements[i];
}
delete[] old_elements;
}
void Array::shrink() //缩小容量
{
capacity = capacity / 2;
int* old_elements = elements;
elements = new int[capacity];
for (int i = 0; i < size; i++)
{
elements[i] = old_elements[i];
}
delete[] old_elements;
}
void Array::exchange(int a, int b) //交换下标为a、b两个元素之间的位置
{
int tmp = elements[a];
elements[a] = elements[b];
elements[b] = tmp;
}
int Array::find(int e)const //查找指定元素
{
for (int i = 0; i < size; i++)
{
if (elements[i] = e)
return i;
}
return -1;
}
/*--------------------------------------------------------------------*/
Array::Array(int c) //生成空数组
{
capacity = c;
size = 0;
elements = new int[capacity];
elements[0] = 0;
}
Array::Array(int const* A, int Size) //拷贝参数A中size范围内的的元素
{
size = Size;
capacity = size + 1;
elements = new int[capacity];
for (int i = 0; i < size; i++)
{
elements[i] = A[i];
}
}
Array::Array(const Array& v) //拷贝数组v
{
size = v.getsize();
capacity = v.getsize() + 1;
elements = new int[capacity];
for (int i = 0; i < v.getsize(); i++)
{
elements[i] = v[i];
}
}
Array::~Array() //析构函数
{
delete[] elements;
}
int& Array::operator[] (int i)const
{
return elements[i];
}
int Array::getsize()const //返回size值
{
return size;
}
bool Array::is_empty()const //判断是否为空
{
return size == 0;
}
bool Array::is_ordered()const //判断是否是升序
{
for (int i = 1; i < size; i++)
{
if (elements[i - 1] > elements[i])
return false;
}
return true;
}
int Array::binary_search(int e)const //二分搜索
{
if (is_ordered() == false)
{
return -1;
}
int low = 0;
int high = size - 1;
while (low <= high)
{
int mid = (low + high) / 2;
if (mid < e)
{
low = mid + 1;
}
else if (mid > e)
{
high = mid - 1;
}
else
{
return mid;
}
}
return -1;
}
int Array::remove(int low, int high) //移除特定位置的元素
{
if (high > size - 1)
high = size - 1;
int delta = high + 1 - low; //delta代表要移除元素的个数
for (int i = high + 1; i < size; i++)
{
elements[i - delta] = elements[i]; //如果无法理解就想象要删除两个相邻的元素的话需要怎么操作
}
size = size - delta;
if (size < capacity / 2)
shrink();
return delta;
}
int Array::insert(int pos, int e) //在特定位置插入元素
{
if (pos > size)
pos = size;
if (size + 1 > capacity)
expand();
for (int i = size - 1; i >= pos; i--)
{
elements[i + 1] = elements[i];
}
elements[pos] = e;
size++;
return pos;
}
void Array::push_back(int e) //将元素放到数组最后面
{
insert(size, e);
}
int Array::pop_back() //弹出最后一个元素
{
int last = elements[size - 1];
remove(size - 1, size - 1);
return last;
}
void Array::sort() //冒泡排序,如果没看懂就去看看前面的动图
{
for (int i = 0; i < size - 1; i++)
{
bool ordered = true;
for (int j = 0; j < size - 1 - i; j++)
{
if (elements[j] > elements[j + 1])
{
exchange(j, j + 1);
ordered = false;
}
}
if (ordered == true)
break;
}
}
void Array::shuffle() //洗牌操作,打乱顺序
{
for (int i = size; i > 0; i--)
{
exchange(i - 1, rand() % i); //rand() % i会产生一个0 - (i-1)的随机数
}
}
那么接下来就写一个主函数测试一下部分功能:
//main.cpp
#include <iostream>
#include "Array.h"
using namespace std;
int main()
{
int G[5] = { 5,4,3,2,1 };
//三种不同方法来创建实例
Array A(G, 5);
Array B(DEFAULT_CAPACITY);
Array C(A);
for (int i = 0; i < A.getsize(); i++) //打印数组A的全部元素
{
cout << A.operator[](i) << " ";
}
cout << endl;
for (int i = 0; i < C.getsize(); i++) //打印数组C的全部元素
{
cout << C.operator[](i) << " ";
}
cout << endl;
A.sort(); //冒泡排序的函数
for (int i = 0; i < A.getsize(); i++)
{
cout << A.operator[](i) << " ";
}
cout << endl;
return 0;
}
预期的结果应该是:
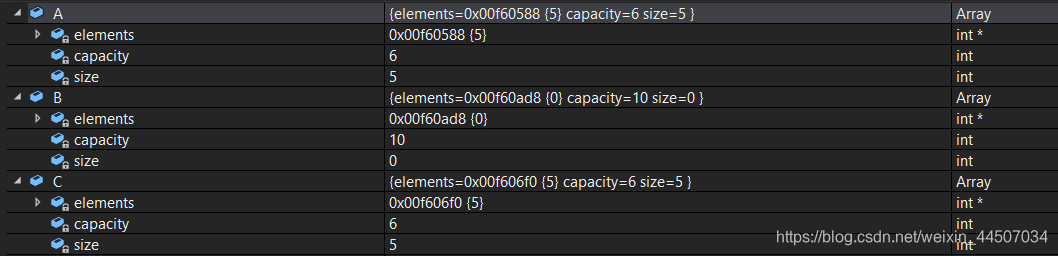
A={5, 4, 3, 2, 1}, size = 5,capacity = 6;
B={}, size = 0,capacity = 10;
C={5, 4, 3, 2, 1}, size = 5,capacity = 6;
排序之后的A应该为{1, 2, 3, 4, 5}
插入断点调试,可以看到:
再看看输出:
与预期结果一致。那么其他函数我就不一一测试了,有兴趣可以自行尝试。
那么就到这里为止啦,每个字都是亲手敲的,希望能够帮上忙~peace!