力扣： 222. 完全二叉树的节点个数 - 力扣（LeetCode）

给你一棵  完全二叉树 的根节点  root ，求出该树的节点个数。

完全二叉树 的定义如下：在完全二叉树中，除了最底层节点可能没填满外，其余每层节点数都达到最大值，并且最下面一层的节点都集中在该层最左边的若干位置。若最底层为第  h 层（从第 0 层开始），则该层包含  1~ 2 h 个节点。 

示例 1：

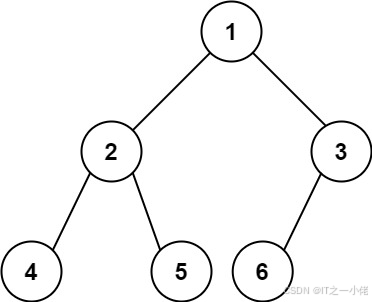
输入：root = [1,2,3,4,5,6] 输出：6

示例 2：

输入：root = [] 输出：0

示例 3：

输入：root = [1] 输出：1 

提示：

• 树中节点的数目范围是[0, 5 * 104]
• 0 <= Node.val <= 5 * 10^4
• 题目数据保证输入的树是 完全二叉树

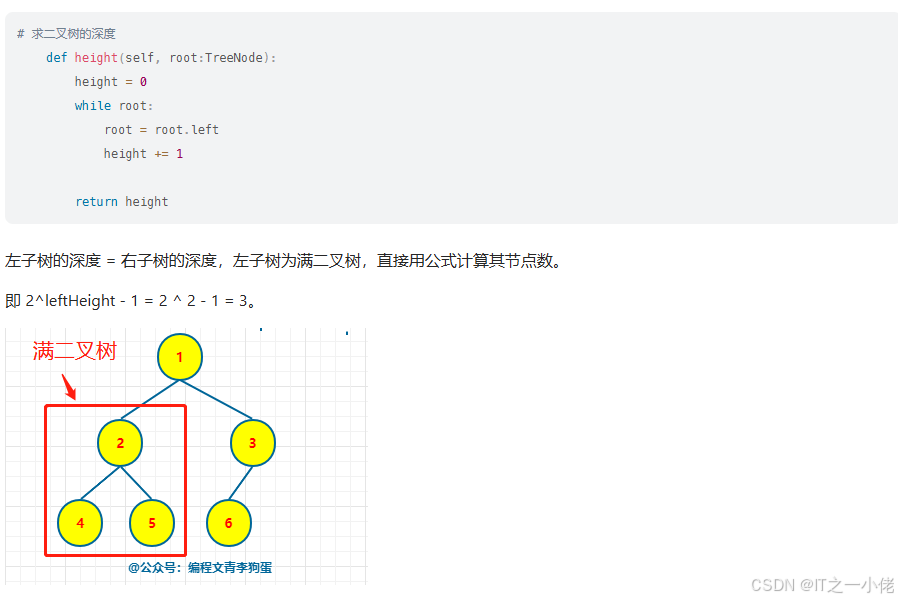
本地运行代码：

# !/usr/bin/env python
# -*- coding: utf-8 -*-
# @File  : 完全二叉树的节点个数.py
# @Author: dgw
# @Date  : 2024-12-31 9:54
# Definition for a binary tree node.
class TreeNode(object):
    def __init__(self, val=0, left=None, right=None):
        self.value = val
        self.left = left
        self.right = right


class Solution(object):

    def crate_tree(self, nums, index):
        if not nums:
            return None
        if index >= len(nums):
            return None
        root = TreeNode(nums[index])
        root.left = self.crate_tree(nums, index * 2 + 1)
        root.right = self.crate_tree(nums, index * 2 + 2)
        return root

    def height(self, root):
        """求二叉树的高度"""
        height = 0
        while root:
            root = root.left
            height += 1
        return height

    def count_nodes(self, root):
        # 空树，节点数为 0
        if root is None:
            return 0
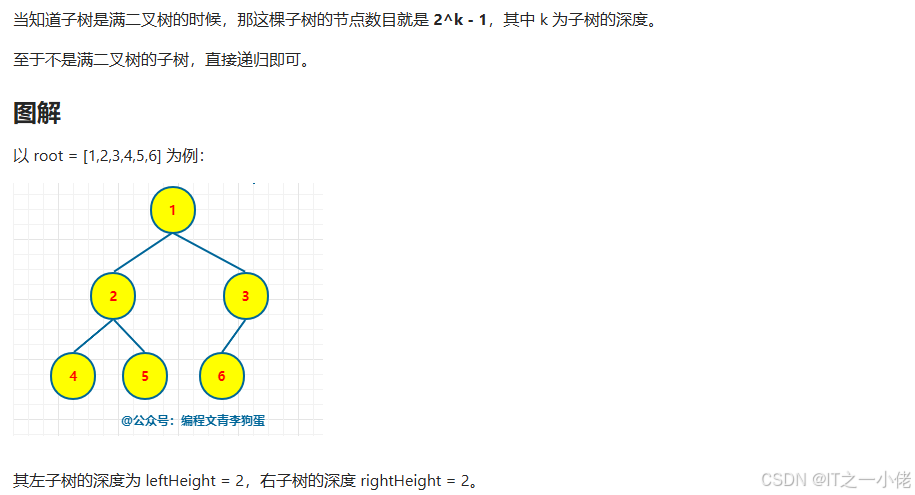
        # 求左子树和右子树的深度
        left_count = self.height(root.left)
        right_count = self.height(root.right)

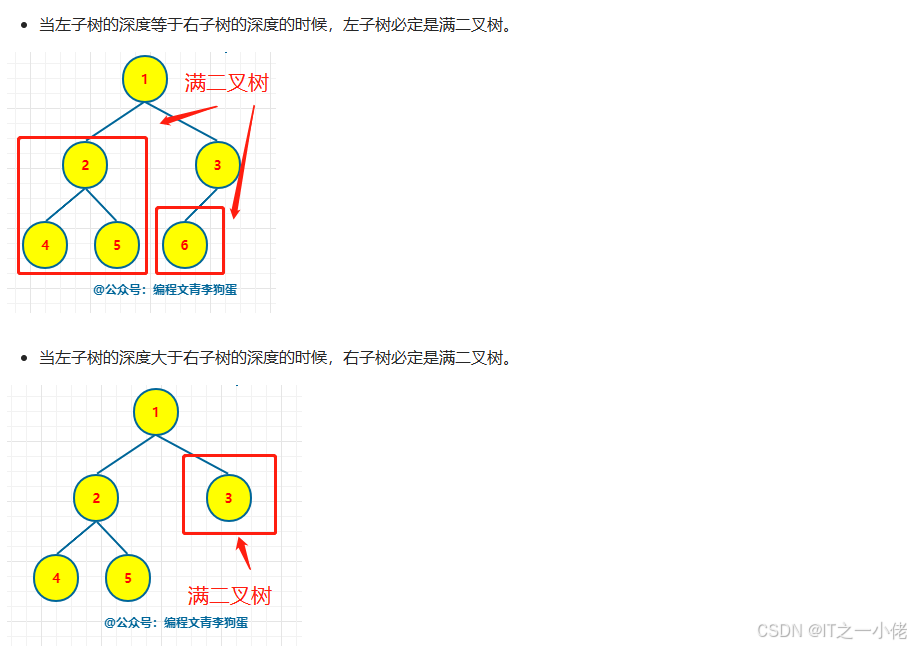
        # 如果左子树的深度 = 右子树的深度，左子树为满二叉树
        # 节点数 = 左子树的深度 + 右子树的深度 + 根节点
        if left_count == right_count:
            return (2 ** left_count - 1) + self.count_nodes(root.right) + 1
        # 如果左子树的深度 ＞ 右子树的深度，右子树为满二叉树
        # 节点数 = 左子树的深度 + 右子树的深度 + 根节点
        else:
            return (2 ** right_count - 1) + self.count_nodes(root.left) + 1


if __name__ == '__main__':
    lst = [0, 1, 2, 3, 4, 5, 6, 7, 8, 9]
    s = Solution()
    ret = s.crate_tree(lst, 0)
    print(ret.value)
    res = s.count_nodes(ret)
    print(res)

运行结果：