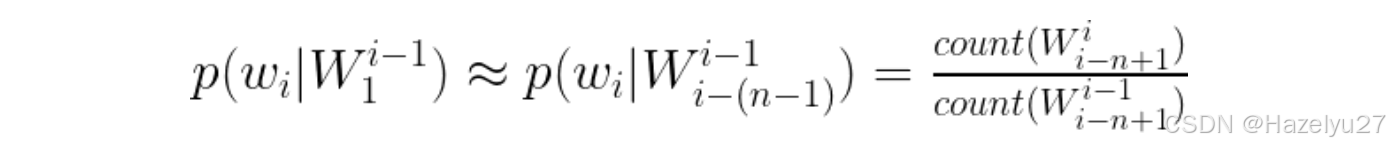1. 用pytorch写一个self-attention
继承pytorch.nn.Module的类
代码:
import torch
import torch.nn as nn
import torch.nn.functional as F
class SelfAttention(nn.Module):
def __init__(self, embed_size): # (B,T,C)
super(SelfAttention, self).__init__()
self.embed_size = embed_size
self.query = nn.Linear(embed_size, embed_size)
self.key = nn.Linear(embed_size, embed_size)
self.value = nn.Linear(embed_size, embed_size)
def forward(self, x):
batch_size, seq_length, embed_size = x.shape
Q = self.query(x)
K = self.key(x)
V = self.value(x)
# transpose可以转置,-2,-1是把-2和-1维度的做转置,batchsize维度是不变的
QK = Q @ K.transpose(-2,-1) # Q: (B,T,C) K:(B,C,T)
QK = QK / torch.sqrt(embed_size) # QK: (B,T,T)
attention_weights = F.softmax(QK, dim=-1) # attentionweights: (B,T,T)
output = attention_weights @ V # V:(B,T,C)
return output # output:(B,T,C)
# 自己写测试用例
embed_size = 64
seq_length = 10
batch_size = 1
x = torch.randn(batch_size, seq_length, embed_size)
self_attention = SelfAttention(embed_size)
output = self_attention(x)
print("output shape", output.shape)注意点:
1. 构造函数是__init__(), 继承类是写在了class后面的括号里。F来自torch.nn.Functional
2. __init__和forward都要写self,在__init__里面定义公式
3. QKV都是输入的x根据线性模型得到的。线性层要定义它的输入输出维度。
4. 转置用transpose,sqrt是用torch库里的
5. softmax记得写dim
6. x输入的维度是:batch_size, seq_length, embed_size 批次大小,序列长度,单词长度。
7. 创建随机数:torch.randn()
根据以上的代码再增加mask:mask multi-head attention
def forward(self, x,mask = None):
batch_size, seq_length, embed_size = x.shape
Q = self.query(x)
K = self.key(x)
V = self.value(x)
# transpose可以转置,-2,-1是把-2和-1维度的做转置,batchsize维度是不变的
QK = Q @ K.transpose(-2,-1) # Q: (B,T,C) K:(B,C,T)
QK = QK / torch.sqrt(torch.tensor(embed_size)) # QK: (B,T,T)
if mask is not None:
QK = QK.masked_fill(mask ==0, float('-inf'))
attention_weights = F.softmax(QK, dim=-1) # attentionweights: (B,T,T)
output = attention_weights @ V # V:(B,T,C)
return output # output:(B,T,C)masked_fill函数:mask中取值为True位置对应于QK的相应位置用value填充。value是float的inf,负无穷。
mask应该是一个类似三角形的矩阵,矩阵上三角区域都为负无穷。
创建mask:
mask = torch.tril(torch.ones(seq_length, seq_length)).unsqueeze(0) == 1torch.tril 函数接受一个二维张量,并返回一个下三角版本的张量。在返回的张量中,原张量的上三角部分(即对角线右上方的元素)被设置为 0,而下三角部分(包括对角线和对角线左下方的元素)保持不变。这意味着每个元素可以“看到”它在序列中的前面的元素和自己,因为这些位置不为零。
2. 有哪些对文本特征进行编码的方式?
(1)one-hot是最简单的一种处理方式。通俗地去讲,把语料中的词汇去重取出,按照一定的顺序(字典序、出现顺序等)排列为词汇表,则每一个单词都可以表示为一个长度为N的向量,N为词汇表长度,即单词总数。该向量中,除了该词所在的分量为1,其余均置为0。
(2)n-gram可以表示单词间的位置关系所反映的语义关联。
其实是利用贝叶斯公式。一个句子出现的概率分解成单词出现概率的条件概率公式:
利用马尔可夫假设,取该词出现的概率仅依赖于该词前面的n-1个词,这就是n-gram模型的思想
(3)共现矩阵
在文本中形成一个窗口,假设每两个词之间的相关性与两者的位置关系有关,那么根据位置关系建立对称的距离矩阵就是共现矩阵。共现矩阵的每一行为这个单词的向量表示。
但这种数据仍然会有维度灾难。可以通过SVD或者PCA一些降维方法进行降维。
(4)NLM Neural language Model
NLM的目的是:相似含义的词在目标向量空间中的距离比不相关词的距离更近。
NLM的输入:(Context(w),w),Context(w)是w的前n-1个词。输出是概率:所有词构成的向量,向量第i个位置的值表示w后面接第i个词的概率。神经网络用softmax进行过归一化。
3. word embedding是什么?
词嵌入算法有:Word2vec, fasttext, Glove等。
word embedding可以将单词从稀疏的高维空间转换到一个连续的低维空间。
Word Embedding:单词嵌入,就是把X所属空间的单词映射为到Y空间的多维向量,那么该多维向量相当于嵌入到Y所属空间中。与one-hot编码和word class相比,词嵌入可以将更多的信息塞入更低的维度中。
应该就是新建一个特征空间,把这个词映射到特征空间中。映射方式是用无监督模型来做。它通过上下文来理解一个词的含义。如果两个词常在同一篇文字中出现,说明两个向量比较接近。
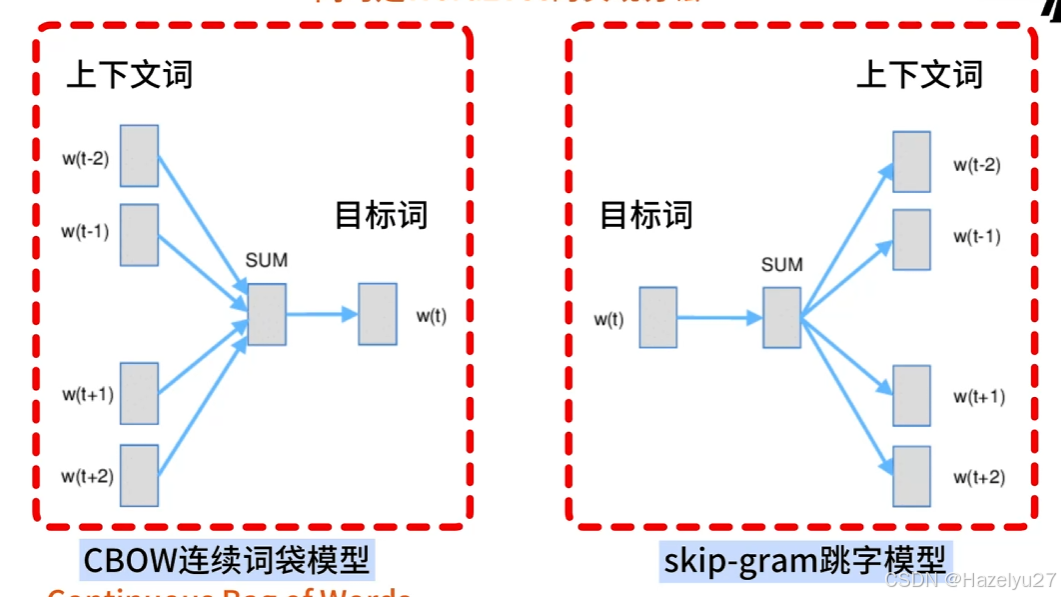
word embedding是基于NLM模型的。它有两种类型:CBOW和Skip-gram
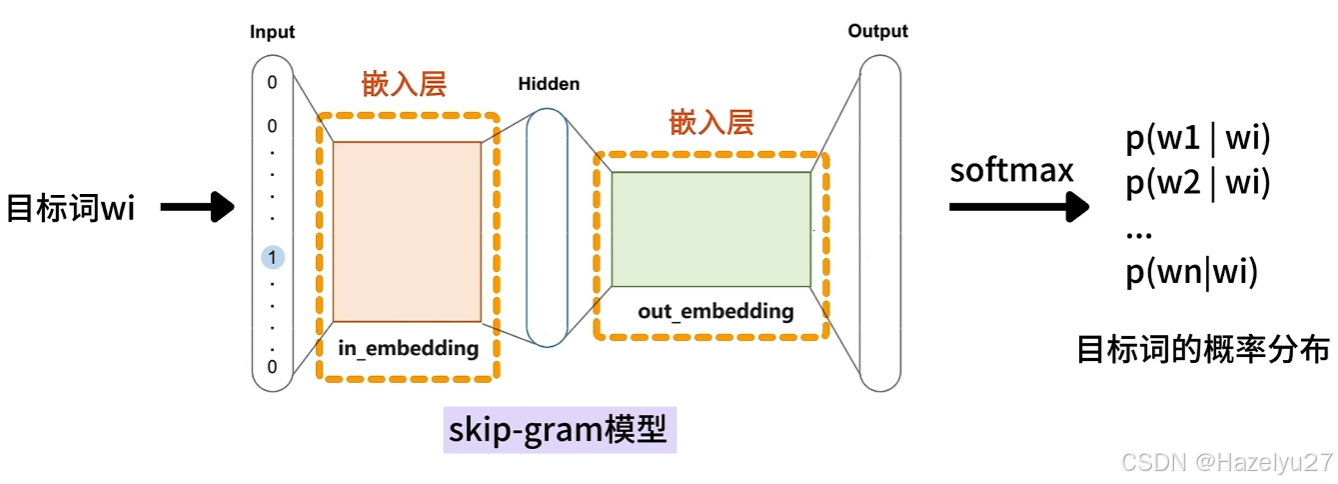
(1)word2vec的算法流程:
首先,对一个句子进行分词,并使用one-hot向量进行编码。假设语料库里5000个词,那么一个句子的矩阵形状为(n,5000). 找到一个嵌入矩阵(5000, 128),两者相乘就能得到(n,128)的嵌入向量。
嵌入矩阵的每一行表示每个单词的词向量。所以重点是求词嵌入向量(embeddings)。
(2)Word2vec连续词袋模型 CBOW
CBOW:根据上下文词汇预测目标词汇;Skip-gram根据目标词汇预测上下文词汇。
CBOW是一个神经网络,接收一个窗口内的上下文词语,并返回目标词。embedding层是CBOW里面的一层,通过训练这个神经网络得到训练好的embedding层,就是词嵌入向量。embedding层就可以当成是一个神经网络,有V个隐藏层,n个输出神经元,embedding大小为(V*N)
(3)Skip-gram:同样是迭代出词向量矩阵embeddings
但是,它的输入是上下文词,输出是目标词,模型迭代的目标是让上下文词与目标词更接近,而非上下文词和目标词更远。
(4)Skipgram和CBOW的优缺点是什么?
skipgram对低频词(罕见词)的效果更好,对单独的上下文更敏感。能学习到更精准的词嵌入。但是,它需要对每个词进行更多的词嵌入,训练速度比CBOW更慢。
CBOW训练速度更快,每次只针对一个词。在处理常见词的效果好,因为它利用上下文的平均来预测当前词。但是它对罕见词的效果更差,对噪声数据很敏感。
4. 根据二叉树的后序和中序,写前序排列。
#include <bits/stdc++.h>
using namespace std;
void tree(string a, string b){
if(a.size()==0 || b.size() ==0) return;
char ch = b[b.size()-1];
cout<<ch;
int idx = a.find(ch);
tree(a.substr(0,idx),b.substr(0,idx));
tree(a.substr(idx+1), b.substr(idx, b.size()-idx-1));
}
int main(){
string midstr, backstr;
cin>>midstr>>backstr;
tree(midstr, backstr);
return 0;
}c++注意:可以直接用str.find(ch)找到string里对应char的索引。另外,substr的参数为:(起始位置,长度)
vector找对应元素下标:
find(nums.begin(),nums.end(),3) - nums.begin();建树的写法:
TreeNode* findroot(string a, string b) {
if (a.size() == 0 || b.size() == 0) {
return nullptr;
}
char ch = b[b.size() - 1];
TreeNode* cur = new TreeNode(ch);
int x = a.find(ch);
cur->left = findroot(a.substr(0, x), b.substr(0, x));
cur->right = findroot(a.substr(x + 1), b.substr(x, b.size() - x - 1));
return cur;
}
int main() {
string midres = "4251637";
string backres = "4526731";
TreeNode* root = findroot(midres, backres);
fronttravel(root);
return 0;
}leetcode hot100中一题:用前序和中序建树
TreeNode* findtree (vector<int> a, vector<int> b){
if(a.size() == 0 || b.size() ==0) return nullptr;
int rootval = a[0];
int rootidx = find(b.begin(),b.end(),rootval) - b.begin();
vector<int> lefttree1=a,righttree1 = a, lefttree2=b,righttree2 = b;
lefttree1.assign(lefttree1.begin()+1, lefttree1.begin()+rootidx+1);
righttree1.assign(righttree1.begin()+rootidx+1, righttree1.end());
lefttree2.assign(lefttree2.begin(), lefttree2.begin()+rootidx);
righttree2.assign(righttree2.begin()+rootidx+1, righttree2.end());
TreeNode * cur = new TreeNode(rootval);
cur->left = findtree(lefttree1, lefttree2);
cur->right = findtree(righttree1, righttree2);
return cur;
}
TreeNode* buildTree(vector<int>& preorder, vector<int>& inorder) {
TreeNode * root = findtree(preorder, inorder);
return root;
}主要是他是vector,会比用string麻烦,但常规应该是用vector比较多。vector主要麻烦在切片,得用str.assing(), 里面放左闭右开区间。
python写法:
注意找一个列表元素为n的下标index:vec.index(n)
class treeNode():
def __init__(self,value):
self.val = value
self.left = None
self.right = None
midvec = [4,2,5,1,6,3,7]
backvec = [4,5,2,6,7,3,1]
def fronttravel(head):
if head is None:
return
print(head.val)
fronttravel(head.left)
fronttravel(head.right)
def maketree(midvec, backvec):
if len(midvec) == 0:
return None
val = backvec[-1]
idx = midvec.index(val)
cur = treeNode(val)
cur.left = maketree(midvec[0:idx], backvec[0:idx])
cur.right = maketree(midvec[idx+1:],backvec[idx:-1])
return cur
if __name__=="__main__":
root = maketree(midvec, backvec)
fronttravel(root)
5. 快速排序python写法,以及时间复杂度
完全不同于c++,直接取出列表中比它小的和列表中比它大的,再拼起来
注意取列表元素的写法:less = [ i for i in arr[i:] if i <= pivot]
def quick_sort(arr):
if len(arr) < 2:
return arr
pivot = arr[0]
less = [ i for i in arr[1:] if i <= pivot]
greater = [i for i in arr[1:] if i > pivot]
return quick_sort(less) + [pivot] + quick_sort(greater)
arr = [10,9,8,7,6,5,4,3,2,1]
print(quick_sort(arr))时间复杂度分析:
最好情况 在最好的情况下,每次分区都恰好将数组分成两个大小大致相等的子数组。这意味着每次递归调用处理的数组长度大约是前一次的一半。在这种情况下,快速排序展现出最佳性能。
- 每一层递归的总工作量大约是 O(n)O(n)O(n)(每个元素都需要与基准值进行比较一次)。
- 递归的深度是 O(logn)O(\log n)O(logn),因为数组大小每次都减半。
平均情况,递归树也是nlogn。
最坏情况 最坏情况发生在每次选择的基准元素恰好是当前数组中的最小值或最大值。这种情况下,每次分区操作只能将数组分为一个元素和其余元素两部分,导致递归树极不平衡。
为了避免最坏情况的发生,常见的做法是通过随机选择基准元素来尝试保证分区的平衡,或者使用三数中值法(Median-of-three)来选择基准元素,即从数组的首元素、中间元素和尾元素中选取中间值作为基准元素,这有助于减少不平衡的发生几率。
6. python 标准库:队列、栈、优先队列
队列:例子:用python实现层序遍历(用到队列)
主要就是push为put(), pop为get() 并且一个get可以同时弹出并返回。也不用指针,都直接用点号。
class TreeNode:
def __init__(self,value):
self.val = value
self.left = None
self.right = None
def layertravel(root):
que = queue.Queue()
que.put(root)
while not que.empty():
cur = que.get()
if cur is not None:
print(cur.val)
que.put(cur.left)
que.put(cur.right)优先队列:例子为10000个数找前10个
注意random.randint()生成随机元素
__lt__是用于复杂比较的
from queue import PriorityQueue
import random
class numbers():
def __init__(self,value):
self.val = value
def __lt__(self, other):
return self.val > other.val
if __name__ == "__main__":
nums = []
for i in range(10000):
nums.append(numbers(random.randint(1,10000)))
pq = PriorityQueue()
for i in range(10000):
pq.put(nums[i])
for i in range(10):
print(pq.get().val)c++写法:这里要建大根堆。
#include <queue>
#include <iostream>
#include <stdlib.h>
using namespace std;
class cmp {
public:
bool operator() (int a, int b) {
return a < b;
}
};
priority_queue<int, vector<int>, cmp> pq;
int main() {
const int N = 10000;
vector<int> nums;
for (int i = 0; i < N; i++) {
nums.push_back(rand());
}
for (int i = 0; i < N; i++) {
pq.push(nums[i]);
}
for (int i = 0; i < 10; i++) {
cout << pq.top() << " ";
pq.pop();
}cout << endl;
}栈的写法:可以直接用list。
7. 系统存在的性能瓶颈有哪些?
1. 慢查询:查询执行时间特别长,导致系统响应变慢。(10s以上)
探查方法:用SQL查询分析工具(例如mysqldumpslow)查看执行顺序。找到执行时间较长的查询。它可以找到慢查询所在的行,作为结果进行输出。
EXPLAIN SELECT * FROM 'user' 8. python列表、字典、元组的底层实现
列表是一个动态数组,如果超出当前容量,Python会分配一个更大的数组,将当前的元素复制到新数组中,也就是动态扩展。往列表里插入和删除操作,平均复杂度为On。
字典的底层实现是哈希表。每个键值对是存在哈希表中的槽中。键通过哈希转成一个索引,指向其值的存储位置。这种结构支持高效的插入、删除操作。字典的查找、插入删除的时间复杂度是O1.但在最坏的情况下(当所有的键映射到同一个槽的时候)退化到)On。Python的字典用了随机化来防止散列碰撞造成的性能下降。
元组的底层实现与列表相似,也是基于数组的,但是不可变的。它占用的空间比列表少。
9. 写一个简单的线性模型框架(分类模型)
import torch
import torch.nn as nn
import torch.nn.functional as F
from torch import optim
class Model(nn.Module):
def __init__(self,input_size,output_size):
super(Model,self).__init__()
self.fc1 = nn.Linear(input_size,input_size)
self.fc2 = nn.Linear(input_size,output_size)
def forward(self,x):
x = self.fc1(x)
x = self.fc2(x)
output = F.relu(x)
return output
input_size = 10
output_size = 1
model = Model(input_size,output_size)
criterion = nn.BCELoss() # 二分类交叉熵损失
optimizer = optim.SGD(model.parameters(), lr=0.01)
# data
input_data = torch.randn(100,10)
labels = torch.randint(0, 2, (100, 1)).type(torch.FloatTensor)
for epoch in range(100):
optimizer.zero_grad()
output = model(input_data)
loss = criterion(output,labels)
loss.backward()
optimizer.step()
print('epoch:{}, loss:{}'.format(epoch, loss))10. 返回前k个高频元素
和返回前k个最大值一样,都是用堆。其实可以先实现一个堆,感觉可能会考到
我这么写复杂了,用的优先队列,实际上也没有自己实现排序。先弄到字典里再弄到优先队列里。
class num():
def __init__(self,value,count):
self.val = value
self.count = count
def __lt__(self, other):
return self.count > other.count
if __name__ == '__main__':
for i in range(N):
nums.append(random.randint(0, N))
pq = queue.PriorityQueue()
freq_map = {}
for i in range(N):
if nums[i] in freq_map:
freq_map[nums[i]] +=1
else:
freq_map[nums[i]] = 1
for key,value in freq_map.items():
pq.put(num(key,value))
for i in range(10):
print(pq.get().val, pq.get().count)
python真逃课,可以直接对key,value排序:
keys = nums.keys()
keys.sort()
return [nums[key] for key in keys] 但是最好还是自己实现一下c++和python的堆排序。(未完待续)
11. 对数据做归一化的方式有哪些?
数据的标准化(normalization)就是指将原始各指标数据按比例缩放,去除数据的单位限制,将其转化为无量纲的纯数值,便于不同单位或量级的指标能够进行比较和加权。
归一化是标准化的一种,就是让他的结果在0-1之间。
(1)MinMax归一化 x* = ( x − min ) / ( max − min )
其中max为样本数据的最大值,min为样本数据的最小值。这种方法有个缺陷就是当有新数据加入时,可能导致max和min的变化,需要重新定义。
(2)Z-score归一化
这种方法给予原始数据的均值(mean)和标准差(standard deviation)进行数据的标准化。经过处理的数据符合标准正态分布,即均值为0,标准差为1,转化函数为:
x* = ( x − μ ) / σ
其中 μ为所有样本数据的均值,σ为所有样本数据的标准差。
(3)log函数转换是通过以10为底的log函数转换以实现归一下,具体方法如下:y=log10(x)/log10(max),max为样本数据最大值,并且所有的数据都要大于等于1。
12. 局部最小值与鞍点
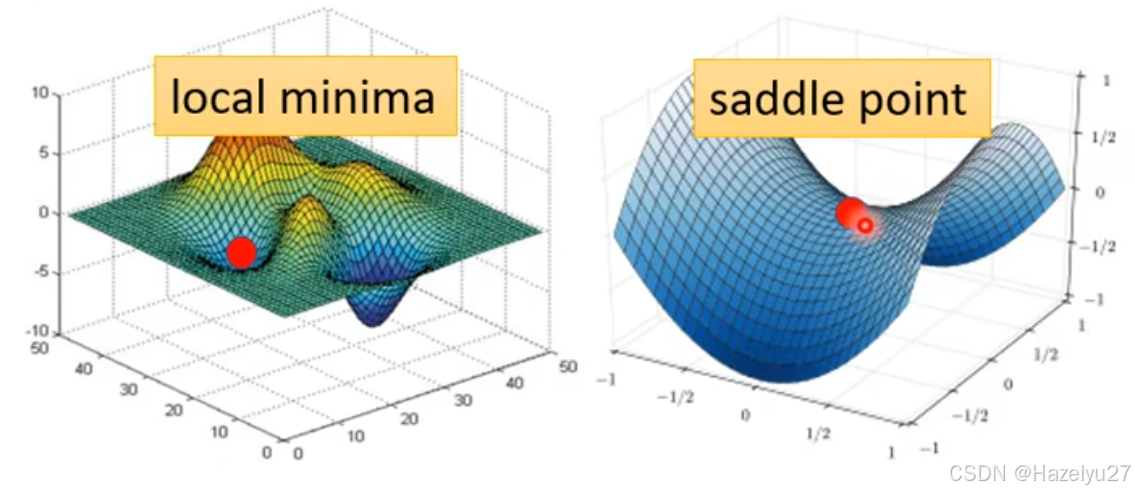
(来自李宏毅的机器学习课程)
为什么loss不下降了?因为梯度几乎趋于0.而梯度趋于0的地方除了局部最小值,还有鞍点。
局部最小值与鞍点的区别:局部最小值是前后左右都比它大,鞍点是前后比他大,左右比它小。
13. 有哪些数据降维的方式?
数据降维是针对非常长的数据,例如onehot向量的。
(1) PCA 主成分分析
PCA通过正交变换投影到一组新的坐标系统中,使得数据的任何投影的第一个坐标具有最大方差。第二个坐标具有第二大方差。
具体实现:
step1:标准化数据。step2:计算协方差矩阵,表示变量之间的相互关系。step3:计算特征值与特征向量。决定了数据的主成分方向。step4:选择主成分。一般选择特征值最大的前k个特征向量,这些向量构成了数据的新基,可以捕捉大部分的数据方差。选择多少个主成分常常依赖于特征值的大小,以及累计贡献率(通常设定一个阈值,如95%)。step5:转换到新的空间
(2)奇异值分解 SVD
奇异值分解适用于当一个矩阵是非方阵,无法求它的特征值和特征向量的时候,通过奇异值分解得到对称矩阵。
奇异值和特征值一样,在矩阵上由大到小排列。用k个奇异值就可以近似描述矩阵。在PCA里也可以用到奇异值分解。并且用奇异值分解比直接特征分解更快。只需要用到右奇异矩阵。
(3)线性判别分析 LDA
是一种监督学习的降维技术,主要用于分类问题。与 PCA 不同,LDA 旨在识别区分不同类别最有效的特征,从而最大化类间分离。因此,它不仅降维,还帮助提高分类性能。
实现方式是把数据投影到一个线上,让线上的数据同类距离最小,不同类距离最大。
(4)t-分布随机邻域嵌入(t-SNE)
t-SNE 是一种非线性降维技术,特别适用于将高维数据降维到二维或三维空间,以便进行可视化。t-SNE 通过概率分布在高维和低维空间中建立相似性,然后通过优化这些相似性来映射数据。
(5)自编码器
自编码器是一种利用神经网络进行降维的技术。它们通常由两部分组成:编码器和解码器。编码器的作用是将数据压缩成一个低维表示,而解码器则尝试从这个低维表示重构原始数据。自编码器特别适用于那些需要非线性降维方法的复杂数据集。
14. 写一个基础的ResNet模型
注意Residual Block的顺序是:conv+norm+relu,最后一个relu的输入是残差连接后的。
class ResidualBlock(nn.Module):
def __init__(self,in_channel,out_channel):
super(ResidualBlock).__init__()
self.conv1 = nn.Conv2d(in_channel,out_channel,kernel_size=3,stride=1,padding=1)
self.conv2 = nn.Conv2d(in_channel,out_channel,kernel_size=3,stride=1,padding=1)
self.bn1 = nn.BatchNorm2d(out_channel)
self.bn2 = nn.BatchNorm2d(out_channel)
self.relu = nn.ReLU()
def forward(self,x):
# 卷积+norm+relu
x = self.relu(self.bn1(self.conv1(x)))
# 第一次的x加上第二次的结果后再做Relu
x2 = self.bn2(self.conv2(x))
x += x2
out = self.relu(x)
return outResNet的写法(用于图像分类)在两个residual block之后加一个线性层。注意用view函数将数据压缩成1维(除了batch_size)。注意view函数的使用,-1表示其他的维度的数量是自适应的。
class ResNet(nn.Module):
def __init__(self,input_channel, num_classes):
super(ResNet).__init__()
channels = [16,32,64]
self.ResLayer1 = ResidualBlock(input_channel,channels[0])
self.ResLayer2 = ResidualBlock(channels[0],channels[1])
# pool的参数: kernel size, stride
self.pool = nn.MaxPool2d(2,2)
self.fc = nn.Linear(channels[1],num_classes)
def forward(self,x):
# x:(batch_size,w,h,channels)
x1 = self.pool(self.ResLayer1(x)) # x1:(batch_size,w/2,h/2,16)
x2 = self.pool(self.ResLayer2(x1)) # x2:(batch_size,w/4,h/4,32)
x3 = x2.view(x2.size(0),-1) # x3: (batch_size, w/4*h/4*32)
x4 = self.fc(x3) # x4: num_classes
return x4