计算机组成原理之定点运算

须知：

l 正数的补码为其原值，负数的补码为其每位取反最末位加1

l 二进制两位数相加最大为1，即0+0=0，0+1=1，1+1=10（10不是十而是一零）；则：

      01
+     01
————————
      10

一.加减法运算

1.补码加减法运算

加法：

[x]补+[y]补=[x+y]补 （mod 2^(n+1)）（即仅保留[x+y]补的n+1位有效位：1位符号，n位数字）

如：

例【1】 x=+1001，y=+0101，求x+y
解：
[x]补=01001，[y]补=00101

      [x]补       01001
+     [y]补       00101
————————————————————————
     [x+y]补      01110

则x+y=+1110（01110第一位0是符号位正，其余4位是真正的二进制值）

例【2】 x=+1011，y=-0101，求x+y
解：
[x]补=01011，[y]补=11011

则x+y=+0110（x和y都为4位数，100110为6位数，多出一位则舍弃多出的高位1）

例【3】 x=0.1011，y=-0.0101，求x+y
解：
[x]补=0.1011，[y]补=1.1011

则x+y=0.0110

减法：

[x]补-[y]补=[x]补+[-y]补

[-y]补=（[y]补包括符号位求反且最末位加1）

其余如加法

二．溢出判断

将符号位扩为相同的两位。如原数为+1011，原补码应为01011，现补码为001011.若两个这样的数相加减后两个符号位仍相同（即符号位为11或00），则无溢出，否则溢出（即符号位为10或01）

例【4】x=+1100，y=+1000，求x+y
解：
[x]补=001100，[y]补=001000

结果符号位为“01”，溢出。

三．定点乘法

1.原码乘法（即原码阵列乘法器）

符号位单独计算：x符号位⊕y符号位（⊕两边的值相同为0，不同为1.即1⊕0=1，1⊕1=0），数值位相乘

例【5】 设x=+15，y=-13，用带求补器的原码阵列乘法器求出乘积x * y

设最高位为符号位，则[x]原=01111，[y]原=11101

则最终结果的符号位为0⊕1=1

因符号位单独运算，则进行相乘的数值为|x|=1111，|y|=1101

乘法的结果加上符号位1得[x*y]原=11100011

转十进制值为-195

2.补码乘法（即补码阵列乘法器）

符号位单独计算：x符号位⊕y符号位，数值位先求补码，再进行原码相乘

例【6】 设x=-15，y=-13，用带求补器的补码阵列乘法器求出乘积x * y

设最高位为符号位，则

[x]补=10001，[y]补=10011

则最终结果的符号位为1⊕1=0

因符号位单独运算，则进行相乘的数值为|x|=1111，|y|=1101

乘法的结果加上符号位0得[x*y]原=01100011

转十进制值为+195

四．定点除法

1.不恢复余数法

x÷y形式的除法运算转化为[x]补 ± [y]补Y ± [y]补Y+1±……[y]补N形式的加减法运算，因为-[y]补=[-y]补，则可以转化为：[x]补 +
[y]补（或[-y]补）Y+[y]补（或[-y]补）Y+1+……[y]补（或[-y]补）N 形式的加法运算。

Y，Y+1……N为[y]补或[-y]补的位数，随累加的次数而逐渐加1至和x相同位数停止。而具体是加[y]补还是[-y]补，取决于前面累加的结果的符号是否和x一致，一致则这次加[-y]补，不一致则加[y]补。

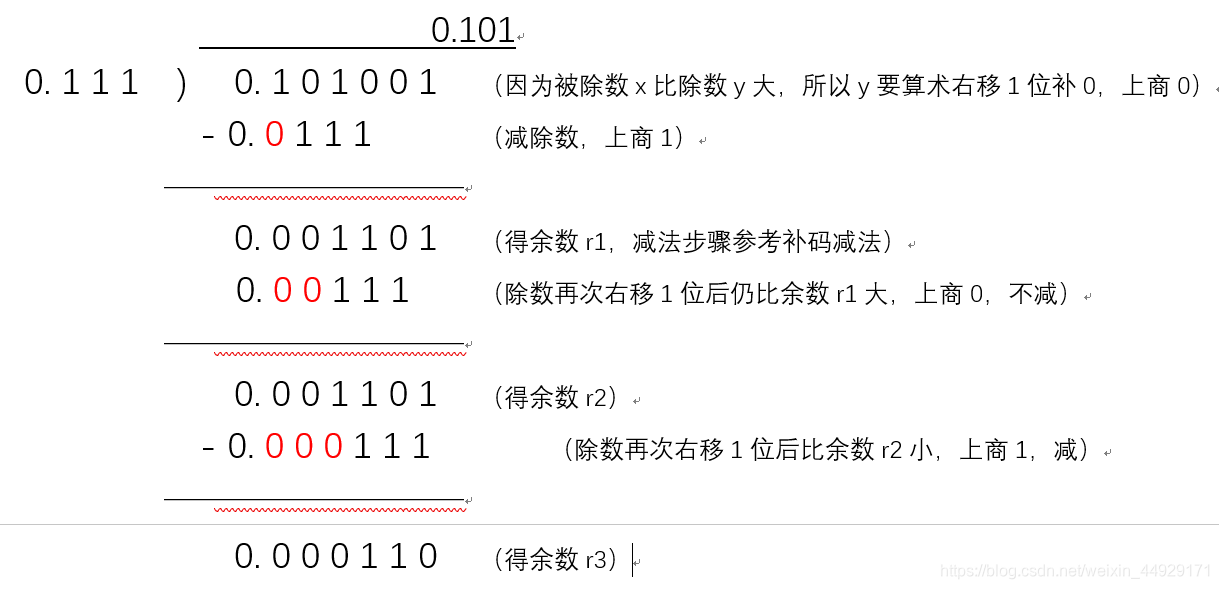
例【7】 x=0.101001，y=0.111，求x÷y

[x]补=0.101001，[y]补=0.111,[-y]补=1.001

则商取由上自下每次加减后的q = q4.q3 q2 q1 = 0.101

余数为累加后的结果r= 0.000110

2.恢复余数法

同样以例【7】为例，观察两种方法的不同

例【7】 x=0.101001，y=0.111，求x÷y

则x÷y商为0.101，余数r=0.000110