Latent Consistency Models: Synthesizing High-Resolution Images with Few-Step Inference
Latent Consistency Models 将 Consistency Models 扩展到了隐层、文生图扩散模型,提出了解 augmented PF-ODE 单阶段训练和 skipping-step 加速蒸馏训练。基于该方法训练的 LCM LoRA 是社区常用的通用加速模块。
前置知识:CM、SD 和 CFG
之前的文章介绍到,一致性模型 Consistency Models(CM)可以通过蒸馏训练,大大减少扩散模型采样生成所需的采样步数。具体来说,对预训练的生图模型进行蒸馏,训练得到一个一致性模型,该模型以任一中间时间步的噪声图作为输入的输出都是一致的,即有:
f
θ
(
x
t
,
t
)
=
f
θ
(
x
t
′
,
t
′
)
=
x
ϵ
∀
t
,
t
′
∈
[
ϵ
,
T
]
f_\theta(\mathbf{x}_t,t)=f_\theta(\mathbf{x}_{t'},t')=\mathbf{x}_\epsilon\quad\forall\ t,t'\in[\epsilon,T]
fθ(xt,t)=fθ(xt′,t′)=xϵ∀ t,t′∈[ϵ,T]
也就是说,CM 可以从 ODE 轨迹上任何一点直接一步生成出数据样本。这使得 CM 既可以追求极致效率,一步直接生图,也可以适当提高步数,采用(较少步的)多步生成,权衡采样速度和生图质量。
然而,CM 目前只是做在低分辨率的无条件生成上,而现实中的应用肯定要使用文本提示词等条件来控制生图,并且要追求更高的分辨率,更高的生图质量。回想之前在扩散模型(DM)刚出来之后,也是低分辨率的无条件生成,真正引爆图像生成应用的,是 Stable Diffusion(SD),也就是隐层扩散模型 Latent Diffusion Models (LDM)。SD/LDM 通过 VAE 来对像素空间的图像进行压缩和还原,从而使得扩散过程能够在维度较低的隐空间进行,提高了高分辨率大图的训练和推理效率。另外,SD 通过使用 Classifier-Free Guidance(CFG) 技术,并在在 UNet 中引入交叉注意力层,将文本提示词等条件注入到生图过程中,从而实现可控图像生成。
Latent Consistency Models (LCM)对 CM 做的事情正是类似于 LDM 对 DM 做的事情,即为其带来高分生成和可控生成的能力。从另一个角度来看,LCM 也是对 SD 的一种改进,将 CM 的加速采样能力嫁接到 SD 上。总之,LCM 是将 SD 的可控生成、高分生成与 CM 的加速采样能力结合起来。
LCM
LCM 将 CM 引用到隐层空间,两个核心的改进分别是 1. 通过解 augmented PF-ODE 实现单阶段的引导蒸馏 2. skipping-step 加速蒸馏训练。下面算法 1 就是 LCM 最核心的 LCD 算法。我们先过一遍 LCD 算法,然后介绍这两个改进。
- 首先,从图文对数据集 D \mathcal{D} D 中采样一个图文对 ( x , c ) (\mathbf{x},c) (x,c),并使用 VAE 的编码器提取图像的隐层特征 z = E ( x ) \mathbf{z}=E(\mathbf{x}) z=E(x)。采样一个时间步 n ∼ U [ 1 , N − k ] n\sim\mathcal{U}[1,N-k] n∼U[1,N−k] 和 CFG 权重系数 ω ∈ [ ω min , ω max ] \omega\in[\omega_\text{min},\omega_\text{max}] ω∈[ωmin,ωmax]。
- 然后,使用扩散模型的前向加噪公式向后 k k k 个时刻,得到 t n + k t_{n+k} tn+k 时刻的噪声图 z t n + k ∼ N ( α ( t n + k ) z ; σ 2 ( t n + k ) I ) \mathbf{z}_{t_{n+k}}\sim\mathcal{N}(\alpha(t_{n+k})\mathbf{z};\sigma^2(t_{n+k})\mathbf{I}) ztn+k∼N(α(tn+k)z;σ2(tn+k)I);
- 使用预训练的 SD 文生图模型和 ODE 求解器 Ψ ( ⋅ , ⋅ , ⋅ , ⋅ ) \Psi(\cdot,\cdot,\cdot,\cdot) Ψ(⋅,⋅,⋅,⋅) 向前 k k k 个时刻 t n t_n tn,且在 CFG scale 为 ω \omega ω 时的估计噪声图 z ^ t n Ψ , ω ← z t n + k + ( 1 + ω ) Ψ ( z t n + k , t n + k , t n , c ) − ω Ψ ( z t n + k , t n + k , t n , ∅ ) \hat{\mathbf{z}}^{\Psi,\omega}_{t_n}\leftarrow\mathbf{z}_{t_{n+k}}+(1+\omega)\Psi(\mathbf{z}_{t_{n+k}},t_{n+k},t_n,c)-\omega\Psi(\mathbf{z}_{t_{n+k}},t_{n+k},t_n,\emptyset) z^tnΨ,ω←ztn+k+(1+ω)Ψ(ztn+k,tn+k,tn,c)−ωΨ(ztn+k,tn+k,tn,∅);
- 计算一致性模型 f θ f_\theta fθ 关于 t n + k t_{n+k} tn+k 和 t n t_n tn 两个时刻在 CFG scale 为 ω \omega ω 下的输出,并计算二者的差异距离,即为 LCD 损失 L ( θ , θ − ; Ψ ) ← d ( f θ ( z t n + k , ω , c , t n + k ) , f θ − ( z ^ t n Ψ , ω , ω , c , t n ) \mathcal{L}(\theta,\theta^-;\Psi)\leftarrow d(f_\theta(\mathbf{z}_{t_{n+k}},\omega,c,t_{n+k}),f_{\theta^-}(\hat{z}_{t_n}^{\Psi,\omega},\omega,c,t_n) L(θ,θ−;Ψ)←d(fθ(ztn+k,ω,c,tn+k),fθ−(z^tnΨ,ω,ω,c,tn)
- 求损失的梯度,更新参数 θ ← θ − η ∇ θ L ( θ , θ − ) \theta\leftarrow\theta-\eta\nabla_\theta\mathcal{L}(\theta,\theta^-) θ←θ−η∇θL(θ,θ−);
- EMA 更新参数 θ − ← stopgrad ( μ θ − + ( 1 − μ ) θ ) \theta^-\leftarrow\text{stopgrad}(\mu\theta^-+(1-\mu)\theta) θ−←stopgrad(μθ−+(1−μ)θ)
注:因为是从连续时间 ODE 考虑,然后再进行离散化,所以说的是 t n + k t_{n+k} tn+k 时刻,而不是第 n + k n+k n+k 时间步。
上述过程中标红的两处这是对应着 LCM 的两个改进。
- 首先,在第 4 步,因为是(文本)条件生成模型,因此将 CFG scale 的值 ω \omega ω 也告诉模型,作为一种额外条件,这就是所谓的 augmented PF-ODE。这就实现了单阶段的蒸馏训练。
- 另外,在 2 步,不同于 CM 中每次构造的都是相邻时刻的输入对 ( x ^ n , x n + 1 ) (\hat{\mathbf{x}}_{n},\mathbf{x_{n+1}}) (x^n,xn+1),LCM 中使用一些可跳步的采样器(如 DDIM,DPM Solver 等),来构造相隔 k k k 个时刻的输入对 ( z ^ n , z n + k ) (\hat{\mathbf{z}}_{n},\mathbf{z_{n+k}}) (z^n,zn+k)。这就是所谓的 skipping-step,这样可以避免相邻时间步模型输出差异太小,加速蒸馏训练。
LCM-LoRA
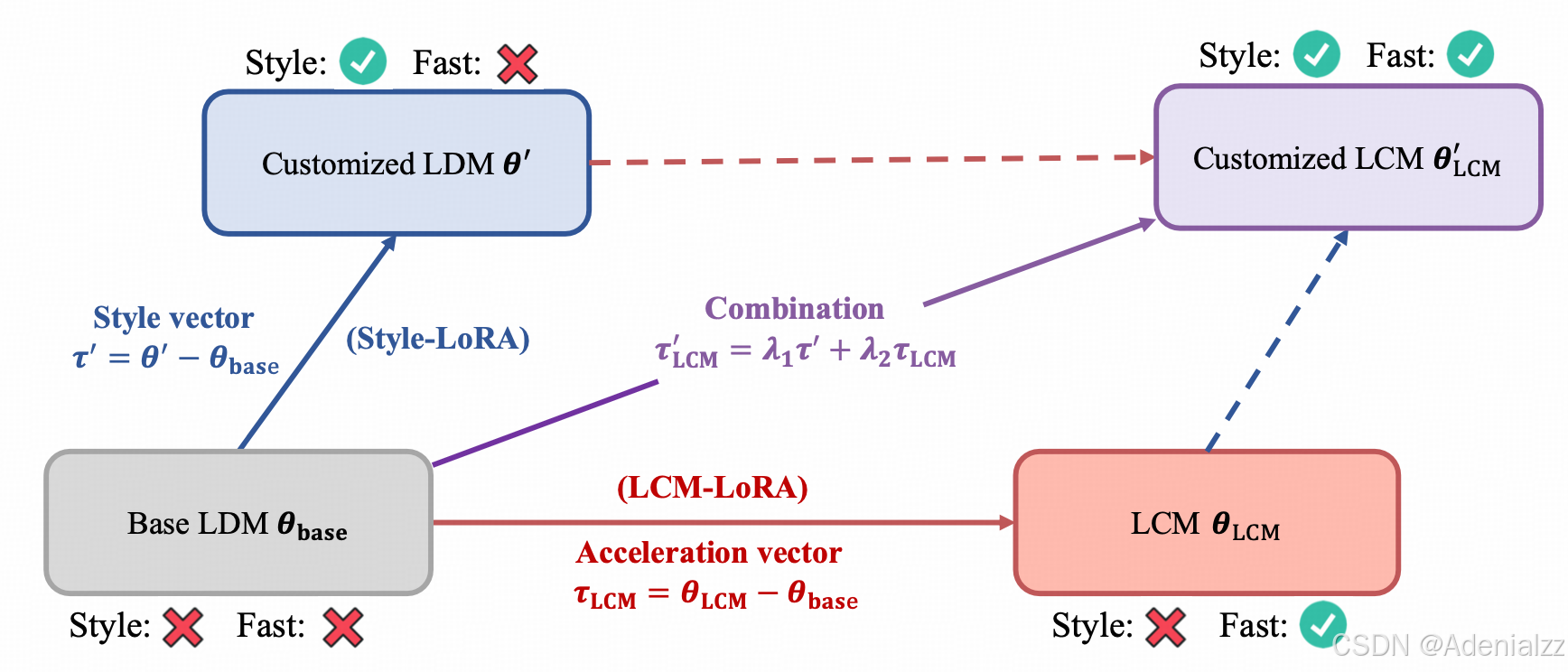
既然 LCM 是在预训练的 SD 上进行微调,那我们当然也可以使用 LoRA 这种高效的微调方式。并且,作者还发现,LCM LoRA 可以作为一个通用的、即插即用的提升生成速度的组件,训练一次,即可以融合到任何的 SD 模型中。并且,可以与其他的风格 LoRA 进行融合,彼此的作用不会相互影响,从而得到既有定制化风格,又可以快速采样生图的模型。
总结
LCM 将 CM 拓展到了隐层文生图模型,实现了对 SD 的加速采样,LCM LoRA 更是火爆社区,成为最常用的 SD 加速采样模块之一。