前言

从文件中获取数据，判断数据是否服从正态分布或者近似服从正态分布。

正态分布：也称“常态分布”，又名高斯分布（Gaussian distribution）
若随机变量X服从一个数学期望为μ、方差为σ2的正态分布，记为N(μ，σ2)。
其概率密度函数为正态分布的期望值μ决定了其位置，其标准差σ决定了分布的幅度。
当μ = 0,σ = 1时的正态分布是标准正态分布。

判断方法

• KS检验
  基于累计分布函数的，用于检验一个分布是否符合某种理论分布或比较两个经验分布是否有显著差异。

kstest方法：参数分别是：待检验的数据，检验方法（这里设置成norm正态分布），均值与标准差
结果返回两个值：statistic → D值，pvalue → P值
p值大于0.05，为正态分布
H0:样本符合
H1:样本不符合
如何p>0.05接受H0 ,反之

#导入scipy模块
from scipy import stats
import pandas as pd
data = pd.read_excel(r'sale.xls', index_col = False) #读取数据
u = data[u'销量'].mean()  # 计算均值
std = data[u'销量'].std()  # 计算标准差
stats.kstest(data[u'销量'], 'norm', (u, std))

结果展示

KstestResult(statistic=0.16962184456795837, pvalue=1.5900252683896546e-05)

pvalue < 0.05,不符合

• 画图观测

#导入模块
import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
%matplotlib inline
#导入scipy模块
from scipy import stats

data = pd.read_excel(r'sale.xls', index_col = False) #读取数据

# 构造一组随机数据
s = data[u'销量']

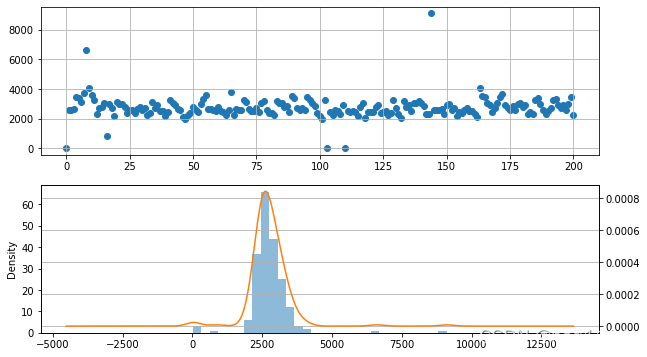
# 画散点图和直方图
fig = plt.figure(figsize = (10,6))
ax1 = fig.add_subplot(2,1,1)  # 创建子图1
ax1.scatter(s.index, s.values)
plt.grid()

ax2 = fig.add_subplot(2,1,2)  # 创建子图2
s.hist(bins=30,alpha = 0.5,ax = ax2)
s.plot(kind = 'kde', secondary_y=True,ax = ax2)
plt.grid()

从图中观察，不符合，但近似符合。

总结

有些时候需要数据为正态分布才能进行研究，所以要先对数据进行判断一下。如果不满足正态分布，可以对数据进行处理分析。
采用方法为log 取对数，之后再对其进行分析。

data[u'销量'] = data['销量'].apply(lambda x: np.log(x))

针对具体应用场景，近似正态分布也可以采用正态分布相关的方法分析。