一、堆的基本概念

堆是一种非线性结构，可以看作是一棵二叉树，也可以表示为一个数组。简而言之，堆就是利用完全二叉树的结构来维护的一维数组。

堆分为大顶堆和小顶堆两种类型：

• 大顶堆：每个节点的值都大于或等于其左右孩子节点的值。
• 小顶堆：每个节点的值都小于或等于其左右孩子节点的值。

在排序算法中：

• 升序排序使用大顶堆。
• 降序排序使用小顶堆。

对于Top K问题，也可以用堆来实现：

• 找最大的 K 个元素：使用小顶堆。
• 找最小的 K 个元素：使用大顶堆。

二、大顶堆的构建过程

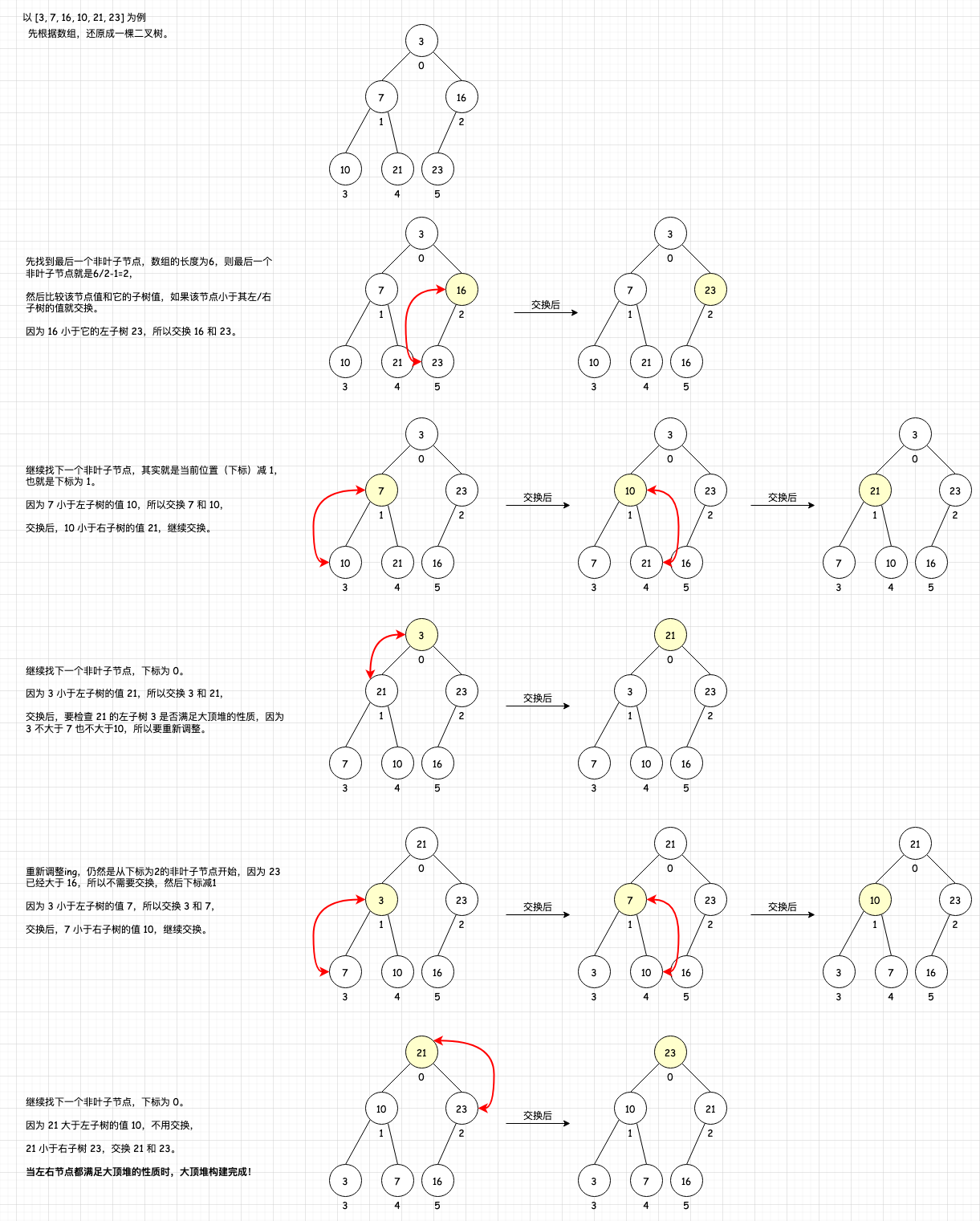
大顶堆的构建过程从最后一个非叶子节点开始，从下往上进行调整。

如何找到最后一个非叶子节点？
假设用数组表示待排序的序列，则最后一个非叶子节点的位置是：数组长度/2 - 1。
例如，若数组长度为9，则最后一个非叶子节点的位置是：9/2 - 1 = 3。

调整过程：

1. 比较当前节点与左子树的值：
   • 如果当前节点小于左子树的值，交换两者的位置。
   • 交换后，检查左子树是否满足大顶堆的性质，不满足则重新调整子树结构。
2. 比较当前节点与右子树的值：
   • 如果当前节点小于右子树的值，交换两者的位置。
   • 交换后，检查右子树是否满足大顶堆的性质，不满足则重新调整子树结构。

当无需交换时，大顶堆的构建完成。

图解：以数组 [3, 7, 16, 10, 21, 23] 为例，展示大顶堆的构建过程。

三、大顶堆的排序过程

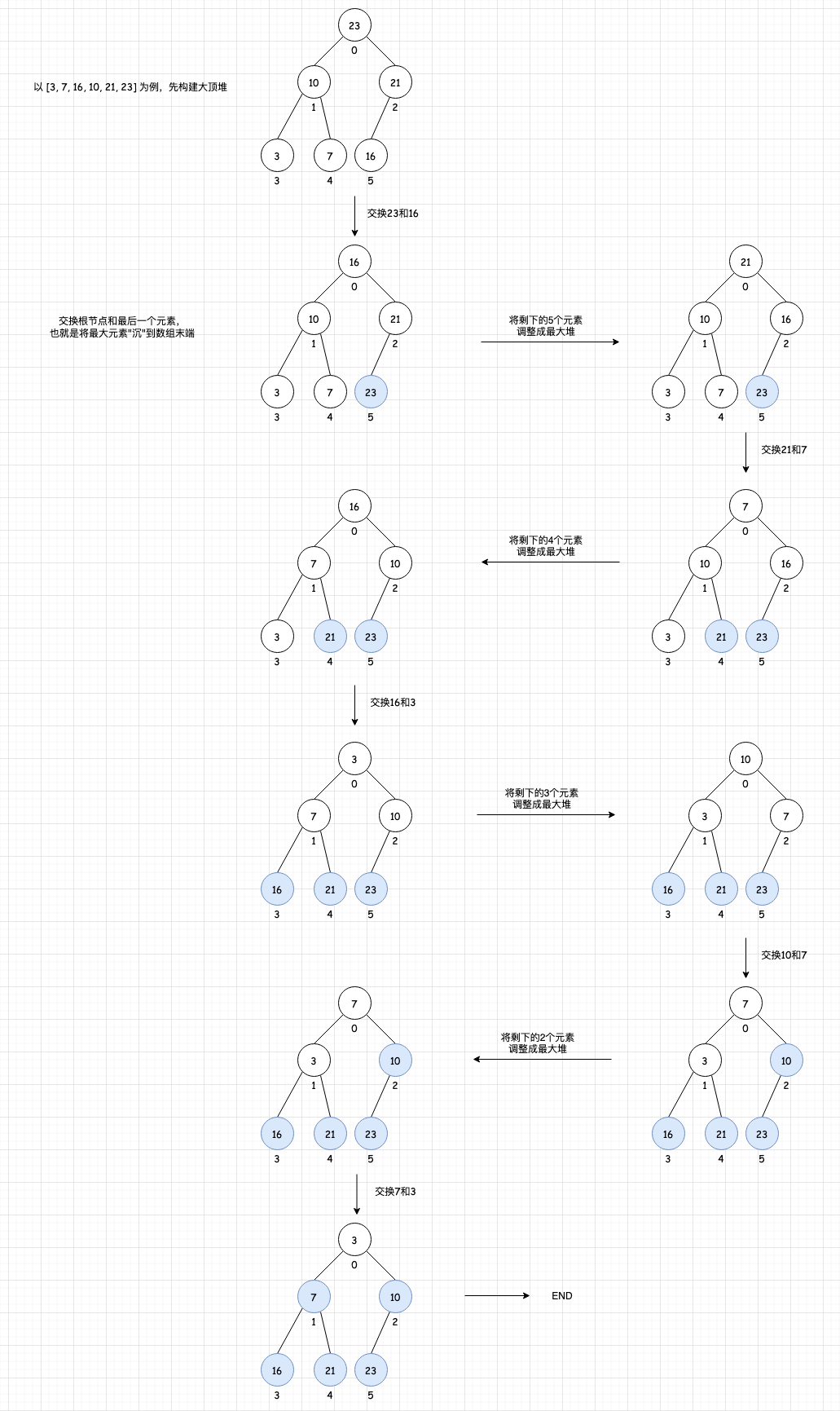
排序过程概括如下：

1. 构建大顶堆：将无序序列构造成大顶堆。
2. 交换根节点与末尾元素：最大值（堆顶）与末尾元素交换，此时末尾元素为最大值。
3. 重新构建大顶堆：将剩余的 n-1 个元素重新构建成大顶堆。
4. 重复步骤2和3：直到整个序列排序完成。

总结： 以上过程反复执行，最终将一个无序的数组排序为一个有序序列。

原文链接：https://www.cnblogs.com/sunshineliulu/p/12995910.html​​​​​​