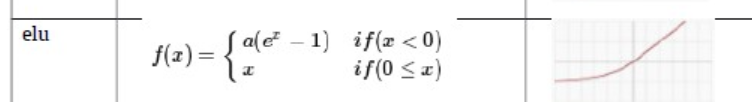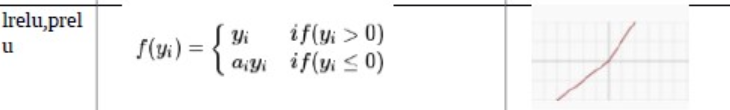PyTorch中文文档阅读笔记-day1

写在开头（重复的）

1.课程来源：torch中文教程1.7版.
torch中文文档.
2.笔记目的：个人学习+增强记忆+方便回顾
3.时间：2021年4月29日
4.仅作为个人笔记，如有需要请务必按照链接阅读文档

—以下正文—

一、torch.nn到底是干嘛的

1.torch.nn库中包含一系列函数和类。torch.nn.functional模块包含torch.nn库中的所有函数，通常按照惯例将其导入到名称空间F中，这样可以方便的调用torch.nn中所有函数。除了广泛的损失和激活函数外，您还会在这里找到一些方便的函数来创建神经网络，例如合并函数。还有一些用于进行卷积，线性层等的函数。

import torch.nn.functional as F

2.接下来，我们将使用nn.Module和nn.Parameter进行更清晰，更简洁的训练循环。我们将nn.Module子类化（它本身是一个类并且能够跟踪状态）。在这种情况下，我们要创建一个类，该类包含前进步骤的权重，偏置和方法。 nn.Module具有许多我们将要使用的属性和方法（例如.parameters()和.zero_grad()）。

随意定义一个线性变换

from torch import nn
import torch.nn.functional as F
# 下面用到的xb变量是一个batch=64的图组
loss_func = F.cross_entropy

class Mnist_Logistic(nn.Module):
    def __init__(self):
        super().__init__()  #通过父类的初始化进行初始换
        self.weights = nn.Parameter(torch.randn(784, 10) / math.sqrt(784))  #自己设置的随机的w
        self.bias = nn.Parameter(torch.zeros(10)) #全为零的b

    def forward(self, xb):
        return xb @ self.weights + self.bias
#由于这是类，不要忘记初始化
model = Mnist_Logistic()

#虽然是个对象，却可以像调用函数一样计算损失。 请注意，nn.Module对象的使用就好像它们是函数一样（即，它们是可调用的），但是在后台 Pytorch 会自动调用我们的forward方法。

print(loss_func(model(xb), yb))
#这一步输出为：tensor(2.3903, grad_fn=<NllLossBackward>)
#由输出可知，我们知识像函数调用一样modle(xb),他就在后台完成了forward方法，并且该类里面存了一大堆梯度参数。

下面非常友好的一点在了，在不用nn.Module类的情况下，我们将不得不反复书写权重的梯度下降和已经用完的梯度清零，下面代码段展示的是1层情况，想象一下你有18层、21层要清理。。。。

with torch.no_grad():
    weights -= weights.grad * lr
    bias -= bias.grad * lr
    weights.grad.zero_()
    bias.grad.zero_()

但是使用nn.Module类后，可以用如下方法批量清理

with torch.no_grad():
    for p in model.parameters(): 
        p -= p.grad * lr
    model.zero_grad()

4.让我们总结一下我们所看到的：
- 4.1torch.nn
  - Module：创建一个行为类似于函数的可调用对象，但也可以包含状态（例如神经网络层权重）。它知道其中包含的 Parameter ，并且可以将其所有坡度归零，遍历它们以进行权重更新等。
  - Parameter：张量的包装器，用于告知 Module 具有在反向传播期间需要更新的权重。仅更新具有require_grad属性集的张量
  - functional：一个模块（通常按照惯例导入到 F 名称空间中），其中包含激活函数，损失函数等。以及卷积和线性层等层的无状态版本。
- 4.2torch.optim：包含诸如 SGD 的优化程序，这些优化程序在后退步骤
- 4.3Dataset 中更新 Parameter 的权重。具有 len 和 getitem 的对象，包括 Pytorch 提供的类，例如 TensorDataset
- 4.4DataLoader：获取任何 Dataset 并创建一个迭代器，该迭代器返回批量数据。

二、torch.nn包

（一）容器

1.Containers（容器）：
- class torch.nn.Module
- class torch.nn.Sequential(* args)
- class torch.nn.ParameterList(parameters=None)
- class torch.nn.ModuleList(modules=None)
2.class torch.nn.Module上的register_backward_hook(hook)和register_forward_hook(hook)：非常有趣，详见https://blog.csdn.net/u011995719/article/details/97752853的讲解
3.class torch.nn.Module上的zero_grad()将module中的所有模型参数的梯度设置为0。可以说是非常常用了。
4.class torch.nn.Sequential(* args)，从使用角度介绍

import torch.nn as nn
model = nn.Sequential(
          nn.Conv2d(1,20,5),
          nn.ReLU(),
          nn.Conv2d(20,64,5),
          nn.ReLU()
        )

就是这么个容器。

（二）卷积层

1.卷积层的模板：
- class torch.nn.Conv1d(in_channels, out_channels, kernel_size, stride=1, padding=0, dilation=1, groups=1, bias=True)
- class torch.nn.Conv2d(in_channels, out_channels, kernel_size, stride=1, padding=0, dilation=1, groups=1, bias=True)
- class torch.nn.Conv3d(in_channels, out_channels, kernel_size, stride=1, padding=0, dilation=1, groups=1, bias=True)
- class torch.nn.ConvTranspose1d(in_channels, out_channels, kernel_size, stride=1, padding=0, output_padding=0, groups=1, bias=True)论文中，可以称为fractionally-strided convolutions，也有的称为deconvolutions,但是我不建议大家用后一个，因为这个实际操作并不是去卷积。这就是上采样的一种方法，可以但不准确和不推荐的称之为逆卷积。
- class torch.nn.ConvTranspose2d(in_channels, out_channels, kernel_size, stride=1, padding=0, output_padding=0, groups=1, bias=True)同上
- torch.nn.ConvTranspose3d(in_channels, out_channels, kernel_size, stride=1, padding=0, output_padding=0, groups=1, bias=True)

（三）池化层

1.池化层模板
- class torch.nn.MaxPool1d(kernel_size, stride=None, padding=0, dilation=1, return_indices=False, ceil_mode=False)
- class torch.nn.MaxPool2d(kernel_size, stride=None, padding=0, dilation=1, return_indices=False, ceil_mode=False)注意这里的kernel_size既可以用一个int表示，也可以用tuple数组表示。int则代表一个n*n的正方形池化视野，数组则代表一个（n,m）的非正方形的池化视野。
- class torch.nn.MaxPool3d(kernel_size, stride=None, padding=0, dilation=1, return_indices=False, ceil_mode=False)
- class torch.nn.MaxUnpool1d(kernel_size, stride=None, padding=0)空位填零
- class torch.nn.MaxUnpool2d(kernel_size, stride=None, padding=0)同上
- class torch.nn.MaxUnpool3d(kernel_size, stride=None, padding=0)同上
- class torch.nn.AvgPool1d(kernel_size, stride=None, padding=0, ceil_mode=False, count_include_pad=True)平均池化
- class torch.nn.AvgPool2d(kernel_size, stride=None, padding=0, ceil_mode=False, count_include_pad=True)平均池化
- class torch.nn.AvgPool3d(kernel_size, stride=None)平均池化
- class torch.nn.FractionalMaxPool2d(kernel_size, output_size=None, output_ratio=None, return_indices=False, _random_samples=None)分数最大池与常规最大池化略有不同.在常规最大池化中,通过获取集合中较小N×N子部分的最大值(通常为2x2)来缩小输入集的大小,并尝试将集合减少N倍,其中N是整数.正如您可能从“分数”一词所预期的那样,分数最大池化意味着整体缩减比率N不必是整数。
- class torch.nn.LPPool2d(norm_type, kernel_size, stride=None, ceil_mode=False)供2维的幂平均池化操作，其计算公式为f(x)=pow(sum(X,p),1/p)
- class torch.nn.AdaptiveMaxPool1d(output_size, return_indices=False)对输入信号，提供1维的自适应最大池化操作对于任何输入大小的输入，可以将输出尺寸指定为H，但是输入和输出特征的数目不会变化。
- class torch.nn.AdaptiveMaxPool2d(output_size, return_indices=False)对输入信号，提供2维的自适应最大池化操作对于任何输入大小的输入，可以将输出尺寸指定为H*W，但是输入和输出特征的数目不会变化。
- class torch.nn.AdaptiveAvgPool1d(output_size)
- class torch.nn.AdaptiveAvgPool2d(output_size)

（三）Non-Linear Activations（SS非线性激活层）

1.分类：
- class torch.nn.ReLU(inplace=False)
- class torch.nn.ReLU6(inplace=False) 运算如下函数*{ReLU6}(x) = min(max(0,x), 6)* 。具体使用情况：在Mobile v1里面使用ReLU6，ReLU6就是普通的ReLU但是限制最大输出值为6（对输出值做clip），这是为了在移动端设备float16的低精度的时候，也能有很好的数值分辨率，如果对ReLU的激活范围不加限制，输出范围为0到正无穷，如果激活值非常大，分布在一个很大的范围内，则低精度的float16无法很好地精确描述如此大范围的数值，带来精度损失。
- class torch.nn.ELU(alpha=1.0, inplace=False) 运算如下函数f(x) = max(0,x) + min(0, alpha * (e^x - 1))
- class torch.nn.PReLU(num_parameters=1, init=0.25) 运算如下函数PReLU(x) = max(0,x) + a * min(0,x) （PS：a为可学习参数）
- class torch.nn.LeakyReLU(negative_slope=0.01, inplace=False)
- class torch.nn.Threshold(threshold, value, inplace=False) 具体函数为y=x,if x>=threshold 或者 y=value,if x<threshold。threshold：阈值。value：输入值小于阈值则会被value代替。
- class torch.nn.Hardtanh(min_value=-1, max_value=1, inplace=False) 具体函数f(x)=+1,if x>1; f(x)=−1,if x<−1; f(x)=x,otherwise。min_value和 max_value可设置。
- class torch.nn.Sigmoid（）无参数
- class torch.nn.Tanh（）无参数
- class torch.nn.LogSigmoid（）无参数
- class torch.nn.Softplus(beta=1, threshold=20) 具体函数为：f(x)=1beta∗log(1+e(beta∗xi))。图像上看，Softplus函数是ReLU函数的平滑逼近，Softplus函数可以使得输出值限定为正数。
- class torch.nn.Softsign走势完全近似于tanh，但是稍稍平滑。
- class torch.nn.Softshrink(lambd=0.5) SS没看出有有啥优越性。
- class torch.nn.Softmin（）无参数。具体公式不展示，效果是对n维输入张量运用Softmin函数，将张量的每个元素缩放到（0,1）区间且和为1，真实值越小，在softmin之后在1中的占比就越大。使softmax的一种类似思想，但不知具体是否好用。
- class torch.nn.Softmax（）无参数。对n维输入张量运用Softmax函数，将张量的每个元素缩放到（0,1）区间且和为1。越大值，在1中占比越大。
- class torch.nn.LogSoftmax（）无参数。

（四）Normalization layers（SS正规化层）

1.分类：
- class torch.nn.BatchNorm1d(num_features, eps=1e-05, momentum=0.1, affine=True) 对小批量(mini-batch)的2d或3d输入进行批标准化(Batch Normalization)操作

>>> # With Learnable Parameters
>>> m = nn.BatchNorm1d(100)
>>> # Without Learnable Parameters
>>> m = nn.BatchNorm1d(100, affine=False)
>>> input = autograd.Variable(torch.randn(20, 100)) #注意100的位置
>>> output = m(input)

class torch.nn.BatchNorm2d(num_features, eps=1e-05, momentum=0.1, affine=True)对小批量(mini-batch)3d数据组成的4d输入进行批标准化(Batch Normalization)操作

>>> # With Learnable Parameters
>>> m = nn.BatchNorm2d(100)
>>> # Without Learnable Parameters
>>> m = nn.BatchNorm2d(100, affine=False)
>>> input = autograd.Variable(torch.randn(20, 100, 35, 45))#注意100的位置
>>> output = m(input)

class torch.nn.BatchNorm3d(num_features, eps=1e-05, momentum=0.1, affine=True)对小批量(mini-batch)4d数据组成的5d输入进行批标准化(Batch Normalization)操作

>>> # With Learnable Parameters
>>> m = nn.BatchNorm3d(100)
>>> # Without Learnable Parameters
>>> m = nn.BatchNorm3d(100, affine=False)
>>> input = autograd.Variable(torch.randn(20, 100, 35, 45, 10))#注意100的位置
>>> output = m(input)

（五）Recurrent layers（循环神经网络里用到的）

（六）Linear layers（线性层（SS全连接层））

1.class torch.nn.Linear(in_features, out_features, bias=True)比如在处理1281283，最后分10类时，参数就用in_features=49152, out_features=10。

（七）Dropout layers（dropout层）

1.class torch.nn.Dropout(p=0.5, inplace=False) 这里有个巨大的坑。dropout总是不起作用怎么办
class torch.nn.Dropout2d(p=0.5, inplace=False)体会两者区别
class torch.nn.Dropout3d(p=0.5, inplace=False)

（七）Sparse layers

（八）Distance functions（距离函数）

1.class torch.nn.PairwiseDistance(p=2, eps=1e-06)

（九）Loss functions

1.所有损失函数的使用方法都如下

criterion = LossCriterion() #构造函数有自己的参数
......
......
loss = criterion(x, y) #调用标准时也有参数

2.class torch.nn.L1Loss(size_average=True)衡量差的绝对值的平均值。（PS：注意，上面参数这是实例化时使用的，实例化后的loss函数要传入传入x和y）
3.class torch.nn.MSELoss(size_average=True) 。具体函数：loss(x,y)=1/n∑(xi−yi)2。这不是方差！注意y也在随着i变动。
4.class torch.nn.CrossEntropyLoss(weight=None, size_average=True) 这个很常用。它整合结合了nn.LogSoftmax()和nn.NLLLoss()两个函数，既实现了自动的标准化和计算交叉熵。
5.class torch.nn.NLLLoss(weight=None, size_average=True)负对数损失，上面整合了。
6.class torch.nn.NLLLoss2d(weight=None, size_average=True)
7.class torch.nn.KLDivLoss(weight=None, size_average=True)计算KL散度。
。。。。。还有一大堆乱七八糟的损失函数，具体使用时再看，没有示例根本看不懂。

（十）Vision layers（上采样层）

1.class torch.nn.PixelShuffle(upscale_factor)具体使用方法
2.class torch.nn.UpsamplingNearest2d(size=None, scale_factor=None)2D近邻采样
3.class torch.nn.UpsamplingBilinear2d(size=None, scale_factor=None)插值上采样，具体效果如代码所示。

>>> inp
Variable containing:
(0 ,0 ,.,.) =
  1  2
  3  4
[torch.FloatTensor of size 1x1x2x2]

>>> m = nn.UpsamplingBilinear2d(scale_factor=2)
>>> m(inp)
Variable containing:
(0 ,0 ,.,.) =
  1.0000  1.3333  1.6667  2.0000
  1.6667  2.0000  2.3333  2.6667
  2.3333  2.6667  3.0000  3.3333
  3.0000  3.3333  3.6667  4.0000
[torch.FloatTensor of size 1x1x4x4]

二、怎么又冒出个torch.nn.functional

作者：有糖吃可好
链接：https://www.zhihu.com/question/66782101/answer/579393790
来源：知乎
著作权归作者所有。商业转载请联系作者获得授权，非商业转载请注明出处。

1.两者的相同之处：
- nn.Xxx和nn.functional.xxx的实际功能是相同的，即nn.Conv2d和nn.functional.conv2d 都是进行卷积，nn.Dropout 和nn.functional.dropout都是进行dropout，。。。。。；
- 运行效率也是近乎相同。
2.nn.functional.xxx是函数接口，而nn.Xxx是nn.functional.xxx的类封装，并且nn.Xxx都继承于一个共同祖先nn.Module。这一点导致nn.Xxx除了具有nn.functional.xxx功能之外，内部附带了nn.Module相关的属性和方法，例如train(), eval(),load_state_dict, state_dict 等。
3.两者的差别之处：
- 两者的调用方式不同。nn.Xxx 需要先实例化并传入参数，然后以函数调用的方式调用实例化的对象并传入输入数据。

inputs = torch.rand(64, 3, 244, 244)
conv = nn.Conv2d(in_channels=3, out_channels=64, kernel_size=3, padding=1)
out = conv(inputs)

nn.functional.xxx同时传入输入数据和weight, bias等其他参数。

weight = torch.rand(64,3,3,3)
bias = torch.rand(64) 
out = nn.functional.conv2d(inputs, weight, bias, padding=1)

nn.Xxx继承于nn.Module，能够很好的与nn.Sequential结合使用，而nn.functional.xxx无法与nn.Sequential结合使用。

fm_layer = nn.Sequential(
            nn.Conv2d(3, 64, kernel_size=3, padding=1),
            nn.BatchNorm2d(num_features=64),
            nn.ReLU(),
            nn.MaxPool2d(kernel_size=2),
            nn.Dropout(0.2)
  )

nn.Xxx不需要你自己定义和管理weight；而nn.functional.xxx需要你自己定义weight，每次调用的时候都需要手动传入weight, 不利于代码复用。使用nn.Xxx定义一个CNN 。

class CNN(nn.Module):
    
    
    def __init__(self):
        super(CNN, self).__init__()
        
        self.cnn1 = nn.Conv2d(in_channels=1,  out_channels=16, kernel_size=5,padding=0)
        self.relu1 = nn.ReLU()
        self.maxpool1 = nn.MaxPool2d(kernel_size=2)
        
        self.cnn2 = nn.Conv2d(in_channels=16, out_channels=32, kernel_size=5,  padding=0)
        self.relu2 = nn.ReLU()
        self.maxpool2 = nn.MaxPool2d(kernel_size=2)
        
        self.linear1 = nn.Linear(4 * 4 * 32, 10)
        
    def forward(self, x):
        x = x.view(x.size(0), -1)
        out = self.maxpool1(self.relu1(self.cnn1(x)))
        out = self.maxpool2(self.relu2(self.cnn2(out)))
        out = self.linear1(out.view(x.size(0), -1))
        return out

使用nn.function.xxx定义一个与上面相同的CNN。

class CNN(nn.Module):
    
    
    def __init__(self):
        super(CNN, self).__init__()
        
        self.cnn1_weight = nn.Parameter(torch.rand(16, 1, 5, 5))
        self.bias1_weight = nn.Parameter(torch.rand(16))
        
        self.cnn2_weight = nn.Parameter(torch.rand(32, 16, 5, 5))
        self.bias2_weight = nn.Parameter(torch.rand(32))
        
        self.linear1_weight = nn.Parameter(torch.rand(4 * 4 * 32, 10))
        self.bias3_weight = nn.Parameter(torch.rand(10))
        
    def forward(self, x):
        x = x.view(x.size(0), -1)
        out = F.conv2d(x, self.cnn1_weight, self.bias1_weight)
        out = F.relu(out)
        out = F.max_pool2d(out)
        
        out = F.conv2d(x, self.cnn2_weight, self.bias2_weight)
        out = F.relu(out)
        out = F.max_pool2d(out)
        
        out = F.linear(x, self.linear1_weight, self.bias3_weight)
        return out

4.上面两种定义方式得到CNN功能都是相同的，至于喜欢哪一种方式，是个人口味问题，但PyTorch官方推荐：具有学习参数的（例如，conv2d, linear, batch_norm)采用nn.Xxx方式，没有学习参数的（例如，maxpool, loss func, activation func）等根据个人选择使用nn.functional.xxx或者nn.Xxx方式。但关于dropout，个人强烈推荐使用nn.Xxx方式，因为一般情况下只有训练阶段才进行dropout，在eval阶段都不会进行dropout。使用nn.Xxx方式定义dropout，在调用model.eval()之后，model中所有的dropout layer都关闭，但以nn.function.dropout方式定义dropout，在调用model.eval()之后并不能关闭dropout。

class Model1(nn.Module):
    
    def __init__(self):
        super(Model1, self).__init__()
        self.dropout = nn.Dropout(0.5)
        
    def forward(self, x):
        return self.dropout(x)
    
    
class Model2(nn.Module):

    def __init__(self):
        super(Model2, self).__init__()

    def forward(self, x):
        return F.dropout(x)
    

m1 = Model1()
m2 = Model2()
inputs = torch.rand(10)
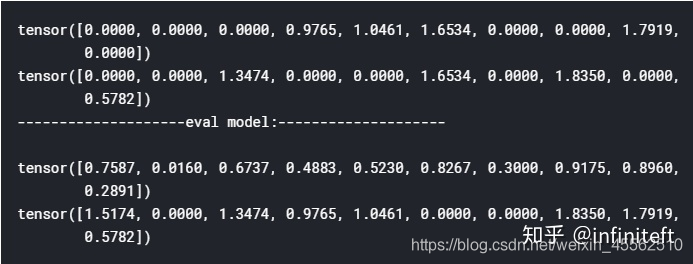
print(m1(inputs))
print(m2(inputs))
print(20 * '-' + "eval model:" + 20 * '-' + '\r\n')
m1.eval()
m2.eval()
print(m1(inputs))
print(m2(inputs))

输出：
在这里插入图片描述

从上面输出可以看出m2调用了eval之后，dropout照样还在正常工作。当然如果你有强烈愿望坚持使用nn.functional.dropout，也可以采用下面方式来补救。

 class Model3(nn.Module):

    def __init__(self):
        super(Model3, self).__init__()

    def forward(self, x):
        return F.dropout(x, training=self.training)

5.什么时候使用nn.functional.xxx，什么时候使用nn.Xxx?
- 这个问题依赖于你要解决你问题的复杂度和个人风格喜好。在nn.Xxx不能满足你的功能需求时，nn.functional.xxx是更佳的选择，因为nn.functional.xxx更加的灵活(更加接近底层），你可以在其基础上定义出自己想要的功能。
7.个人偏向于在能使用nn.Xxx情况下尽量使用，不行再换nn.functional.xxx ，感觉这样更能显示出网络的层次关系，也更加的纯粹（所有layer和model本身都是Module，一种和谐统一的感觉）。

三、torch.autograd

1.torch.autograd提供了类和函数用来对任意标量函数进行求导。要想使用自动求导，只需要对已有的代码进行微小的改变。只需要将所有的tensor包含进Variable对象中即可。
2.Variable对象几乎和 Tensor 一致 (除了一些in-place方法，这些in-place方法会修改 required_grad=True的 input 的值)。多数情况下，将Tensor替换为Variable，代码一样会正常的工作。

（一）class torch.autograd.Variable

1.class torch.autograd.Variable。
- 功能是：包装一个Tensor,并记录用在它身上的operations。
- Variable是Tensor对象的一个thin wrapper（SS简单的包裹？），它同时保存着Variable的梯度和创建这个Variable的Function的引用。这个引用可以用来追溯创建这个Variable的整条链。如果Variable是被用户所创建的，那么它的creator是None，我们称这种对象为 leaf Variables。
- Variable对象内包含的变量：
  - data – 包含的Tensor
  - grad – 保存着Variable的梯度。这个属性是懒惰分配的，且不能被重新分配。
  - requires_grad – 布尔值，指示这个Variable是否是被一个包含Variable的子图创建的。
  - volatile – 布尔值，指示这个Variable是否被用于推断模式(即，不保存历史信息)。
  - creator – 创建这个Variable的Function，对于leaf variable，这个属性为None。只读属性。
- 属性
  - data (any tensor class) – 被包含的Tensor
  - requires_grad (bool) – requires_grad标记. 只能通过keyword传入.
  - volatile (bool) – volatile标记. 只能通过keyword传入.
2.backward(gradient=None, retain_variables=False)，是一个使用在variable上的方法。
3.detach()
4.detach_()
5.register_hook(hook)
6.reinforce(reward)，在reinforcement learning中用到，用于强化学习的。

（二）class torch.autograd.Function

1.class torch.autograd.Function
- 功能：记录operation的历史，定义微分公式。
- 具体执行时的流程：每个执行在Varaibles上的operation都会创建一个Function对象，这个Function对象执行计算工作，同时记录下来。这个历史以有向无环图的形式保存下来，有向图的节点为functions，有向图的边代表数据依赖关系(input<-output)。之后，当backward被调用的时候，计算图以拓扑顺序处理，通过调用每个Function对象的backward()，同时将返回的梯度传递给下一个Function。
2.backward(* grad_output)，定义了operation的微分公式。
3.forward(* input)，执行operation。

四、torch.optim

1.torch.optim是一个实现了各种优化算法的库。支持大部分常用的方法，并且这些方法的接口具备足够的通用性，使得未来能够集成更加复杂的方法。
2.为了使用torch.optim，需要构建一个optimizer对象。这个对象能够保持当前参数状态并基于计算得到的梯度进行参数更新。
3.为了构建一个Optimizer，你需要给它一个包含了需要优化的参数（必须都是Variable对象）的iterable。然后，你可以设置optimizer的参数选项，比如学习率，权重衰减，等等。

optimizer = torch.optim.SGD(model.parameters(), lr = 0.01, momentum=0.9)
optimizer = torch.optim.Adam([var1, var2], lr = 0.0001)

5.使用：所有的optimizer都实现了step()方法，一旦梯度被如backward()之类的函数计算好后，我们就可以调用这个函数。

for input, target in dataset:
    optimizer.zero_grad()
    output = model(input)
    loss = loss_fn(output, target)
    loss.backward()
    optimizer.step()

（一）class torch.optim.Optimizer(params, defaults)

1.这是所有optimizers的父类（比如torch.optim.SGD、torch.optim.Adam就是该父类的两个子类），下面列举一些这个父类定义一些的方法。
2.load_state_dict(state_dict)加载optimizer状态
3.state_dict() 以dict返回optimizer的状态。
4.step(closure)
5.zero_grad()

（二）class torch.optim.Adadelta(params, lr=1.0, rho=0.9, eps=1e-06, weight_decay=0)

1.class torch.optim.Adadelta(params, lr=1.0, rho=0.9, eps=1e-06, weight_decay=0)Adadelta算法。
- params (iterable) – 待优化参数的iterable或者是定义了参数组的dict
- rho (float, 可选) – 用于计算平方梯度的运行平均值的系数（默认：0.9）
- eps (float, 可选) – 为了增加数值计算的稳定性而加到分母里的项（默认：1e-6）
- lr (float, 可选) – 在delta被应用到参数更新之前对它缩放的系数（默认：1.0）
- weight_decay (float, 可选) – 权重衰减（L2惩罚）（默认: 0）

（三）class torch.optim.Adagrad(params, lr=0.01, lr_decay=0, weight_decay=0)

1.class torch.optim.Adagrad(params, lr=0.01, lr_decay=0, weight_decay=0)
- params (iterable) – 待优化参数的iterable或者是定义了参数组的dict
- lr (float, 可选) – 学习率（默认: 1e-2）
- lr_decay (float, 可选) – 学习率衰减（默认: 0）
- weight_decay (float, 可选) – 权重衰减（L2惩罚）（默认: 0）

（四）class torch.optim.Adam(params, lr=0.001, betas=(0.9, 0.999), eps=1e-08, weight_decay=0)

1.class torch.optim.Adam(params, lr=0.001, betas=(0.9, 0.999), eps=1e-08, weight_decay=0)实现Adam算法。
- params (iterable) – 待优化参数的iterable或者是定义了参数组的dict
- lr (float, 可选) – 学习率（默认：1e-3）
- betas (Tuple[float, float], 可选) – 用于计算梯度以及梯度平方的运行平均值的系数（默认：0.9，0.999）
- eps (float, 可选) – 为了增加数值计算的稳定性而加到分母里的项（默认：1e-8）
- weight_decay (float, 可选) – 权重衰减（L2惩罚）（默认: 0）

（五）class torch.optim.Adamax(params, lr=0.002, betas=(0.9, 0.999), eps=1e-08, weight_decay=0)Adam的一种基于无穷范数的变种

（六）class torch.optim.ASGD(params, lr=0.01, lambd=0.0001, alpha=0.75, t0=1000000.0, weight_decay=0)

1.class torch.optim.ASGD(params, lr=0.01, lambd=0.0001, alpha=0.75, t0=1000000.0, weight_decay=0)
- params (iterable) – 待优化参数的iterable或者是定义了参数组的dict
- lr (float, 可选) – 学习率（默认：1e-2）
- lambd (float, 可选) – 衰减项（默认：1e-4）
- alpha (float, 可选) – eta更新的指数（默认：0.75）
- t0 (float, 可选) – 指明在哪一次开始平均化（默认：1e6）
- weight_decay (float, 可选) – 权重衰减（L2惩罚）（默认: 0）
2.Asynchronous Stochastic Gradient Descent (ASGD)异步的随机梯度下降在深度学习模型的训练中经常被用到,但是会存在delayed gradients的问题.

(七）class torch.optim.LBFGS(params, lr=1, max_iter=20, max_eval=None, tolerance_grad=1e-05, tolerance_change=1e-09, history_size=100, line_search_fn=None)

1.class torch.optim.LBFGS(params, lr=1, max_iter=20, max_eval=None, tolerance_grad=1e-05, tolerance_change=1e-09, history_size=100, line_search_fn=None)无法单独设置参数

（八）class torch.optim.RMSprop(params, lr=0.01, alpha=0.99, eps=1e-08, weight_decay=0, momentum=0, centered=False)

1.class torch.optim.RMSprop(params, lr=0.01, alpha=0.99, eps=1e-08, weight_decay=0, momentum=0, centered=False)实现RMSprop算法，既AdaGrad算法的改进，是像AdaGrad算法那样暴力直接的累加平方梯度，而是加了一个衰减系数来控制历史信息的获取多少。
- params (iterable) – 待优化参数的iterable或者是定义了参数组的dict
- lr (float, 可选) – 学习率（默认：1e-2）
- momentum (float, 可选) – 动量因子（默认：0）
- alpha (float, 可选) – SS衰减系数（默认：0.99）
- eps (float, 可选) – 为了增加数值计算的稳定性而加到分母里的项（默认：1e-8）
- centered (bool, 可选) – 如果为True，计算中心化的RMSProp，并且用它的方差预测值对梯度进行归一化
- weight_decay (float, 可选) – 权重衰减（L2惩罚）（默认: 0）

（九）class torch.optim.Rprop(params, lr=0.01, etas=(0.5, 1.2), step_sizes=(1e-06, 50))[source]

1.class torch.optim.Rprop(params, lr=0.01, etas=(0.5, 1.2), step_sizes=(1e-06, 50))[source]弹性反向传播算法。

（十）class torch.optim.SGD(params, lr=, momentum=0, dampening=0, weight_decay=0, nesterov=False)

1.class torch.optim.SGD(params, lr=, momentum=0, dampening=0, weight_decay=0, nesterov=False)随机梯度下降算法
- params (iterable) – 待优化参数的iterable或者是定义了参数组的dict
- lr (float) – 学习率
- momentum (float, 可选) – 动量因子（默认：0）
- weight_decay (float, 可选) – 权重衰减（L2惩罚）（默认：0）
- dampening (float, 可选) – 动量的抑制因子（默认：0）
- nesterov (bool, 可选) – 使用Nesterov动量（默认：False）
2.只在mini-batch上计算就回传梯度，而不用走完一个epoch再走一步，因此速度快，还具有自动脱离鞍点等等好处。

五、torch.nn.init

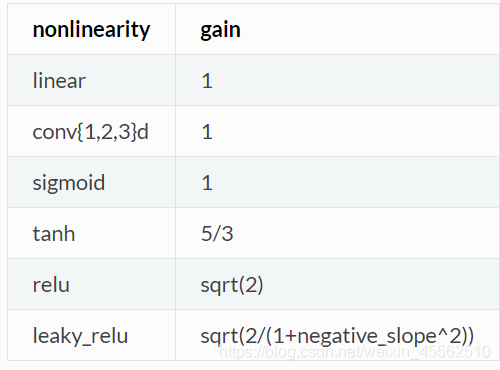
（一）torch.nn.init.calculate_gain(nonlinearity,param=None)

1.对于给定的非线性函数，返回推荐的增益值。SS我感觉你不嫌烦甚至可以直接背下来。

（二）pytorch使用时的权值初始化问题相关

来源：https://zhuanlan.zhihu.com/p/210137182

1.再不使用激活函数的情况下，可证明二不证明，每经过一个网络层，方差就会扩大 n 倍，标准差就会扩大 sqr(n) 倍。在初始化时，为保证正向不积累n倍发生爆炸，反向不缩小为1\n造成梯度消失，使用以下方式初始化（不妨使用normal方式初始化），nn.init.normal_(m.weight.data, std=np.sqrt(1/self.neural_num))
修改后一97层网络效果如下。

layer:0, std:0.9974957704544067
layer:1, std:1.0024365186691284
layer:2, std:1.002745509147644
.
.
.
layer:94, std:1.031973123550415
layer:95, std:1.0413124561309814
layer:96, std:1.0817031860351562

修改之后，没有出现梯度消失或者梯度爆炸的情况，每层神经元输出的方差均在 1 左右。通过恰当的权值初始化，可以保持权值在更新过程中维持在一定范围之内，不过过大，也不会过小。
2.在使用非线性变换时，每一层的输出方差还是会越来越小，会导致梯度消失。因此出现了 Xavier 初始化方法与 Kaiming 初始化方法。
3.Xavier 初始化方法

借用pytorch提供的简单写法：
tanh_gain = nn.init.calculate_gain('tanh')
nn.init.xavier_uniform_(m.weight.data, gain=tanh_gain)

但这一段内部实际上进行的工作是：
a = np.sqrt(6 / (self.neural_num + self.neural_num))
# 把 a 变换到 tanh，计算增益
tanh_gain = nn.init.calculate_gain('tanh')
a *= tanh_gain

nn.init.uniform_(m.weight.data, -a, a)

4.这里就用到了上面提到的calculate_gain函数。
5.Kaiming 方法：这种方法就抛弃了sigmoid和tanh激活函数，开始使用ReLU方法。

手动方法：
nn.init.normal_(m.weight.data, std=np.sqrt(2 / self.neural_num))
借用pytorch初始化
nn.init.kaiming_normal_(m.weight.data)

（三）介绍各类初始化方法

1.Reference:https://www.aiuai.cn/aifarm613.html

import torch
import torch.nn as nn

w = torch.empty(2, 3)

# 1. 均匀分布 - u(a, b)
# torch.nn.init.uniform_(tensor, a=0, b=1)
nn.init.uniform_(w)
# tensor([[ 0.0578,  0.3402,  0.5034],
#         [ 0.7865,  0.7280,  0.6269]])

# 2. 正态分布 - N(mean, std)
# torch.nn.init.normal_(tensor, mean=0, std=1)
nn.init.normal_(w)
# tensor([[ 0.3326,  0.0171, -0.6745],
#        [ 0.1669,  0.1747,  0.0472]])

# 3. 常数 - 固定值 val
# torch.nn.init.constant_(tensor, val)
nn.init.constant_(w, 0.3)
# tensor([[ 0.3000,  0.3000,  0.3000],
#         [ 0.3000,  0.3000,  0.3000]])

#4. 对角线为1， 其它为0
# torch.nn.init.eye_(tensor)
nn.init.eye_(w)
# tensor([[ 1.,  0.,  0.],
#         [ 0.,  1.,  0.]])

# 5. Dirac delta 函数初始化，仅适用于 {3, 4, 5}-维的 torch.Tensor
# torch.nn.init.dirac_(tensor)
w1 = torch.empty(3, 16, 5, 5)
nn.init.dirac_(w1)

# 6. xavier_uniform 初始化
# torch.nn.init.xavier_uniform_(tensor, gain=1)
# From - Understanding the difficulty of training deep feedforward neural networks - Bengio 2010
nn.init.xavier_uniform_(w, gain=nn.init.calculate_gain('relu'))
# tensor([[ 1.3374,  0.7932, -0.0891],
#         [-1.3363, -0.0206, -0.9346]])

# 7. xavier_normal 初始化
# torch.nn.init.xavier_normal_(tensor, gain=1)
nn.init.xavier_normal_(w)
# tensor([[-0.1777,  0.6740,  0.1139],
#         [ 0.3018, -0.2443,  0.6824]])

# 8. kaiming_uniform 初始化
# From - Delving deep into rectifiers: Surpassing human-level performance on ImageNet classification - He Kaiming 2015
# torch.nn.init.kaiming_uniform_(tensor, a=0, mode='fan_in', nonlinearity='leaky_relu')
nn.init.kaiming_uniform_(w, mode='fan_in', nonlinearity='relu')
# tensor([[ 0.6426, -0.9582, -1.1783],
#         [-0.0515, -0.4975,  1.3237]])

# 9. kaiming_normal 初始化
# torch.nn.init.kaiming_normal_(tensor, a=0, mode='fan_in', nonlinearity='leaky_relu')
nn.init.kaiming_normal_(w, mode='fan_out', nonlinearity='relu')
# tensor([[ 0.2530, -0.4382,  1.5995],
#         [ 0.0544,  1.6392, -2.0752]])

# 10. 正交矩阵 - (semi)orthogonal matrix
# From - Exact solutions to the nonlinear dynamics of learning in deep linear neural networks - Saxe 2013
# torch.nn.init.orthogonal_(tensor, gain=1)
nn.init.orthogonal_(w)
# tensor([[ 0.5786, -0.5642, -0.5890],
#         [-0.7517, -0.0886, -0.6536]])

# 11. 稀疏矩阵 - sparse matrix 
# 非零元素采用正态分布 N(0, 0.01) 初始化.
# From - Deep learning via Hessian-free optimization - Martens 2010
# torch.nn.init.sparse_(tensor, sparsity, std=0.01)
nn.init.sparse_(w, sparsity=0.1)
# tensor(1.00000e-03 *
#        [[-0.3382,  1.9501, -1.7761],

六、torch.multiprocessing用于共享

七、遗产包 - torch.legacy

八、torch.cuda–来自矿场时代的怨念，GPU暂时用不上

九、torch.utils.ffi看不出来有啥用，先放着

十、torch.utils.data

（一）class torch.utils.data.Dataset

1.表示Dataset的抽象类。所有其他数据集都应该进行子类化。
2.编写者或者大神们去关心，我们就不管了。

（二）class torch.utils.data.TensorDataset(data_tensor, target_tensor)

1.将一个数据张量和目标（SS标签？）张量依据索引联系在一起，构成一个可以被pytorch使用的数据集。

（三）class torch.utils.data.DataLoader(dataset, batch_size=1, shuffle=False, sampler=None, num_workers=0, collate_fn=, pin_memory=False, drop_last=False)

1.功能简述：数据加载器。组合数据集和采样器，并在数据集上提供单进程或多进程迭代器。
2.参数：
- dataset (Dataset) – 加载数据的数据集。
- batch_size (int, optional) – 每个batch加载多少个样本(默认: 1)。
- shuffle (bool, optional) – 设置为True时会在每个epoch重新打乱数据(默认: False).
- sampler (Sampler, optional) – 定义从数据集中提取样本的策略。如果指定，则忽略shuffle参数。
- num_workers (int, optional) – 用多少个子进程加载数据。0表示数据将在主进程中加载(默认: 0)
- collate_fn (callable, optional) –
- pin_memory (bool, optional) –
- drop_last (bool, optional) – 如果数据集大小不能被batch size整除，则设置为True后可删除最后一个不完整的batch。如果设为False并且数据集的大小不能被batch size整除，则最后一个batch将更小。(默认: False)
3.通常使用方法：先设计一个dataset类，实例化之，然后创建dataloader对象。这个对象很想嵌入式SQL语言中使用的游标，可以按照一定的批次访问内部的（数据，标签）。

class DealDataset(Dataset):
    """
        下载数据、初始化数据，都可以在这里完成
    """
    def __init__(self):
        xy = np.loadtxt('../dataSet/diabetes.csv.gz', delimiter=',', dtype=np.float32) # 使用numpy读取数据
        self.x_data = torch.from_numpy(xy[:, 0:-1])
        self.y_data = torch.from_numpy(xy[:, [-1]])
        self.len = xy.shape[0]
    
    def __getitem__(self, index):
        return self.x_data[index], self.y_data[index]

    def __len__(self):
        return self.len

# 实例化这个类，然后我们就得到了Dataset类型的数据，记下来就将这个类传给DataLoader，就可以了。    
dealDataset = DealDataset()

train_loader2 = DataLoader(dataset=dealDataset,
                          batch_size=32,
                          shuffle=True)


for epoch in range(2):
    for i, data in enumerate(train_loader2):
        # 将数据从 train_loader 中读出来,一次读取的样本数是32个
        inputs, labels = data

        # 将这些数据转换成Variable类型
        inputs, labels = Variable(inputs), Variable(labels)

        # 接下来就是跑模型的环节了，我们这里使用print来代替
        print("epoch：", epoch, "的第" , i, "个inputs", inputs.data.size(), "labels", labels.data.size())
————————————————
版权声明：本文为CSDN博主「嘿芝麻」的原创文章，遵循CC 4.0 BY-SA版权协议，转载请附上原文出处链接及本声明。
原文链接：https://blog.csdn.net/zw__chen/article/details/82806900

（三）class torch.utils.data.sampler.Sampler(data_source)

1.所有采样器的基础类。

（四）class torch.utils.data.sampler.SequentialSampler(data_source)

1.样本元素顺序排列，始终以相同的顺序。