【二叉树初阶】前中后序遍历+层序遍历+基础习题

文章目录

🌌前言
🌌前序遍历
🌌中序遍历
🌌后序遍历
🌌前中后序遍历总结
🌌层序遍历
🍂二叉树相关计算一网打尽
🌏二叉树基础练习
🌏基础选择题
🌏二叉树遍历源码

🌌前言

本篇文章将用大白话以及图解讲解二叉树初阶的遍历和相关习题，初学二叉树的小白一看就会。
普通二叉树的增删查改是没有价值的，用它存数据太麻烦，不如用顺序表、链表、至多是完全二叉树存储，所以我们只关注遍历过程，因为学习二叉树最简单的方式就是遍历，也为后面学习搜索二叉树、AVL树、红黑树等打基础

二叉树的遍历分为：前序、中后、后序和层序遍历，这里前中后序遍历用递归实现，层序遍历用非递归实现

🌌前序遍历

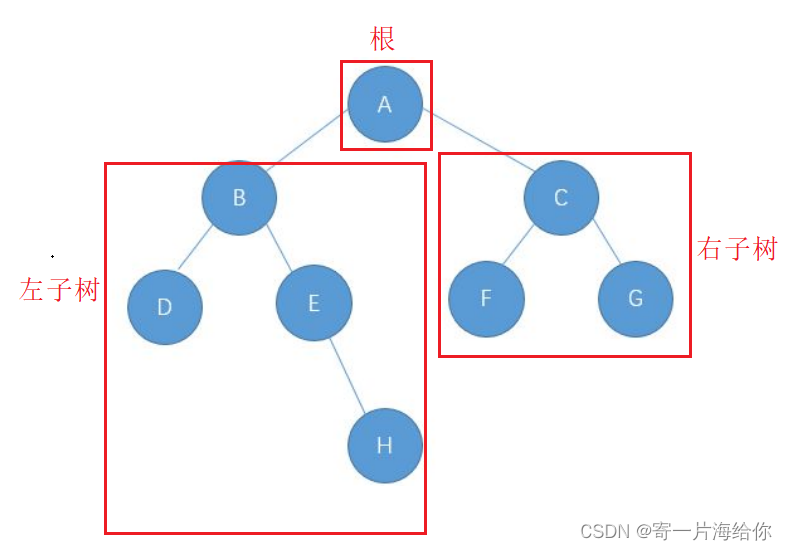
在学习二叉树的遍历之前，在简单提一下二叉树的概念

空树
非空：由根、左子树、右子树组成

前序遍历((Preorder Traversal 也称先序遍历)：先访问根节点，再访问左子树、右子树。前中后序就是访问根节点的时机不同

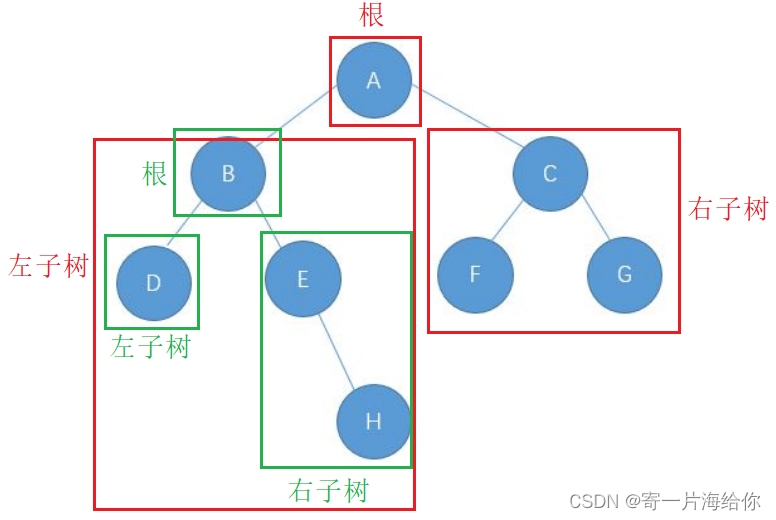
遍历采用分治的思想：将一个大问题，划分为最小规模的子问题。将一颗数不断划分为根、左子树、右子树，直到最后走向空树。这里D还可以当做根节点，左右子树为空
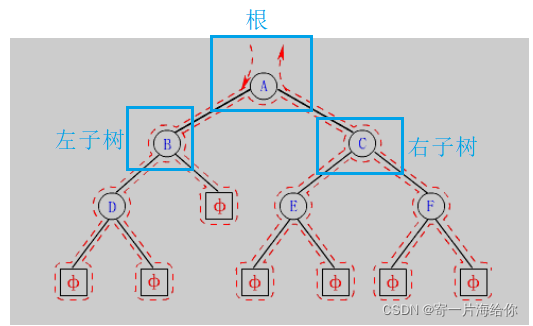
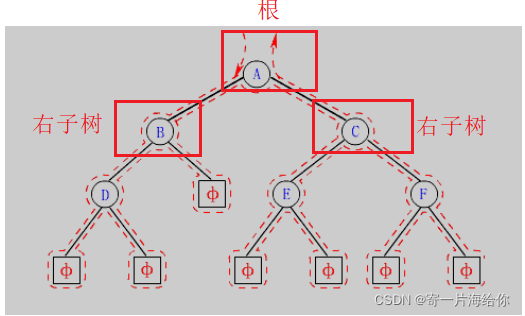
在这里插入图片描述

下图虚线是递归过程，前序：根->左子树->右子树，所以先访问根。
先访问根A，再访问左子树B，B也是根，再访问B的左子树D，D也是根，再访问D的左子树NULL，NULL没有左子树所以再访问D的右子树NULL，往上回归B的左子树访问完了，再访问B的右子树…一直划分一直递归
最后前序遍历顺序为：A->B->D->NULL->NULL->NULL->C->E->NULL->NULL->F->NULL->NULL

暴力建一个和上图同样结构的二叉树

typedef char BTDataType;
typedef struct BinaryTreeNode 
{
	struct BinaryTreeNode* left;
	struct BinaryTreeNode* right;
	BTDataType val;
}BTNode;
//构造节点
BTNode* CreateNode(BTDataType x) 
{
	BTNode* newnode = (BTNode*)malloc(sizeof(BTNode));
	newnode->left = newnode->right = NULL;
	newnode->val = x;
	return newnode;
}
//构造二叉树
BTNode* CreateBTree() 
{
	BTNode* nodeA = CreateNode('A');
	BTNode* nodeB = CreateNode('B');
	BTNode* nodeC = CreateNode('C');
	BTNode* nodeD = CreateNode('D');
	BTNode* nodeE = CreateNode('E');
	BTNode* nodeF = CreateNode('F');
	nodeA->left = nodeB;
	nodeA->right = nodeC;
	nodeB->left = nodeD;
	nodeC->left = nodeE;
	nodeC->right = nodeF;
	return nodeA;
}

根据前序遍历先访问根再访问左子树、右子树。递归实现就不能多想，想到第一步大思路就是代码的实现，比如求100的阶乘，想到100*99!就不要想了，这就是代码的实现。
这里同样如此，前序遍历：先遍历根，在遍历左子树根->left，再遍历右子树根->right，这就是实现的代码
在这里插入图片描述
这里要把NULL也打印出来，空才能体现遍历的精髓，最开始一定要把NULL写出来方便理解

//前序遍历：根->左子树->右子树
void PreOrder(BTNode* root)
 {
 	//当前节点为空时，打印空再返回上一层调用
	if (root == NULL) {
		printf("NULL ");
		return;
	}
	printf("%c ", root->val);//空
	PreOrder(root->left);//左子树
	PreOrder(root->right);//右子树
}
int main()
{
	BTNode* root = CreateBTree();
	printf("前序：");
	PreOrder(root);
}

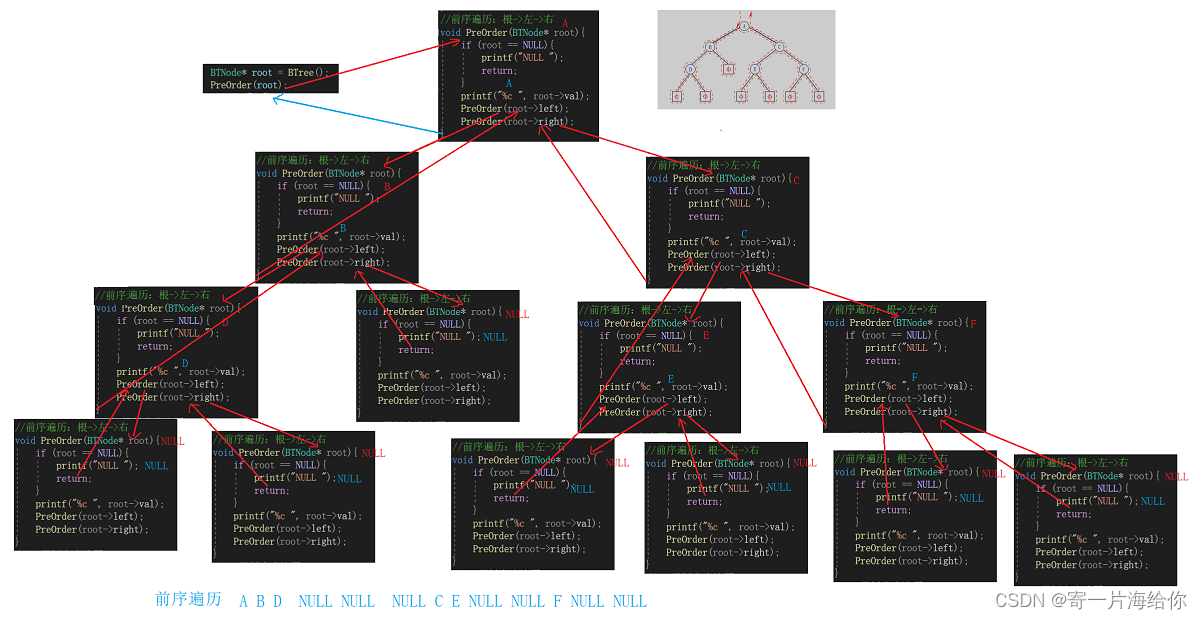
递归展开图，蓝色为打印结果在这里插入图片描述

🌌中序遍历

中序遍历(Inorder Traversal)：左子树->根->右子树（根节点在中间访问），同样是这张图
先访问左子树，也就是B，但不能先访问B，因为B也可当做根节点应该先访问B的左子树D，但不能先访问D，因为D也可当做根节点应该先访问D的左子树NULL，再访问根D，再访问右子树NULL，然后再往回返…按照左子树->根->右子树的顺序访问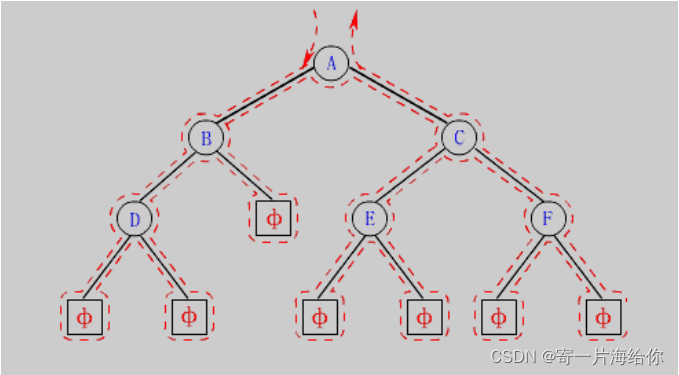在这里插入图片描述可以理解为把A的左子树往左拉成一条直线依次访问，然后访问A，再把A的右子树往左拉成一条直接依次访问
中序遍历：：NULL-> D->NULL-> B->NULL-> A-> NULL-> E-> NULL-> C-> NULL-> F-> NULL

中序遍历实现和前序遍历的类似，只是访问时机不同

// 二叉树中序遍历
void InOrder(BTNode* root)
{
	if (root == NULL)
	{
		printf("NULL ");
		return;
	}
	InOrder(root->left);//左子树
	printf("%c ", root->val);//根
	InOrder(root->right);//右子树
}

🌌后序遍历

后序遍历(Postorder Traversal)：访问顺序左子树->右子树->根（根最后访问）
一直往下找左子树，先访问D的左子树NULL，再访问D的右子树NULL，再访问根D，然后往上回归B的左子树访问完了，访问B的右子树NULL，再访问根B，再往上回归…
在这里插入图片描述后序：NULL-> NULL-> D-> NULL-> B-> NULL -> NULL-> E-> NULL-> NULL-> F-> C-> A

// 二叉树后序遍历
void PostOrder(BTNode* root)
{
	if (root == NULL)
	{
		printf("NULL ");
		return;
	}
	PostOrder(root->left);//左子树
	PostOrder(root->right);//右子树
	printf("%c ", root->val);//根
}

🌌前中后序遍历总结

前中后序遍历就是访问根节点的时机不同，先访问根就是前序遍历，在中间访问根就是中序遍历，最后访问根就是后序遍历。

前序遍历第一个节点就是整个二叉树的根节点
中序遍历第一个节点就是整个二叉树最左边的节点
后序遍历最后一个节点就是整个二叉树的根节点

🌌层序遍历

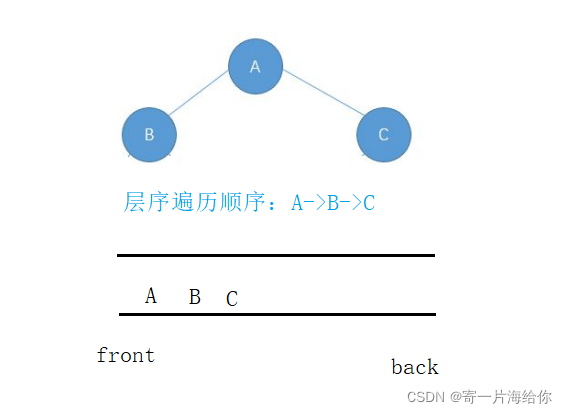
层序遍历就是自顶向下，从左到右访问。我们可以借助队列queue完成遍历，先进队列的先出队列，
先举一个简单的例子：相办法让A B C依次进队列，可以先让A进队列，然后让A出队列再把A的左右孩子B、C进队列。也就是根先进队列，然后front队头出队列，再把front队头的左右孩子入进队列，这样通过迭代就可以实现层序遍历
在这里插入图片描述
由于C语言没有标准模板库，所以需要自己实现一个队列，这里直接调用我已经实现好的，在源码有具体实现。ps：层序遍历没有打印NULL

// 层序遍历
void LevelOrder(BTNode* root)
{	
	if (root == NULL)
		return;
	Queue q;
	//queue初始化
	QueueInit(&q);
	//先将根push进queue
	QueuePush(&q, root);
	while (!QueueEmpty(&q))
	{
		BTNode* front = QueueFront(&q);
		printf("%c ", front->val);
		//父亲出队列
		QueuePop(&q);//pop掉的只是指针的值，所以不会释放指针所指空间
		//孩子不为NULL时进队列
		if (front->left)
			QueuePush(&q, front->left);
		if (front->right)
			QueuePush(&q, front->right);
	}
	QueueDestroy(&q);
}

🍂二叉树相关计算一网打尽

🪐节点个数

要计算节点个数，就把B当做根的左子树，C当做根的右子树，左子树+右子树+1就是节点个数，也就是节点个数=根->left+根->right+1，想到这里就不要想了，直接实现代码
在这里插入图片描述

//计算节点个数
int BTreeSize(BTNode* root)
{
	if (root == NULL)
		return 0;
	return BTreeSize(root->left) + BTreeSize(root->right) + 1;
}

🪐叶子节点个数

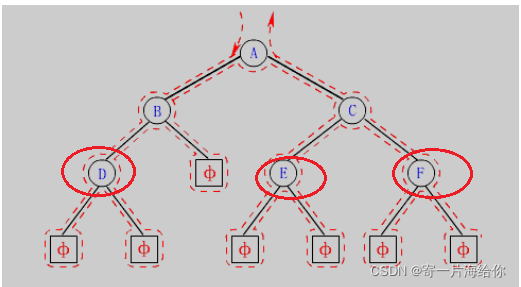
叶子节点就是没有孩子的节点，D、E、F就是叶子节点
在这里插入图片描述
所以只需要节点->left和节点->right的为NULL就是叶子节点，然后继续遍历计算

//计算叶子节点个数
int BTreeLeafSize(BTNode* root)
{
	if (root == NULL)
		return 0;
	if (root->left == NULL && root->right == NULL)
		return 1;
	return BTreeLeafSize(root->left) + BTreeLeafSize(root->right);//继续遍历
}

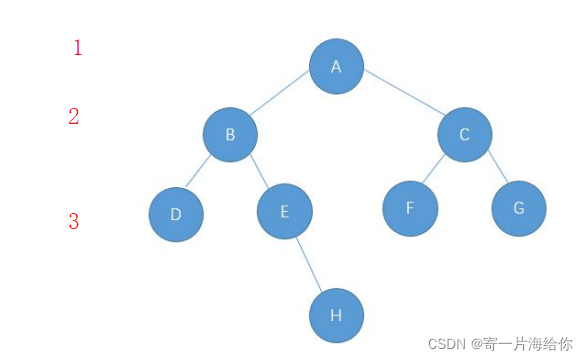
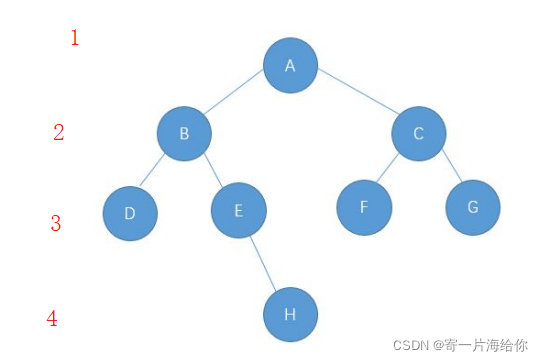
🪐第k层节点个数

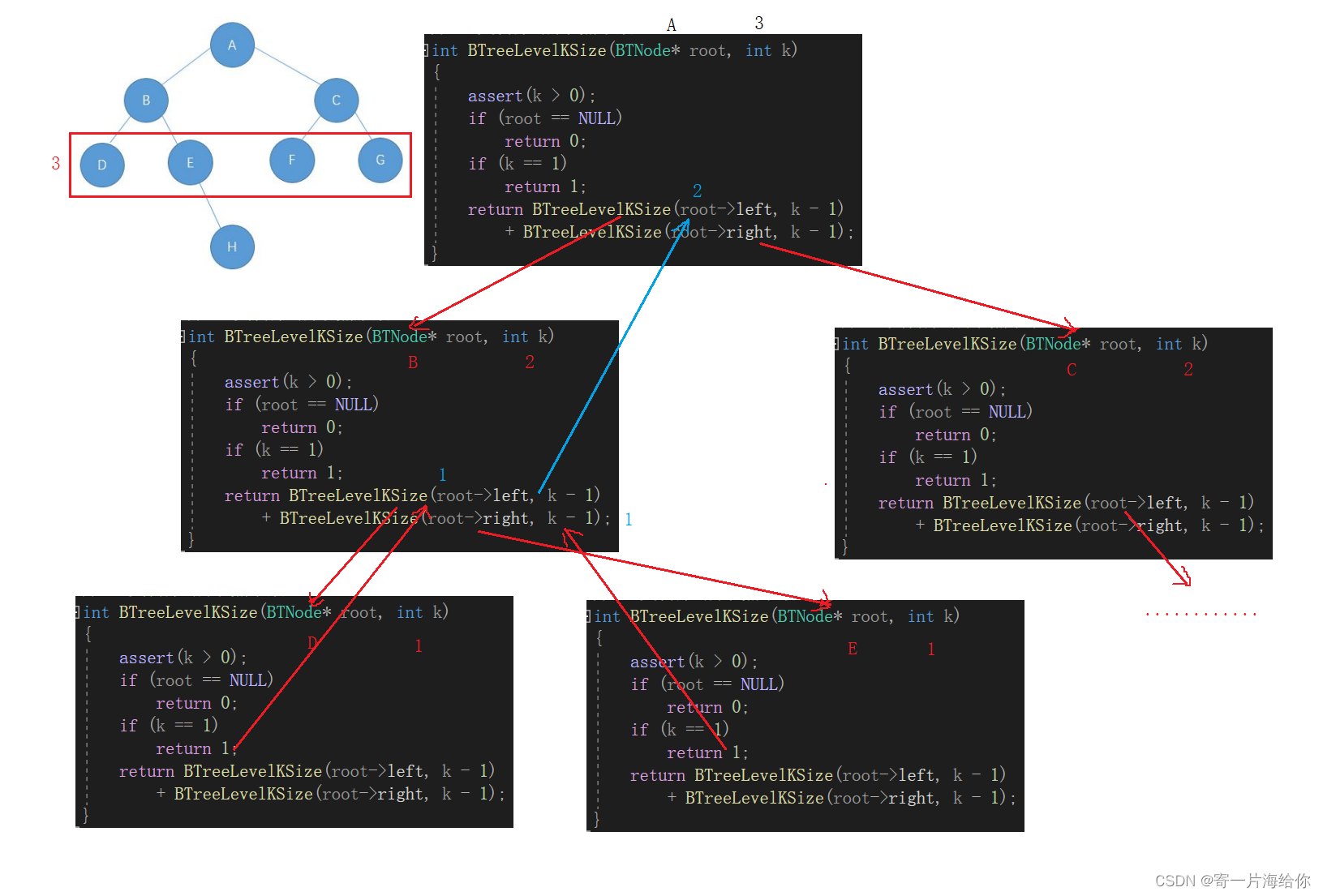
以空数为0层。比如要计算第3层节点个数就是计算左子树第二层+右子树第二层节点个数，root根的第三层节点=roo->left的第二层节点+roo->right的第二层节点… 在这里插入图片描述

// 二叉树第k层节点个数
int BTreeLevelKSize(BTNode* root, int k)
{
	assert(k > 0);
	if (root == NULL)
		return 0;
	if (k == 1)
		return 1;
	return BTreeLevelKSize(root->left, k - 1) + BTreeLevelKSize(root->right, k - 1);
}

递归展开图，这里只画了左子树的
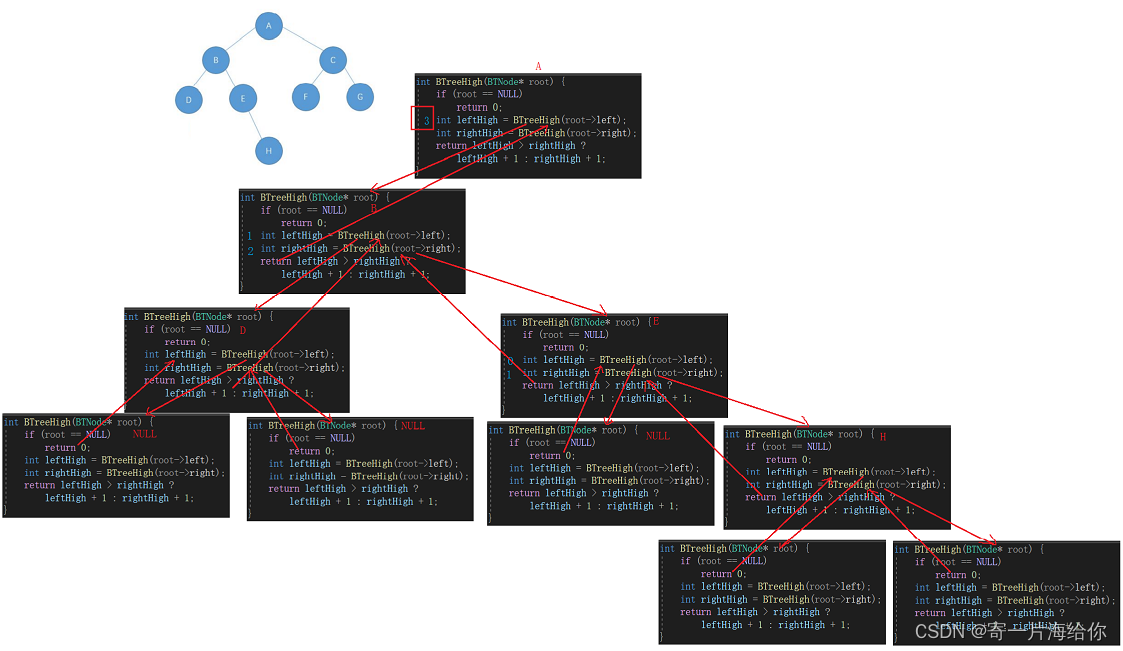
在这里插入图片描述

🪐二叉树高度

数的高度也叫深度，空数高度取0。高度=max(根的左子树高度,右子树高度取)+1
在这里插入图片描述

// 二叉树高度--后序思想
int BTreeHigh(BTNode* root) {
	if (root == NULL)
		return 0;
	int leftHigh = BTreeHigh(root->left);//左子树高度
	int rightHigh = BTreeHigh(root->right);//右子树高度
	return leftHigh > rightHigh ? leftHigh + 1 : rightHigh + 1;
}

递归展开图，这里只计算了A的左子树高度3，计算完右子树后和左子树取较大值+1就是数的高度
在这里插入图片描述

🪐查找值为x的节点

惯性思维，要从数中查找节点肯定是先从根开始，再找左子树，然后再找右子树，直到找到

// 二叉树查找值为x的节点--前序思想
BTNode* BTreeFind(BTNode* root, BTDataType x) {
	if (root == NULL)
		return NULL;
	if (root->val == x)
		return root;
	BTNode* left = BTreeFind(root->left, x);
	if (left)
		return left;
	BTNode* right = BTreeFind(root->right, x);
	if (right)
		return right;
	return NULL;//最后还未找到就返回NULL
}

🪐二叉树销毁

二叉树的递归创建在下面例题有代码实现
从下往上free，先free左右子树，再free根

// 二叉树销毁--后序思想
void BinaryTreeDestory(BTNode* root)
{
	if (root == NULL)
		return;
	BinaryTreeDestory(root->left);
	BinaryTreeDestory(root->right);
	free(root);
}

🪐判断二叉树是否是完全二叉树

完全二叉树有一个特性：前N-1层都是满的，最后一层不满，但从左向右是连续的。当然满二叉树也是特殊的完全二叉树
在这里插入图片描述那么我们只需要按照层序遍历的思想，父亲出queue孩子进queue，节点为NULL也进队列，那么当队头NULL时，当前队列的所有元素都要为空才满足完全二叉树的特性

// 判断二叉树是否是完全二叉树--层序遍历思想
bool BTreeComplete(BTNode* root)
{
	Queue q;
	QueueInit(&q);
	QueuePush(&q, root);
	while (!QueueEmpty(&q))
	{	
		BTNode* front = QueueFront(&q);
		//遇到空时，需要队列的节点都为空，才是完全二叉树
		if (front == NULL)
		{
			//检查队列节点是否都为NULL
			while (!QueueEmpty(&q))
			{	
				front = QueueFront(&q);
				if (front != NULL)
				{
					QueueDestroy(&q);
					return false;
				}
				QueuePop(&q);
			}
			break;
		}
		//父亲出队列
		QueuePop(&q);//pop掉的只是指针的值，而不是所指空间
		//孩子进队列
		QueuePush(&q, front->left);
		QueuePush(&q, front->right);
	}
	QueueDestroy(&q);
	return true;
}

🌏二叉树基础练习

LeetCode965：单值二叉树
在这里插入图片描述题目给定

struct TreeNode {
     int val;
     struct TreeNode *left;
     struct TreeNode *right;
 };
 bool isUnivalTree(struct TreeNode* root){}

思路：只需要比较所有节点个数是否相等，那就先把根和左孩子右孩子比较，然后就开始写代码不能再想了

bool isUnivalTree(struct TreeNode* root){
    if  (root == NULL)
        return true;
     //left不为空时
    if (root->left && root->val != root->left->val)
        return false;
      //right不为空时
    if (root->right && root->val != root->right->val)
        return false;
    return isUnivalTree(root->left) && isUnivalTree(root->right);
}

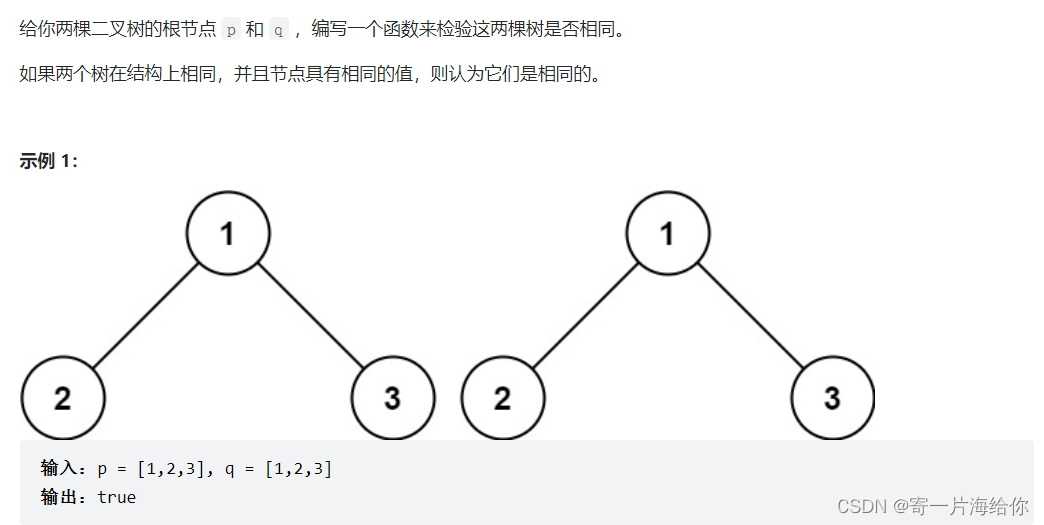
LeetCode100 ：相同的数
在这里插入图片描述题目给定

 struct TreeNode {
      int val;
      struct TreeNode *left;
      struct TreeNode *right;
  };
  bool isSameTree(struct TreeNode* p, struct TreeNode* q){}

思路：同样分别遍历两树，依次比较节点的val是否相同，只要有一个不相同就返回false

bool isSameTree(struct TreeNode* p, struct TreeNode* q){
		//两树节点都为空时，返回true给上一层
    if (p == NULL && q == NULL)
        return true;
     //如果只有一个为空表明不相同，返回false给上一层，出现了false那最后就会返回假了
    if (p==NULL || q == NULL)
        return false;
    if (p->val != q->val)
        return false;
    return isSameTree(p->left,q->left)&&isSameTree(p->right,q->right);
}

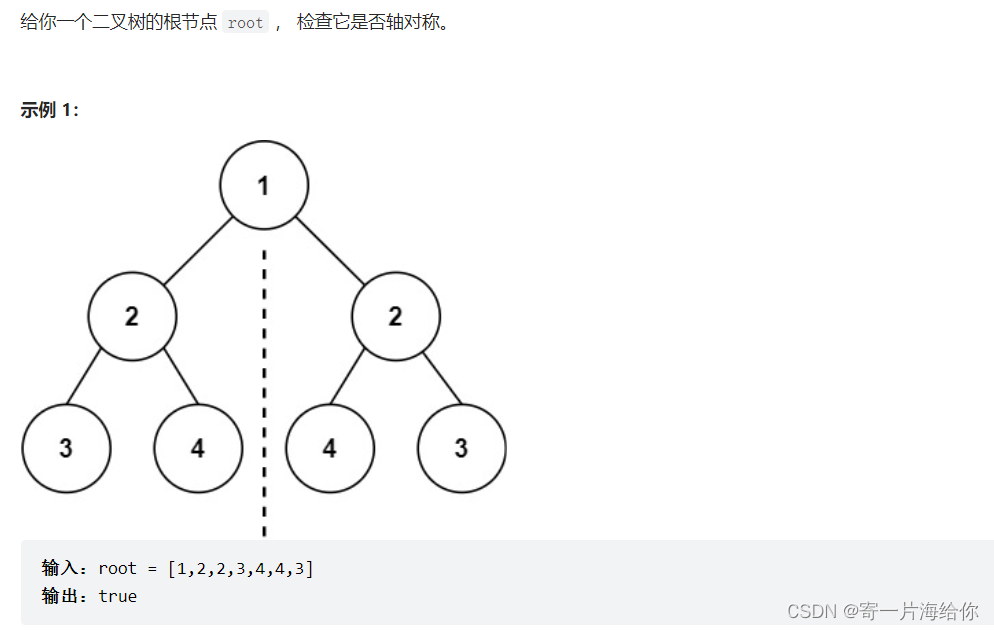
Leet101：对称二叉树
在这里插入图片描述结构

 struct TreeNode {
      int val;
      struct TreeNode *left;
      struct TreeNode *right;
  };

思路：这道题就是求两数是否相同的变形，只不过这里是拿一棵树比较且是left和right比较，root的val为1时是那root->left的val和root->right的val比较，OK想到这里就直接写代码
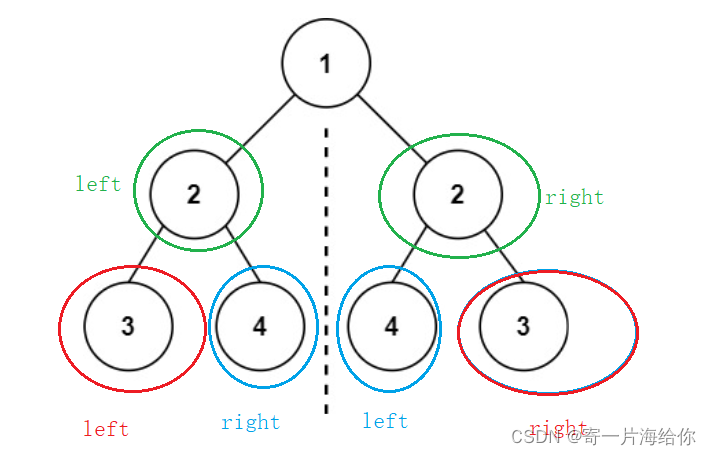
在这里插入图片描述我们可以写一个子函数用来当做比较两树是否相同

bool _isSymmetric(struct TreeNode* root1, struct TreeNode* root2)
{
   if (root1== NULL && root2 == NULL)
       return true;
   if (root1 == NULL || root2 == NULL)
       return false;
   if (root1->val != root2->val)
       return false;
   return _isSymmetric(root1->left, root2->right)&&_isSymmetric(root1->right,root2->left);
}
bool isSymmetric(struct TreeNode* root){
   if (root == NULL)
       return true;
   return _isSymmetric(root->left, root->right);
}

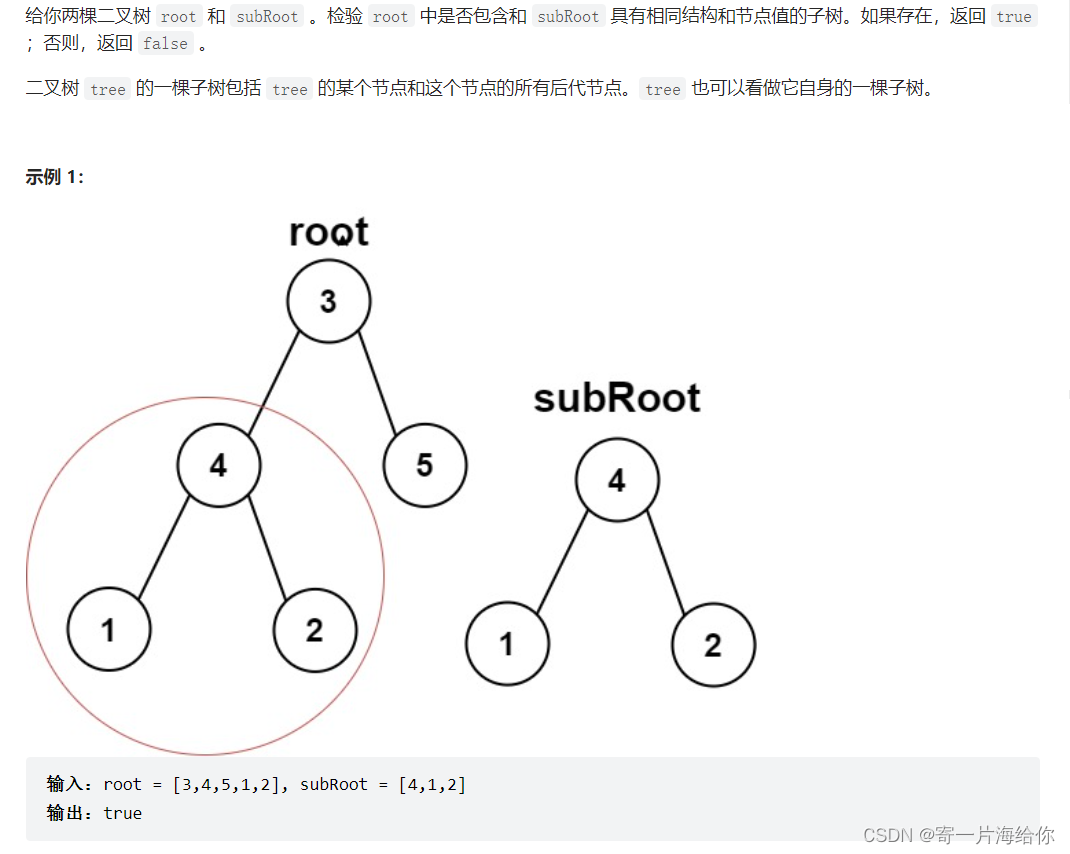
LeetCode572：另一棵树的子树
在这里插入图片描述题目给定

 struct TreeNode {
      int val;
      struct TreeNode *left;
      struct TreeNode *right;
  };
  bool isSubtree(struct TreeNode* root, struct TreeNode* subRoot){}

思路：这道题还是求两颗数是否相同的变形，大思路就是拿root的每一个子树都与subRoot比较两树是否相同，同样写一个子函数执行比较

bool isSameTree(struct TreeNode* p, struct TreeNode* q){
   if (p == NULL && q == NULL)
       return true;
   if (p==NULL || q == NULL)
       return false;
   if (p->val != q->val)
       return false;
   return isSameTree(p->left,q->left)&&isSameTree(p->right,q->right);
}
//用root的每个子树都和subRoot比较
bool isSubtree(struct TreeNode* root, struct TreeNode* subRoot){
   if (root == NULL)
       return false;
   if (isSameTree(root,subRoot))
       return true;
   return isSubtree(root->left,subRoot) || isSubtree(root->right,subRoot);
}

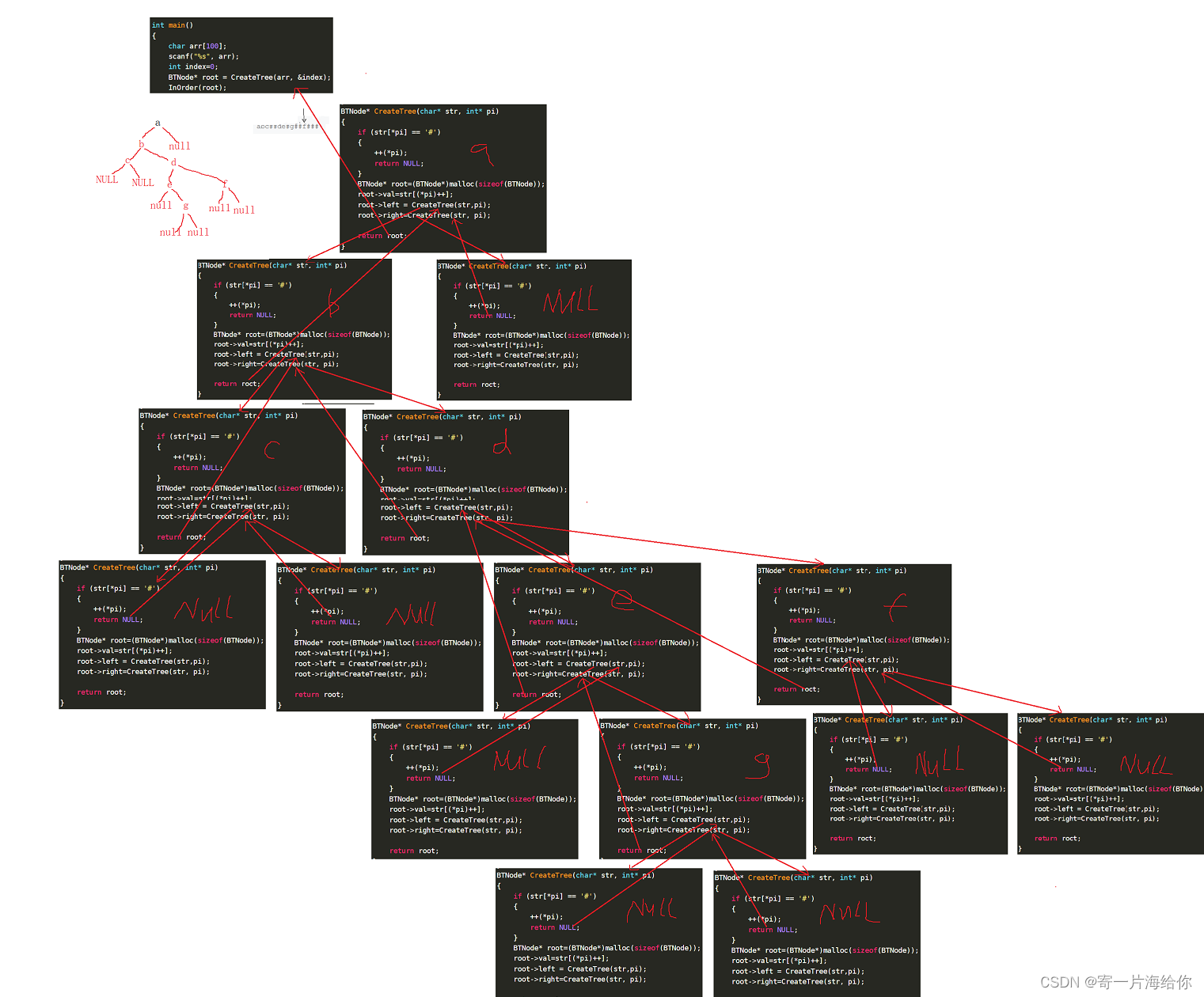
牛客KY11：二叉树遍历
这是一道IO型的题目需要自己写输入输出
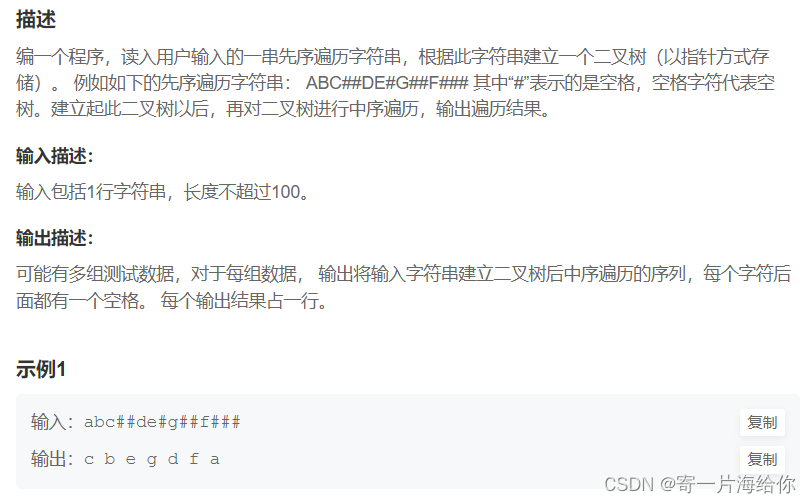
在这里插入图片描述思路：由于输入的是先序遍历的字符串，也就是根->左子树->右子树，我们只需要按照这样的结构复原创建对应的二叉树即可，然后再中序遍历输出结果。所以需要定义CreteTree建树和InOrder函数中序遍历。ps：CreateTree函数会不断往下递推最后回归链接。当递归到最后一个#也就是空时，会返回上一层调用的函数，最后再返回root给main函数

#include <stdio.h>
#include <stdlib.h>

typedef struct BTNode
{
    struct BTNode* left;
    struct BTNode* right;
    char val;
}BTNode;
//建树
BTNode* CreateTree(char* str, int* pi)
{
    if (str[*pi] == '#')
    {    
        ++(*pi);
        return NULL;
    }
    BTNode* root=(BTNode*)malloc(sizeof(BTNode));
    root->val=str[(*pi)++];//根
    root->left = CreateTree(str,pi);//左
    root->right=CreateTree(str, pi);//右
    
    return root;
}
//中序遍历：左->根->右
void InOrder(BTNode* root)
{
    if (root == NULL)
        return;
    InOrder(root->left);
    printf("%c ", root->val);
    InOrder(root->right);
}

int main()
{  
	//题目已经给出字符串长度不超过100,所以直接定义一个100个大小的数组  
    char arr[100];
    scanf("%s", arr);
    int index=0;//index遍历数组
    //这里需要传地址而不能传值，因为传值形参的改变不会影响实参，所以不会及时更新，需要传地址
    BTNode* root = CreateTree(arr, &index);
    InOrder(root);
    
    return 0;
}

递归展开图
在这里插入图片描述

🌏基础选择题

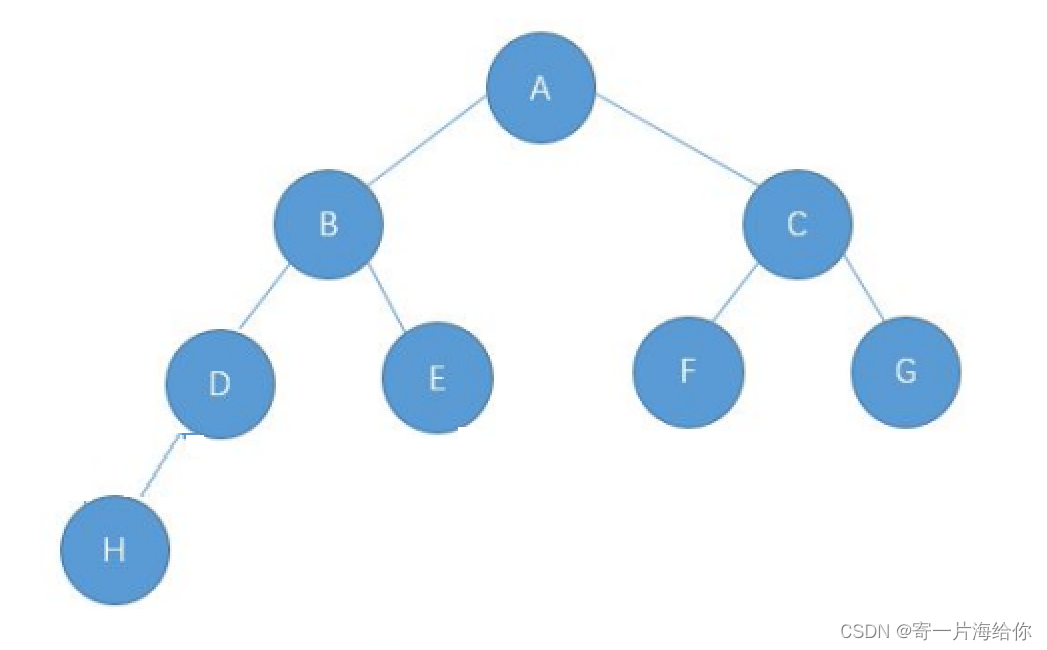
1.某完全二叉树按层次输出（同一层从左到右）的序列为 ABCDEFGH 。该完全二叉树的前序序列为
A ABDHECFG
B ABCDEFGH
C HDBEAFCG
D HDEBFGCA
正确答案：A。
层序遍历顺序为： ABCDEFGH ，根据排出法就可以pass掉BCD了
在这里插入图片描述

2.二叉树的先序遍历和中序遍历如下：先序遍历：EFHIGJK;中序遍历：HFIEJKG.则二叉树根结点为
A E
B F
C G
D H
正确答案：A
根据先序遍历：根->左子树->右子树，所以第一个就是根节点
3.设一课二叉树的中序遍历序列：BADCE，后序遍历序列：BDECA，则二叉树前序遍历序列为____。
A ADBCE
B DECAB
C DEBAC
D ABCDE
正确答案：D
根据后续遍历确定树的根节点A，根据中序遍历确定B为左子树，DCE为右子树，
在这里插入图片描述

4.某二叉树的后序遍历序列与中序遍历序列相同，均为 ABCDEF ，则按层次输出（同一层从左到右）的序列为
A FEDCBA
B CBAFED
C DEFCBA
D ABCDEF
正确答案：A。根据中后序画出二叉树结构图
在这里插入图片描述

🌏二叉树遍历源码

BinaryTree.c

#define _CRT_SECURE_NO_WARNINGS 1
#include "Queue.h"

typedef char BTDataType;
typedef struct BinaryTreeNode 
{
	struct BinaryTreeNode* left;
	struct BinaryTreeNode* right;
	BTDataType val;
}BTNode;
BTNode* CreateNode(BTDataType x) 
{
	BTNode* newnode = (BTNode*)malloc(sizeof(BTNode));
	newnode->left = newnode->right = NULL;
	newnode->val = x;
	return newnode;
}
BTNode* CreateBTree() 
{
	BTNode* nodeA = CreateNode('A');
	BTNode* nodeB = CreateNode('B');
	BTNode* nodeC = CreateNode('C');
	BTNode* nodeD = CreateNode('D');
	BTNode* nodeE = CreateNode('E');
	BTNode* nodeF = CreateNode('F');
	//BTNode* nodeG = CreateNode('G');
	nodeA->left = nodeB;
	nodeA->right = nodeC;
	nodeB->left = nodeD;
	nodeC->left = nodeE;
	nodeC->right = nodeF;
	//nodeB->right = nodeG;
	return nodeA;
}
//前序遍历：根->左子树->右子树
void PreOrder(BTNode* root) {
	if (root == NULL) {
		printf("NULL ");
		return;
	}
	printf("%c ", root->val);
	PreOrder(root->left);
	PreOrder(root->right);
}
// 二叉树中序遍历
void InOrder(BTNode* root)
{
	if (root == NULL)
	{
		printf("NULL ");
		return;
	}
	InOrder(root->left);
	printf("%c ", root->val);
	InOrder(root->right);
}
// 二叉树后序遍历
void PostOrder(BTNode* root)
{
	if (root == NULL)
	{
		printf("NULL ");
		return;
	}
	PostOrder(root->left);
	PostOrder(root->right);
	printf("%c ", root->val);
}
// 层序遍历
void LevelOrder(BTNode* root)
{	
	if (root == NULL)
		return;
	Queue q;
	QueueInit(&q);
	QueuePush(&q, root);
	while (!QueueEmpty(&q))
	{
		BTNode* front = QueueFront(&q);
		printf("%c ", front->val);
		//父亲出队列
		QueuePop(&q);//pop掉的只是指针的值，而不是所指空间
		//孩子进队列
		if (front->left)
			QueuePush(&q, front->left);
		if (front->right)
			QueuePush(&q, front->right);
	}
	QueueDestroy(&q);
}
// 判断二叉树是否是完全二叉树--层序遍历思想
bool BTreeComplete(BTNode* root)
{
	Queue q;
	QueueInit(&q);
	QueuePush(&q, root);
	while (!QueueEmpty(&q))
	{	
		BTNode* front = QueueFront(&q);
		//遇到空时，需要队列的节点都为空，才是完全二叉树
		if (front == NULL)
		{
			while (!QueueEmpty(&q))
			{	
				front = QueueFront(&q);
				if (front != NULL)
				{
					QueueDestroy(&q);
					return false;
				}
				QueuePop(&q);
			}
			break;
		}
		//父亲出队列
		QueuePop(&q);//pop掉的只是指针的值，而不是所指空间
		//孩子进队列
		QueuePush(&q, front->left);
		QueuePush(&q, front->right);
	}
	QueueDestroy(&q);
	return true;
}

//计算节点个数
int BTreeSize(BTNode* root)
{
	if (root == NULL)
		return 0;
	return BTreeSize(root->left) + BTreeSize(root->right) + 1;
}
//计算叶子节点个数
int BTreeLeafSize(BTNode* root)
{
	if (root == NULL)
		return 0;
	if (root->left == NULL && root->right == NULL)
		return 1;
	return BTreeLeafSize(root->left) + BTreeLeafSize(root->right);
}
// 二叉树第k层节点个数
int BTreeLevelKSize(BTNode* root, int k)
{
	assert(k > 0);
	if (root == NULL)
		return 0;
	if (k == 1)
		return 1;
	return BTreeLevelKSize(root->left, k - 1) + BTreeLevelKSize(root->right, k - 1);
}
// 二叉树高度--后序思想
int BTreeHigh(BTNode* root) {
	if (root == NULL)
		return 0;
	int leftHigh = BTreeHigh(root->left);
	int rightHigh = BTreeHigh(root->right);
	return leftHigh > rightHigh ? leftHigh + 1 : rightHigh + 1;
}
// 二叉树查找值为x的节点--前序思想
BTNode* BTreeFind(BTNode* root, BTDataType x) {
	if (root == NULL)
		return NULL;
	if (root->val == x)
		return root;
	BTNode* left = BTreeFind(root->left, x);
	if (left)
		return left;
	BTNode* right = BTreeFind(root->right, x);
	if (right)
		return right;
	return NULL;
}
// 二叉树销毁--后序思想
void BinaryTreeDestory(BTNode* root)
{
	if (root == NULL)
		return;
	BinaryTreeDestory(root->left);
	BinaryTreeDestory(root->right);
	free(root);
}
int main()
{
	BTNode* root = CreateBTree();
	printf("前序：");
	PreOrder(root);
	printf("\n");
	printf("中序：");
	InOrder(root);
	printf("\n");
	printf("后序：");
	PostOrder(root);
	printf("\n");
	printf("层序：");
	LevelOrder(root);
	printf("\n");
	printf("%d\n", BTreeComplete(root));
	printf("BTreeSize=%d\n", BTreeSize(root));
	printf("BTreeLeafSize=%d\n", BTreeLeafSize(root));
	printf("BTreeLevelKSize=%d\n", BTreeLevelKSize(root, 3));
	printf("BTreeHigh=%d\n", BTreeHigh(root));
	BTNode* ret = BTreeFind(root, 'C');
	if (ret != NULL)
		printf("找到了\n");
	else
		printf("没找到\n");

	BinaryTreeDestory(root);
	root = NULL;

	return 0;
}

Queue.c

#define _CRT_SECURE_NO_WARNINGS 1

#include "Queue.h"

void QueueInit(Queue* pq)
{	
	assert(pq);

	pq->head = pq->tail = NULL;
}

void QueuePush(Queue* pq, DataType x)
{
	assert(pq);

	QueueNode* newnode = (QueueNode*)malloc(sizeof(QueueNode));
	newnode->data = x;
	newnode->next = NULL;
	if (pq->head == NULL)
		pq->head = pq->tail = newnode;
	else
	{	
		pq->tail->next = newnode;
		pq->tail = newnode;
	}
}

void QueueDestroy(Queue* pq)
{
	assert(pq);

	QueueNode* cur = pq->head;
	while (cur)
	{
		QueueNode* next = cur->next;
		free(cur);
		cur = next;
	}
}

bool QueueEmpty(Queue* pq)
{
	assert(pq);

	return pq->head == NULL; //队列为空返回true，不为空返回false
}

void QueuePop(Queue* pq)
{
	assert(pq && !QueueEmpty(pq));

	QueueNode* next = pq->head->next;
	free(pq->head);
	pq->head = next;

	if (pq->head == NULL)
		pq->tail = NULL;
}

DataType QueueFront(Queue* pq)
{
	assert(pq && !QueueEmpty(pq));

	return pq->head->data;
}

DataType QueueBack(Queue* pq)
{
	assert(pq && !QueueEmpty(pq));

	return pq->tail->data;
}

Queue.h

#pragma once

#include <stdio.h>
#include <stdlib.h>
#include <stdbool.h>
#include <assert.h>

struct BinaryTreeNode;
typedef struct BinaryTreeNode* DataType;

typedef struct QueueNode
{
	DataType data;
	struct QueueNode* next;
}QueueNode;

typedef struct Queue 
{
	struct QueueNode* head;//头指针
	struct QueueNode* tail;//尾指针
}Queue;

//队列初始化
void QueueInit(Queue* pq);
//队列队尾插入
void QueuePush(Queue* pq, DataType x);
//队列销毁
void QueueDestroy(Queue* pq);
//队列队头删除
void QueuePop(Queue* pq);
//判断队列是否为空
bool QueueEmpty(Queue* pq);
//获取队列队头数据值
DataType QueueFront(Queue* pq);
//获取队列队尾数据值
DataType QueueBack(Queue* pq);

以上就是二叉树的遍历以及基础练习了，学习二叉树一定要多画图，很多疑惑都会通过画图解决。希望我的文章对你有所帮助，欢迎👍点赞，📝评论，🌟关注，⭐️收藏

在这里插入图片描述