【算法】判断一个点是否在多边形之内

文章目录

问题背景

在牛客网上遇到这样一个问题：
https://www.nowcoder.com/questionTerminal/fcb839e841a74daab2e442f4dba5b707

题目图片
测试样例

本来觉得挺简单的一道问题，后来发现并不是那么回事……
我们用眼一看就能看明白的事情，怎么写起程序来就变得这么复杂？？？
一时之间又想不出来什么好办法，于是去网上找题解吧。
结果找了一圈，大体知道什么意思了，但是没看见自己满意的，于是琢磨着自己写一篇出来，以便后人乘凉。

先说一句，这其实是个数学问题，只是现在要求我们使用编程语言来写出算法而已。那么，我们需要先想明白这个数学问题怎么做，之后再写程序。

解决思路

网上有很多思路，比如面积法、向量法、角度法、交点个数法。我感觉运算比较方便的是向量法。（这里指的运算方便是指便于计算机计算）

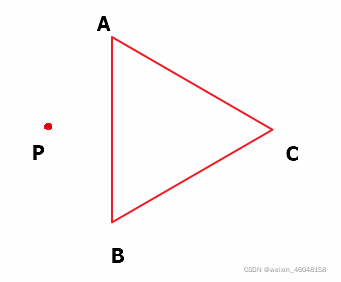
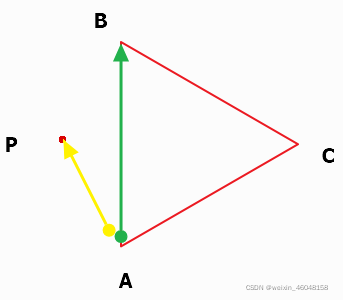
先看看多边形边数 $n = 3$ 的情况，这是个三角形👇

在这里插入图片描述
相信你一眼就能看出来 点P在三角形ABC外部
不过我们如何使用数学的语言来表述这个事实呢？
先假定坐标： $P(x_0, y_0), A(x_1, y_1), B(x_2, y_2), C(x_3, y_3)$

上过大学的同学都知道矢量是可以进行叉乘运算的，比如 $\overrightarrow{AB} × \overrightarrow{AP}$
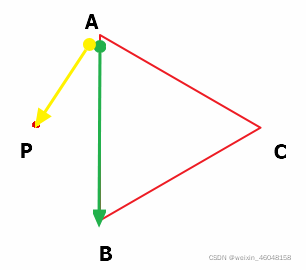
得到的结果是一个向量，这个向量的方向垂直于纸面（也就是图中三角形所在的平面），至于方向具体是向内还是向外，则要看AB与AP的位置关系。我们使用右手定则就可以判断。图中 $A B \times A P$ 的方向是垂直于纸面向内的。
在这里插入图片描述
要是使用行列式来计算 $\overrightarrow{AB} × \overrightarrow{AP}$ 结果的话，大概是这样👇
$\begin{vmatrix} x_2 - x_1 & y_2 - y_1 \\ x_0 - x_1 & y_0 - y_1 \\ \end{vmatrix}$
行列式的计算方法不再赘述，想必大家都会，不会就百度吧。
当然，使用计算机来计算会很快。

我们需要的是这个行列式的结果的正负性，它表现了两个向量的位置关系，如果结果为正，说明第二个向量在第一个向量的逆时针方向，反之，说明第二个向量在第一个向量的顺时针方向

【注意】这里的顺时针和逆时针是从咱们读者的角度观察得到的，也就是正对屏幕向里的方向。另外，顺时针与逆时针的角度都不能大于180度！不然就乱套了，这样的说法也就失效了。

其实也可以换一种说法，使用向量与点的相对位置关系，
将向量AB看作是一个以A为转动中心, B为转动末端的一个指针，

若点P在指针顺时针转动180度以内的方向上，等价于 $\overrightarrow{AB} × \overrightarrow{AP}$ 使用行列式计算的结果 < 0；

若点P在指针逆时针转动180度以内的方向上，等价于 $\overrightarrow{AB} × \overrightarrow{AP}$ 使用行列式计算的结果 > 0；

若点P恰好在向量AB所在的直线上，则行列式的计算结果为0 （向量AB与AP共线）；

严格地讲，两个向量进行叉积运算地结果是向量，不能与数量 0 比较大小，但为了我们讨论问题方便，直接使用行列式的计算结果的正负来代替原来叉积的方向了，请不要dui我.

聪明的读者应该猜到判断的方法了，没错，就是不断计算

$\overrightarrow{AB} × \overrightarrow{AP}$
$\overrightarrow{BC} × \overrightarrow{BP}$
$\overrightarrow{CA} × \overrightarrow{CP}$

如果上面三个式子的正负性相同，说明，点P就在三角形ABC的内部！
需要注意，上面的式子具有轮换对称性，每个式子左边的向量都对应三角形的一条边，而且三个位于式子左边的向量首尾相接正好 “围成一圈”！

我在上面画出的三角形ABC的三个顶点 $A, B, C$ 是逆时针方向分布的，下面再来一个顺时针分布的👇
在这里插入图片描述
这时候 $\overrightarrow{AB} × \overrightarrow{AP}$ 的方向正好与前一种相反！

此时，可以使用计算机进行如下计算,
$\overrightarrow{AB} × \overrightarrow{AP}$ 的结果 > 0 （表示点P在向量AB的左侧）
$\overrightarrow{BC} × \overrightarrow{BP}$ 的结果 < 0 （表示点P在向量BC的右侧）
$\overrightarrow{CA} × \overrightarrow{CP}$ 的结果 < 0 （表示点P在向量CA的右侧）

由于这三个式子最终的结果的正负不一样，我们有理由判定 “点P不在三角形ABC之中”

口诀就是，都在同一侧则在其内，不都在同一侧则在其外

当然，如果某一个式子的结果为0，说明点 P 在三角形的某一条边所在的直线上，
以 $\overrightarrow{AB} × \overrightarrow{AP}$ 的结果 = 0 为例,
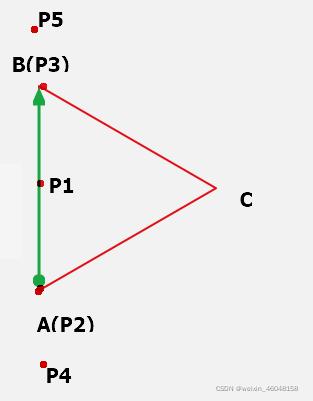
可能有如下的五种情况，
在这里插入图片描述
我们不认为点P1、P2、P3在三角形内部（Inside the triangle），这三个点应该看作是“在三角形上（On the triangle）”的.

至于 P4、P5，则是 “在三角形外（Outside the triangle）”

所以行列式的值为 0 能够推出来两种情况，不能简单认为一定是在三角形外或者上.

好说, 如果 $\leqslant P.x \leqslant B.x$ 或者 $\leqslant P.x \leqslant A.x$ , 说明点 P在线段AB上.

(这里使用横坐标,其实使用纵坐标也是一样的)
(这里突然使用了面向对象的写法, 只是感觉表达效果更好而已, A, B, P都是Point的实例, 都具有横坐标属性x, 各位程序员伙伴们早就见怪不怪了~)

好了, 都到这里了, 其实大家应该能看出来, 上面的方法可以扩展到任意的凸多边形, 凹的不行! ! !

只要给出的点是按逆时针顺序或者顺时针顺序能够组成凸多边形`就行.

关于如何判断一组点的序列是否是按顺时针或者逆时针分布的, 以及这些点是否能够构成凸多边形, 本篇文章不再讨论. 若本篇读者反馈良好, 后续可能会更.

代码实现 C++

注意: 在C++中, 大部分小数的表示是不精确的, 因此, 在比较一个计算结果与 0 的关系时, 通常使用 1e-6来代替 0. 比如, 假设有一个浮点数num, 我们想知道它是不是等于 0, 我们需要这样写 if (abs(num) <= 1e-6) (1e-6就是1乘以10的-6次方); 想知道它是不是小于0, 需要if (num < -1e-6); 想知道它是不是大于0, 需要if (num > 1e-6)

// C++ 代码如下
/*  已知四边形的四个点，求一个点是否在四边形之内的解决方法 */
/*  已知四边形（凸四边形）的四个点A、B、C、D（按逆时针顺序）的坐标，
    求点P是否在ABCD所围成的四边形内，可以通过向量叉乘的方法实现。
 */

#include <iostream>
#include <vector>
#include <algorithm>
using namespace std;

struct Point {
    double x, y;
    Point(double x = 0, double y = 0) : x(x), y(y) {}
    Point operator-(const Point &b) const { // 求向量
        return Point(x - b.x, y - b.y);
    }
    double operator*(const Point &b) const { //叉乘
        return x * b.y - y * b.x;
    }
};

class PointInPolygon {
public:
    bool isPointInPolygon(vector<Point>& points, Point p) {
        int n = points.size();
        int leftcnt = 0; 	// 若点P出现在一个向量的左侧, 则该变量加1
        int rightcnt = 0; 	// 若点P出现在一个向量的右侧, 则该变量加1
        for (int i = 0; i < n; ++i) {
          Point AB = points[(i + 1) % n] - points[i];  // B - A 即为向量 AB
          Point AP = p - points[i];                    // P - A 即为向量 AP
          /* 没想到吧, 其实向量也可以使用点的坐标进行表示!!      */
          auto cross_product = AB * AP;
          if (cross_product > 1e-6) { 
          // 如果向量叉乘大于0，则点p在向量AB的左侧，
          /* 1e-6 是为了避免浮点数的误差*/
            ++leftcnt;
          } else if (cross_product < -1e-6) {	// 点P 在向量AB的右侧
            ++rightcnt;
          }
        }
        return leftcnt == n || rightcnt == n;
    }
};

// 测试用例:
int main() {
    PointInPolygon p;
    vector<Point> points = {Point(0, 0), Point(0, 1), Point(1, 1), Point(1, 0)};
    // 输入的点必须按照 逆时针顺序 或者 顺时针顺序 且能够构成凸多边形, 否则判断结果不正确!

    // Should Output 0
    cout << p.isPointInPolygon(points, Point(-1, -1)) << endl;
    cout << p.isPointInPolygon(points, Point(0, 0)) << endl;
    cout << p.isPointInPolygon(points, Point(1, 1)) << endl;

    // Should Output 1
    cout << p.isPointInPolygon(points, Point(0.5, 0.5)) << endl;
    cout << p.isPointInPolygon(points, Point(0.2, 0.8)) << endl;
    return 0;
}

尾声 & 琐记

凸多边形的性质: 外角和360° (不管有多少条边)
~~继续发展下去可以得到高斯-博内公式~~

任意给出4个点, 不一定能组成凸多边形, 也不一定能组成凹多边形, 如果能组成凹多边形, 不只有一种情况.

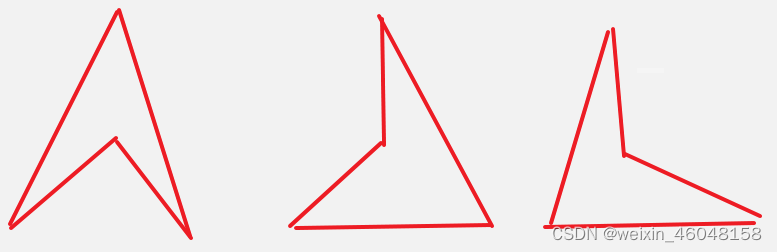
在下面这三张图里, 我已经 “尽力” 表现出了这样一个事实: 给定四个点可以组成凹多边形, 但是有三种情况，凹陷的部分不一样.

凹多边形可以看成是由大的凸多边形扣除小的凸多边形得到的.
在这里插入图片描述

有一篇文章提到利用面积进行四边形的凸凹性判断: https://blog.csdn.net/xinyu391/article/details/92685023

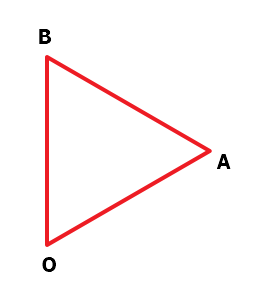
值得注意的是, 求三角形的面积不需要海伦公式. 因为海伦公式适合已知三角形的三条边长求面积, 现在只知道三个点的坐标, 转化成边的长度需要开平方, 计算代价很大. 最好的办法是：使用向量叉积

在这里插入图片描述
$S_\triangle{ABC} = \frac{1}{2}\times |\overrightarrow {OA} \times \overrightarrow {OB}|$

发现了一些有价值的资料：

平面多边形凹凸判断（叉乘法）https://gongjianbo1992.blog.csdn.net/article/details/121413215
凸多边形、凹多边形、凸包算法 https://blog.csdn.net/weixin_43042467/article/details/107029685
判断点是否在给定四边形内的算法 https://jensen-lee.blog.csdn.net/article/details/88718170