1.Dijkstra算法

1.1使用范围

$\bullet$ 寻求从一固定顶点到其余各点的最短路径

$\bullet$ 有向图、无向图和混合图

$\bullet$ 权非负

1.2算法思路

每一次迭代产生一个永久标号，把它接入到以起始点为v₀根的树中，在这棵树上每一个顶点与根结点之间的路径皆为最短路径。

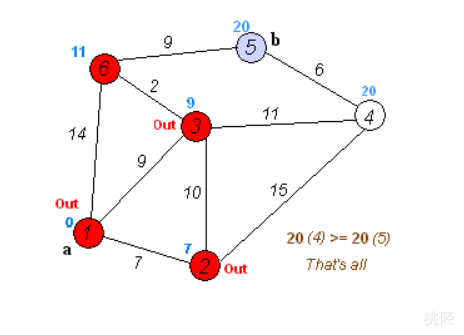
1.3实例

寻找从顶点1到顶点5的最短路径：

一共有六个顶点，生成的带权邻接矩阵为：

$$\left[\begin{array}{cccccc}0& 7& 9& inf& inf& 14\\ 7& 0& 10& 15& inf& inf\\ 9& 10& 0& 11& inf& 2\\ inf& 15& 11& 0& 6& inf\\ inf& inf& inf& 6& 0& 9\\ 14& inf& 2& inf& 9& 0\end{array}\right]$$

2.代码

2.1dijstra函数

function [min,path]=dijkstra(w,start,terminal)
%输入变量w为所求图的带权邻接矩阵，start、terminal分别为路径的起点和终点的编号。
%返回path为从start到termial的最短路径以及长度min

n=size(w,1); label(start)=0; f(start)=start;
%n为所求图的顶点个数，label存放到各点的最短路径，f(v)表示v的父顶点用来还原路径

%初始化将除了start以外的顶点label均设置为无穷大
for i=1:n
    if i~=start
       label(i)=inf;
    end
end

%s数组存放已经搜好的顶点集，初始化只有start
s(1)=start; u=start;
while length(s)<n
    %遍历一遍顶点，将不在顶点集中的顶点选出来进行下面的if判定
    for i=1:n
        ins=0;
        for j=1:length(s)
            if i==s(j)
                ins=1;
            end  
        end
        %判断是否有中继顶点使得它们之间的距离更短，如果有的话更新距离并更新前驱结点
        if ins==0
            v=i;
            if label(v)>(label(u)+w(u,v))
                label(v)=(label(u)+w(u,v)); f(v)=u;
            end 
        end
    end   
    v1=0;
    k=inf;
    %同上再次进行遍历，找到目前最短的路径顶点v1，放入顶点集并改变u的值
    for i=1:n
        ins=0;
        for j=1:length(s)
            if i==s(j)
                ins=1;
            end
        end
        if ins==0
            v=i;
            if k>label(v)
                k=label(v);  v1=v;
            end  
        end
    end
    s(length(s)+1)=v1;  
    u=v1;
end

min=label(terminal); path(1)=terminal;
i=1; 

%按倒序结果推出最短路径
while path(i)~=start
    path(i+1)=f(path(i));
    i=i+1 ;
end
path(i)=start;
L=length(path);
%翻转得到最短路径
path=path(L:-1:1);

2.2调用函数

w = [0,7,9,inf,inf,14;
     7,0,10,15,inf,inf;
     9,10,0,11,inf,2;
     inf,15,11,0,6,inf;
     inf,inf,inf,6,0,9;
     14,inf,2,inf,9,0];
 start=1;terminal=5;
[min,path]=dijkstra(w,start,terminal);
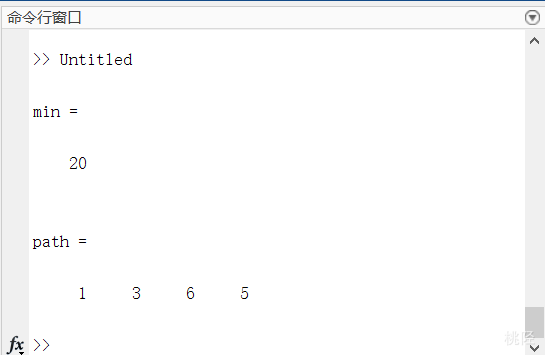
min,path

结果：