文章目录
第二节 二叉树
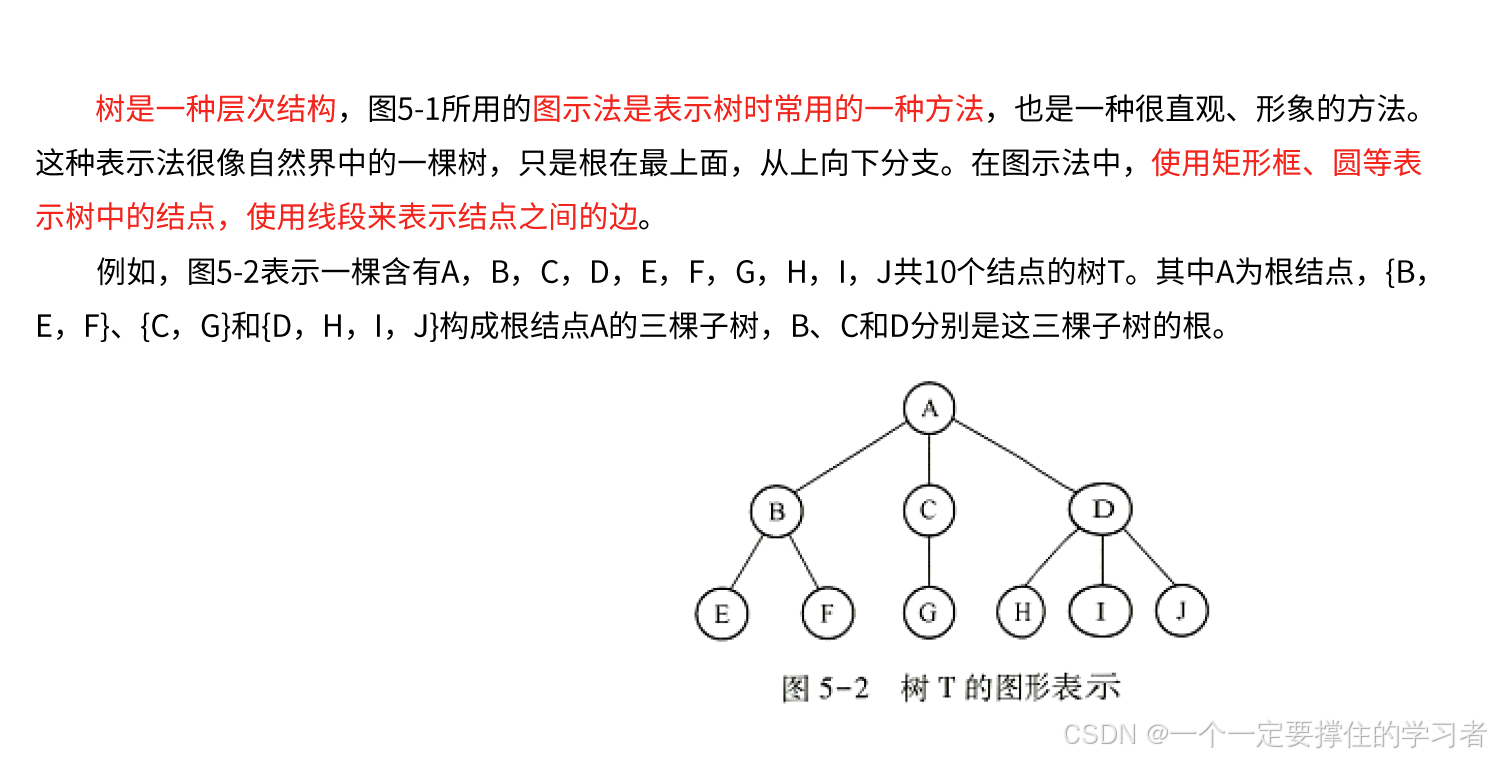
二叉树的定义及重要性质
二叉树是结点的一个有限集合,这个集合或者为空,或者由一个根结点以及两棵互不相交的、定义5-2分别称为这个根的左子树和右子树的二叉树组成。左子树和右子树的根分别称为此二叉树根结点的左子结点和右子结点。
二叉树的左子树和右子树都可以存在或者为空,不同的存在状态可以组合出5种基本形态,即两棵子树均为空或均不为空,或者一棵为空、另一棵不为空,还有空树。这5种形态如图5-3所示。
叉树与树有什么关系呢?二叉树允许有空树,而树中至少含有一个结点。从这个方面来看,二叉树并不是树的真子集。除此之外,在概念上,树与二叉树之间也存在差异。对一般的非有序树而言,每个结点的各个子结点之间没有次序,而二叉树中每个结点的子结点都规定了左、右次序。即使是有序树,它与二叉树也略有不同。例如,若有序树中某个结点只有一个子结点,那么这个子结点是其父结点的唯一孩子。但在二叉树中,如果某个结点有一个子结点,那么它可以是其父结点的左子结点,也可以是其右子结点,由此可以对应于两种不同的二叉树树形。例如,图5-3c与图5-3d是两棵完全不同的二叉树。
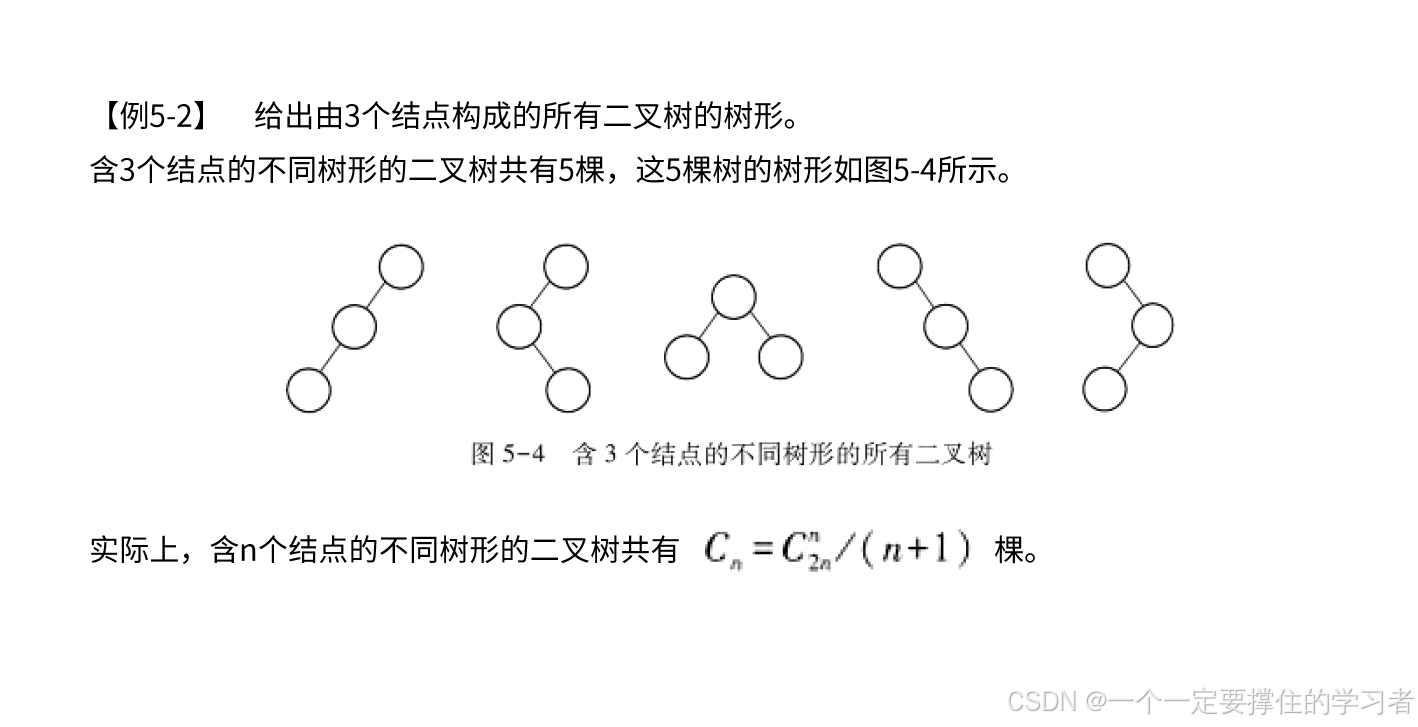
n个结点,能组合成多少个不同的二叉树
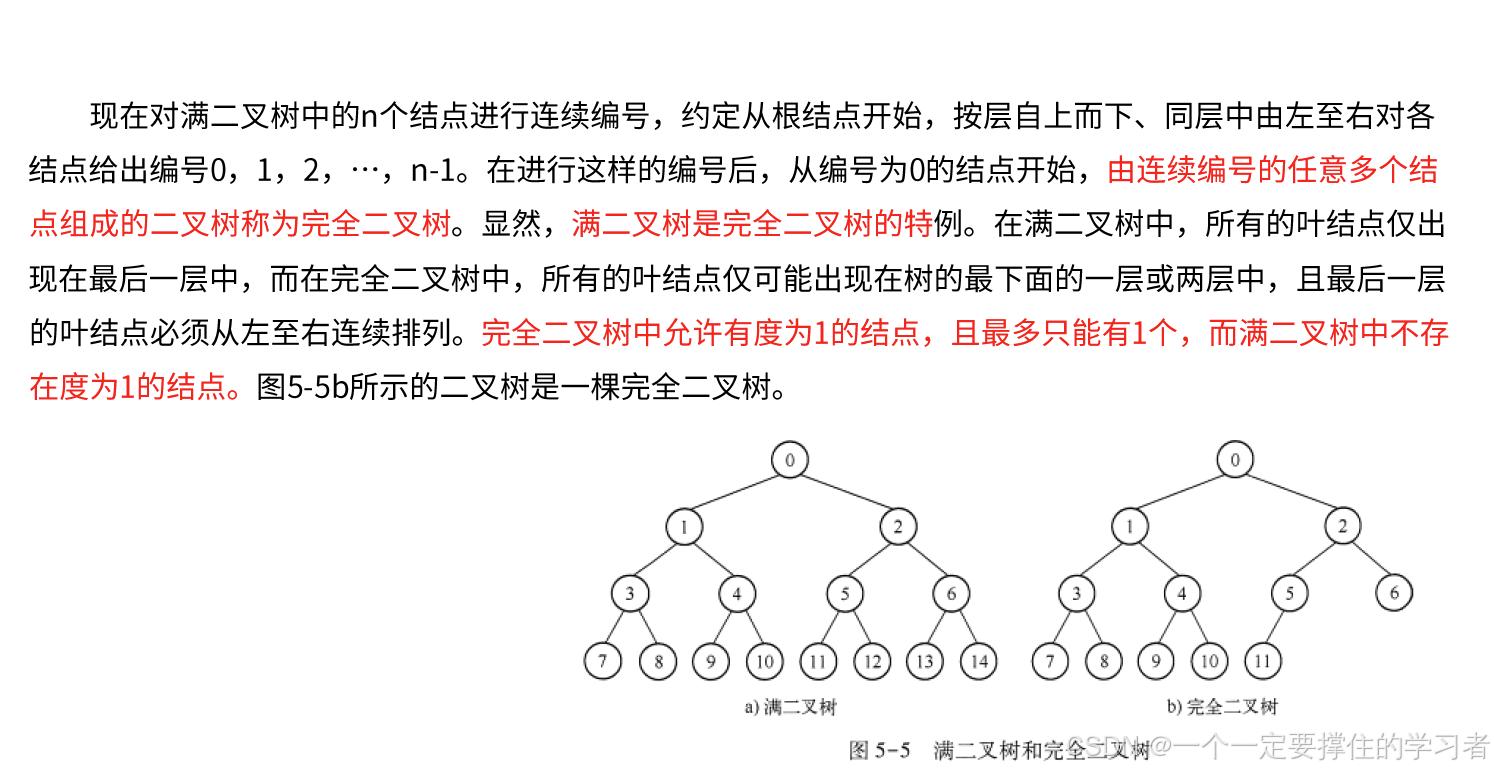
满二叉树、完全二叉树
完全二叉树的性质
二叉树的性质
二叉树的结点数
这个性质的含义是,二叉树中叶结点的个数仅与度为2的结点的个数有关,具体来说,叶结点的个数比度为2的结点的个数多1,而与度为1的结点个数无关。
仅增加或减少二叉树中度为1的结点,对二叉树中叶结点的个数没有影响。这个性质也称为满二叉树定理。
完全二叉树的高度
二叉树的存储
与线性表类似,二叉树也有两种存储方式,即顺序存储方式和链式存储方式。
顺序存储方式
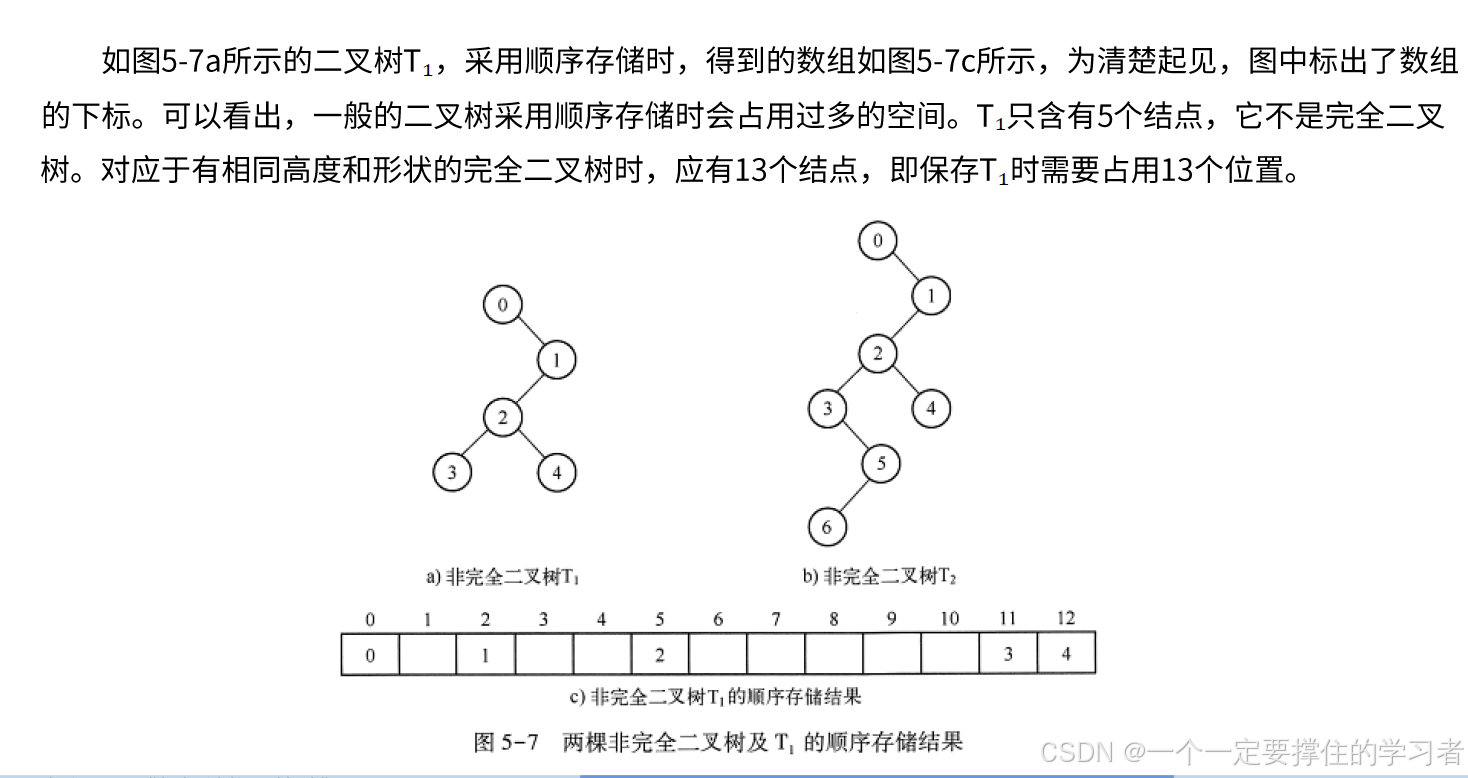
先看看特殊的完全二叉树的存储方法。根据完全二叉树的定义,除最后一层以外,其余各层都是满的,而且最后一层的结点自左至右紧密排列。所以,可以使用一维数组依次存储树中各层的各个结点。存储的规则是,各层自上至下、同层间自左至右,将结点依次存入数组从前至后的各个元素中。按照前面使用过的编号方法,编号为i的结点存放在数组中下标为i的位置。例如,图5-5b所示的完全二叉树可以使用具有至少12个元素的一维数组存储,存放的结果如图5-6所示。
基于这样的存储规则保存的二叉树,可以很方便地在数组中找到二叉树中的相关结点,即若知道二叉树某一结点在数组中的保存位置,则可以计算出其父结点(若存在)和左、右子结点(若存在)在数组中的保存位置。
对于一般的二叉树,顺序存储的思想是,针对二叉树中的每个位置,无论这个位置有没有结点,都在数组中预留保存单元。在采用这种存储方式保存完全二叉树时,既不浪费空间,又便于有关操作的实现。
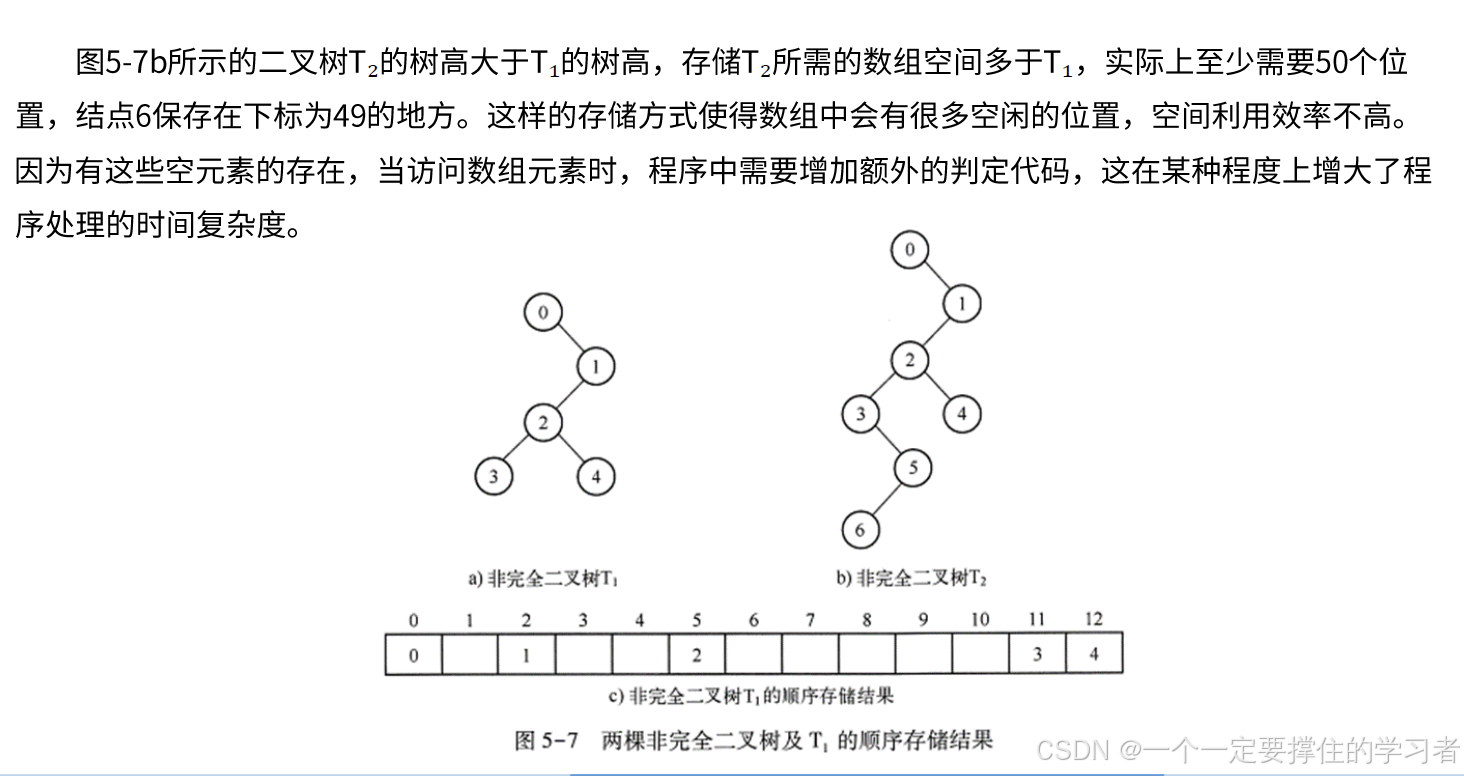
但是,如果使用这样的存储规则保存一般的二叉树,则可能会出现空间浪费的情况。
链式存储方式
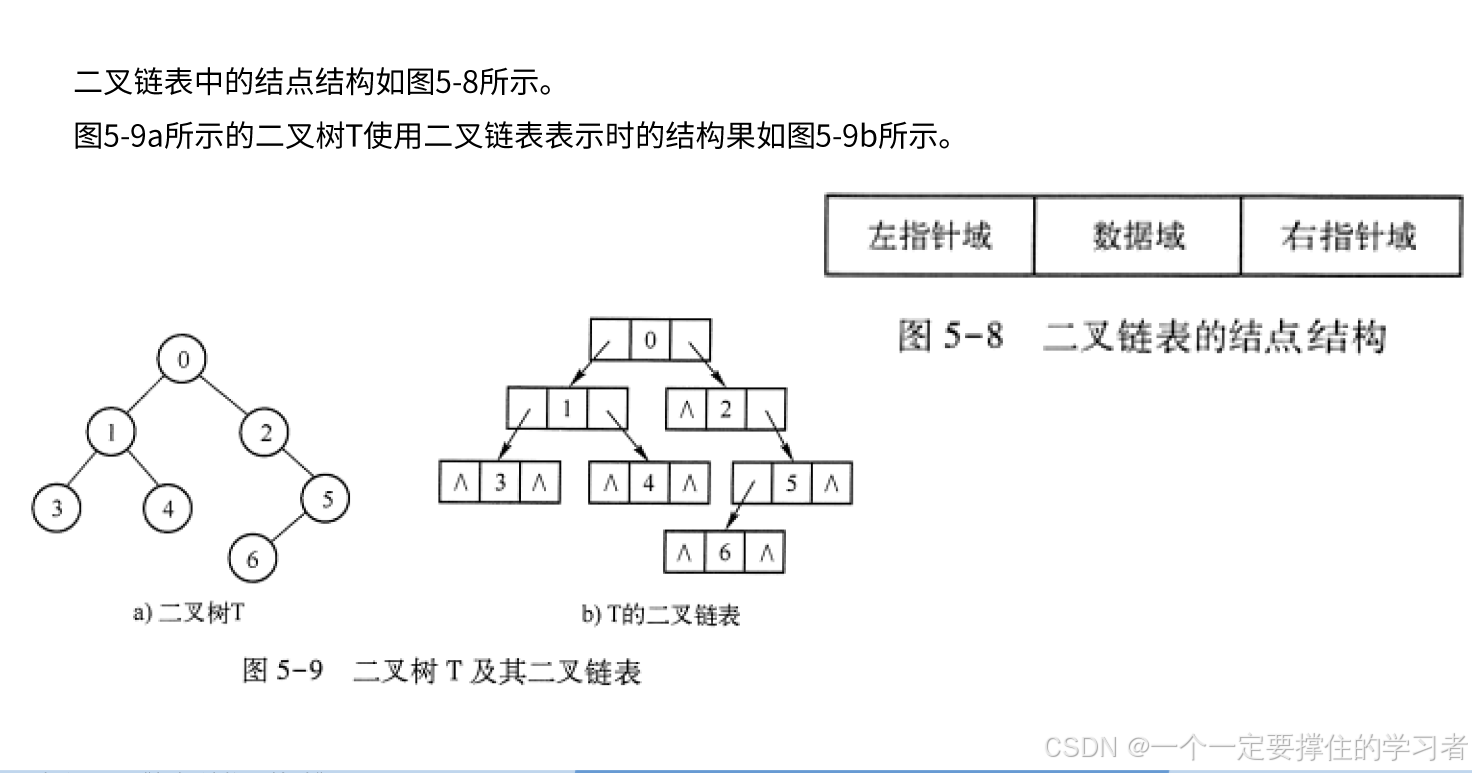
与二叉树的顺序存储方式相对应的是它的链式存储方式。钱链式存储结构与二又树的实际逻辑结构更加吻合,非常适合于表示二又树。
二叉树的定义规定,每个结点最多有两个子结点,分别是它的左子结点和右子结点。据此,可以这样定义一个结点结构:它含有两个指针域,一个指针用来指向该结点左子结点所在的结点,称为左孩子指针,简称为左指针;另一个指针用来指向该结点右子结点所在的结点,称为右孩子指针,简称为右指针。此外,还定义一个用来保存结点中数据的数据域。所以,每个结点至少包含3个域,分别保存数据、左指针和右指针。由于每个结点都含有两个指针域,故这样的链式结构被形象地称为二叉链表结构。回忆一下,在双向链表中每个结点也含有两个指针域和一个数据域。请考生考虑,使用相同的结点结构构造的双向链表和二叉链表有什么不同?