文章目录
ConFEDE:用于多模态情感分析的对比特征分解
总结:提出了一种对比特征分解框架 ConFEDE,基于对比特征分解,利用对比训练损失,捕捉了不同模态之间、不同样本之间的一致性和差异性。
文章信息
作者:Jiuding Yang,weidong guo
单位:University of Alberta(艾伯塔大学,加拿大)
会议/期刊:Proceedings of the 61st Annual Meeting of the Association for Computational Linguistics (ACL 2023)(CCF A)
题目:ConFEDE: Contrastive Feature Decomposition for Multimodal Sentiment Analysis
年份:2023
研究目的
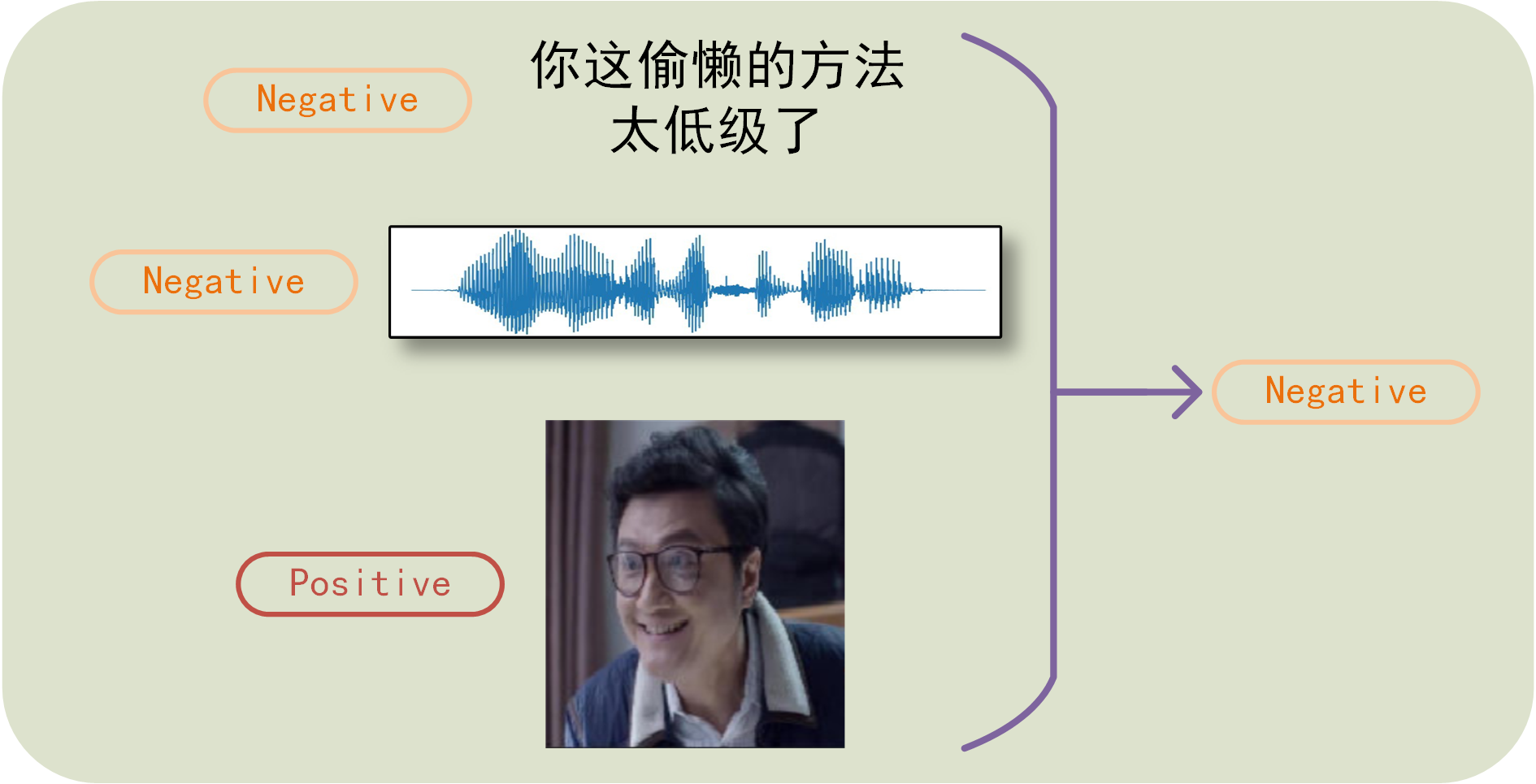
不同的模态之间识别的情感可能是不同的,不同情感的模态可能完全改变整体情感的含义,整体情感不能简单地通过所有模态中的多数投票来判断。因此模态间一致性与差异性方面的多模态表征学习是非常有必要的。
研究内容
- 将样本间对比学习和样本内模态分解整合为一个简单统一的损失函数,该函数基于一个定制的数据采样器,对正/负数据对进行采样,以执行这两项学习任务。
- 将每个模态分解为一个相似性特征(similarity feature)和一个相异性特征(dissimilarity feature),并以文本的相似性特征为锚,建立所有分解特征之间的对比关系。(主要贡献)
- 引入了依赖于每个分解后的模态表征的多任务预测损失,使模型能够同时从多模态预测和单模态预测中学习。
研究方法
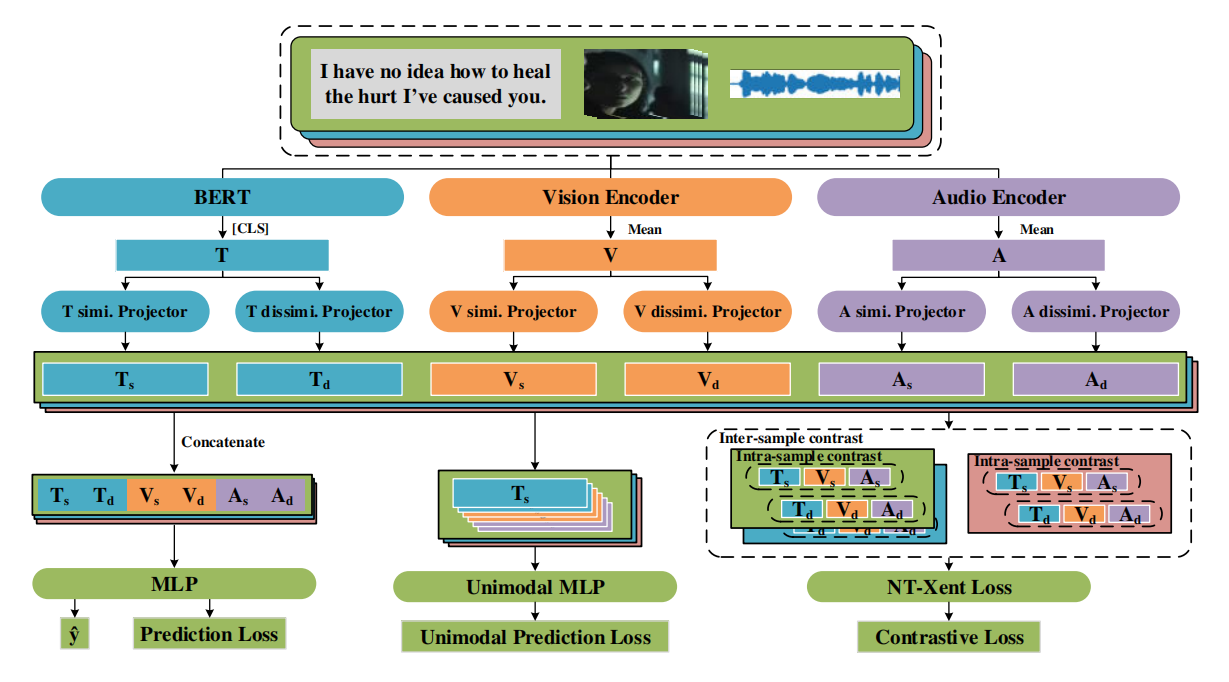
1.总体结构
对于数据集中的每一个样本,首先用相应的特征提取器对每种模态特征进行编码,提取相应模态的初始特征。(文本模态使用 BERT 的 [CLS] 标签对文本信息编码,视觉和音频模态使用两个 transformer 的编码器进行编码)
然后,利用不同的投影器将每个模态的初始特征( T , V , A T,V,A T,V,A)分解为相似性特征( T s , V s , A s T_s,V_s,A_s Ts,Vs,As)和相异性特征( T d , V d , A d T_d,V_d,A_d Td,Vd,Ad)。(每个投影器都由 layer normalization,带有 Tanh 激活函数的linear layer 以及 dropout layer 构成)
最后,通过对比特征分解学习不断地更新这六个分解特征,并将其融合到 ConFEDE 模型中,利用多任务学习目标损失函数进行训练。
2.损失函数
总体损失:
L
a
l
l
=
L
p
r
e
d
+
β
u
n
i
L
u
n
i
+
β
c
l
L
c
l
\mathcal{L}_{\mathrm{all}}=\mathcal{L}_{\mathrm{pred}}+\beta_{\mathrm{uni}}\mathcal{L}_{\mathrm{uni}}+\beta_{\mathrm{cl}}\mathcal{L}_{\mathrm{cl}}
Lall=Lpred+βuniLuni+βclLcl
| 符号 | 含义 |
|---|---|
| L p r e d \mathcal{L}_{\mathrm{pred}} Lpred | 多模态预测损失 |
| L u n i \mathcal{L}_{\mathrm{uni}} Luni | 单模态预测损失 |
| L c l \mathcal{L}_{\mathrm{cl}} Lcl | 对比损失 |
| β c l , β u n i \beta_{cl},\beta_{uni} βcl,βuni | 超参数 |
多模态预测损失 L p r e d \mathcal{L}_{\mathrm{pred}} Lpred:(平均绝对误差)
将所有6个分解的模态特征进行合并,得到分类器的输入
[
T
s
i
;
T
d
i
;
V
s
i
;
V
d
i
;
A
s
i
;
A
d
i
]
[\mathbf{T}_s^i;\mathbf{T}_d^i;\mathbf{V}_s^i;\mathbf{V}_d^i;\mathbf{A}_s^i;\mathbf{A}_d^i]
[Tsi;Tdi;Vsi;Vdi;Asi;Adi](使用带有 ReLU 激活函数的多层感知器(MLP)作为分类器)通过分类器获取最终的分类结果
y
^
\hat{y}
y^ 。
y
^
m
i
=
M
L
P
(
[
T
s
i
;
V
s
i
;
A
s
i
;
T
d
i
;
V
d
i
;
A
d
i
]
)
,
L
p
r
e
d
=
1
n
∑
i
=
1
n
(
y
m
i
−
y
^
m
i
)
2
,
\begin{gathered}\hat{y}_m^i=\mathsf{MLP}([\mathbf{T}_s^i;\mathbf{V}_s^i;\mathbf{A}_s^i;\mathbf{T}_d^i;\mathbf{V}_d^i;\mathbf{A}_d^i]),\\\\\mathcal{L}_{\mathbf{pred}}=\frac1n\sum_{i=1}^n(y_m^i-\hat{y}_m^i)^2,\end{gathered}
y^mi=MLP([Tsi;Vsi;Asi;Tdi;Vdi;Adi]),Lpred=n1i=1∑n(ymi−y^mi)2,
| 符号 | 含义 |
|---|---|
| [ ⋅ ; ⋅ ] [\cdot;\cdot] [⋅;⋅] | 表示concatenate操作 |
| B B B | 表示一个批次 |
| y ^ m i \hat{y}_m^i y^mi | 多模态预测标签 |
| y m i y_m^i ymi | 多模态真实标签 |
| n n n | 一个批次中样本的数量 |
单模态预测损失 L u n i \mathcal{L}_{\mathrm{uni}} Luni:
对于每个样本 i i i,将 6 个分解的特征分别输入一个权重共享的 MLP 分类器,得到 6 个预测结果。(相似性特征 T s i , V s i , A s i T_s^i,V_s^i,A_s^i Tsi,Vsi,Asi 通过 MLP 映射来预测多模态标签 y m i y_m^i ymi,相异性特征 T d i , V d i , A d i T_d^i,V_d^i,A_d^i Tdi,Vdi,Adi 通过 MLP 映射来预测特定模态标签 y t i , y v i , y a i y_t^i,y_v^i,y_a^i yti,yvi,yai ,但是当特定模态标签没有的时候,例如MOSI与MOSEI数据集,相异性特征 T d i , V d i , A d i T_d^i,V_d^i,A_d^i Tdi,Vdi,Adi 也被用来预测多模态标签 y m i y_m^i ymi )
原理:让相似性特征
T
s
i
,
V
s
i
,
A
s
i
T_s^i,V_s^i,A_s^i
Tsi,Vsi,Asi 通过样本的整体多模态标签捕获不同模态之间共享的一致信息,让相异性特征
T
d
i
,
V
d
i
,
A
d
i
T_d^i,V_d^i,A_d^i
Tdi,Vdi,Adi 保留由单模态标签表示的特定模态信息。
u
^
i
=
M
L
P
(
[
T
s
i
,
V
s
i
,
A
s
i
,
T
d
i
,
V
d
i
,
A
d
i
]
)
,
u
i
=
[
y
m
i
,
y
m
i
,
y
m
i
,
y
t
i
,
y
v
i
,
y
a
i
]
,
L
u
n
i
=
1
n
∑
i
=
1
n
∥
u
i
−
u
^
i
∥
2
2
,
\begin{gathered} \hat{\boldsymbol{u}}^i=\mathrm{MLP}([\mathbf{T}_s^i,\mathbf{V}_s^i,\mathbf{A}_s^i,\mathbf{T}_d^i,\mathbf{V}_d^i,\mathbf{A}_d^i]), \\ \\ \boldsymbol{u}^i=[y_m^i,y_m^i,y_m^i,y_t^i,y_v^i,y_a^i], \\ \\ \mathcal{L}_{\mathbf{uni}}=\frac1n\sum_{i=1}^n\|\boldsymbol{u}^i-\hat{\boldsymbol{u}}^i\|_2^2, \end{gathered}
u^i=MLP([Tsi,Vsi,Asi,Tdi,Vdi,Adi]),ui=[ymi,ymi,ymi,yti,yvi,yai],Luni=n1i=1∑n∥ui−u^i∥22,
| 符号 | 含义 |
|---|---|
| u ^ i \hat{u}^i u^i | 预测标签 |
| u i u^i ui | 真实标签 |
对比损失 L c l \mathcal{L}_{\mathrm{cl}} Lcl:
在一个简单的联合对比损失中进行对比:相似样本与相异样本进行对比;同一样本相似特征与相异特征进行对比。
L
c
l
=
1
n
∑
i
=
1
n
ℓ
c
l
i
,
\mathcal{L}_{cl}=\frac1n\sum_{i=1}^n\ell_{cl}^i,
Lcl=n1i=1∑nℓcli,
ℓ c 1 i = ∑ ( a , p ) ∈ P i − log exp ( s i m ( a , p ) / τ ) ∑ ( a , k ) ∈ N i ∪ P i exp ( s i m ( a , k ) / τ ) , \ell_{\mathbf{c}1}^i=\sum_{(\boldsymbol{a},\boldsymbol{p})\in\mathcal{P}^i}-\log\frac{\exp(\mathbf{sim}(\boldsymbol{a},\boldsymbol{p})/\tau)}{\sum_{(\boldsymbol{a},\boldsymbol{k})\in\mathcal{N}^i\cup\mathcal{P}^i}\exp(\mathbf{sim}(\boldsymbol{a},\boldsymbol{k})/\tau)}, ℓc1i=(a,p)∈Pi∑−log∑(a,k)∈Ni∪Piexp(sim(a,k)/τ)exp(sim(a,p)/τ),
| 符号 | 含义 |
|---|---|
| ℓ c l i \ell_{cl}^i ℓcli | 代表样本 i i i 的对比损失 |
| ( a , p ) 、 ( a , k ) (a,p)、(a,k) (a,p)、(a,k) | 表示一对分解后的特征向量。可以是一个样本内的特征向量,如
(
T
s
i
,
V
s
i
)
、
(
T
s
i
,
A
d
i
)
(T_s^i,V_s^i)、(T_s^i,A_d^i)
(Tsi,Vsi)、(Tsi,Adi);也可以是不同样本间的特征向量,如
(
T
s
i
,
T
s
j
)
(T_s^i,T_s^j)
(Tsi,Tsj) 注意: ( a , p ) ∈ P i (a,p) \in \mathcal{P}^i (a,p)∈Pi, ( a , k ) ∈ P i o r N i (a,k) \in \mathcal{P}^i\; or\; \mathcal{N}^i (a,k)∈PiorNi |
| P i \mathcal{P}^i Pi | 正对集合,包括样本内正对
P
i
n
t
r
a
i
\mathcal{P}_\mathrm{intra}^i
Pintrai和样本间正对
P
i
n
t
e
r
i
\mathcal{P}_\mathrm{inter}^i
Pinteri P i = P i n t r a i ∪ P i n t e r i \mathcal{P}^i=\mathcal{P}_\mathrm{intra}^i\cup\mathcal{P}_\mathrm{inter}^i Pi=Pintrai∪Pinteri |
| N i \mathcal{N}^i Ni | 负对集合,包括样本内负对
N
i
n
t
r
a
i
\mathcal{N}_\mathrm{intra}^i
Nintrai和样本间负对
N
i
n
t
e
r
i
\mathcal{N}_\mathrm{inter}^i
Ninteri N i = N i n t r a i ∪ N i n t e r i \mathcal{N}^i=\mathcal{N}_\mathrm{intra}^i\cup\mathcal{N}_\mathrm{inter}^i Ni=Nintrai∪Ninteri |
3.Data Sampler
数据采样器(Data Sampler)根据多模态特征和多模态标签检索给定样本的相似样本,从而在样本间执行有监督的对比学习。采样过程如下:
- 首先给定包含 ∣ D ∣ |D| ∣D∣个样本的数据集 D,对于 D 中的每个样本对 ( i , j ) (i,j) (i,j),计算它们之间的余弦相似度得分。
C i , j = s i n ( [ T i ; V i ; A i ] , [ T j ; V j ; A j ] ) , sim ( w , v ) = w T v / ∣ ∣ w ∣ ∣ ⋅ ∣ ∣ v ∣ ∣ \mathcal{C}^{i,j}=\mathsf{sin}([\mathbf{T}^i;\mathbf{V}^i;\mathbf{A}^i],[\mathbf{T}^j;\mathbf{V}^j;\mathbf{A}^j]),\\ \\ \operatorname{sim}(\boldsymbol{w},\boldsymbol{v})=\boldsymbol{w}^T\boldsymbol{v}/||\boldsymbol{w}||\cdot||\boldsymbol{v}|| Ci,j=sin([Ti;Vi;Ai],[Tj;Vj;Aj]),sim(w,v)=wTv/∣∣w∣∣⋅∣∣v∣∣
| 符号 | 含义 |
|---|---|
| sim ( w , v ) \operatorname{sim}(\boldsymbol{w},\boldsymbol{v}) sim(w,v) | 表示向量 w w w 与向量 v v v 之间的余弦相似度 |
| [ ⋅ ; ⋅ ] [\cdot;\cdot] [⋅;⋅] | 表示concatenate操作 |
| T , V , A T,V,A T,V,A | 分别代表模态各自的初始模态特征 |
- 然后,检索每个样本的候选相似/相异样本集。对于每个样本 i i i ,根据相似度得分从高到低将具有相同多模态标签 y m i y_m^i ymi 的样本排序,作为候选相似样本集 S 0 i S_0^i S0i 。将标签 y m i y_m^i ymi 以外的样本排序,作为候选相异样本集 S 1 i S_1^i S1i 。
从候选相似样本集 S 0 i S_0^i S0i 中随机选取两个余弦相似度得分较高的近似样本,与样本 i i i 构成样本间正对,记为 N e i g h b o r i \mathrm{Neighbor}^i Neighbori;从候选相异样本集 S 1 i S_1^i S1i 中随机选取四个不同的样本组成样本间负对,记为 O u t l i e r i \mathrm{Outlier}^i Outlieri(其中两个样本 O u t l i e r 1 i \mathrm{Outlier}^i_1 Outlier1i具有较低的余弦相似度分数,另外两个样本 O u t l i e r 2 i \mathrm{Outlier}^i_2 Outlier2i具有较高的余弦相似度分数)。
为什么这样选择?通常倾向于选择 N e i g h b o r i \mathrm{Neighbor}^i Neighbori与 O u t l i e r 1 i \mathrm{Outlier}^i_1 Outlier1i中的样本分别与样本 i i i 形成正对和负对。但是由于 O u t l i e r 2 i \mathrm{Outlier}^i_2 Outlier2i中的样本与样本 i i i 具有不同的标签,并且具有相似的语义信息,所以 O u t l i e r 2 i \mathrm{Outlier}^i_2 Outlier2i中的样本很难与样本 i i i 区分开。故,将 O u t l i e r 2 i \mathrm{Outlier}^i_2 Outlier2i中的样本也添加到 O u t l i e r i \mathrm{Outlier}^i Outlieri中。通过对比学习让 O u t l i e r 2 i \mathrm{Outlier}^i_2 Outlier2i 中的样本与样本 i i i 区分开。
4.数据采样算法
5.Contrastive Feature Decomposition(重点)
使用了将样本内对比学习和样本间对比学习统一的一个 NT-Xent 对比损失框架,同时进行模态表征学习和模态分解。
ℓ
c
1
i
=
∑
(
a
,
p
)
∈
P
i
−
log
exp
(
s
i
m
(
a
,
p
)
/
τ
)
∑
(
a
,
k
)
∈
N
i
∪
P
i
exp
(
s
i
m
(
a
,
k
)
/
τ
)
,
\ell_{\mathbf{c}1}^i=\sum_{(\boldsymbol{a},\boldsymbol{p})\in\mathcal{P}^i}-\log\frac{\exp(\mathbf{sim}(\boldsymbol{a},\boldsymbol{p})/\tau)}{\sum_{(\boldsymbol{a},\boldsymbol{k})\in\mathcal{N}^i\cup\mathcal{P}^i}\exp(\mathbf{sim}(\boldsymbol{a},\boldsymbol{k})/\tau)},
ℓc1i=(a,p)∈Pi∑−log∑(a,k)∈Ni∪Piexp(sim(a,k)/τ)exp(sim(a,p)/τ),
P i = P i n t r a i ∪ P i n t e r i , N i = N i n t r a i ∪ N i n t e r i . \begin{aligned}\mathcal{P}^i&=\mathcal{P}_\mathrm{intra}^i\cup\mathcal{P}_\mathrm{inter}^i,\\ \\ \mathcal{N}^i&=\mathcal{N}_\mathrm{intra}^i\cup\mathcal{N}_\mathrm{inter}^i.\end{aligned} PiNi=Pintrai∪Pinteri,=Nintrai∪Ninteri.
样本内的正对/负对构建:
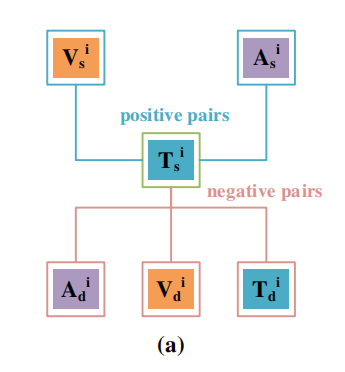
使用六个分解特征( T s , V s , A s , T d , V d , A d \mathbf{T}_s,\mathbf{V}_s,\mathbf{A}_s,\mathbf{T}_d,\mathbf{V}_d,\mathbf{A}_d Ts,Vs,As,Td,Vd,Ad)形成样本内的正/负对。选择文本相似性特征 T s i T_s^i Tsi作为锚点,使视觉和听觉相似性特征 V s i V_s^i Vsi 与 A s i A_s^i Asi 向 T s i T_s^i Tsi 靠拢,同时将所有模态中的相异性特征 T d i , V d i , A d i T_d^i,V_d^i,A_d^i Tdi,Vdi,Adi 远离 T s i T_s^i Tsi 。
P
i
n
t
r
a
i
=
{
(
T
s
i
,
V
s
i
)
,
(
T
s
i
,
A
s
i
)
}
∪
{
(
T
s
j
,
V
s
j
)
,
(
T
s
j
,
A
s
j
)
∣
j
∈
Neighbor
i
∪
Outlier
i
}
,
N
i
n
t
r
a
i
=
{
(
T
s
i
,
T
d
i
)
,
(
T
s
i
,
V
d
i
)
,
(
T
s
i
,
A
d
i
)
}
∪
{
(
T
s
j
,
T
d
j
)
,
(
T
s
j
,
V
d
j
)
,
(
T
s
j
,
A
d
j
)
∣
j
∈
Neighbor
i
∪
Outlier
i
}
,
\begin{aligned} &\mathcal{P}_{\mathrm{intra}}^{i}= \{(\mathbf{T}_s^i,\mathbf{V}_s^i),(\mathbf{T}_s^i,\mathbf{A}_s^i)\} \cup\{(\mathbf{T}_s^j,\mathbf{V}_s^j),(\mathbf{T}_s^j,\mathbf{A}_s^j) \quad| \quad j\in\text{Neighbor}^i\cup\text{Outlier}^i\}, \\ \\ &\mathcal{N}_{\mathrm{intra}}^i= \{(\mathbf{T}_s^i,\mathbf{T}_d^i),(\mathbf{T}_s^i,\mathbf{V}_d^i),(\mathbf{T}_s^i,\mathbf{A}_d^i)\} \cup\{(\mathbf{T}_s^j,\mathbf{T}_d^j),(\mathbf{T}_s^j,\mathbf{V}_d^j),(\mathbf{T}_s^j,\mathbf{A}_d^j) \\ &\qquad\qquad\qquad\qquad\qquad\qquad\qquad\qquad\qquad\qquad\qquad\quad | \quad j\in\text{Neighbor}^i\cup\text{Outlier}^i\}, \end{aligned}
Pintrai={(Tsi,Vsi),(Tsi,Asi)}∪{(Tsj,Vsj),(Tsj,Asj)∣j∈Neighbori∪Outlieri},Nintrai={(Tsi,Tdi),(Tsi,Vdi),(Tsi,Adi)}∪{(Tsj,Tdj),(Tsj,Vdj),(Tsj,Adj)∣j∈Neighbori∪Outlieri},
注意:
N
e
i
g
h
b
o
r
i
\mathrm{Neighbor}^i
Neighbori与
O
u
t
l
i
e
r
i
\mathrm{Outlier}^i
Outlieri分别代表样本
i
i
i 的相似样本和相异样本,
j
∈
Neighbor
i
∪
Outlier
i
j\in\text{Neighbor}^i\cup\text{Outlier}^i
j∈Neighbori∪Outlieri 所起的作用是扩大对比范围。
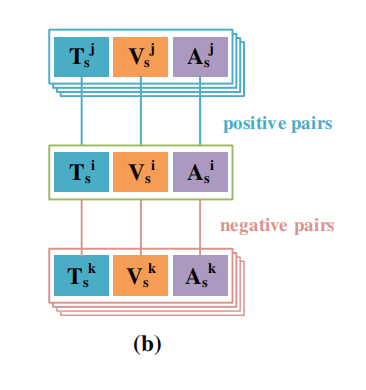
样本间的正对/负对构建:
根据数据采样器采样得到的 N e i g h b o r i \mathrm{Neighbor}^i Neighbori与 O u t l i e r i \mathrm{Outlier}^i Outlieri构建样本间的正对/负对。
P
i
n
t
e
r
i
=
{
(
T
s
i
,
T
s
j
)
,
(
V
s
i
,
V
s
j
)
,
(
A
s
i
,
A
s
j
)
∣
j
∈
Neighbor
i
}
N
i
n
t
e
r
i
=
{
(
T
s
i
,
T
s
k
)
,
(
V
s
i
,
V
s
k
)
,
(
A
s
i
,
A
s
k
)
∣
k
∈
Outlier
i
}
.
\begin{aligned} \mathcal{P}_{\mathrm{inter}}^i=& \{(\mathbf{T}_s^i,\mathbf{T}_s^j),(\mathbf{V}_s^i,\mathbf{V}_s^j),(\mathbf{A}_s^i,\mathbf{A}_s^j) \quad | \quad j\in\text{Neighbor}^i\} \\ \\ \mathcal{N}_{\mathrm{inter}}^i=& \{(\mathbf{T}_s^i,\mathbf{T}_s^k),(\mathbf{V}_s^i,\mathbf{V}_s^k),(\mathbf{A}_s^i,\mathbf{A}_s^k) \quad | \quad k\in\text{Outlier}^i\}. \end{aligned}
Pinteri=Ninteri={(Tsi,Tsj),(Vsi,Vsj),(Asi,Asj)∣j∈Neighbori}{(Tsi,Tsk),(Vsi,Vsk),(Asi,Ask)∣k∈Outlieri}.
注意:只使用相似性特征来获得样本间的配对,因为同一类别中相似性样本的相似性特征应该很接近,而不同类别中样本的相似性特征应该相距较远。
结果与讨论
⚠ 斜体是消融实验
- 将 ConFEDE 与一些 SOTA 模型进行对比。在 CH-SIMS 数据集上 ConFEDE 的大多数性能都是 SOTA 的结果,在 CH-MOSI 与 CH-MOSEI 数据集上,ConFEDE 的性能在多个指标下也表现出了不错的效果。
- 通过去除样本间对比学习和样本内对比学习,来进行消融研究,表明了样本间对比学习和样本内对比学习的有效性,证明了样本内对比学习可以很好的过滤视觉和音频模态中的噪声,样本间对比学习可以学习到样本之间的共同信息和不同信息。
- 在去除了样本间对比学习的基础上(只剩下样本内对比学习),设置了三组消融实现,分别是仅使用多模态标签进行单模态预测的 Intra、不含单模态预测组件的 Intra、不含相似性-相异性学习方法的 Intra。通过实验表明了 ConFEDE 的每个组件都是有效的,所有的设置都是有必要的。
- 通过设置使用所有相似性特征作为锚点的样本内对比学习的消融实验,表明了使用视觉模态和音频模态作为锚点,会引入更多的噪声,从而削弱了对比特征分解学习的去噪能力。证明了仅使用文本模态作为锚点的合理性。
- 通过可视化经过 ConFEDE 的分解特征与未经过 ConFEDE 的分解特征,表明了对比特征分解是有效的,并且 ConFEDE 可以学习到模态之间的一致性与不一致性。
代码和数据集
代码:https://github.com/XpastaX/ConFEDE
数据集:CMU-MOSI,CMU-MOSEI,CH-SIMS
实验环境:NVIDIA RTX 3090(24G)
附录
余弦相似度值越大,表示两个向量越相似。
余弦相似度的值越大越好。在余弦相似度中,值的范围在-1到1之间,其中1表示完全相似,-1表示完全不相似,0表示没有相似性。因此,当余弦相似度接近1时,表示两个向量在方向上非常接近,即它们之间的夹角非常小,从而意味着它们更相似。相反,当余弦相似度接近-1时,表示两个向量在方向上完全相反,因此它们是完全不相似的。所以,余弦相似度的值越大,两个向量就越相似。
😃😃😃