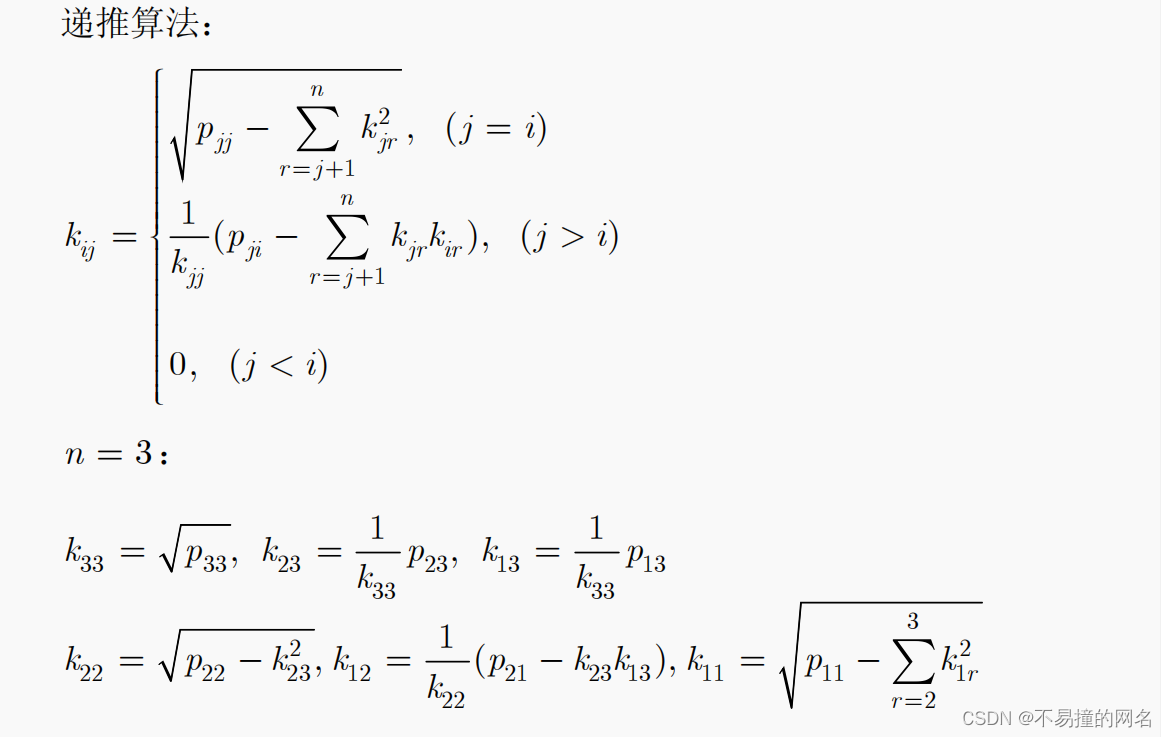正定对称矩阵的Cholesky分解是一种特殊的矩阵分解方法，它将一个正定对称矩阵 (A) 分解为一个下三角矩阵 (K) 和其转置 (K^T) 的乘积$$即A=K{K}^T$$
这里，矩阵 (K) 的对角元素都是正数。Cholesky分解在解决线性方程组、计算矩阵的逆以及进行数值优化等问题中非常有效，尤其是当矩阵规模较大时。

具体例子：

假设有一个 3 * 3 的正定对称矩阵 (A) 如下：

$$A=\left(\begin{array}{ccc}4& 2& 1\\ 2& 5& 1\\ 1& 1& 2\end{array}\right)$$

我们来逐步进行Cholesky分解：

步骤 1: $$初始化下三角矩阵K，并设置K_{11}=\sqrt{A_{11}}。$$

$$K=\left(\begin{array}{ccc}\sqrt{4}& 0& 0\\ 0& 0& 0\\ 0& 0& 0\end{array}\right)=\left(\begin{array}{ccc}2& 0& 0\\ 0& 0& 0\\ 0& 0& 0\end{array}\right)$$

步骤 2: 用 (K) 的第一列计算 (A) 的第二行和第三行的第一项，然后解出 (K) 的第二个对角元素：

$$K_{22}=\sqrt{A_{22}-K_{21}^2}=\sqrt{5-2^2}=\sqrt{1}=1$$

现在 (K) 变为：
$$K=\left(\begin{array}{ccc}2& 0& 0\\ 0& 1& 0\\ 0& 0& 0\end{array}\right)$$

$$接下来计算K_{21}和K_{31}：$$

$$K_{21}=\frac{A_{12}}{K_{11}}=\frac{2}{2}=1,K_{31}=\frac{A_{13}}{K_{11}}=\frac{1}{2}$$

更新 (K)：

$$K=\left(\begin{array}{ccc}2& 0& 0\\ 1& 1& 0\\ \frac{1}{2}& 0& 0\end{array}\right)$$

步骤 3: 使用 (K) 的前两列计算 (A) 的剩余元素，并解出 (L) 的最后一个对角元素和非对角元素：

$$K_{33}=\sqrt{A_{33}-K_{31}^2-K_{32}^2}=\sqrt{2-{\left(\frac{1}{2}\right)}^2-0}=\sqrt{\frac{7}{4}}=\frac{\sqrt{7}}{2}$$

$$同时计算K_{32}：$$

$$K_{32}=\frac{A_{23}-K_{21}{K}_{31}}{L_{22}}=\frac{1-1\ast \frac{1}{2}}{1}=\frac{1}{2}$$

最终的 (K) 为：

$$K=\left(\begin{array}{ccc}2& 0& 0\\ 1& 1& 0\\ \frac{1}{2}& \frac{1}{2}& \frac{\sqrt{7}}{2}\end{array}\right)$$

$$现在，如果我们将K与其转置K^T相乘，应得到原始矩阵A：$$

$$K{K}^T=\left(\begin{array}{ccc}2& 0& 0\\ 1& 1& 0\\ \frac{1}{2}& \frac{1}{2}& \frac{\sqrt{7}}{2}\end{array}\right)\left(\begin{array}{ccc}2& 1& \frac{1}{2}\\ 0& 1& \frac{1}{2}\\ 0& 0& \frac{\sqrt{7}}{2}\end{array}\right)=A$$

通过上述步骤，我们完成了正定对称矩阵 (A) 的Cholesky分解。