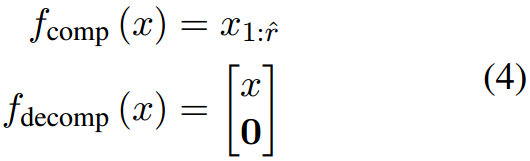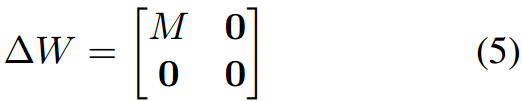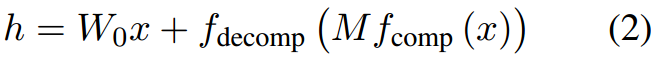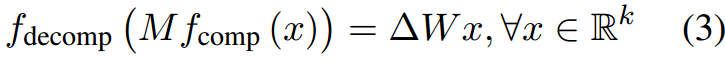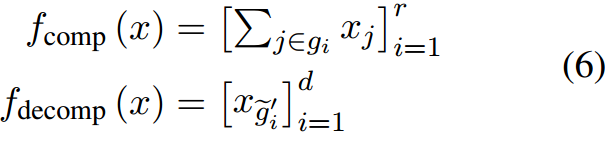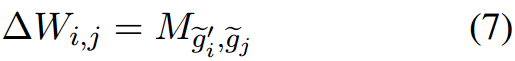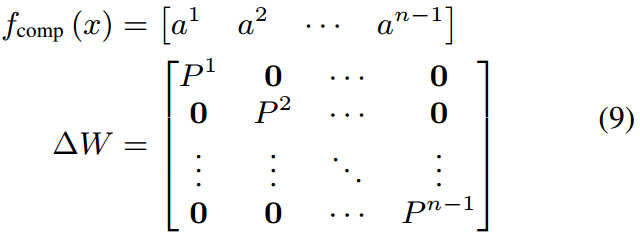文章汇总
LoRA的问题
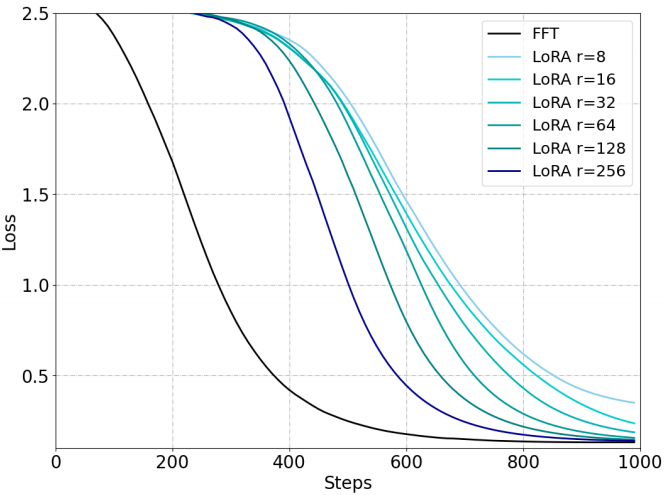
与FFT相比,低秩更新难以记忆新知识。虽然不断提高LoRA的秩可以缓解这一问题,但差距仍然存在。
动机
尽可能地利用相同的可训练参数来获得更高的
Δ
W
\Delta W
ΔW秩。
考虑到预训练权值
W
0
∈
R
d
×
k
W_0\in R^{d\times k}
W0∈Rd×k ,LoRA使用两个低秩矩阵
A
A
A和
B
B
B,它们有
(
d
+
k
)
r
(d+k)r
(d+k)r个总可训练参数。在相同的可训练参数下,一个方阵
M
∈
R
r
^
×
r
^
M \in R^{\hat r \times \hat r}
M∈Rr^×r^,其中
r
^
=
⌊
(
d
+
k
)
r
⌋
\hat r=\lfloor\sqrt{(d+k)r}\rfloor
r^=⌊(d+k)r⌋,由于
r
≪
m
i
n
(
d
,
k
)
r \ll min(d,k)
r≪min(d,k),因此这种做法可以获得最高秩。
方法
该图b秩的大小计算方式为
r
^
=
⌊
(
d
+
k
)
r
⌋
\hat r=\lfloor\sqrt{(d+k)r}\rfloor
r^=⌊(d+k)r⌋,其中
r
r
r是LoRA中使用的秩,这样的目的是跟LoRA保持同样的训练参数大小。
剩下一个头疼的问题是:如何将MoRA这个思路改动放在LoRA的代码里。
这里有一些符号定义,目的就是跟LoRA结合在一起
h
=
W
0
x
+
Δ
W
=
W
0
x
+
f
d
e
c
o
m
p
(
M
f
c
o
m
p
(
x
)
)
h=W_0x+\Delta W=W_0x+f_{decomp}(Mf_{comp}(x))
h=W0x+ΔW=W0x+fdecomp(Mfcomp(x))
式中
f
c
o
m
p
:
R
k
→
R
r
^
f_{comp}:R^k\rightarrow R^{\hat r}
fcomp:Rk→Rr^表示将
x
x
x的输入维数从
k
k
k减小到
r
^
\hat r
r^,
f
d
e
c
o
m
p
:
R
r
^
→
R
d
f_{decomp}: R^{\hat r} \rightarrow R^d
fdecomp:Rr^→Rd表示将输出维数从
r
^
\hat r
r^增大到
d
d
d。
式中
Δ
W
=
f
d
e
c
o
m
p
‾
(
f
c
o
m
p
‾
(
M
)
)
\Delta W=f_{\overline{decomp}}(f_{\overline{comp}}(M))
ΔW=fdecomp(fcomp(M)),
f
c
o
m
p
‾
:
R
r
^
×
r
^
→
R
r
^
×
k
f_{\overline{comp}}:R^{\hat r \times \hat r}\rightarrow R^{\hat r \times k}
fcomp:Rr^×r^→Rr^×k和
f
d
e
c
o
m
p
‾
:
R
r
^
×
k
→
R
d
×
k
f_{\overline{decomp}}:R^{\hat r \times k}\rightarrow R^{d\times k}
fdecomp:Rr^×k→Rd×k。
对于
f
c
o
m
p
f_{comp}
fcomp和
f
d
e
c
o
m
p
f_{decomp}
fdecomp的设计,作者探索了几种实现这些功能的方法。这里列举简单了两种。
Fcomp和Fdecomp的设计
截断维度
对应的
Δ
W
\Delta W
ΔW为:
图解如下
f
c
o
m
p
f_{comp}
fcomp只取
x
x
x的前
r
^
\hat r
r^行和前
r
^
\hat r
r^列,
f
d
e
c
o
m
p
f_{decomp}
fdecomp用0矩阵来增大维度到
d
d
d。明显这种方法在压缩过程中会导致大量的信息丢失,
共享M的行和列
f
c
o
m
p
:
R
k
→
R
n
×
r
^
,
f
d
e
c
o
m
p
:
R
n
×
r
^
→
R
d
f_{comp}:R^k\rightarrow R^{n\times \hat r},f_{decomp}: R^{n\times \hat r} \rightarrow R^d
fcomp:Rk→Rn×r^,fdecomp:Rn×r^→Rd。对应的
f
c
o
m
p
,
f
d
e
c
o
m
p
,
Δ
W
f_{comp},f_{decomp},\Delta W
fcomp,fdecomp,ΔW为:
例子,当
r
=
128
r=128
r=128,
Δ
W
∈
R
d
×
k
=
R
4096
×
4096
\Delta W \in R^{d\times k}=R^{4096\times 4096}
ΔW∈Rd×k=R4096×4096时,
r
^
=
⌊
(
d
+
k
)
r
⌋
=
⌊
(
4096
+
4096
)
×
128
⌋
=
1024
,
M
∈
R
r
^
×
r
^
=
R
1024
×
1024
\hat r=\lfloor\sqrt{(d+k)r}\rfloor=\lfloor\sqrt{(4096+4096)\times 128}\rfloor=1024,M \in R^{\hat r\times \hat r}=R^{1024\times 1024}
r^=⌊(d+k)r⌋=⌊(4096+4096)×128⌋=1024,M∈Rr^×r^=R1024×1024。
图解如下
摘要
低秩自适应(Low-rank adaptation, LoRA)是一种针对大型语言模型的参数有效微调(PEFT)方法。在本文中,我们分析了在LoRA中实现的低秩更新的影响。我们的研究结果表明,低等级的更新机制可能会限制LLM有效学习和记忆新知识的能力。受此启发,我们提出了一种新的方法,称为MoRA,该方法采用方阵来实现高秩更新,同时保持相同数量的可训练参数。为了实现这一目标,我们引入了相应的非参数算子来减少方阵的输入维数和增加输出维数。此外,这些操作确保了权重可以合并回LLM,这使得我们的方法可以像LoRA一样部署。我们在五个任务中对我们的方法进行了全面的评估:指令调整、数学推理、持续预训练、记忆和预训练。我们的方法在内存密集型任务上优于LoRA,在其他任务上也达到了相当的性能。我们的代码可以在https://github.com/kongds/MoRA上找到。
1.介绍
随着语言模型规模的增加,参数有效微调(PEFT) (Houlsby等人,2019)已经成为一种流行的技术,可以使这些模型适应特定的下游任务。与更新所有模型参数的完全微调(FFT)相比,PEFT只修改了一小部分参数。例如,在某些任务中,它可以通过更新不到1%的参数来实现与FFT相似的性能(Hu et al, 2021),这大大降低了优化器的内存需求,并促进了微调模型的存储和部署。在现有的PEFT方法中,Low-Rank Adaptation (LoRA) (Hu et al ., 2021)在LLM尤为突出。LoRA通过通过低秩矩阵更新参数,提高了其他PEFT方法的性能,如提示调优(Lester等人,2021)或适配器(Houlsby等人,2019)。这些矩阵可以合并到原始模型参数中,从而避免了推理过程中额外的计算成本。有许多方法旨在改进LLM的LoRA。然而,大多数方法主要是基于GLUE验证其效率(Wang et al ., 2018),要么通过实现更好的性能,要么通过需要更少的可训练参数。最新方法(Liu et, 2024;Meng等,2024;Zhu等人,2024)利用指令调优任务如Alpaca (Wang等人,2024)或推理任务如GSM8K (Cobbe等人,2021)来更好地评估它们在LLM上的性能。然而,评估中使用的不同设置和数据集使对其进展的理解复杂化。
在本文中,我们在相同设置下对不同任务的LoRA进行了全面评估,包括指令调优、数学推理和持续预训练,,包括指令调整、数学推理和持续的预训练。我们发现,类似lora的方法在这些任务中表现出类似的性能,它们在指令调优方面的表现与FFT相当,但在数学推理和持续预训练方面存在不足。在这些任务中,指令调优主要侧重于与格式的交互,而不是获取知识和能力,这些知识和能力几乎完全是在预训练期间学习的(Zhou et al, 2024)。我们观察到,LoRA很容易适应指令调优中的响应格式,但在其他需要通过微调增强知识和能力的任务中却遇到困难。
对于LoRA观察到的这种限制,一个合理的解释可能是它依赖于低秩更新(Lialin et al, 2023)。低秩更新矩阵
Δ
W
\Delta W
ΔW难以估计FFT中的全秩更新,特别是在需要记忆特定领域知识的持续预训练等内存密集型任务中。由于
Δ
W
\Delta W
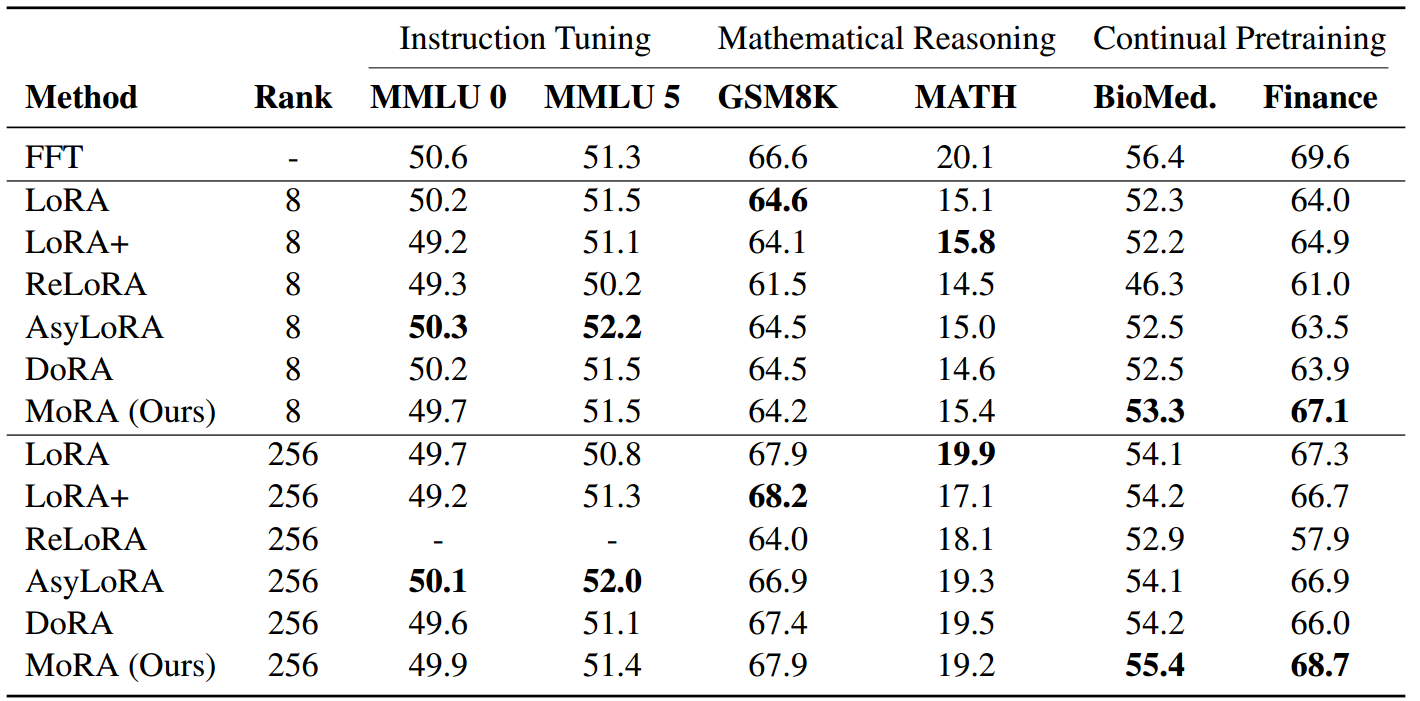
ΔW的秩明显小于全秩,这一限制限制了通过微调存储新信息的能力。此外,当前的LoRA变体不能改变低秩更新的固有特征。为了验证这一点,我们使用伪数据进行了一个记忆任务,以评估LoRA在记忆新知识方面的性能。我们发现LoRA的表现明显不如FFT,即使是256这样的大秩也是如此。
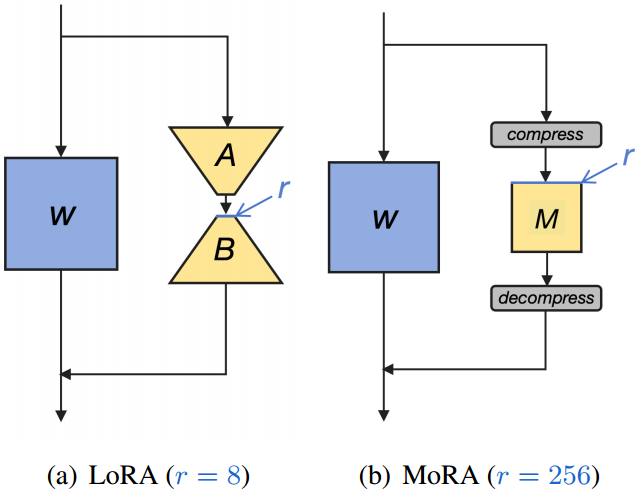
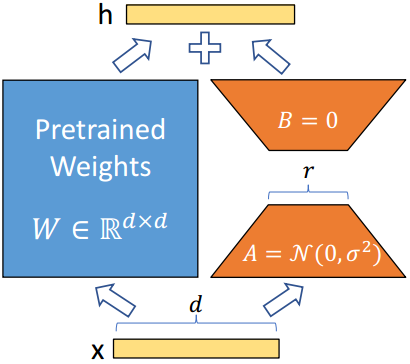
图1:在相同数量的可训练参数下,与LoRA相比,我们的方法的概述。
W
W
W为模型的冷冻重量。
A
A
A和
B
B
B是LoRA中可训练的低秩矩阵。
M
M
M是我们方法中的可训练矩阵。灰色部分是用于减少输入维数和增加输出维数的非参数算子。
r
r
r表示两种方法中的秩。
鉴于这些观察结果,我们引入了一种称为MoRA的方法,该方法采用与低秩矩阵相反的方阵,旨在最大化
Δ
W
\Delta W
ΔW中的秩,同时保持相同数量的可训练参数。例如,当使用8秩,隐藏大小为4096时,LoRA使用两个低秩矩阵
A
∈
R
4096
×
8
A \in R^{4096\times 8}
A∈R4096×8和
B
∈
R
8
×
4096
B \in R^{8\times 4096 }
B∈R8×4096,
r
a
n
k
(
Δ
W
)
≤
8
rank( \Delta W)\le 8
rank(ΔW)≤8。在参数数相同的情况下,我们的方法使用一个方阵
M
∈
R
256
×
256
M \in R^{256\times 256}
M∈R256×256,秩
r
a
n
k
(
Δ
W
)
≤
8
rank( \Delta W)\le 8
rank(ΔW)≤8,如图1所示。值得注意的是,我们的方法显示出比具有大秩的LoRA更大的容量。为了减小
M
M
M的输入维数,增大
M
M
M**的输出维数,我们开发了相应的非参数算子。**此外,这些算子和
M
M
M可以用
Δ
W
\Delta W
ΔW代替,确保我们的方法可以像LoRA一样合并回LLM。
我们的贡献如下:
1.我们引入了一种新的方法MoRA,它在保持相同数量的可训练参数的情况下,在LoRA中使用方阵代替低秩矩阵来实现高秩更新。
2.我们讨论了四种MoRA的非参数算子,以降低方阵的输入维数和增加输出维数,同时保证权值可以合并回LLM。
3.我们通过五个任务评估MoRA:记忆、指令调整、数学推理、持续预训练和预训练。我们的方法在内存密集型任务上优于LoRA,在其他任务上也达到了相当的性能,这证明了高秩更新的有效性。
2.相关工作
2.1 LoRA
与其他方法相比,LoRA具有广泛的适用性和鲁棒性,是最流行的用于LLM微调的PEFT方法之一。为了近似FFT中更新后的权值
Δ
W
\Delta W
ΔW, LoRA采用两个低秩矩阵进行分解。通过调整这两个矩阵的秩,LoRA可以相应地修改可训练参数。得益于此,LoRA可以在微调后合并这些矩阵,而不会产生与FFT相比的推理延迟。有许多方法可以进一步改进LoRA,特别是在LLM中的应用。DoRA(Liu et al ., 2024)进一步将原始权重分解为幅度分量和方向分量,并使用LoRA对方向分量进行更新。LoRA+(Hayou et al ., 2024)对两个低秩矩阵采用不同的学习率来提高学习效率。ReLoRA(Lialin et al, 2023)在训练期间将LoRA集成到LLM中,以提高最终
Δ
W
\Delta W
ΔW的秩。
2.2 LLMs微调
尽管LLM在上下文学习方面的表现令人印象深刻,但某些场景仍然需要微调,大致可以分为三种类型。第一种类型,指令调优,旨在更好地将LLM与最终任务和用户偏好结合起来,而不会显着增强LLM的知识和能力(Zhou et al, 2024)。这种方法简化了处理不同的任务,理解复杂的指令的过程。第二种类型涉及复杂的推理任务,如数学问题解决(Collins et al, 2023;Imani et al ., 2023;Yu et al ., 2023),其中一般指令调优在处理复杂的、象征性的、多步骤的推理任务时往往不足。为了提高LLM的推理能力,大多数研究都集中在创建相应的训练数据集上,要么利用更大的教师模型,如GPT-4 (Fu et al ., 2023),要么沿着推理路径改写问题(Yu et al ., 2023)。第三种是持续预训练(Cheng et al ., 2023;Chen et al ., 2023;Han等,2023;Liu et al ., 2023),旨在增强LLM的特定领域能力。与指令调优不同,它需要微调以增加相应的特定领域知识和功能。
然而,LoRA的大多数变体(Kopiczko等人,2023;Lialin等,2023;Dettmers等,2024;Zhu等人,2024)主要使用GLUE中的指令调优或文本分类任务(Wang等人,2018)来验证它们在LLM上的有效性。鉴于与其他类型相比,指令调优需要的微调能力最少,因此它可能无法准确反映LoRA变体的有效性。为了更好地评估他们的方法,最近的研究(Meng et al ., 2024;Liu et al ., 2024;Shi et al ., 2024;Renduchintala等人,2023)使用推理任务来测试他们的方法。但所使用的训练集往往太小,LLM无法有效地学习推理。例如,一些方法(Meng et al, 2024;Renduchintala等人,2023)使用仅7.5K训练样本的GSM8K (Cobbe等人,2021)。与395K训练样本的SOTA方法(Yu et al ., 2023)相比,这个小的训练集在推理上的表现更差,很难评估这些方法的有效性。
3.分析低秩更新的影响
LoRA的关键思想(Hu et al, 2021)涉及使用低秩更新来估计FFT中的全秩更新。形式上,给定一个预训练的参数矩阵
W
0
∈
R
d
×
k
W_0 \in R^{d\times k}
W0∈Rd×k, LoRA采用两个低秩矩阵计算权值更新
Δ
W
\Delta W
ΔW:
h
=
W
0
x
+
△
W
x
=
W
0
x
+
B
A
x
,
B
∈
R
d
×
r
,
A
∈
R
r
×
k
,
r
≪
m
i
n
(
d
,
k
)
h=W_0x+\triangle Wx=W_0x+BAx,B\in \mathbb{R}^{d\times r},A\in \mathbb{R}^{r\times k},r \ll min(d,k)
h=W0x+△Wx=W0x+BAx,B∈Rd×r,A∈Rr×k,r≪min(d,k)
其中,
A
∈
R
r
×
k
,
B
∈
R
d
×
r
A \in R^{r\times k},B\in R^{d \times r}
A∈Rr×k,B∈Rd×r表示LoRA中的低秩矩阵。确保
Δ
W
=
0
\Delta W=0
ΔW=0在训练开始时,LoRA用高斯分布初始化
A
A
A,用零初始化
B
B
B。由于
Δ
W
\Delta W
ΔW分解为
B
A
BA
BA,
r
a
n
k
(
Δ
W
)
≤
r
rank( \Delta W)\le r
rank(ΔW)≤r。与FFT中的全秩更新相比,LoRA中的权重更新的秩明显较低,
r
≪
m
i
n
(
d
,
k
)
r \ll min(d,k)
r≪min(d,k)。LoRA的低秩更新在文本分类或指令调优等任务中表现出与全秩更新相当的性能(Liu et al ., 2024;Meng et al, 2024)。然而,对于复杂推理或持续预训练等任务,LoRA往往表现出更差的性能(Liu et al ., 2023)。
基于这些观察,我们提出了一个假设,即低秩更新容易利用LLM原有的知识和能力来解决任务,但很难处理需要提高LLM知识和能力的任务。
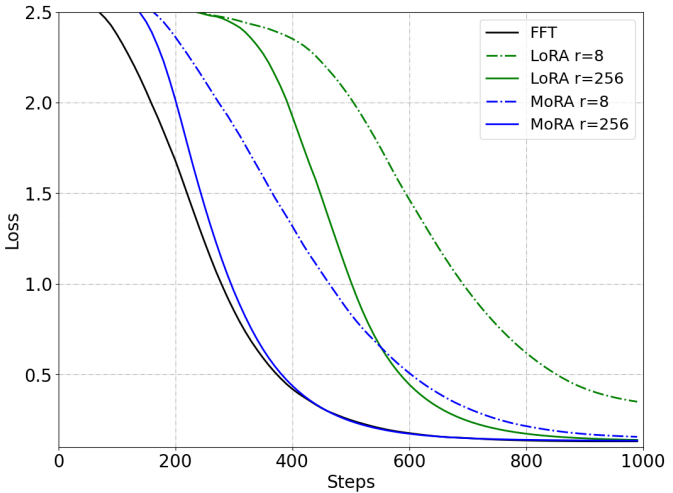
为了证实这一假设,我们研究了LoRA和FFT在通过微调记忆新知识方面的差异。为了避免利用LLM的原始知识,我们随机生成10K对通用唯一标识符(uuid),每对包含两个具有32个十六进制值的uuid。该任务要求LLM根据输入的UUID生成相应的UUID。例如,给定一个UUID,如“205f3777-52b6-4270-9f67-c5125867d358”,模型应该基于10K对训练对生成相应的UUID。这个任务也可以被看作是一个问答任务,而完成它所必需的知识完全来自训练数据集,而不是LLM本身。
对于训练设置,我们使用LLaMA-27B为基础模型,每批使用1000对,进行100次epoch。对于LoRA,我们将低秩矩阵应用于所有线性层,并从{1e-4,2e-4,3e-4}搜索学习率以提高性能。我们使用不同秩
r
∈
{
8
,
16
,
32
,
64
,
128
,
256
}
r \in \{8,16,32,64,128,256\}
r∈{8,16,32,64,128,256}对LoRA进行实验。对于FFT,我们直接使用3e-5的学习率。
图2:使用FFT和LoRA进行微调来记忆UUID对的性能。
根据图2,我们观察到与FFT相比,低秩更新难以记忆新知识。虽然不断提高LoRA的秩可以缓解这一问题,但差距仍然存在。与内存任务相比,我们还评估了LoRA和FFT在指令调优方面的性能差距,这只是引入了新的知识。与之前的结果相似(Meng et al ., 2024;Zhu et al ., 2024),我们也发现LoRA与表1中
r
=
8
r=8
r=8的小秩FFT的性能相匹配。这表明LoRA可以通过像FFT一样的微调轻松地利用LLM的原始知识。
4.方法
基于以上分析,我们提出了一种新的方法来缓解低秩更新的负面影响。我们的方法的主要思想是尽可能地利用相同的可训练参数来获得更高的
Δ
W
\Delta W
ΔW秩。考虑到预训练权值
W
0
∈
R
d
×
k
W_0\in R^{d\times k}
W0∈Rd×k ,LoRA使用两个低秩矩阵
A
A
A和
B
B
B,它们有
(
d
+
k
)
r
(d+k)r
(d+k)r个总可训练参数。在相同的可训练参数下,一个方阵
M
∈
R
r
^
×
r
^
M \in R^{\hat r \times \hat r}
M∈Rr^×r^,其中
r
^
=
⌊
(
d
+
k
)
r
⌋
\hat r=\lfloor\sqrt{(d+k)r}\rfloor
r^=⌊(d+k)r⌋,由于
r
≪
m
i
n
(
d
,
k
)
r \ll min(d,k)
r≪min(d,k),因此可以获得最高秩。
为了实现这一点,我们需要减少
M
M
M的输入维数,增加
M
M
M的输出维数。
式中,
f
c
o
m
p
:
R
k
→
R
r
^
f_{comp}:R^k\rightarrow R^{\hat r}
fcomp:Rk→Rr^表示将
x
x
x的输入维数从
k
k
k减小到
r
^
\hat r
r^,
f
d
e
c
o
m
p
:
R
r
^
→
R
d
f_{decomp}: R^{\hat r} \rightarrow R^d
fdecomp:Rr^→Rd表示将输出维数从
r
^
\hat r
r^增大到
d
d
d。此外,这两个函数应该是非参数化的运算符,并期望在相应维度的线性时间内执行。它们还应具有相应的功能,
f
c
o
m
p
‾
:
R
r
^
×
r
^
→
R
r
^
×
k
f_{\overline{comp}}:R^{\hat r \times \hat r}\rightarrow R^{\hat r \times k}
fcomp:Rr^×r^→Rr^×k和
f
d
e
c
o
m
p
‾
:
R
r
^
×
k
→
R
d
×
k
f_{\overline{decomp}}:R^{\hat r \times k}\rightarrow R^{d\times k}
fdecomp:Rr^×k→Rd×k,将
M
M
M转化为
Δ
W
\Delta W
ΔW。对于任意
x
x
x,下列条件都成立:
式中
Δ
W
=
f
d
e
c
o
m
p
‾
(
f
c
o
m
p
‾
(
M
)
)
\Delta W=f_{\overline{decomp}}(f_{\overline{comp}}(M))
ΔW=fdecomp(fcomp(M))。若Eq. 3成立,则
M
M
M可根据
f
c
o
m
p
f_{comp}
fcomp和
f
d
e
c
o
m
p
f_{decomp}
fdecomp无损展开为
Δ
W
\Delta W
ΔW。这允许我们的方法像LoRA一样合并回LLM。
对于
f
c
o
m
p
f_{comp}
fcomp和
f
d
e
c
o
m
p
f_{decomp}
fdecomp的设计,我们探索了几种实现这些功能的方法。一种简单的方法是截断维度,然后将其添加到相应的维度中。在形式上,这可以表示为:
对应的
Δ
W
\Delta W
ΔW为:
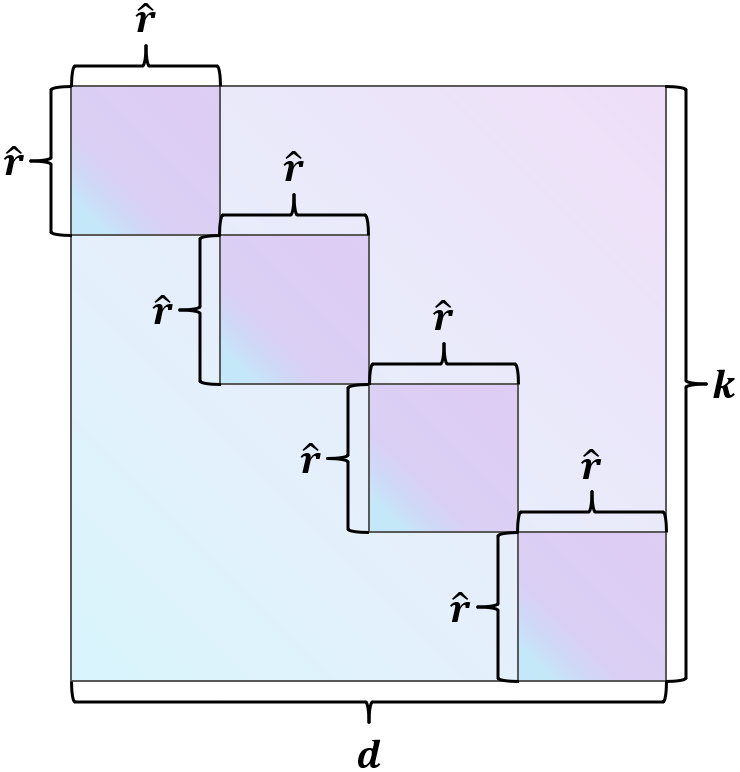
然而,这种方法在压缩过程中会导致大量的信息丢失,并且在解压缩过程中只通过附加零向量来修改输出的一部分。为了改进它,我们可以共享M的行和列,以实现更有效的压缩和解压缩。在形式上,这可以表示为:
这里,
g
g
g和
g
′
g'
g′分别表示
M
M
M中共享同一行和同一列的预定义组。
j
∈
g
i
j \in g_i
j∈gi表示第
j
j
j维属于
g
g
g中的第
i
i
i个组。
g
~
i
′
\tilde{g}'_i
g~i′是
g
i
′
{g}'_i
gi′的反转,表示与
g
′
g'
g′中的第
g
~
i
′
\tilde{g}'_i
g~i′个组相关的第
i
i
i维。对应的
Δ
W
\Delta W
ΔW为:
对于较大的秩(如
r
=
128
r=128
r=128或
r
=
256
r=256
r=256),共享行和列可能是有效的,因为
Δ
W
\Delta W
ΔW中只有少数行或列共享公共行或列。例如,考虑
r
=
128
r=128
r=128时,
Δ
W
∈
R
4096
×
4096
\Delta W \in R^{4096\times 4096}
ΔW∈R4096×4096,其中,
r
^
=
1024
,
M
∈
R
1024
×
1024
\hat r=1024,M \in R^{1024\times 1024}
r^=1024,M∈R1024×1024。在这种情况下,只有4行或4列共享同一行或列。相反,对于较小的秩,如
r
=
8
r=8
r=8,其中
r
^
=
256
\hat r=256
r^=256,则平均需要16行或列在一组中共享
M
M
M中的同一行或列,这可能导致效率低下,因为在Eq. 6中压缩过程中存在显着的信息丢失。
为了提高较小秩的性能,我们重塑
x
x
x而不是直接压缩它,以保留输入信息。在这种情况下,
f
c
o
m
p
:
R
k
→
R
n
×
r
^
,
f
d
e
c
o
m
p
:
R
n
×
r
^
→
R
d
f_{comp}:R^k\rightarrow R^{n\times \hat r},f_{decomp}: R^{n\times \hat r} \rightarrow R^d
fcomp:Rk→Rn×r^,fdecomp:Rn×r^→Rd。对应的
f
c
o
m
p
,
f
d
e
c
o
m
p
,
Δ
W
f_{comp},f_{decomp},\Delta W
fcomp,fdecomp,ΔW为:
其中
c
o
n
c
a
t
(
x
)
concat(x)
concat(x)指的是将
x
x
x的行连接成一个向量。为了简单起见,我们省略了上述函数中的填充和截断操作符,并将重点放在
d
=
k
d = k
d=k的情况下。与共享列和行相比,该方法通过将
x
x
x重塑为
R
n
×
r
^
R^{n\times \hat r}
Rn×r^而不是
R
r
^
R^{ \hat r}
Rr^来增加额外的计算开销。然而,考虑到
M
M
M的大小明显小于
W
0
W_0
W0,这个额外的计算对于像8这样的秩来说是非常小的。例如,当对
r
a
n
k
rank
rank为8
(
r
^
=
256
)
(\hat r = 256)
(r^=256)的7B模型进行微调时,该方法仅比以前的方法慢1.03倍。
受RoPE (Su等人,2024)的启发,我们可以进一步改进该方法,通过将旋转算子合并到
f
c
o
m
p
f_{comp}
fcomp中来增强
M
M
M的表达性,使其能够通过旋转来区分不同的
x
i
r
^
:
(
i
+
1
)
r
^
x_{i\hat r:(i+1)\hat r}
xir^:(i+1)r^。我们可以将Eq. 8修改为:
其中,
a
i
a^i
ai和
P
i
P^i
Pi分别表示旋转后
x
i
r
^
:
(
i
+
1
)
r
^
x_{i\hat r:(i+1)\hat r}
xir^:(i+1)r^和
M
M
M的对应值。在RoPE之后,我们使用
r
^
×
r
^
\hat r\times \hat r
r^×r^块对角矩阵来实现旋转。然而,我们的方法使用旋转信息使M能够区分
x
i
r
^
:
(
i
+
1
)
r
^
x_{i\hat r:(i+1)\hat r}
xir^:(i+1)r^,而不是RoPE中的标记位置。我们可以定义
a
i
a^i
ai和
P
i
P^i
Pi如下:
其中
θ
j
=
1000
0
−
2
(
j
−
1
)
/
r
^
,
R
θ
j
,
i
∈
R
2
×
2
\theta_j=10000^{-2(j-1)/\hat r},R_{\theta_j,i}\in R^{2\times 2}
θj=10000−2(j−1)/r^,Rθj,i∈R2×2为旋转矩阵:
5.实验
参考资料
论文下载
https://arxiv.org/abs/2405.12130
代码地址(286 stars)
https://github.com/kongds/MoRA