忆如完整项目/代码详见github：https://github.com/yiru1225（转载标明出处 勿白嫖 star for projects thanks）

目录

系列文章目录

一、PCA的概念与原理

1.PCA简介

2.PCA算法模型

二、PCA运用于人脸识别

1.预处理

1.1 数据导入与处理

1.2 数据集求均值与数据中心化

1.3 求协方差矩阵、特征值与特征向量并排序

2.人脸重构

3.人脸识别

4.人脸图像降维与可视化

5.其他

5.1 内部函数定义

5.2 数据集及资源

总结

系列文章目录

本系列博客重点在机器学习的概念原理与代码实践，不包含繁琐的数学推导（有问题欢迎在评论区讨论指出，或直接私信联系我）。

代码可以全抄    大家搞懂原理与流程去复现才是有意义的！！！
第一章 PCA与人脸识别

梗概

本篇博客主要介绍PCA（主成分分析）算法并将PCA用于人脸的重构、识别、图像降维可视化（内附数据集与matlab代码）

一、PCA的概念与原理

1.PCA简介

PCA（主成分分析）为主流的一种线性降维算法。以”最小重构误差“为目标导向，通过降维（投影），用数据中相对重要（最主要）的信息表达（代替）原数据，从而达到降维的目的。

2.PCA算法模型

经典的PCA解决问题可划分为以下步骤

① 数据的导入与处理（eg.人脸识别中需要将每一张人脸拉成一列或一行）

② 计算数据均值并对数据中心化

③ 计算协方差矩阵（散度矩阵）

④ 分解协方差矩阵得到按特征值从大到小排序的特征向量（也可用SVD分解）

⑤ 取出前k个特征向量作为投影，使原数据降维到对应投影方向，实现由原本n维数据降到k维

二、PCA运用于人脸识别

1.预处理

Tips：预处理包括数据导入处理、求均值去心化、分解协方差矩阵得到特征向量（特征脸）

1.1 数据导入与处理

利用imread批量导入人脸数据库，或直接load相应mat文件，并在导入时不断将人脸拉成一个个列向量组成reshaped_faces，本实验取出每个人的前30%作为测试数据，后70%作为训练数据。

clear;
% 1.人脸数据集的导入与数据处理（400张图，一共40人，一人10张）
%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%
reshaped_faces=[];
for i=1:40    
    for j=1:10       
        if(i<10)
           a=imread(strcat('C:\AR_Gray_50by40\AR00',num2str(i),'-',num2str(j),'.tif'));     
        else
            a=imread(strcat('C:\AR_Gray_50by40\AR0',num2str(i),'-',num2str(j),'.tif'));  
        end          
        b = reshape(a,2000,1); %将每一张人脸拉成列向量
        b=double(b); %utf-8转换为double类型，避免人脸展示时全灰的影响       
        reshaped_faces=[reshaped_faces, b];  
    end
end

% 取出前30%作为测试数据，剩下70%作为训练数据
test_data_index = [];
train_data_index = [];
for i=0:39
    test_data_index = [test_data_index 10*i+1:10*i+3];
    train_data_index = [train_data_index 10*i+4:10*(i+1)];
end

train_data = reshaped_faces(:,train_data_index);
test_data = reshaped_faces(:, test_data_index);

1.2 数据集求均值与数据中心化

利用mean函数对训练集求平均值，得出平均脸（如图1），将训练集中所有数据减去平均脸，实现中心化（中心化后某些人脸如图2，相对原图灰度值更低）。

% 2.图像求均值，中心化
%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%

% 求平均脸
mean_face = mean(train_data,2);
%waitfor(show_face(mean_face)); %平均脸展示，测试用

% 中心化
centered_face = (train_data - mean_face);
%用于展示中心化后某些训练图片 测试用
%waitfor(show_faces(centered_face));

图1 AR数据集中的平均脸

图2 中心化后的部分人脸 

1.3 求协方差矩阵、特征值与特征向量并排序

根据数学推导，协方差矩阵可由cov_matrix = centered_face（中心化人脸数据集） * centered_face'求得，再利用eig函数基于特征值对协方差矩阵进行分解（或使用SVD），并用sort函数将特征向量按从大到小排序好，得到所有特征脸（部分特征脸如图3）。

% 3.求协方差矩阵、特征值与特征向量并排序
%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%

% 协方差矩阵
cov_matrix = centered_face * centered_face';
[eigen_vectors, dianogol_matrix] = eig(cov_matrix);

% 从对角矩阵获取特征值
eigen_values = diag(dianogol_matrix);

% 对特征值按索引进行从大到小排序
[sorted_eigen_values, index] = sort(eigen_values, 'descend'); 

% 获取排序后的征值对应的特征向量
sorted_eigen_vectors = eigen_vectors(:, index);

% 特征脸(所有）
all_eigen_faces = sorted_eigen_vectors;

%用于展示某些特征脸 测试用
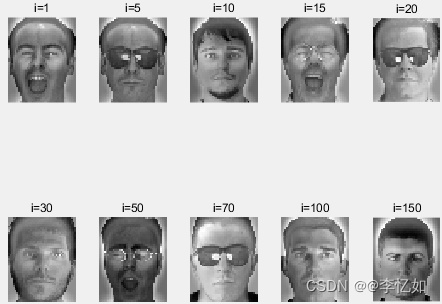
waitfor(show_faces(all_eigen_faces));

图3 部分特征脸（eigenface）

Tips：一个特征脸即一个特征向量，数据集中所有人脸都是由某些特征脸组合得到，故利用特征向量（特征脸）是后续实现人脸重构、识别、降维可视化的关键。

2.人脸重构

重构的意义：检测特征脸对人脸的还原度与维数的关系（数据降到多少维才能较好还原原始数据）

从已中心化的centered_faces中取出某人脸，用20,40,60,80,...,160个投影（前n个特征向量）按公式rebuild_face = eigen_faces * (eigen_faces' * single_face) + mean_face来重构此人脸，并观察在不同数量的投影下的还原度，重构效果如图4。

%%人脸重构

% 取出第一个人的人脸，用于重构
single_face = centered_face(:,1);

index = 1;
for dimensionality=20:20:160

    % 取出相应数量特征脸（前n大的特征向量，用于重构人脸）
    eigen_faces = all_eigen_faces(:,1:dimensionality);

    % 重建人脸并显示
        rebuild_face = eigen_faces * (eigen_faces' * single_face) + mean_face;
        subplot(2, 4, index); %两行四列
        index = index + 1;
        fig = show_face(rebuild_face);
        title(sprintf("dimensionality=%d", dimensionality));    
        if (dimensionality == 160)
            waitfor(fig);
        end
end

图4 不同维度下人脸还原（重构）效果 

3.人脸识别

Tips：本实验中有两个变量，k从1~6取值，维度从10~160，探究k值及维度对识别率的共同影响

分别对测试集、训练集进行降维，将人脸投影到10，20，30，…，160维空间中，计算未知人脸与所有已知人脸的距离（欧几里得距离），然后使用最近邻分类器KNN进行识别（共同影响如图5 只考虑维度影响如图6 横坐标为维度/10）

% 5.人脸识别
%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%

index = 1;       
Y = [];
% KNN
for k=1:6

    for i=10:10:160
    % 取出相应数量特征脸
   eigen_faces = all_eigen_faces(:,1:i);
    % 测试、训练数据降维
    projected_train_data = eigen_faces' * (train_data - mean_face);
    projected_test_data = eigen_faces' * (test_data - mean_face);
        % 用于保存最小的k个值的矩阵
        % 用于保存最小k个值对应的人标签的矩阵
        minimun_k_values = zeros(k,1);
        label_of_minimun_k_values = zeros(k,1);

        % 测试脸的数量
        test_face_number = size(projected_test_data, 2);

        % 识别正确数量
        correct_predict_number = 0;

        % 遍历每一个待测试人脸
        for each_test_face_index = 1:test_face_number

            each_test_face = projected_test_data(:,each_test_face_index);

            % 先把k个值填满，避免在迭代中反复判断
            for each_train_face_index = 1:k
                minimun_k_values(each_train_face_index,1) = norm(each_test_face - projected_train_data(:,each_train_face_index));
                label_of_minimun_k_values(each_train_face_index,1) = floor((train_data_index(1,each_train_face_index) - 1) / 10) + 1;
            end

            % 找出k个值中最大值及其下标
            [max_value, index_of_max_value] = max(minimun_k_values);

            % 计算与剩余每一个已知人脸的距离
            for each_train_face_index = k+1:size(projected_train_data,2)

                % 计算距离
                distance = norm(each_test_face - projected_train_data(:,each_train_face_index));

                % 遇到更小的距离就更新距离和标签
                if (distance < max_value)
                    minimun_k_values(index_of_max_value,1) = distance;
                    label_of_minimun_k_values(index_of_max_value,1) = floor((train_data_index(1,each_train_face_index) - 1) / 10) + 1;
                    [max_value, index_of_max_value] = max(minimun_k_values);
                end
            end

            % 最终得到距离最小的k个值以及对应的标签
            % 取出出现次数最多的值，为预测的人脸标签
            predict_label = mode(label_of_minimun_k_values);
            real_label = floor((test_data_index(1,each_test_face_index) - 1) / 10)+1;

            if (predict_label == real_label)
                %fprintf("预测值：%d，实际值:%d，正确\n",predict_label,real_label);
                correct_predict_number = correct_predict_number + 1;
            else
                %fprintf("预测值：%d，实际值:%d，错误\n",predict_label,real_label);
            end
        end
        % 单次识别率
        correct_rate = correct_predict_number/test_face_number;

        Y = [Y correct_rate];

        fprintf("k=%d，i=%d，总测试样本：%d，正确数:%d，正确率：%1f\n", k, i,test_face_number,correct_predict_number,correct_rate);
    end
end
% 求不同k值不同维度下的人脸识别率及平均识别率
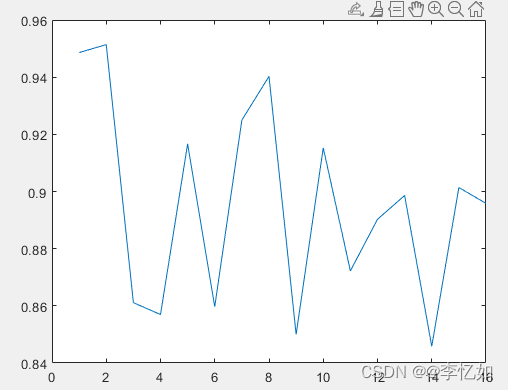
Y = reshape(Y,k,16);
waitfor(waterfall(Y));
avg_correct_rate=mean(Y);
waitfor(plot(avg_correct_rate));

 图5 不同k值与维度下PCA的人脸识别率

  图6 不同维度下PCA的人脸识别率（横坐标为维度/10）

4.人脸图像降维与可视化

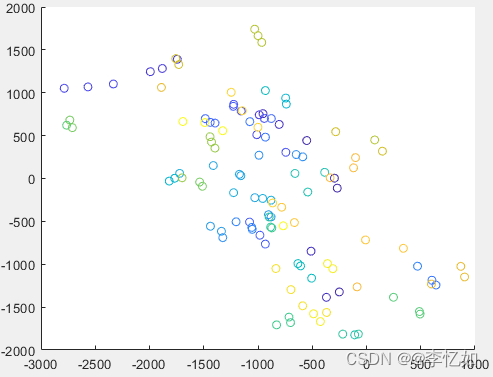
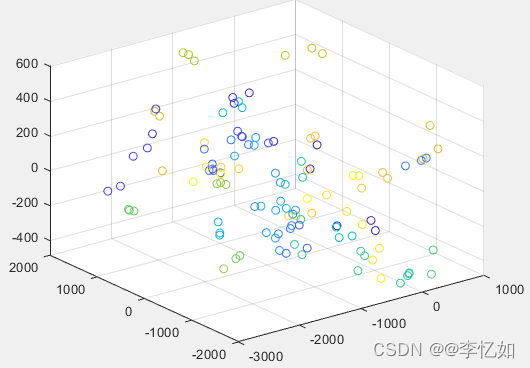
取出对应数量的特征脸（n维取n个），利用公式projected_test_data = eigen_faces' * (test_data - mean_face)对测试集或其他子集进行投影，投影后上色（同人同色）并使用scatter画图实现可视化（二维人脸分布如图7，三维人脸分布如图8）。

Tips：本实验以测试集的二三维可视化为例

% 6.人脸数据二三维可视化（可推广到不同数据集）
%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%

for i=[2 3]

    % 取出相应数量特征脸
    eigen_faces = all_eigen_faces(:,1:i);

    % 投影
    projected_test_data = eigen_faces' * (test_data - mean_face);

    color = [];
    for j=1:120
        color = [color floor((j-1)/4)*5];
    end

    % 显示
    if (i == 2)
        waitfor(scatter(projected_test_data(1, :), projected_test_data(2, :), [], color));
    else
        waitfor(scatter3(projected_test_data(1, :), projected_test_data(2, :), projected_test_data(3, :), [], color));
    end

end

图7 测试集降维至二维图像分布

 图8 测试集降维至三维图像分布

5.其他

5.1 内部函数定义

本实验中将人脸图像展示抽象为函数，函数定义如下：

%内用函数定义
%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%

% 输入向量，显示脸
function fig = show_face(vector)
    fig = imshow(mat2gray(reshape(vector, [50, 40])));
end

% 显示矩阵中某些脸
function fig = show_faces(eigen_vectors)
    count = 1;
    index_of_image_to_show = [1,5,10,15,20,30,50,70,100,150];
    for i=index_of_image_to_show
        subplot(2,5,count);
        fig = show_face(eigen_vectors(:, i));
        title(sprintf("i=%d", i));
        count = count + 1;
    end
end

5.2 数据集及资源

本实验以AR50_40数据集做展示，代码可适用多个数据集。

常用人脸数据集如下（不要白嫖哈哈哈）

链接：https://pan.baidu.com/s/12Le0mKEquGMgh5fhNagZGw 
提取码：yrnb

PCA完整代码：李忆如/忆如的机器学习 - Gitee.com

5.3 参考资料

1.赖志辉的课

2. PCA原理_PiggyGaGa的博客-CSDN博客_pca

3.基于 PCA 的人脸识别方法——特征脸法[2] - 知乎 (zhihu.com)

4.周志华《机器学习》

总结

PCA作为经典的线性降维算法，通过”最小重构误差“为目标导向对数据进行投影实现降维，如今仍然在机器学习许多领域（语言图像处理、数据可视化）有优异表现。但作为一种无监督学习方法（没有对训练样本做标注），在对数据完全无知的情况下，PCA并不能得到较好的保留数据信息，且PCA对于主成分的分析判断是影响实验结果的重要因素（不好界定主要信息），另外，PCA对于非线性的数据降维效果较差，后续博客会分析其他算法优化或解决上述问题。