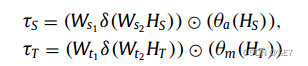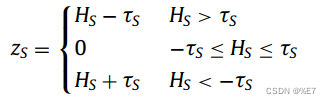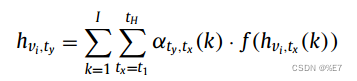本文的主要贡献如下:

（1）设计了一种新颖的端到端交通预测框架，该框架利用注意力机制对时空相关性进行建模。此外，还提出了一种软阈值融合方法来调整空间和时间相关性的流动。

（2）提出了一种多尺度卷积网络，用于捕获不同分辨率的复杂时空特征，提高预测性能。

（3）我们在两个公开的数据集上进行了大量的实验，以验证我们提出的模型在交通预测任务方面的效率。实验结果表明，与现有的基线相比，我们的模型具有更好的预测性能。

时空位置嵌入

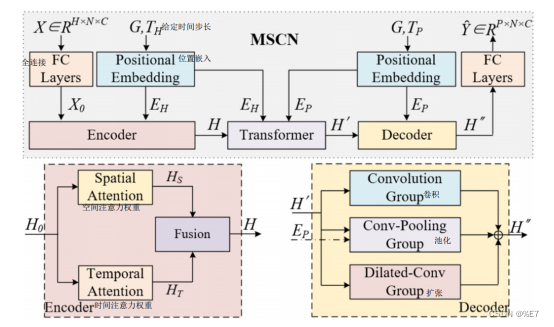
首先，利用两个全连接神经网络提取输入向量的特征;然后，利用先验位置嵌入实现时空嵌入。

然后，在编码器中，一个空间注意和一个时间注意共同编码空间和时间相关性。在编码器之后，变压器注意层用于对历史时间和未来时间之间的时间相关性进行建模。最后，在解码器中，一个卷积层、一个卷积池化层和一个扩展卷积层共同提取复杂的时空特征。

设计了一个时空位置嵌入层来学习嵌入到节点中的特征， 空间嵌入和 和时间嵌入，用邻接矩阵A初始化，用单热编码初始化，H个时间步长内N个节点的嵌入特征表示为，Ft为全连接层，用于将特征转化为d维向量，是未来P个时间步长内N个节点的嵌入特征，然后将他们分别输入编码器和解码器。

具有时空注意的解码器

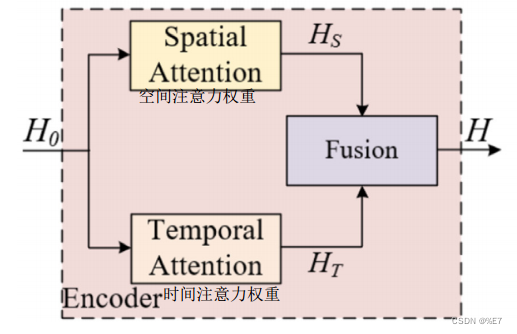
提出了一个基于注意力的编码器。编码器由空间注意、时间注意和软阈值融合三个子组件组成

空间注意：

        类似GMAN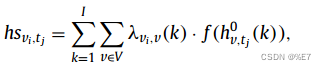，，为隐藏状态，

表示节点v对节点vi在第k个头部的归一化分数，权重和为1，fx为非线性变换W和b为可学习参数，空间注意力输出用表示。

时间注意：

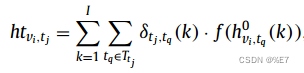
，为节点vi在时间步长tj的隐藏状态，表示归一化时间步长tq在第k个头注意处对时间步长tj的得分。

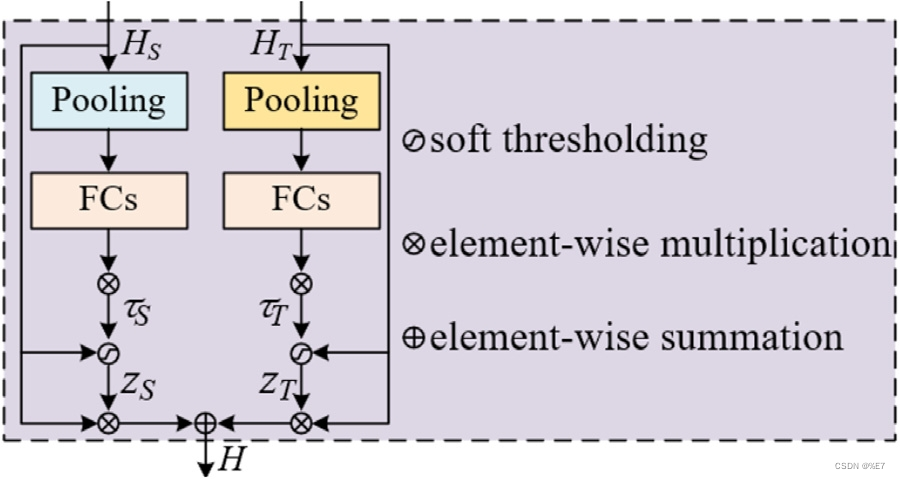
软阈值融合：

        受门控融合和软阈值机制的启发，设计了一种自动关注重要特征而忽略无用特征的软阈值融合。考虑到空间注意和时间注意HS和HT的输出，首先利用全局平均池化(GAP)和全局最大池化(GMP)来最小化过拟合概率。然后将结果送入两个完全连接的层。最后得到空间阈值τS和时间阈值τT，分别表示为

 其中δ为激活函数。表示元素点积。Ws和Wt是可学习的参数。θa、θm分别为GAP操作和GMP操作。以计算空间注意力的软阈值为例，我们有

 因此，HS和HT融合为：

 其中，zS和zT是软阈值，反映了空间和时间相关性的影响程度。软阈值融合机制确保了有用的空间和时间特征得到更多的关注，同时去除了不有用的特征。

 时间步长与注意力转换的相关性

        为了对历史时间步长和未来时间步长之间的相关性进行建模，我们在中使用转换注意力来构建未来表示，然后将其馈送到解码器中。

 其中为节点vi在未来时间步长ty对应的时间相关隐藏状态，为注意力得分，它有助于动态调整编码后的流量特征H。然后将转换注意力的输出H'送入到解码器。

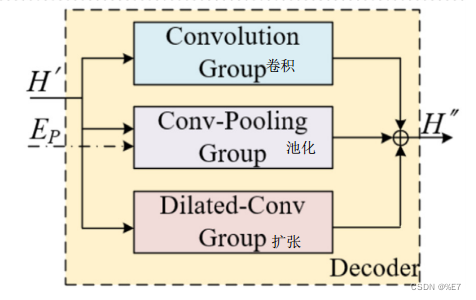
 卷积神经网络解码器

         该解码器由三个卷积层组成:卷积层、卷积池化层和扩展卷积层。针对短期和长期的交通预测，三个卷积层同时处理短序列和超长序列，并发现各种范围的相关性。将这些卷积层的输出连接起来生成最终结果。

Convolution Group：

         观察到一个卷积层只能捕获紧密依赖关系，而一堆卷积层可以捕获任何区域[21]的依赖关系。在卷积群中，我们将Lc卷积叠加如下，其中为卷积层的第i个核参数，为卷积运算。Qc0 = H'为输入，HC = QcLc为输出。为方便起见，过滤器尺寸为3 × 3。

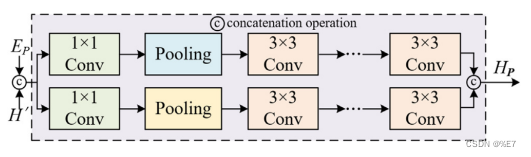
Conv-Pooling Group：

        池化操作对于成功的对流网络至关重要。此外，最大池化操作使广泛的接受域能够提取多尺度流量特征。该模块使用并行结构。一个1 × 1的卷积层，然后是一个最大池化层来计算约简。然后用连续的Lp堆叠3 × 3卷积层提取多尺度特征。卷积化的设计如图所示

Dilated-Conv Group.：

         为了处理长期预测任务，我们应用多尺寸的扩展卷积来处理非常长的序列。研究表明，扩展卷积在处理较长的序列时具有较低的模型复杂度。选择合适的核大小来处理短期和长期预测是一个具有挑战性的问题。1 × 1、3 × 3和5 × 5滤波器尺寸已广泛应用于初始模块，并取得了良好的性能[14]。我们使用3 × 3展开卷积和5 × 5展开卷积的组合来设计模块。单元数为Ld

给定输入H'，输出HC、HP、HD三组，则解码器的最终结果为

其中WC、WP、WD为可学习参数，反映三组的影响程度.

 损失函数

        损失函数的目标是使预测误差最小化。我们使用平均绝对误差(MAE)作为预测值与基本事实之间的损失函数:

 实验结果

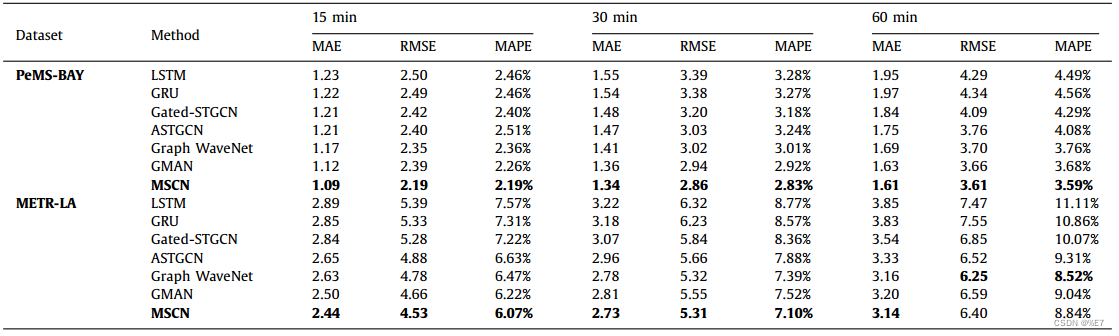
不同交通预测方法的性能比较。

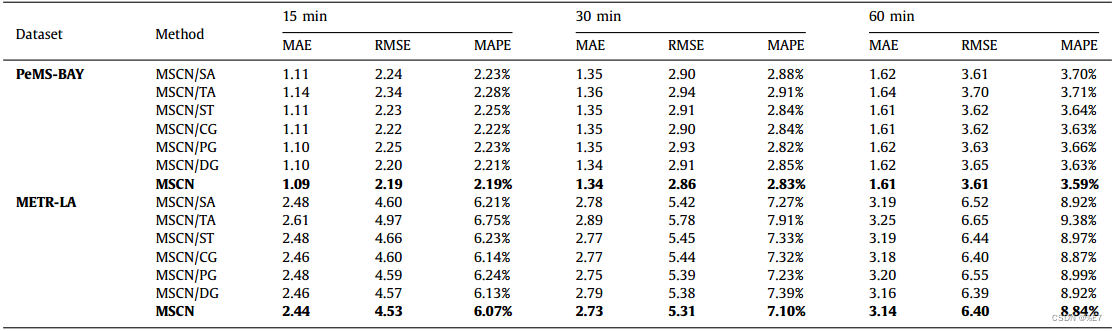
 PeMS-BAY 和 METR-LA的消融分析

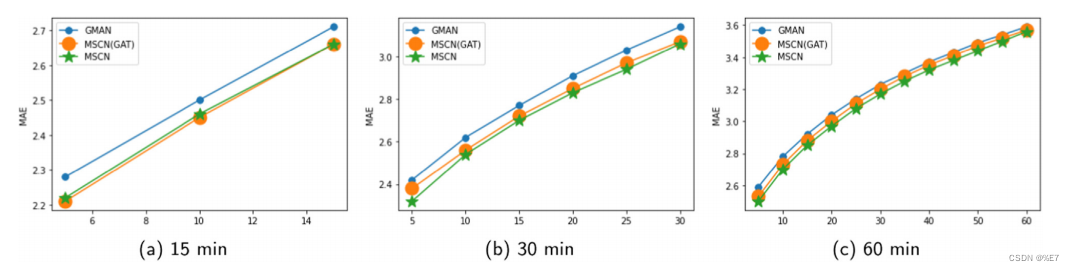
 不同融合方法在METR-LA数据集上的性能比较。

 结论

        本文提出了一种新的时空深度学习网络——多尺度卷积网络(Multi-Scale Convolutional Networks, MSCN)来解决交通流预测问题。MSCN遵循编码器-解码器架构。具体来说，它首先采用了一个图注意网络来精确地模拟时空特征。然后，采用软阈值融合对时空相关流进行调整。最后，推导卷积模块来解码时空序列表示。我们的实验结果表明，MSCN优于最先进的基线。交通状况受许多因素的影响。在未来的工作中，我们将考虑天气、POI等外部因素的影响，进一步提高预测精度。