232. 用栈实现队列

点此跳转题目链接

题目描述

请你仅使用两个栈实现先入先出队列。队列应当支持一般队列支持的所有操作（push、pop、peek、empty）：

实现 MyQueue 类：

• void push(int x) 将元素 x 推到队列的末尾
• int pop() 从队列的开头移除并返回元素
• int peek() 返回队列开头的元素
• boolean empty() 如果队列为空，返回 true ；否则，返回 false

说明：

• 你 只能 使用标准的栈操作 —— 也就是只有 push to top, peek/pop from top, size, 和 is empty 操作是合法的。
• 你所使用的语言也许不支持栈。你可以使用 list 或者 deque（双端队列）来模拟一个栈，只要是标准的栈操作即可。

示例 1：

输入：
["MyQueue", "push", "push", "peek", "pop", "empty"]
[[], [1], [2], [], [], []]
输出：
[null, null, null, 1, 1, false]

解释：
MyQueue myQueue = new MyQueue();
myQueue.push(1); // queue is: [1]
myQueue.push(2); // queue is: [1, 2] (leftmost is front of the queue)
myQueue.peek(); // return 1
myQueue.pop(); // return 1, queue is [2]
myQueue.empty(); // return false

提示：

• 1 <= x <= 9
• 最多调用 100 次 push、pop、peek 和 empty
• 假设所有操作都是有效的 （例如，一个空的队列不会调用 pop 或者 peek 操作）

进阶：

• 你能否实现每个操作均摊时间复杂度为 O(1) 的队列？换句话说，执行 n 个操作的总时间复杂度为 O(n) ，即使其中一个操作可能花费较长时间。

题解

思路很简单：用两个栈来回 “倒” ，像两杯水来回倒那样，就可以模拟队列。

比如用栈 s1 作为实际存储结构，另一个栈 s2 作为辅助结构，要获得“队头”，即 s1 的栈底元素，可以将 s1 中元素依次出栈、入栈 s2 ，这样最后在 s2 栈顶的就是原来 s1 的栈底，即队头元素。

代码（C++）

class MyQueue
{
private:
    stack<int> s1; // 本体
    stack<int> s2;

public:
    MyQueue(){}

    void push(int x)
    {
        s1.push(x);
    }

    int pop()
    {
        // s1倒进s2
        while (!s1.empty()) {
            s2.push(s1.top());
            s1.pop();
        }
        // 出队列
        int top = s2.top();
        s2.pop();
        // s2倒回s1
        while (!s2.empty()) {
            s1.push(s2.top());
            s2.pop();
        }
        return top;
    }

    int peek()
    {
        // s1倒进s2
        while (!s1.empty()) {
            s2.push(s1.top());
            s1.pop();
        }
        // 记录队头元素
        int top = s2.top();
        // s2倒回s1
        while (!s2.empty()) {
            s1.push(s2.top());
            s2.pop();
        }
        // 返回队头元素
        return top;
    }

    bool empty()
    {
        return s1.empty();
    }
};

不过上面这种实现方式在涉及栈顶元素的操作时，总是需要倒两遍（ s1 ➡️ s2 ➡️ s1 ），哪怕连续 peek 也是每次如此，比较麻烦。

我们还可以进一步优化，以达到题目的进阶要求：每个操作均摊时间复杂度为 $O(1)$ 。方法是让两个栈分别负责“入队列”和“出队列”，分开维护：

class MyQueue
{
private:
    stack<int> stIn; 
    stack<int> stOut;

public:
    MyQueue() {}

    void push(int x)
    {
        stIn.push(x);
    }

    int pop()
    {
        // 如果stOut为空，需要先倒入此时的stIn
        if (stOut.empty()) {
            while (!stIn.empty()) {
                stOut.push(stIn.top());
                stIn.pop();
            }
        }
        // 出队列（stOut出栈）并返回队头（stOut栈顶）
        int top = stOut.top();
        stOut.pop();
        return top;
    }

    int peek()
    {
        int top = this->pop(); // 直接复用pop()
        stOut.push(top);       // 记得要加回去
        return top;
    }

    bool empty()
    {
        return stIn.empty() && stOut.empty();
    }
};

Golang中没有现成的栈和队列，所以这里用go也写一下：

这里就直接实现队列了，先实现栈、再用它来实现队列的思路同上。

type MyQueue struct {
	s []int
}


func Constructor() MyQueue {
	return MyQueue{}
}


func (queue *MyQueue) Push(x int)  {
	queue.s = append(queue.s, x)
}


func (queue *MyQueue) Pop() int {
	top := queue.s[0]
	queue.s = queue.s[1:]
	return top
}


func (queue *MyQueue) Peek() int {
	return queue.s[0]
}


func (queue *MyQueue) Empty() bool {
	return len(queue.s) == 0
}

225. 用队列实现栈

点此跳转题目链接

题目描述

请你仅使用两个队列实现一个后入先出（LIFO）的栈，并支持普通栈的全部四种操作（push、top、pop 和 empty）。

实现 MyStack 类：

• void push(int x) 将元素 x 压入栈顶。
• int pop() 移除并返回栈顶元素。
• int top() 返回栈顶元素。
• boolean empty() 如果栈是空的，返回 true ；否则，返回 false 。

注意：

• 你只能使用队列的标准操作 —— 也就是 push to back、peek/pop from front、size 和 is empty 这些操作。
• 你所使用的语言也许不支持队列。 你可以使用 list （列表）或者 deque（双端队列）来模拟一个队列 , 只要是标准的队列操作即可。

示例：

输入：
["MyStack", "push", "push", "top", "pop", "empty"]
[[], [1], [2], [], [], []]
输出：
[null, null, null, 2, 2, false]

解释：
MyStack myStack = new MyStack();
myStack.push(1);
myStack.push(2);
myStack.top(); // 返回 2
myStack.pop(); // 返回 2
myStack.empty(); // 返回 False

提示：

• 1 <= x <= 9
• 最多调用100 次 push、pop、top 和 empty
• 每次调用 pop 和 top 都保证栈不为空

进阶： 你能否仅用一个队列来实现栈。

题解

思路很简单，用两个队列， q1 作为实际存储结构， q2 作为辅助数据结构，涉及栈顶的操作则将 q1 “倒入” q2 并注意留下最后一个元素（即 q1 队尾元素）作为栈顶元素即可。

代码（C++）

class MyStack
{
private: 
    queue<int> q1; // q1是本体
    queue<int> q2;

public:
    MyStack() {}

    void push(int x)
    {
        q1.push(x);
    }

    int pop()
    {
        // q1倒进q2，留意最后一个值
        int size = q1.size();
        for (int i = 0; i < size - 1; i++) {
            q2.push(q1.front());
            q1.pop();
        }
        int top = q1.front();
        q1.pop();
        // q2倒回q1
        while (!q2.empty())
        {
            q1.push(q2.front());
            q2.pop();
        }
        // 返回栈顶
        return top;
    }

    int top()
    {
        int top;
        // q1倒进q2，留意最后一个值
        while (1)
        {
            top = q1.front();
            q2.push(top);
            q1.pop();
            if (q1.empty())
                break;
        }
        // q2倒回q1
        while (!q2.empty())
        {
            q1.push(q2.front());
            q2.pop();
        }
        // 返回栈顶
        return top;
    }

    bool empty()
    {
        return q1.empty();
    }
};

这样思路应该是最简单的，但是实现也比较繁琐，因为需要经常在两个队列之间倒腾元素。我们可以优化一下，达到题目进阶要求中的只用一个队列实现：

由于队列是“先进先出”的数据结构，上面用两个队列的地方其实完全可以仅用一个队列实现：根据情况将其队头元素插到队尾即可

class MyStack
{
private:
    queue<int> q;

public:
    MyStack() {}

    void push(int x)
    {
        q.push(x);
    }

    int pop()
    {
        int size = q.size();
        for (int i = 0; i < size - 1; i++) {
            q.push(q.front());
            q.pop();
        }
        int top = q.front();
        q.pop();
        return top;
    }

    int top()
    {
        int top = this->pop();
        q.push(top);
        return top;
    }

    bool empty()
    {
        return q.empty();
    }
};

Golang中没有现成的栈和队列，所以这里用go也写一下：

这里就直接实现栈了，先实现队列、再用它来实现栈的思路同上。

type MyStack struct {
	slice []int
}


func Constructor() MyStack {
	return MyStack{}
}


func (st *MyStack) Push(x int)  {
	st.slice = append(st.slice, x)
}


func (st *MyStack) Pop() int {
	top := st.slice[len(st.slice) - 1]
	st.slice = st.slice[0 : len(st.slice) - 1]
	return top
}


func (st *MyStack) Top() int {
	top := st.Pop()
	st.slice = append(st.slice, top)
	return top
}


func (st *MyStack) Empty() bool {
	return len(st.slice) == 0
}

20. 有效的括号

点此跳转题目链接

题目描述

给定一个只包括 '('，')'，'{'，'}'，'['，']' 的字符串 s ，判断字符串是否有效。

有效字符串需满足：

1. 左括号必须用相同类型的右括号闭合。
2. 左括号必须以正确的顺序闭合。
3. 每个右括号都有一个对应的相同类型的左括号。

示例 1：

输入：s = "()"
输出：true

示例 2：

输入：s = "()[]{}"
输出：true

示例 3：

输入：s = "(]"
输出：false

提示：

• 1 <= s.length <= 104
• s 仅由括号 '()[]{}' 组成

题解

一道用于理解“栈”的很好题目。思路有点像求逆波兰表达式（应该说这题是逆波兰表达式的基础）：

• 左括号无脑入栈

• 遇到右括号，检查当前栈顶是否为相应的左括号（这就检查了右括号是否顺序闭合），是就弹出左括号，否则返回false

  这里还要注意：先检查栈是否为空

• 其他字符不入栈

• 最后，如果栈为空，说明所有括号都配对正确，返回true；否则，返回false

代码（C++）

bool isValid(string s)
{
    stack<char> st;
    for (const char &c : s){
        switch (c)
        {
        case '(':
        case '[':
        case '{':
            st.push(c);
            break;

        case ')':
            if (st.empty() || st.top() != '(')
                return false;
            else
                st.pop();
            break;

        case ']':
            if (st.empty() || st.top() != '[')
                return false;
            else
                st.pop();
            break;

        case '}':
            if (st.empty() || st.top() != '{')
                return false;
            else
                st.pop();
            break;

        default:
            break;
        }
    }
    return st.empty();
}

这个代码直观但是有点长，浅改一下：

bool isValid(string s)
{
    stack<char> st;
    unordered_map<char, char> cMap = {
        {')', '('},
        {']', '['},
        {'}', '{'}
    };
    for (char c : s)
    {
        if (cMap.find(c) != cMap.end()) {
            if (st.empty() || st.top() != cMap[c])
                return false;
            st.pop();
        } else if (c == '(' || c == '[' || c == '{')
            st.push(c);
    }
    return st.empty();
}

1047. 删除字符串中的所有相邻元素

点此跳转题目链接

题目描述

给出由小写字母组成的字符串 S，重复项删除操作会选择两个相邻且相同的字母，并删除它们。

在 S 上反复执行重复项删除操作，直到无法继续删除。

在完成所有重复项删除操作后返回最终的字符串。答案保证唯一。

示例：

输入："abbaca"
输出："ca"
解释：
例如，在 "abbaca" 中，我们可以删除 "bb" 由于两字母相邻且相同，这是此时唯一可以执行删除操作的重复项。之后我们得到字符串 "aaca"，其中又只有 "aa" 可以执行重复项删除操作，所以最后的字符串为 "ca"。

提示：

1. 1 <= S.length <= 20000
2. S 仅由小写英文字母组成。

题解

这题一看就和 LeetCode 20. 有效的括号 很像，可以采用类似的思路，即将字符逐个入栈，期间检查：若当前字符与栈顶字符相同，就将栈顶字符弹出。最后，将栈中字符重新连成字符串即可。

好像消消乐 👀

代码（C++）

string removeDuplicates(string s)
{
    stack<char> cs;
    for (char c : s) {
        if (!cs.empty()) {
            if (c == cs.top())
                cs.pop();
            else    
                cs.push(c);
        } else 
            cs.push(c);
    }
    string res = "";
    while (!cs.empty()) {
        res = cs.top() + res; // 栈顶元素加入字符串头部
        cs.pop();
    }
    return res;
}

但进一步思考可以发现，其实没必要这样“先加入，再检查，不符合条件就出栈”，而可以“先检查，确定能加再加入”：

string removeDuplicates(string s) {
    stack<char> cs;
    for (char c : s) {
        // 只把满足条件的元素入栈
        if (cs.empty() || c != cs.top())
            cs.push(c);
        else
            cs.pop();
    }
    string res = "";
    while (!cs.empty())
    {
        res = cs.top() + res; // 栈顶元素加入字符串头部
        cs.pop();
    }
    return res;
}

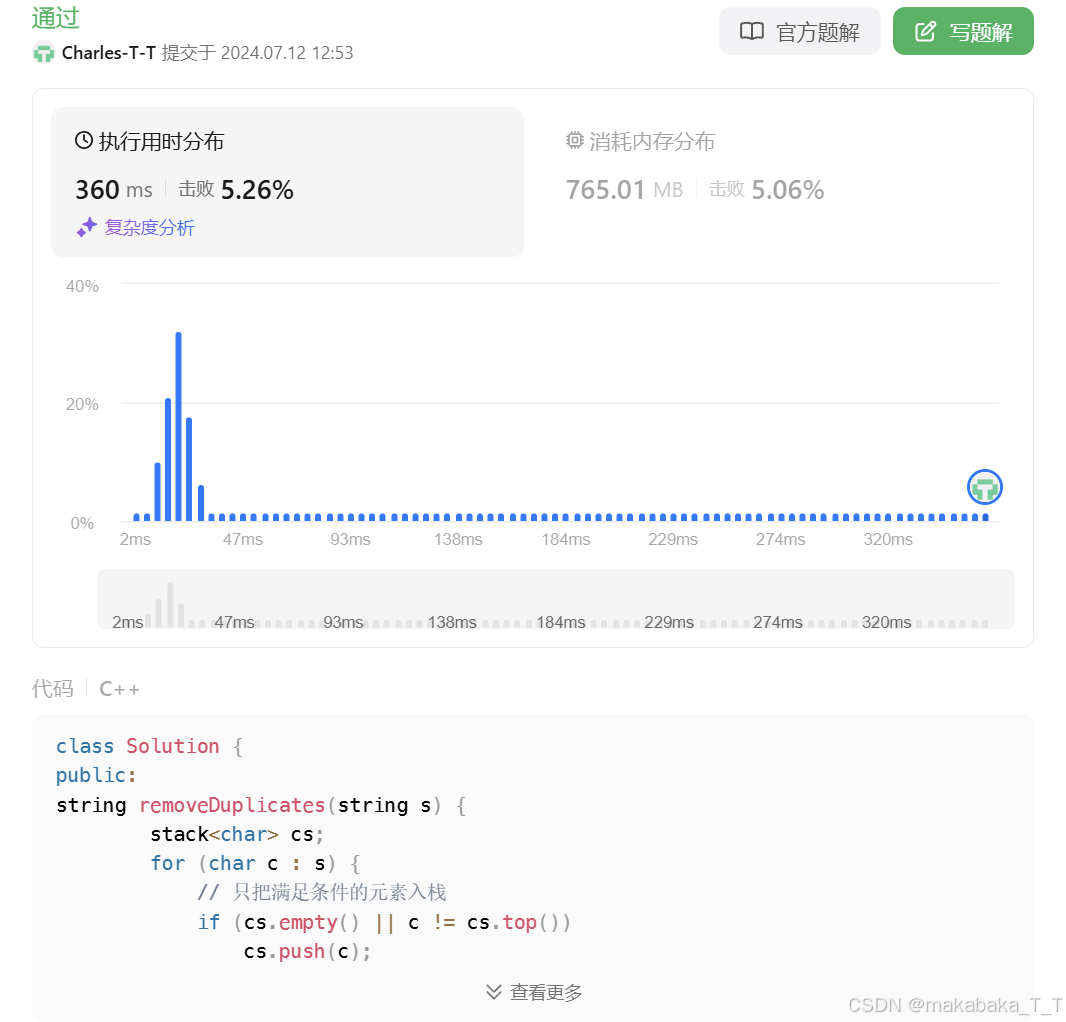
不过这两种方法受栈操作的较低效率限制，速度较慢：

我们可以用 vector 模拟栈，进一步优化实际运行速度：

string removeDuplicates(string s) {
    vector<char> stack;   // 用vector模拟栈
    stack.push_back(' '); // 先加入一个空格，便于统一操作
    for (char c : s) {
        if (c != stack.back())
            stack.push_back(c);
        else
            stack.pop_back();
    }
    return string(stack.begin() + 1, stack.end());
}

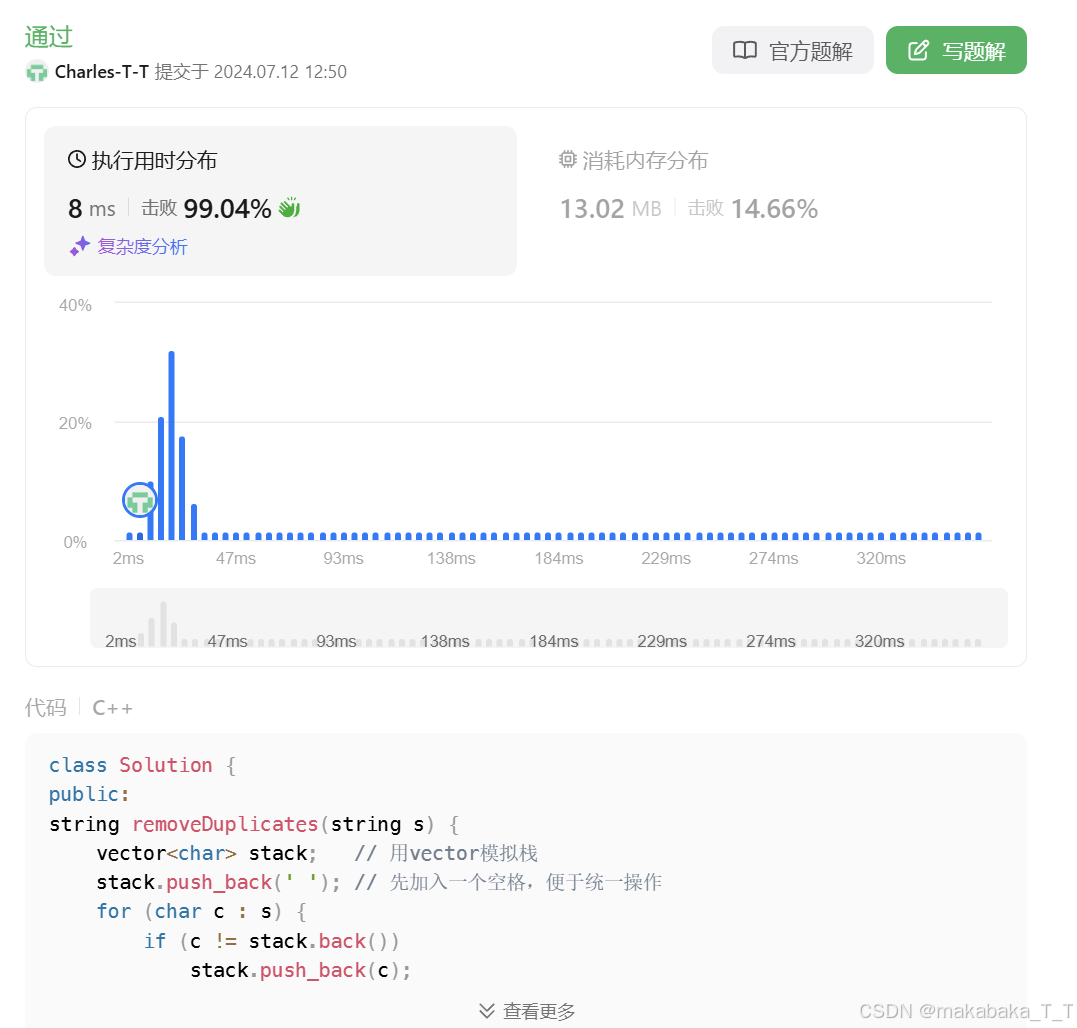
这种写法的时空开销都小不少，LeetCode上看到运行速度明显提升：